Методичні матеріали "Прикладна спрямованість шкільного курсу математики"

Про матеріал

Встановлення зв’язку шкільної математики з життям, доведення того, що прикладні математичні задачі є джерелом міжпредметних асоціацій, засобом формування життєво важливих компетентностей учнів, а їх розв'язування шляхом до реалізації міжпредметних зв’язків математики та інших навчальних дисциплін.

Перегляд файлу

ВІДДІЛ ОСВІТИ, МОЛОДІ ТА СПОРТУ

ШАЦЬКОЇ РАЙОННОЇ ДЕРЖАВНОЇ АДМІНІСТРАЦІЇ

Загальноосвітня школа І-ІІІ ст. с. Піща

ПРИКЛАДНА СПРЯМОВАНІСТЬ

ШКІЛЬНОГО КУРСУ МАТЕМАТИКИ

Матеріали підготувала

Терещук Світлана Іванівна,

вчитель математики

ЗОШ І-ІІІ ст. с, Піща

ЗМІСТ

ВСТУП ……………………………...………………………………………………….... 2

І. ПЕДАГОГІЧНІ АСПЕКТИ ПРИКЛАДНОЇ СПРЯМОВАНОСТІ ШКІЛЬНОГО КУРСУ МАТЕМАТИКИ

1.1. Поняття прикладної спрямованості математики……….…...……. …………….. 4

1.2. Математичне моделювання як засіб реалізації прикладної спрямованості математики…..…………………………………………………………………………….8

1.3.Прикладні задачі як засіб здійснення міжпредметних зв’язків…….……...……..23

1.4. Взаємозв’язок принципу історизму та прикладної спрямованості математики..34

ІІ. ДОБІРКА ПРИКЛАДНИХ ЗАДАЧ

2.1. Алгебраїчні задачі ………………..……………………………………...….………39

2.2. Задачі з геометрії ………………………………………………………….………..51

ВИСНОВКИ ……………………..…………………...……………………..…………..60

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ………………………..…………………..63

ВСТУП

Зближення теорії з практикою дає

найкращі результати, і не лише

одна практика від цього виграє.

П. Л. Чебишев.

На сучасному етапі розвитку нашої держави роль математики в системі шкільної освіти істотно зростає і характеризується новим розумінням цілей навчання та новими підходами до розробки і використання освітніх технологій. Суспільству потрібна компетентна, творча особистість, яка здатна брати активну участь у розвитку сучасного виробництва, економіки, науки та культури. Щоб стати успішним у сучасному складному і мінливому суспільному житті, кожній людині необхідно бути мобільною, адаптивною, вміти не лише бачити проблему, а й чітко формулювати та всебічно підходити до її розв’язування, здобувати необхідну інформацію тощо.

Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності і навичками їх застосувань до розв’язування прикладних задач., тому на думку О. Я. Савченко, школа повинна особливу увагу звертати на ті питання програми, з якими можуть зустрітися її вихованці в житті.

Серед напрямів, що можуть поліпшити рівень загальноосвітньої математичної освіти, є посилення практичного спрямування шкільного курсу математики, що передбачає вироблення в учнів умінь і навичок використовувати здобуті знання в практичній діяльності : математично досліджувати реальні явища, складати математичні моделі для розв’язування задач з різних галузей науки, економіки, виробництва та зіставляти знайдені результати зі справжніми. Крім того практичні вміння і навички з математики необхідні і для майбутньої діяльності школярів при вивченні фізики, хімії, географії, інформатики [7].

У процесі роботи над прикладними задачами, особливо тими, які не втратили своєї актуальності впродовж століть, учні не лише засвоюють найважливіші математичні поняття, але й відчувають зв'язок теорії з практикою, усвідомлюють значення та необхідність вивчення теми, формують ключові компетентності, що забезпечує гармонійну взаємодію із суспільством [24].

Мета роботи: встановлення зв’язку шкільної математики з життям, доведення того, що прикладні математичні задачі є джерелом міжпредметних асоціацій, засобом формування життєво важливих компетентностей учнів, а їх розв'язування шляхом до реалізації міжпредметних зв’язків математики та інших навчальних дисциплін.

Об’єкт дослідження: навчально-виховний процес із застосуванням прикладних задач як на уроках математики, тік і на інших уроках.

Предмет дослідження: використання на уроках математики прикладних задач, як засобу формування наукового світогляду, творчого мислення, активізації пізнавальної діяльності учнів, формування основних прийомів мислення (порівняння, узагальнення, абстрагування, класифікації, аналогії, аналізу, синтезу) і більш складних, що базуються на них (конструювання означень через рід і видові відмінності, виділення головного, побудова індуктивних і дедуктивних висновків, встановлення відношень між поняттями, складання схем, плану, конспекту, перенесення прийомів за аналогією, застосування минулого досвіду.

Гіпотеза дослідження – якщо систематично реалізовувати прикладну спрямованість шкільного курсу математики при вивченні теоретичного матеріалу і розв’язуванні задач, то це посилить мотивацію й ефективність навчання.

Нові суспільні умови та нові завдання освітньої галузі „математика” потребують корекції існуючих шляхів досягнення мети та вирішення зазначеної проблеми шкільного курсу математики. У школі треба раз і назавжди відмовитися від технократичного мислення, коли засоби переважають над метою, коли на учня дивляться як на об’єкт маніпуляцій, який навчають або програмують, а не як на особистість з безліччю ступенів свободи її інтелекту.

І. ПЕДАГОГІЧНІ АСПЕКТИ ПРИКЛАДНОЇ СПРЯМОВАНОСТІ ШКІЛЬНОГО КУРСУ МАТЕМАТИКИ

1.1 Поняття прикладної спрямованості математики.

Існує необхідність так організовувати вивчення математики, щоб воно було корисним і водночас захоплюючим, цікавим. А це можливо шляхом подолання надмірної абстракції, через розкриття ролі математики в пізнанні навколишнього світу, через інтеграцію з іншими шкільними предметами та формування у такий спосіб цілісного, гармонійного світосприйняття дитини.

У методиці навчання математики існують різні тлумачення поняття “прикладна спрямованість”. Ю. М. Налягін і В. В. Пікан, наприклад, розрізняють поняття “прикладна” і “практична” спрямованість. На їх погляд “прикладна спрямованість навчання математики – це орієнтація змісту і методів навчання на застосування математики в техніці і суміжних науках; у професійній діяльності; в народному господарстві і побуті”. Згідно з таким тлумаченням міжпредметні зв’язки, політехнічна спрямованість охоплюються поняттям “прикладна спрямованість”. Вона сприяє формуванню наукового світогляду і показує роль математики в сучасному виробництві, економіці, науці.

Практична спрямованість навчання математики – “це спрямованість змісту і методів навчання на розв’язування задач і вправ, на формування у школярів навичок самостійної діяльності математичного характеру”. У реальному процесі навчання прикладна і практична спрямованість звичайно функціонують спільно.

Дещо інакше розуміємо прикладну спрямованість В.А. Долінгер. Він вважає, що “прикладна спрямованість математичних знань повинна означати як їх практичне застосування, так і їх теоретичне значення в самій математиці. Лише в цьому випадку буде виховуватися в учнів справжня повага до сили наукових знань”.

Державний стандарт базової та повної середньої освіти основними цілями освітньої галузі «Математика» визначає:

опанування учнями системи математичних знань, умінь та навичок, необхідних у повсякденному житті та майбутній професійній діяльності, достатніх для успішного оволодіння на сучасному рівні предметів природничо-наукового та гуманітарного циклів, забезпечення неперервної освіти протягом життя;
формування в учнів наукового світогляду, уявлень про ідеї та методи математики, про її роль у пізнанні дійсності;
інтелектуальний розвиток учнів.

Реалізувати поставлені завдання можна за умови посилення практичної, прикладної та політехнічної спрямованості шкільного курсу математики.

Практичне спрямування передбачає формування в учнів умінь та навичок безпосередньо застосовувати здобуті знання під час вивчення теоретичного курсу математики.

Прикладне спрямування забезпечує вміння учнів використовувати здобуті під час вивчення математики знання в практичній діяльності (дослідженні реальних явищ, складанні математичних моделей задач та зіставленні отриманих результатів з реальними) та при вивченні природничих наук (фізики, біології, географії, астрономії, хімії).

Політехнічна направленість навчання передбачає використання математичних знань і вмінь у розв’язуванні задач, зміст яких пов'язаний із описом виробничих циклів, процесів обслуговування та керування (фізики, хімії, креслення, трудового навчання тощо).

Прикладна спрямованість навчання математики найбільше реалізується при розв’язуванні прикладних задач. Під прикладними задачами в школі здебільшого розуміють задачі, які виникають поза курсом математики і розв’язуються математичними методами і способами, які визначаються в шкільному курсі. У педагогічній літературі поняття прикладної задачі трактується по різному, а саме:

задача, що потребує перекладу з природної мови на математичну;
задача, яка близька за формулюванням і методами розв’язування до задач, що виникають на практиці;
сюжетна задача, сформульована у вигляді задачі-проблеми.

Сформулюємо основні вимоги до прикладних задач, які використовуються у навчанні математики:

задачі повинні мати реальний практичний зміст, який забезпечує ілюстрацію практичної цінності і значущості набутих математичних знань;
задачі повинні відповідати шкільним програмам і підручникам за формулюванням і змістом методів і фактів, які будуть використовувати в процесі їх розв’язування;
задачі повинні бути сформульовані доступною і зрозумілою мовою, не містити термінів, з якими учні не зустрічалися і які вимагатимуть додаткових пояснень;
числові дані в прикладних задачах повинні бути реальними, відповідати існуючим в практиці;
у змісті задачі по можливості повинен бути відображений особистий досвід учнів, місцевий матеріал, який дозволяє ефективно показати використання математичних знань і викликати в учнів пізнавальний інтерес;
прикладні задачі повинні відображати ситуації промислового і сільськогосподарського виробництва, економіки, торгівлі, ілюструвати застосування математичних знань у конкретних професіях людей;
у прикладних задача числові дані, як правило, мають бути наближеними, а при їх розв’язуванні необхідно використовувати обчислювальні засоби, зокрема ЕОМ.
при розв’язанні прикладних задач у класах з поглибленим вивченням математики їх формулювання може бути розширене і являти собою деяке теоретичне зведення до проблеми, що вивчається. Сама проблема може мати багатоступеневе розв’язання, при якому кожний наступний етап розвиває і доповнює попередній [7].

Кожна прикладна задача виконує різні функції, що за певних умов виступають явно або приховано.

Окремі задачі ілюструють зазначений у природи принцип оптимізації трудової діяльності (діставати найбільший ефект з найменшими затратами), інші – розвивають здібності учнів до технічної творчості (геометричні задачі на побудову тощо). Розв’язування прикладних задач сприяє ознайомленню учнів з роботою підприємств і галузей народного господарства, що є умовою орієнтації інтересу учнів до певних професій. Використання прикладних задач дозволяє вдало створювати проблемну ситуацію на уроці. Такі задачі стимулюють учнів до здобуття нових знань, збагачування учнів теоретичними знаннями з технічних та інших дисциплін [10].

Численні науково-методичні публікації свідчать про важливість цього напряму у викладанні математики в школі.

1.2 Математичне моделювання як засіб реалізації прикладної спрямованості математики

У міру свого розвитку більшість наук використовують усе більше доконаний арсенал математики. Можна прийти до висновку, що математика – це «цемент», що зв’язує воєдино науки, бо без логічного апарата математики не обійдеться жодна з них.

Досвід розвитку сучасних наук показує, що на певному етапі розвитку майже всіх наукових дисциплін неминуче відбувається їх математизація, результатом якої є створення логічно струнких формалізованих теорій і подальший прискорений розвиток дисципліни.

У прикладних аспектах гуманітарних наук доцільно використовувати математичні методи. Математичний апарат теорії ймовірностей дає можливість вивчати масові явища в соціології, лінгвістиці. Математичні методи відіграють важливу роль при обробці статистичних даних, моделюванні.

Моделювання - метод наукового пізнання, що грунтується на вивченні реальних об'єктів за допомогою вивчення моделей цих об'єктів, що є більш доступними для дослідження і володіють властивостями реальних об'єктів.

Математичне моделювання широко використовується там, де експериментальні дослідження трудомісткі і дорогі, або взагалі неможливі (наприклад, у вивченні соціальних явищ). Крім завдання прогнозу, математичне моделювання допомагає класифікувати і систематизувати фактичний матеріал, побачити існуючі зв'язки в мозаїці фактів. Це випливає з того, що модель є специфічно-яскравою і виразною мовою, призначеною для опису досліджуваного об'єкта або явища.

Математична модель – наближений опис якого-небудь класу явищ зовнішнього світу, виражений за допомогою математичної символіки. Аналіз математичної моделі дозволяє проникнути в сутність досліджуваних явищ. Математична модель – могутній метод пізнання зовнішнього світу, а також прогнозування і керування. Процес математичного моделювання, тобто вивчення явища за допомогою математичної моделі, можна поділити на чотири етапи.

Перший етап – формулювання законів, що пов'язують основні об'єкти моделі. Цей етап вимагає широкого знання фактів, що стосуються досліджуваних явищ, і глибокого розуміння їхнього взаємозв'язку. Ця стадія завершується записом сформульованих якісних уявлень про зв'язки між об'єктами моделі у математичних термінах.

Другий етап – дослідження математичних задач, до яких приводять математичні моделі. Основним питанням тут є розв'язання прямої задачі, тобто одержання в результаті аналізу моделі вихідних даних (теоретичних висновків) для подальшого зіставлення їх з результатами спостережень досліджуваних явищ. На цьому етапі важливу роль набувають математичний апарат, необхідний для аналізу математичної моделі, і обчислювальна техніка – могутній засіб для одержання кількісної вихідної інформації як результату розв'язування складних математичних задач. Часто математичні задачі, що виникають на основі математичної моделі різних явищ, бувають однаковими (наприклад, основна задача лінійного програмування відображає ситуації різної природи). Це дає підставу розглядати такі типові математичні задачі як самостійний об'єкт, абстрагуючись від досліджуваних явищ.

Третій етап – з'ясування того, чи задовольняє прийнята гіпотетична модель критерії практики, тобто з'ясування питання про те, чи узгоджуються результати спостережень з теоретичними висновками моделі в межах точності спостережень. Якщо модель була цілком визначена (усі параметри її були задані), то визначення відхилень теоретичних висновків від спостережень дає розв'язання прямої задачі з наступною оцінкою відхилень. Якщо відхилення виходять за межі точності спостережень, то модель не можна прийняти. Часто в процесі побудови моделі деякі її характеристики залишаються не визначеними. Задачі, у яких визначаються характеристики моделі (параметричні, функціональні) так, щоб вихідну інформацію можна було порівняти в межах точності спостережень з результатами спостережень досліджуваних явищ, називаються оберненими задачами. Якщо математична модель така, що ні при якому виборі характеристик ці умови не можна задовольнити, то модель непридатна для дослідження розглянутих явищ. Застосування критерію практики до оцінки математичної моделі дозволяє робити висновок про правильність положень, які лежать в основі моделі (гіпотетичної), що підлягає вивченню. Цей метод є єдиним методом вивчення недоступних нам безпосередньо явищ макро- і мікросвіту.

Четвертий етап – наступний аналіз моделі в зв'язку з нагромадженням даних про досліджувані явища і модернізація моделі. У процесі розвитку науки і техніки дані про досліджувані явища усе більше і більше уточнюються і настає момент, коли висновки, що одержують на основі існуючої математичної моделі, не відповідають нашим знанням про явище. Таким чином, виникає необхідність побудови нової, досконалішої математичної моделі. Типовим прикладом, що ілюструє характерні етапи побудови математичної моделі, є модель Сонячної системи. Спостереження зоряного неба почалися в далеку давнину. Первинний аналіз цих спостережень дозволив виділити планети з усього різноманіття небесних світил. Таким чином, першим кроком було виділення об'єктів вивчення. Другим кроком стало визначення закономірностей їхніх рухів. (Узагалі визначення об'єктів і їх взаємозв'язків є вихідними положеннями – «аксіомами» – гіпотетичної моделі.) Моделі Сонячної системи в процесі свого розвитку пройшли через ряд послідовних удосконалень. Першою була модель Птолемея (2 ст. н.е.), яка виходила з положення, що планети і Сонце рухаються навколо Землі (геоцентрична модель), і описувала ці рухи за допомогою правил (формул), що багаторазово ускладнювалися в процесі нагромадження спостережень. Розвиток мореплавання поставив перед астрономією нові вимоги до точності спостережень. М. Коперник у 1543 р. запропонував принципово нову основу законів руху планет, яка базувалася на тому, що планети обертаються навколо Сонця по колу (геліоцентрична система). Це була якісно нова (але не математична) модель Сонячної системи. Однак не існувало параметрів системи (радіусів кіл і кутових швидкостей руху), що приводять кількісні висновки теорії в належну відповідність зі спостереженнями. Таким чином М. Коперник був змушений ввести виправлення в рухи планет по колу (епіцикли).

Наступним кроком у розвитку математичної моделі Сонячної системи були дослідження Й. Кеплера (початок 17 ст.), який сформулював закони руху планет. Положення М. Коперника та Й. Кеплера давали кінематичний опис руху кожної планети окремо, не враховуючи причин, що обумовлюють ці рухи. Принципово новим кроком були роботи І.Ньютона, що запропонував у другій половині 17 ст. динамічну модель Сонячної системи, яка базувалася на законі всесвітнього тяжіння. Динамічна модель узгоджується з кінематичною моделлю, запропонованою Й. Кеплером, оскільки з динамічної системи двох тіл «Сонце – планета» випливають закони Кеплера.

До 40-х рр. 19 ст. висновки динамічної моделі, об'єктами якої були видимі планети, ввійшли в суперечність з накопиченими на той час спостереженнями.

Рух Урана, що спостерігався, ухилявся від теоретично обчисленого руху. У. Левер'є в 1846 р. доповнив систему планет, що спостерігаються, новою гіпотетичною планетою, яку назвав Нептуном, і, користуючись новою математичною моделлю Сонячної системи, визначив масу і закон руху нової планети так, що у новій системі суперечності щодо руху Урана було знято. Планету Нептун було відкрито в місці, визначеному У. Левер'є.

Аналогічним методом, використовуючи розбіжності в теоретичній траєкторії Нептуна і траєкторії, що спостерігалася, у 1930 р. було відкрито планету Плутон.

Метод математичного моделювання, що зводить дослідження явищ зовнішнього світу до математичних задач, займає провідне місце серед інших методів дослідження, особливо в зв'язку з появою ЕОМ.

Він дає змогу проектувати нові технічні засоби, що працюють в оптимальних режимах, для розв'язування складних задач науки і техніки; проектувати нові явища.

Математичні моделі виявили себе як важливий засіб керування. Вони застосовуються в різних галузях знань, стали необхідним апаратом в економічному плануванні та є важливим елементом автоматизованих систем керування.

В педагогічних дослідженнях значно простіше. Прикладну спрямованість математики розуміють як змістовний та методологічний зв’язок шкільного курсу з практикою, що обумовлює формування в учнів навичок, необхідних для розв’язування засобами математики практичних задач. А оскільки в основі їх розвитку лежить також математичне моделювання, то для реалізації прикладної спрямованості необхідно організувати навчання елементам моделювання, що з дидактичної точки зору є навчальними діями, які виконуються в процесі виконання задач.

Моделювання як спосіб пізнання та дослідження застосовується у шкільному навчанні вже у 1 класі при вивченні предметів природничого циклу, праці, творчості. З переходом учнів до основної школи настає час ознайомити їх з математичним моделюванням як прийомом діяльності при дослідженні реальних об’єктів і процесів та при розв’язуванні задач прикладного характеру.

Першими кроками є прищеплення учням навичок математичного моделювання, правильного виконання всіх його етапів. Та найперше слід прикласти всі сили, щоб учні усвідомили поняття «математична модель», адже найбільш відповідальним і складним етапом розв'язування прикладної задачі є побудова її математичної моделі. Тому навіть при розв'язуванні простих задач інколи слід використовувати математичне моделювання, щоб підготувати учнів до розв'язування більш складних завдань.

Слово «модель» утворилося від латинського слова, що означає «міра», «образ», «засіб». Ми використовуємо модель як образ (зразок) чогось, за її допомогою ми маємо можливість щось досліджувати. Моделювання можна розуміти як «створення образа» і його «дослідження», «вивчення». З моделями ми зустрічаємося на кожному кроці: фотографія людини – це її модель, глобус – це модель Землі, іграшки, що оточують дитину, – теж моделі чогось. Це приклади «фізичних» моделей.

Створення моделей та їх дослідження засобами математики називається математичним моделюванням. Чотириста років тому Галілео Галілей стверджував, що «книга природи написана мовою математики». Математичне моделювання використовується як один із самих зручних і ефективних засобів дослідження природи, світу, що оточує нас. За допомогою математики можна створити модель і окремого матеріального об'єкта (наприклад, колеса автомобіля), і складного економічного чи соціального процесу (наприклад, процесу впливу кредитної політики Національного банку на економічну ситуацію в країні), і навіть таких неймовірно далеких від нас природних процесів, як народження і загибель зірок у далеких галактиках.

Звичайно, задачі, що виникають у життєвих ситуаціях і стосуються реальних об'єктів або процесів, тобто прикладні задачі, вимагають переформулювання їх мовою математики. Таке переформулювання називається математичним моделюванням і, відповідно, постановка прикладної задачі в математичних термінах - математичною моделлю цієї задачі.

Реалізація цього етапу вимагає від учнів багатьох умінь: виділяти істотні фактори, що визначають досліджуване явище (процес); вибирати математичний апарат для побудови моделі; виділяти фактори, що викликають похибку при побудові моделі. Прикладні задачі можна умовно розділити на такі, у яких математична модель міститься в умові задачі, та такі, розв'язування яких передбачає побудову математичної моделі.

Процес математичного моделювання складається з трьох етапів: 1) формалізації, переведення запропонованої задачі з звичайної мови на мову математичних термінів тобто побудова математичної моделі задачі; 2) розв’язування задачі усередині моделі (розв’язання отриманої математичної задачі); 3) інтерпретація одержаного розв’язку, тобто переведення одержаного результату (математичного розв’язування) на мову, на якій була сформульована дана задача.

Обов’язковою умовою можливості перенесення інформації з моделі на об’єкт є наявність геометричної, фізичної та математичної подібності. Це перенесення має достатню велику степінь ймовірності. Наприклад, коли кажуть, що площа деякої ділянки землі 20 га, то нехтують тим, що реальна ділянка має невеликі впадини та узгір’я, та визначають його площу множенням довжини на ширину так, нібито ця ділянка зовсім плоска, тобто замінюють реальну поверхню з складною формою ділянки площею плоского прямокутника. При розв’язуванні задачі: «Скільки ходок повинна зробити машина вантажопідйомністю 5 т, щоб вивезти 23 т піску», математичною моделлю задачі буде найменше натуральне число, що дорівнює або більше частки від ділення числа 23 на число 5.

Дуже часто, розв'язуючи прикладні задачі на уроках математики, ми не замислюємося над послідовністю етапів, «змішуємо» їхнє виконання, а кожен з них має свої особливості і вимагає уваги. Розглянемо таку задачу : «У фермера є дві однакові за врожайністю ділянки землі у формі квадратів, причому сторона одного з них у 1,5 рази більша, ніж іншого. У скільки разів урожай з більшого поля перевищує врожай з меншого?». Найперше переведемо цю задачу на мову математики. Йдеться про дві ділянки землі у формі квадратів, тобто за математичну модель кожного поля можна взяти квадрат. Нехай у меншого квадрата сторона дорівнює а, тоді в більшого квадрата сторона дорівнює 1,5 а.

За умовою, врожайність на цих двох полях однакова. Тоді, щоб дізнатися, у скільки разів урожай на другому полі більший від врожаю на першому полі, необхідно обчислити, у скільки разів площа другого поля більша за площу першого поля. Отже, наша задача зводиться до такої математичної задачі: визначити, у скільки разів площа квадрата зі стороною 1,5 а більша за площу квадрата зі стороною а.

Розв'яжемо цю математичну задачу. Площа першого квадрата зі стороною а дорівнює а². Площу другого квадрата зі стороною 1,5 а можна знайти як (1,5 а)² = 2,25 а². Отже, виходить, що площа другого квадрата в 2,25 рази більша за площу першого квадрата.

Ми розв'язали математичну задачу й отримали результат: площа другого квадрата більша від площі першого в 2,25 рази. Звернемося знову до первісної задачі з полями. Перший квадрат – це математична модель першого поля, другий квадрат – математична модель другого поля. Отже, площа більшого поля в 2,25 рази перевищує площу меншого поля. Відповідно, при однаковій урожайності врожай, який фермер збере на другому полі, буде в 2,25 рази більший, ніж на першому.

Звичайно, у житті на розрахунок планованого врожаю впливають ще й такі фактори, як погодні умови, втрати при зборі врожаю і багато інших. У нашій задачі ми припускали, що ці умови, як і врожайність, для двох полів однакові, проте у реальності так буває не завжди. Більш досконала математична модель повинна враховувати всі ці фактори. Такі складні моделі існують, і їх використовують у сучасних господарствах. А ми просто на прикладі цієї простої задачі показати, з яких трьох етапів складається математичне моделювання будь-якого процесу.

При складанні математичної моделі прикладної задачі виникає необхідність створення математичних моделей реальних об'єктів, про які йдеться в задачі. Така об'єкта або процесу може бути представлена у вигляді формули, таблиці, діаграми, геометричної фігури, пропорції тощо. Яка з форм представлення математичної моделі доцільна для розв'язування тієї чи іншої задачі, залежить від самої задачі (тобто від цілей дослідження конкретного об'єкта або процесу).

Значну роль при створенні математичної моделі відіграє виявлення елементів математичного моделювання. В. А. Стукалов виділяє такі елементи: заміна вихідних термінів вибраними математичними еквівалентами; оцінка повноти вихідної інформації та введення при необхідності числових даних, яких не вистачає; вибір точності числових значень, які відповідають змісту задачі; виявлення можливості одержання даних для розв’язуванні задач на практиці.

При математичному моделюванні відсторонюються від якісної різнорідності моделі та об’єкта, від належності їх до різних форм руху матерії. Це узагальнення приймає форму теорії ізоморфізму систем, що набуває характеру математичної подібності. Суть цієї подібності пояснюється тотожністю математичної форми законів природи, що конкретно виражається: фізичні закони математично подібних систем різні, але математична форма їх прояву одна і та ж. Наприклад, система рівнянь з точки зору інженера-електрика може означати рівняння напруги або струму в електричному ланцюгу з активним опором; з точки зору інженера-плановика - рівняння для розрахунку загрузки станків; інженера-будівельника - рівняння, яке з’єднує сили і деформації якоїсь конструкції; інженера-механіка - рівняння рівноваги сил системи ричагів або пружин, а математик скаже: «Це система двох лінійних рівнянь з двома невідомими». Це означає, що математична модель розглядає не об’єкти в їх конкретному вигляді, а структуру відношень, в яких вони виступають.

Інколи поняття, які на перший погляд здаються абстрактними, виражають нерідко не пов’язані між собою закономірності реального світу.

Так, наприклад, лінійна функції у=kx+b може описувати залежність між довжиною стержня та температурою нагрівання: l=l0(1+at); між об’ємом газу та його температурою при сталому тиску: V=V0(1+at) (закон Гей-Люссака); тиском та температурою газу при сталому об’ємі: p=p0(1+bt) (закон Шарля); швидкістю та часом в рівноприскореному русі: v=v0+at і т.д. Тому доцільно розповісти учням, що в курсі фізики кожна з названих залежностей та їх властивості розглядаються самостійно, оскільки фізика має своєрідне відображення реальної дійсності (кожна із закономірностей виводиться з експерименту), в математиці відповідні закономірності та їх властивості вивчаються одночасно.

При вивченні функції у=ax² можна привести приклади залежності шляху від часу при рівноприскореному русі S=at²/2, формулу потужності електричного струму P=l²R при сталому опору та інші формули, які пов’язують різні фізичні величини.

Широту відображення матеріального світу математикою також можна розкрити при вивченні курсу геометрії. Наприклад, в означення поняття “циліндр” входять властивості нескінченної множини предметів, які нас оточують і мають форму циліндра. Розкривши зміст даного поняття, знаходимо властивості його елементів та залежності між ними, застосовуючи їх для кожного предмета, який має форму циліндра. Наприклад, з'ясувавши, що об’єм циліндра V дорівнює добутку площі основи S на висоту h, дізнаємося, як знайти об’єм будь-якого предмету циліндричної форми. На практичних заняттях слід запропонувати учням обчислити об’єми деталей, заготовок, предметів домашнього побуту, які мають форму циліндра (незалежно від кольору, матеріалу), за однією і тією формулою V=S_оснh.

Заслуговує уваги в цьому плані і властивість піраміди: при перетині піраміди площиною, яка паралельна основі, одержуємо переріз, площа якого прямо пропорційна квадрату його відстані від вершини. Ця обставина є теоретичним поясненням залежності між яскравістю поверхні, що світиться, та відстанню від джерела світла. Дійсно, якщо уявити собі, що в вершині піраміди знаходиться джерело світла, то світловий потік, який перехвачується паралельними перерізами піраміди, розподіляється по її поверхні. При віддаленні площадки від вершини на відстань, вдвічі більшу, площа її збільшується в чотири рази, а сила світла, яка приходиться на одиницю площі, стає в чотири рази меншою. Отже, освітленість поверхні, що освітлюється, обернено пропорційна квадрату відстані від її джерела світла.

Користуючись цим законом, сучасна астрономія визначила відстань до найвіддаленіших об’єктів Всесвіту – позагалактичних туманностей, до яких промінь світла доходить за багато сотень тисячоліть.

Необхідно також звернути увагу на предмети, що мають форму найпростіших геометричних фігур, та на їх важливі властивості: рівномірну кривизну круга, “жорсткість” трикутника, осьову та центральну симетрію прямокутника та інше. Дуже добре, коли ці властивості сприймаються учнями конкретно, знаходять підтвердження на практиці. Для того, щоб одержати переконливі відповіді на питання: ”Чому колеса роблять круглими, а стропила даху в вигляді трикутника? Чому зошити та книги мають форму прямокутника?”, достатньо спробувати зробити колесо не круглим, побудувати модель стропил в вигляді чотирикутника або спробувати зробити зошит з листка трикутної форми.

Природа також вирішує проблему оптимізації. Виявляється, що форма шестигранних чарунок у бджолиних стільниках обрана не випадково. Саме завдяки їй бджоли досягають найбільшої місткості стільників при найменших витратах „будівельного матеріалу”.

Дослідженням природи бджолиного стільника займалося багато вчених різних часів. З усіх правильних многокутників тільки трикутниками, квадратами і шестикутниками можна заповнити площину без пропусків та накладань. Тому бджоли повинні були „вибрати” одну з цих фігур. Порівнюючи периметри цих многокутників, запишемо Р₃ : Р₄ : Р₆ ≈ 4,6 : 4 : 3,7.

Отже, бджоли, не вивчаючи математику, вірно„визначили”, що правильний шестикутник має найменший периметр серед фігур рівної площі.

Таким чином, знайомлячи учнів на уроках математики з абстрактними поняттями, необхідно показати їм конкретні об’єкти і співвідношення їх один з одним: плоска поверхня стола, класної дошки, дзеркала і крива поверхня м’яча, електричної лампи; туго натягнута нитка та нитка, що закріплена в двох точках і вільно висить та інше. Крім того варто зауважити, що кинутий камінь, випущене ядро летять по параболі, планети Сонячної системи рухаються по еліпсах, а орбіту, найближчу до кола, має Венера, більярдна кулька відскакує від борту під тим самим кутом, під яким вона об нього вдаряється, тощо. Такі співвідношення допомагають встановити причинно-наслідкові зв’язки явищ які вивчаються.

Також можна дати поняття і про деякі співвідношення між геометричними образами (поняття паралельності, перпендикулярності, рівності, подібності, симетрії). Виховання в учнів звички бачити геометричні фігури в навколишніх предметах має дуже важливе значення, оскільки в результаті діти вчаться знаходити залежності між геометрією та практичною діяльністю людей, визначають джерела розвитку наукового знання.

Особливе місце займає в курсі геометрії перетворення, зокрема паралельне перенесення, при вивченні якого необхідно нагадати учням про поступальний рух в фізиці. Наприклад, переміщення повзунка, який рухається в прямолінійних пазах. За допомогою властивостей паралельного перенесення можна розв’язувати значну кількість практичних задач.

Вивчаючи чотирикутник, доречно вказати на одну цікаву властивість, що має практичне значення: рівними чотирикутниками довільної форми можна повністю покрити площину (тобто можна зробити паркет, плитки якого будуть рівними між собою чотирикутниками). Прикладом застосування цієї властивості може бути задача: Визначити, скільки кахлі в розміром 32х32 см необхідно купити для того, щоб викласти на стіну розмірами 1,8х2,4 м.

Для розв'язування цієї задачі реальний об'єкт – кахлі – заміняємо його математичною моделлю – квадратом з довжиною сторони 0,32 м, а математичною моделлю стіни може слугувати прямокутник довжиною 2,4 м і шириною 1,8 м. Математична задача в цьому випадку має такий вигляд: Якою найменшою кількістю квадратів з довжиною сторони 0,32 м можна цілком покрити прямокутник довжиною 2,4 м і шириною 1,8 м?

У підсумок теми «Многокутники» можна знову ж таки повернутися до властивості чотирикутників покривати площину, зокрема викладання паркету чи бруківки на певній площині. Цікавим є той факт, що зробити паркет можна не лише із рівних між собою чотирикутників чи трикутників, а навіть із опуклих і не опуклих чотирикутників.

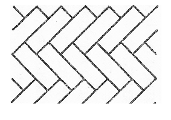
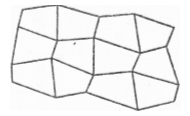
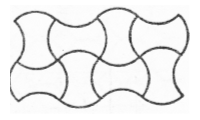
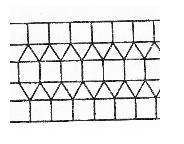
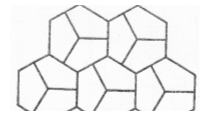У випадку п’ятикутників забруківка можлива не завжди. Так правильними п’ятикутниками забрукувати площину неможливо. Можна лише однаковими неправильними:

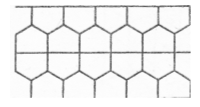
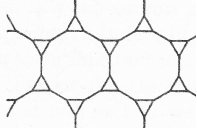
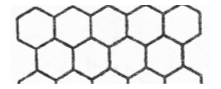Правильними шестикутниками можна забрукувати площину так, як це роблять бджоли в своїх стільниках. Коли ж одночасно змінювати тим же чином шестикутники, то можна одержати вельми цікаві паркети.

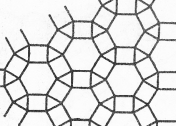
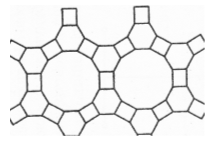
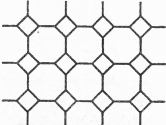Якщо розглядати паркети з багатокутників з великим числом сторін, то слід зауважити, що там уже немає паркетів з правильних багатокутників. Але звернімося ще до паркетів, до яких входять лише правильні багатокутники. В комбінації вони можуть створювати досить оригінальні композиції

Властивості вписаних кутів знаходять застосування при визначенні положення точки за відомим її напрямком на три інші точки, положення яких уже дано. Розв’язування цієї математичної задачі дає змогу визначити, наприклад, положення корабля на морі або літака в повітрі за допомогою радіолокації. Радіостанції (так звані радіомаяки) посилають сигнали визначеної довжини хвилі. Приймальний пристрій на кораблі (рамочна антена) дає можливість визначити напрямок на передавальну радіостанцію. Якщо відомі положення трьох таких маяків і напрямок на них, то існує можливість визначити положення корабля [25].

Перші уроки стереометрії, як правило, складні бо перехід від плоских (двохмірних) образів до просторових (тримірних) потребує великої роботи уявлення. Тому увесь час необхідно звертатися до реальних образів оточуючого світу, а також до моделювання.

Своєрідність відображення дійсності математикою не можна розуміти вузько, тільки як звернення безпосередньо до речей оточуючої нас дійсності і відношенням між ними. Широті розуміння можуть допомогти різного виду моделі, креслення – всі матеріальні реалізації, а також ідеальні образи, зв’язок яких з дійсністю вже зрозумілий учням. Тому учні повинні оволодіти вмінням будувати точні, наочні креслення, вміти їх читати та розуміти, а в простих випадках за кресленням представляти відповідні просторові фігури, адже не випадково кажуть, що креслення – мова техніки.

Математична модель реального об'єкта або процесу може бути представлена у вигляді формули, таблиці, діаграми, геометричної фігури, пропорції тощо. Яка з форм представлення математичної моделі доцільна для розв'язування тієї чи іншої задачі, залежить від самої задачі (тобто від цілей дослідження конкретного об'єкта або процесу).

Реалізація у шкільному курсі математики основної школи окремої змістової лінії «математичне моделювання» без приниження базової теоретичної підготовки учнів допоможе навчати учнів застосуванню знань з математики. Математичне моделювання як елемент математичної грамотності виступає засобом реалізації прикладної спрямованості навчання математики, посилює та збагачує фундаментальну математичну освіту в межах, що відведені основною школою.

Не буде перебільшенням стверджувати, що наявність у шкільній математичній освіті такого прийому діяльності, як математичне моделювання, є ознакою сучасного підходу в навчанні математики, проявом якісної функціональної математичної підготовки учнів.

Серед сучасних математичних методів наукового дослідження найбільшого поширення набув метод математичного моделювання. Він використовується також як метод навчального пізнання у вищій і в загальноосвітній школі.

Фундаторами сучасної методології математичного моделювання були В. М. Глушков, В.Б. Гнеденко, А. М. Колмогоров, О. А. Самарський, А. М. Тихонов, А. Ф. Турбін, В. С. Королюк, В. М. Остапенко та інші. Не дивно, що названі вчені, розробляючи методи математичного моделювання і їх використання в різних галузях науки і техніки, ще в 70-х – 80-х роках прийшли до думки про необхідність навчання математичного моделювання не лише студентів університетів, а й учнів загальноосвітньої школи.

А.М. Колмогоров, розглядаючи питання про сучасну математику та навчання її в школі, підкреслював: «Дивлячись у майбутнє, необхідно вже зараз будувати шкільний курс так, щоб учні були підготовлені до сприйняття нових аспектів прикладної математики.... Задача полягає в тому, щоб уже в школі переконливо показати, що «сучасна математика» дає змогу будувати математичні моделі реальних ситуацій і процесів, що вивчаються в застосуваннях, не тільки не гірше, але логічно послідовніше і простіше, ніж традиційна» [14].

Видатні вчені до прикладної математики відносили ту частину математики, в якій вивчаються математичні структури, які моделюють ті чи інші реальні явища, тобто прикладна математика є наукою, що вивчає реальні явища математичними методами.

На сучасному етапі розвитку шкільної математичної освіти, в умовах особистісно орієнтованого навчання, рівневої та профільної диференціації, проблема навчання майбутніх учителів математики математичного моделювання, навичкам і вмінням такої роботи з учнями середньої школи набула особливої гостроти.

Формування вмінь математичного моделювання, перерахованих у галузевих стандартах – спільна задача всіх математичних курсів, яка в рамках кожної математичної дисципліни може мати свої ефективні та специфічні шляхи реалізації.

Ці шляхи відповідно до концепції базової математичної освіти в Україні, Державних стандартів освіти також знайшли своє відображення у нових програмах математичних курсів та побудованих на їх основі робочих програмах викладачів.

1.3. Прикладні задачі як засіб здійснення між предметних зв’язків.

Математика є одним із опорних предметів загальноосвітньої школи, які забезпечують вивчення різних дисциплін. Математика розповсюджується, завойовуючи все нові й нові області знань, інтенсивно проникає в потаємні куточки наук, допомагає розв'язувати навіть ті задачі, які раніш здавалися недосяжними.

Використання прикладних задач є одним із шляхів реалізації міжпредметних зв'язків - дидактичного принципу організації навчально-пізнавальної діяльності особистості, що сприяє інтеграції математичних та спеціальних дисциплін. Дослідження проблеми інтеграції знань є актуальною темою в методиці навчання різноманітних дисциплін. Навчальні предмети будуються за логікою тієї чи іншої науки, вони не можуть бути ізольовані один від одного. В цьому проявляється основна необхідність принципу інтеграції знань [15].

Міжпредметні зв'язки - це дидактична умова, яка сприяє підвищенню науковості та посильності навчання, значному посиленню пізнавальної діяльності учнів, поліпшенню якості їх знань. Це така конструкція змісту навчального матеріалу, що належить двом чи більше навчальним предметам і відображає взаємозв'язки, які об'єктивно діють в природі та вивчаються сучасними науками. Це свого роду узгодженість між навчальними предметами, що дає змогу розглядати факти і явища реальної дійсності з різних точок зору, з позицій різних навчальних предметів.

Сукупність знань з різних навчальних предметів розкриває зв'язки, що виявляються в дійсності. Нерідко одні й ті самі факти, явища різні науки вивчають з різних точок зору, в різних аспектах. Пізнання цих зв'язків важливе для формування наукового світогляду школярів.

Основними рисами міжпредметних зв'язків є:

1) смислове співвіднесення елементів змісту (об'єктів зв'язку), що входять до складу двох чи більше навчальних предметів (склад зв'язку);

2) методичні прийоми навчання та форми навчального процесу, адекватні предметам, між якими встановлюється зв'язок (спосіб зв'язку);

3) забезпечення цілеспрямованого формування вмінь і навичок комплексного використання знань в процесі розв'язання навчальних задач (направленість зв'язку).

Стосовно процесу навчання міжпредметні зв'язки виступають як дидактичні умови, що сприяють підвищенню науковості та доступності, значному підсиленню пізнавальної діяльності учнів, підвищенню якості їх знань та вмінь, а також створюють умови для всебічного розвитку особистості.

Разом з тим міжпредметним зв'язкам притаманний і організаційний аспект. Їх реалізація дає можливість економно у часі визначити структуру навчального плану, програм, підручників, що сприяє раціоналізації навчального процесу в цілому.

Зв'язки між знаннями з окремих предметів, що стосуються змісту навчального матеріалу зумовлені:

1) вивченням одних і тих самих фактів (явищ, процесів, подій);

2) вивченням одних і тих самих понять;

3) зумовлені застосуванням одних і тих самих законів, теорій, формуванням світоглядних ідей.

Під час реалізації на практиці міжпредметних зв'язків виникає потреба враховувати взаємне розташування в часі вивчення навчального матеріалу в курсах різних предметів.

Це зумовлює потребу класифікувати міжпредметні зв'язки за часовою (хронологічною) ознакою. Хронологічно зв'язки поділяються на:

• попередні (строк дії 2-3 роки) - під час вивчення матеріалу відповідного курсу здійснюються посилання на раніше отримані знання з інших предметів, тобто матеріал однієї дисципліни виступає основою і складовою частиною базових знань при вивченні подібної теми з іншої дисципліни. (наприклад, знайомство з римською нумерацією чисел у 6-му класі на уроках математики стає основою для засвоєння історичних подій на уроках історії, починаючи з 7-го класу; під час вивчення теми розчини на уроках хімії використовуються вміння учнів розв'язувати задачі на відсотки за допомогою пропорцій, які вивчили в 6-му класі);

• супутні (діють 1 - 2 роки) - вивчаючи новий матеріал його пов'язують з темою, яка в іншому навчальному предметі розглядається майже одночасно. Прикладом таких зв'язків є навчання учнів у пропедевтичний період, під час якого всі предмети (образотворче мистецтво, ручна праця, математика, рідна мова тощо) спрямовані на засвоєння учнями властивостей предметів та явищ, на розвиток у них просторових, кількісних та часових уявлень. Прикладом може бути одночасне вивчення такого поняття як «масштаб», тощо.

• перспективні (діють 4 - 6 років) - це зв'язки навчального матеріалу двох і більше дисциплін, які діють протягом кількох років і вивчення матеріалу значно випереджає його розгляд в інших навчальних предметах. Яскравим прикладом перспективних зв'язків є зв'язок математики та трудового навчання: вивчаючи на уроках математики геометричні фігури та їх властивості учні закріплюють відомості про них на уроках трудового навчання, удосконалюють свої знання, вчаться виділяти їх в навколишньому середовищі, практично тренуються у їхньому виготовленні [5].

Реалізація основних завдань математики неможлива без її тісного зв'язку з іншими навчальними дисциплінами. При цьому потрібно зазначити, що застосування математичних знань можливе під час вивчення інших предметів так само, як і використання матеріалу з історії, природознавства, української мови, трудового навчання, малювання тощо на уроках математики.

Для успішного здійснення міжпредметних зв'язків учитель у кожному конкретному випадку повинен орієнтуватися для вивчення якого навчального предмету може стати у нагоді той чи інший математичний факт і чітко усвідомлювати, з якою метою і в якій формі встановлюється зв'язок. Кожна прикладна задача виконує різні функції, що за певних умов виступають явно або приховано. Міжпредметні зв'язки — це не тільки «мости» між навчальними предметами, але і засіб побудови цілісної системи навчання на основі спільності змісту знань і методів наукового пізнання. Вони можуть здійснюватися у двох напрямах:

різні природничі науки виступають джерелом задач для математики;
математичні теорії стають інструментом досліджень у природничих науках.

Математиці властива універсальна застосовність, однак вона при цьому не може змінити методи й поняття тих конкретних наук, де її застосовують. У цьому сенсі вона має прикладний, підпорядкований характер. А тому доцільно узгоджувати в часі й за темпами вивчення програму з математики з програмами інших предметів шкільного компонента, що використовують математичний апарат.

Так у 5-6 класах на уроках математики вивчають дії з раціональними числами. Вміння виконувати ці дії необхідні при розв'язанні задач на уроках фізики, хімії, деяких тем з географії. Тому доцільно вже в 5-6 класах проводити підготовчу роботу, направлену на знайомство учнів з цими науками: повідомити, що такі науки взагалі існують, що саме вони вивчають, що їх об'єднує.

Ще більше можливостей реалізувати міжпредметні зв'язки з'являється в старших класах, коли учні вже вивчають фізику, хімію і на власному досвіді переконуються, що інколи на уроках з різних предметів розглядаються однакові поняття. Розглянемо декілька можливих напрямів здійснення міжпредметних зв'язків між курсом математики та іншими шкільними дисциплінами.

Приклади міжпредметних зв'язків математики й інших дисциплін

Навчальний предмет	Питання програми математики у 5 чи 6 класі	Навчальний матеріал
Інформатика	Двійкова система числення
Інформатика	Алгоритм і блок-схема	Розв'язування рівнянь та їх систем за схемами
Фізика	Переведення одиниць вимірювання швидкості, густини	Одиниці вимірювання часу і довжини, маси і об'єму
	Об'єм і маса тіл	Обчислення об'ємів геометричних тіл
	Закон додавання швидкостей	Рух за течією і проти течі
	Коефіцієнт корисної дії. Вологість повітря.	Відсотки
	Паралельне з'єднування провідників, конденсаторів. Формула тонкої лінзи	Додавання дробів із різними знаменниками
	Ізохорний процес. Ізобарний процес Залежність питомого опору металів від температури	Пряма пропорційність
	Правило важеля. Рух рідини по трубах. Ізотермічний процес.	Обернена пропорційність
	Правила Кіргофа для замкненого кола	Додавання додатних і від'ємних чисел
	Рівномірний рух, рівно змінний рух	Лінійна та квадратична функція, арифметична прогресія
	Шлях при рівноприскореному русі, вільне падіння	Квадратні рівняння, графік квадратичної функції
	Закони додавання швидкостей. Рух за течією і проти течії	Нерівності, алгебраїчні рівняння
Астрономія	Обчислення відстаней між різними космічними об'єктами	Задачі на рух
	Календарі	Додатні, від'ємні числа. Задачі на час
	Карта зоряного неба	Вимірювання кутів
Хімія	Відносна атомна маса елемента. Періодична таблиця Менделєєва	Округлення десяткових дробів
	Обчислення з використанням масової частки (%) розчиненої речовини. Обчислення масової частки (%) виходу продукту. Знаходження маси компоненту суміші Степінь електролітичної дисоціації	Відсотки, відсоткові розрахунки, алгебраїчні рівняння
	Розрахунки за рівняннями хімічних реакцій	Властивості пропорції
	Складання рівнянь окислювально- відновних реакцій.	Додавання додатних і від'ємних чисел
	Схема електронного балансу	Додавання додатних і від'ємних чисел
Біологія	Кількісні порівняння	Відсотки, графіки і діаграми
Біологія	Закони Менделя (гомозиготне та гетерозиготне схрещення)	Задачі на частини. Пряма пропорційність
Географія	Масштаб	Масштаб
	Порівняння площ країн, морів, океанів, висоти гір, глибини морів, чисельності населення тощо	Порівняння чисел. Діаграми
	Графік зміни температури	Графіки (читання і побудова)
	Рельєф, читання карт	Додатні і від'ємні числа
	Географічні координати (довгота, широта)	Система координат
	Географічні координати (довгота, широта)	Вимірювання кутів
	Приріст населення	Прогресії
Економіка	Продуктивність праці	Додавання звичайних дробів. Відсотки
Економіка	Собівартість	Нерівності,геометрична прогресія
Історія	Літочислення (до н.е. і н.е.), визначення тривалості, початку чи кінця події	Задачі на час
Історія		Додавання чисел
Музика	Ритмічне ділення	Звичайні дроби
Креслення	Масштаб	Масштаб
Креслення	Розгортки поверхонь фігур	Розгортки геометричних тіл

На уроках сільськогосподарської праці без математичних знань учні не зможуть обчислити периметр пришкільної ділянки, визначити її площу і кількість необхідного матеріалу для посадки тієї чи іншої культури, виміряти відстань від дерева до дерева під час закладки саду тощо. В свою чергу, отримані числові дані від вимірювання площі, відстані, об'єму є основою для складання і розв'язування арифметичних задач на уроках математики і тим самим закріплюють знання школярів про ці міри.

Математичні знання широко використовуються на уроках ручної праці. Школярі вирізують геометричні фігури, обводять їх за трафаретами тощо. Під час роботи з папером вчаться правильно визначати середину аркуша, розміщувати на ньому геометричні фігури і тим самим розвивають свої просторові уявлення. Одночасно на уроках математики вже в пропедевтичний період школярі мають можливість познайомитись з такими ознаками, якими постійно будуть користуватися під час трудової діяльності.

Широкі зв'язки математики та трудового навчання проявляються на уроках технічної та обслуговуючої праці, де учні застосовують на практиці свої математичні знання і вміння. Так, серед швейних, столярних виробів завжди зустрічаються такі, які в своїй основі мають форму квадрата, прямокутника, трикутника і креслення яких здійснюється шляхом використання косинця, лінійки, циркуля, транспортира. Крім того, в процесі їхнього виготовлення учнями потрібно навчитись обчислювати кількість матеріалу, необхідного для одного виробу і для цілої партії товару, що вимагає знання правил та прийомів усних і письмових обчислень, усвідомлення алгоритму їх виконання.

Розглянемо, наприклад, такі задачі :

1. З листа заліза вирішено зробити відро у формі конуса з діаметром основи 40 см і висотою 60 см. Скільки потрібно заліза? (Припуск заліза на шов – 0,6см)

2. Одне вікно має розміри 1, 3 х 1,1 м. Обчисліть скільки скла піде для скління 250 таких вікон? На обріз скла йде 8% його загальної площі.

3. Скільки дощок довжиною 4,5 м і шириною 0,125 м потрібно для настилання підлоги, довжина якої 4,5 м, а ширина – 3,5 м?

4. Витрати емалевої фарби ПФ-115 на одношарове покриття становить 180 г на 1 кв. м. Чи вистачить 4 кг емалі, щоб пофарбувати стіну завдовжки 6м і заввишки 4м?

5. Діаметр каструлі 44 см, а висота 32 см. Скільки літрів води вона вміщує?

6. Скільки меду можна вмістити в посудину, що має циліндричну форму з діаметром основи 22 см і висотою 46 см, якщо густина меду 1350кг/м³

7. Знайти об’єм циліндричної склянки, якщо довжина її кола основи 25,1 см,а висота 8 см. Скільки води вона вміщує?

Тісно переплітається математика з українською мовою. На цих уроках вчитель працює над розвитком мовлення школярів, виправленням наявних порушень звуковимови або інших його сторін, збагаченням словникового запасу новими термінами, які будуть використовуватись в процесі спілкування, формуванням чітких, лаконічних, граматично і стилістично правильних висловлювань. Запис відповіді на головне запитання задачі закріплює в учнів знання правил правопису. В свою чергу, на уроках читання і письма формується техніка швидкого, правильного, виразного читання, що сприяє кращому усвідомленню змісту арифметичної задачі, розумінню викладеної в ній ситуації.

Математика тісно пов'язана з образотворчим мистецтвом, і особливо з таким його напрямком, як декоративне малювання. На цих уроках учні вчаться малювати орнаменти з геометричних фігур, оптимально розміщувати малюнок на аркуші, співвідносити певні пропорції тощо, що дозволяє закріплювати також знання назв геометричних фігур, співвідносити з їхнім зображенням.

Широко застосовуються математичні знання на уроках природознавства, географії та історії. Під час вивчення таких тем, як "План", "Масштаб", "Земна куля" тощо учні вимірюють площу класу, шкільної ділянки, що сприяє формуванню креслярських і вимірювальних навичок. Школярі також обчислюють відстані між містами, селищами, закріплюють знання про об'ємні геометричні тіла. На уроках історії вчитель використовує знання учнів з математики під час формування уявлень про час, його відлік, обчислення тривалості тієї чи іншої історичної події. Ці дисципліни дають матеріал для складання і розв'язування арифметичних задач на уроках математики.

Крім того, для учнів буде цікавим і той факт, що, наприклад відомий імператор Франції Наполеон вільний час присвячував заняттям математикою. Йому приписують таку красиву теорему : «Якщо на сторонах трикутника в зовнішній бік побудувати рівносторонні трикутники, то їхні центри будуть вершинами рівностороннього трикутника». Цей трикутник називається зовнішнім трикутником Наполеона.

Уроки фізкультури мають також важливе значення для формування в учнів математичних понять і залежностей. Саме на них школярі знайомляться з величинами, які не можуть собі уявити абстрактно: довжину в 1 кілометр, швидкість руху людини тощо. Наприклад : 1. В змаганнях по стрільбі за кожний промах в серії з 25 пострілів стрілок отримує штрафні бали: за перших промах – 1 штрафний бал, за кожний наступний на 0,5 бала більше, ніж за попередній. Скільки разів потрапив в ціль стрілок, що отримав 7 штрафних балів? 2. Альпіністи в перший день підняття піднялися на висоту 1400 м, а потім кожний наступний день вони проходили на 100 м менше, ніж за попередній. За скільки днів вони підкорили висоту в 5000 м?

Велике значення має розкриття у доступній формі прикладного значення математики в житті та трудовій діяльності людини (під час удосконалення технологій та виготовлення продукції, здійснення покупок і розрахунків за комунальні послуги, планування та ведення сімейного бюджету тощо). Особлива увага відводиться бесідам та розв’язанням арифметичних задач, спрямованих на розвиток економічних знань:

1. Щомісячна оплата за радіо становить 4 гри. Абонент прострочив оплату на 25 днів. Яку суму він має сплатити, якщо за кожний прострочений день нараховується пеня у розмірі 1%?

2. У банк, що виплачує 16% річних, покладено 600 грн. У яку суму перетвориться цей вклад через 2 роки?

3. На якій термін банк надав позику в розмірі 4800 грн., якщо, повертаючи кредит, позичальник сплатив 9150 грн., а річна відсоткова такса дорівнює 25 %?

4.Продуктивність праці на заводі щороку збільшується на однакову кількість відсотків. За три роки вона зросла на 33,1 %. На скільки відсотків щороку збільшувалася продуктивність праці?

Всі ці задачі мають прикладний характер і для розв’язування потребують створення математичної моделі.

В той же час великі можливості в реалізації міжпредметних зв'язків мають і уроки математики. Існує декілька шляхів практичного здійснення таких зв'язків. Один з них - використання задач, які за формою та змістом відносяться до різних питань техніки, виробництва, науки тощо.

Цікавим і перспективним є такий спосіб демонстрації зв’язку математики з іншими науками, як проведення інтегрованих уроків. Інтегрований урок – це урок, який проводиться з метою розкриття загальних закономірностей, законів, ідей, теорій, відображення у різних науках та відповідних навчальних предметах. Це уроки інтегрованих зв’язків декількох предметів. Такі уроки дають можливість формування і яскравішого уявлення навколишнього, взаємозв’язків і явищ. Основний акцент припадає не стільки на засвоєння певних знань, скільки на розвиток освітнього мислення.

Структура таких уроків відрізняється чіткістю, компактністю, стислістю, логічною взаємообумовленістю навчального матеріалу на кожному етапі уроку, великою інформативністю, об’ємністю матеріалу. Інтегровані уроки передбачають обов’язковий розвиток творчої активності учнів, розподіл навантаження за рахунок переключення на різноманітні види діяльності; підвищують пізнавальний інтерес, сприяють розвитку у школярів мислення, уваги, пам’яті, мовлення, уяви.

Інтегровані уроки сприяють:

більш повному осмисленню учнями навчального матеріалу, різні аспекти якого не можуть бути розкриті засобами якогось одного навчального предмета;
формуванню умінь переносити знання з однієї галузі науки чи мистецтва в іншу;
стимулюванню аналітико-синтетичної діяльності учнів, розвитку потреби в системному підході до об’єкта пізнання, аналізу та порівнянню процесів та явищ;
розвитку творчих здібностей учнів: уяви, фантазії, образного мислення, інтелекту та емоційної сфери.

На таких уроках яскраво виражена прикладна спрямованість, тому вони викликають незаперечний пізнавальний інтерес учнів. Вони сприяють встановленню логічних зв’язків між поняттями, допомагають робити знання сучасних учнів ціліснішими, дозволяють позбутися ефекту „клаптикової ковдри”, на них формується науковий світогляд. Такі уроки сприяють встановленню логічних зв’язків між предметами, попереджають формалізм у знаннях. Наприклад, уроки математики можна інтегрувати з уроками трудового навчання в такому поєднанні: „Формули. Побудова креслень одягу”, „Одиниці маси. Робота з харчовими продуктами. Приготування страв”; з уроками географії так: „Масштаб. Побудова плану шкільної території”; з уроками природознавства: „Симетрія. Симетрія в природі”; з уроками фізики: „Швидкість. Одиниці вимірювання швидкості”; з уроками історії: „Подорож у минуле геометрії”, „Сім чудес світу” тощо. Інтегровані уроки мають яскраво виражену прикладну спрямованість і тому викликають незаперечний пізнавальний інтерес учнів [10].

1.4. Взаємозв’язок принципу історизму та прикладної спрямованості математики

На перший погляд може здаватися, що історизм у викладанні математики та її прикладна спрямованість не пов'язані. Але якщо врахувати, що більшість понять класичної математики, що потрапили до шкільного курсу, зобов'язані своїм виникненням практичним потребам людини, то цей зв'язок стає очевидним.

Про роль історії науки дуже влучно сказав Г. Лейбніц: «Дуже корисно пізнати справжнє виникнення чудових відкриттів, особливо таких, що були зроблені не випадково, а силою думки. Це приносить користь не стільки тим, що історія воздає кожному своє і спонукає інших добиватися таких самих похвал, скільки тим, що пізнання методу на видатних прикладах веде до розвитку мистецтва відкриття».

Усім відомий історичний факт відкриття у 1846 р. невідомої до того часу планети Нептун, її орбіту обчислили незалежно один від одного вчені Адамс і Левер'є. Відкриття планети «на кінчику пера» сприяло зростанню довіри до математики та створеної з її допомогою наукової картини світу.

Пошуки розв'язків окремих прикладних задач спонукали вчених розробляти нові методи досліджень, створювати досконаліші алгоритми, відкривати невідомі закономірності, що, у свою чергу, сприяло розвитку математичної науки.

Звернення до конкретних фактів з історії розвитку математики та вивчення математичних об'єктів розкриває практичний зміст математичних понять, пробуджує пізнавальний інтерес учнів до науки. Ще Г. Лейбніц підкреслив, що «Хто хоче обмежитись сучасним, без знання минулого, той ніколи сучасного не зрозуміє»

Включення елементів історії розвитку науки, техніки дозволяє вирішувати низку педагогічних задач:

підвищення інтересу до вивчення предмету;
формування загальної культури учнів;
формування наукового мислення;
гуманістичне виховання.

Під час вивчення курсу математики використовую елементи історизму. Так, наприклад, коли йде мова про те, яка геометрична фігура з-поміж фігур з одноковим периметром має найбільшу площу, не обминаю так звану задачу Дідони. «Фінікійська царівна Дідона, рятуючись від свого брата, тирана Пігмаліона, відпливла з рідного міста Тіра з невеличким загоном прибічників. Було це, якщо вірити легенді, приблизно 825 року до н. е. Довго пливли Дідона та її супутники Середземним морем, поки не пристали до берега Африки. Мешкали в тій місцевості ну мідійці. Чужинці їм були ні до чого. Проте Дідоні нікуди було подітися, місце їй сподобалося, й царівна почала благати нумідійського царя Ярба продати їй трохи землі. Бажаючи, вочевидь, здихатися надокучливої фінікіянки, Ярб заправив шалену ціну за клаптик землі, який можна обгорнути однією бичачою шкурою. На його подив і розчарування, Дідона прийняла цю знущальну пропозицію, розплатилася і подалася відміряти свою землю. Тільки вона не стала розстилати шкуру на березі. Спершу вона її розрізала так, що вийшов тонкий шкіряний ремінець (а він вийшов довгим – предовгим!), і цим ремінцем обмежила чималу ділянку, на якій і заснувала згодом велике місто Карфаген. Ярб шаленів: так, як його, мало кого пошили в дурні за всю історію людства. Та він був чесною людиною і дотримав слова – земля залишилася за Дідоною.

Так це було чи ні – тепер важко сказати. Але, між іншим, карфагенська цитадель називається Бирса, що й означає «бичача шкура».

Тож задача, яку довелося розв’язати Дідоні, є такою: яку найбільшу площу можна обмежити мотузкою заданої довжини ? Чи інакше: яка геометрична фігура з поміж фігур з однаковим периметром має найбільшу площу? Виявляється, круг.

Ця задача – одна з широкого кола ізопериметричних задач – про співвідношення площ фігур з рівними між собою периметрами, яка виникла із потреб життя. Так, з усіх трикутників з однаковою сумою довжин сторін найбільшу площу має рівносторонній трикутник; з усіх прямокутників – квадрат. А з усіх тіл з однією й тією самою площею поверхні найбільший об’єм має куля. Недарма круг і куля вважалися в давнину найдовершенішими серед усіх геометричних об’єктів.

Виявляється відповідь на задачу Дідони знали ще давні греки. Проте доказ того, що найбільшу площу з-поміж фігур рівного периметра має круг, був знайдений лише в XVIII ст. великим Леонардом Ейлером. Для цього йому довелося створити новий розділ математики – варіаційне числення.

Цікавими є також історичні факти, де на практиці застосовуються вже винайдені раніше властивості чи ознаки. Так, скажімо, ознаки подільності використовувалися при дослідженні числа так званих «щасливих» квитків. Нині в трамваях, тролейбусах та автобусах квитки продають кондуктори, а колись ця процедура відбувалася в режимі самообслуговування: пасажири власноруч кидали гроші до каси й відривали квитки. Кожен квиток мав шестизначний номер, наприклад, 286358. цей квиток у Києві вважали «щасливим», оскільки сума його перших трьох цифр – 16 – дорівнювала сумі решти трьох цифр. Тут – бо й виникла задача: наскільки часто зустрічаються «щасливі» квитки, точніше, скільки «щасливих» чисел серед чисел від 000000 до 999999 ? А от у Харкові «щасливими» вважалися квитки, в яких сума цифр, що стоять на парних місцях, дорівнює сумі цифр, що стоять на непарних місцях. Коли трохи поміркувати, то неважко збагнути, що «щасливих» квитків «по київські» стільки ж, скільки й «по харківські». Насправді «щасливих квитків 55252, тобто кожен 18-й квиток [19].

Наслідуючи принцип історизму і враховуючи фактор зацікавленості учнів, наприклад після закінчення вивчення поняття функції, границі, похідної буде доречним стисло подати історичний шлях формування цих понять (у працях Ньютона, Даламбера, Лейбніца, Ейлера та інших).

Історичні екскурси можуть дати учневі повне уявлення про закономірності розвитку науки і техніки протягом історії людства, формування цивілізацій; сприяти розвитку його науково-технічного світогляду. Учень буде ознайомлений з основами сучасної науки, зрозуміє роль науки і техніки в житті, в розвитку матеріальної і духовної культури людства.

«Історичний підхід у навчанні служить сильним і дієвим засобом у боротьбі з догматизмом і формалізмом, сприяє свідомому засвоєнню математичних знань і формуванню творчої особистості» (В. Г. Бевз).

У математиці принцип історизму тісно пов’язаний із принципом прикладної спрямованості.

Щоб підготувати учнів до життя, суспільно-корисної праці, на думку О.Я.Савченко, школа повинна особливу увагу звертати на ті питання програми, з якими можуть зустрічатися її вихованці в житті. В цьому полягають і практичні цілі навчання математики.

Прикладні задачі, особливо ті, які не втратили своєї актуальності впродовж століть, забезпечують гармонійну взаємодію учнів із суспільством.

На своїх уроках я систематично розв’язую з учнями задачі прикладного спрямування, тому що їх використання спрямоване на формування у школярів системи знань, умінь та навичок, робота з ними розвиває вміння осмислювати зміст понять та застосовувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння, висновки, розширює світогляд учнів.

Тестові арифметичні задачі відображають типові життєві ситуації, тому кожну з них можна сприймати як документ свого часу, а збірник задач як збірник документів. Наприклад: 1. За місце всередині вагона конки платять 5 коп., а за місце з двору 3 коп. З 22 пасажирів 13 сиділо всередині вагона. Скільки грошей повинні заплатити всі пасажири ? Конка – кінна залізна дорога; трамвай, який рухався за допомогою кінної тяги. Бідні пасажири їздили на відкритій площадці, а багаті - всередині.

2. Одного разу багач уклав вигідну, як йому здавалось, умову з людиною, яка цілий місяць щоденно повинна була приносити по 100 тис рублів, а натомість в перший день місяця багач повинен був віддати 1 копійку, в другий – 2 копійки, в третій – 4 копійки, в четвертий – 8 копійок, і т.д. протягом 30 днів. Скільки грошей отримав багач і скільки він віддав? Хто виграв від цієї угоди?

Таким чином, реалізуючи на уроках математики принципи історизму та прикладної спрямованості, вчитель досягає:

опанування навичок застосування учнями базових математичних понять у контексті повсякденного життя та в процесі трудової діяльності;
зростання інтересу школярів до вивчення математики і в цілому до навчання;
розвитку духовних цінностей особистості: витонченості логічних міркувань, математичного мислення, повагу до вчених минулого;
формування гуманістичної системи спілкування між учителем та учнями, перетворення кожної дитини на самостійно мислячу особистість, здатну поважати себе й інших.

І. ДОБІРКА ПРИКЛАДНИХ ЗАДАЧ

2.1 Алгебраїчні задачі

задачі на рух

1. Автомобіль, рухаючись із середньою швидкістю v км/год, пройшов s км. Який шлях за той самий час пройде мотоцикліст із середньою швидкістю u км/год ?

2. Поїзд біля телеграфного стовпа проходить за 20 с., а біля моста довжиною 80 м – за 25 с. Яка довжина поїзда ? Яка швидкість поїзда ?

3. За течією човен проплив відстань від однієї пристані до іншої за 4год., а на зворотний шлях витратив 6 год. Знайдіть власну швидкість човна і відстань між пристанями, якщо швидкість течії 2,5км/год.

4. Михайлик і Віталій вийшли назустріч один одному із двох сіл, відстань між якими 20 км. Швидкість Михайлика 6 км/год., а Віталія – 4км/год. Одночасно з Михайликом назустріч Віталію вилетіла муха. Долетівши до Віталія, вона розвернулася і полетіла до Михайлика, і так літала між ними доти, поки вони не зустрілися. Скільки кілометрів налітала муха, якщо її швидкість 11км/год.?

5. За начальником одного з відділів зранку заїжджала машина й привозила його на роботу у визначений час. Якось начальник вирішив прогулятися. Він вийшов за годину до приїзду машини й пішов їй назустріч. Дорогою він зустрів машину і прибув на роботу на 20 хвилин раніше, ніж звичайно. Скільки часу тривала прогулянка?

6. Відстань між двома містами пасажирський потяг проходить за 20 годин, а товарний – за 40год. Обидва потяги вийшли одночасно назустріч один одному. Яка частина всього шляху буде між ними через 5 годин?

7. З двох міст, віддалених одне від одного на 1680км, вийшли одночасно назустріч один одному 2 потяги. Перший потяг проходить усю відстань за 21 год., а другий – за 28 год. Через скільки годин вони зустрінуться ?

8. Із двох міст, відстань між якими 648км, виїхали назустріч один одному автомобілі «Опель» і «Таврія» і зустрілися через 4 години. Знайдіть швидкість «Таврії», якщо вона на 22км/год. менша, ніж швидкість «Опеля».

9. Швидкість польоту яструба складає швидкості польоту ворона. Знайдіть швидкість польоту кожного птаха, якщо відомо, що, розлетівшись у різні боки, за 8 хвилин обидва птахи разом подолають 12км?

10. Михайлик і Віталик їхали вниз ескалатором. Посередині ескалатора хуліган Михайлик зірвав з Віталика шапку і кинув на протилежний ескалатор. Потерпілий Віталик побіг угору ескалатором, щоб потім спуститися вниз і повернути шапку. Хитрий Михайлик побіг ескалатором униз, щоб потім піднятися вгору і встигнути швидше, ніж Віталій. Хто встигне раніше, якщо швидкості хлопців відносно ескалатора сталі і не залежать від напрямку руху?

11. Сашко йде від будинку до школи 30 хвилин, а його брат Петро – 40 хвилин. Петро вийшов із будинку на 5 хвилин раніше від Сашка. Через який час Сашко наздожене Петра?

12. Від причалу вниз по річці пустили пліт, який рухається зі швидкістю 4 км/год. Через 3 години за ним вийшов буксир. Його власна швидкість – 6 км/год. Через скільки годин буксир наздожене пліт?

13. Лисиця знаходиться попереду собаки на 60 своїх стрибків, 3 стрибки собаки дорівнюють 7 стрибкам лисиці. За один і той же час собака робить 6 стрибків, а лисиця – 9. Через скільки стрибків собака наздожене лисицю?

14. Собака женеться за мисливцем зі швидкістю 64 м/хв., а мисливець втікає від неї зі швидкістю 73 м/хв. З якою швидкістю змінюється відстань між собакою і мисливцем? Якою вона буде через 8,3хв, якщо зараз між собакою і мисливцем 58,6 м?

задачі на роботу

1. Тракторист повинен виорати ділянку поля за t годин при нормі а гектарів за годину. За який час тракторист обробить ту саму ділянку, якщо за годину він оратиме на 0,1 га більше норми?

2. Два автомобілі перевезли за день 82 т зерна. Вантажність одного автомобіля 8 т, а другого — 6 т. Скільки рейсів могли зробити автомобілі?

3. Одна друкарка може надрукувати рукопис за З год, а друга - за 5 год. За скільки годин вони надрукують рукопис разом?

4. Об'єм робіт на будівництві збільшився на 50 %, а продуктивність праці - на 20 %. Як змінилось число робітників?

5. У зв'язку з підвищенням продуктивності праці час, який потрібний для виконання певної роботи, зменшився на 28 %. На скільки відсотків підвищилась продуктивність праці?

За одну годину верстат-автомат виготовив 300 деталей. Після реконструкцій він почав виготовляти за годину 375 таких самих деталей. На скільки відсотків підвищилась продуктивність праці ?.

7. Дві бригади одночасно опрацювали ділянку землі за 12 годин. За який час могла б опрацювати цю ділянку кожна бригада окремо, якщо швидкості виконання роботи бригадами відносяться як 1:2?

8. Два ковалі, працюючи разом, можуть виконати певну роботу за 8 днів. За скільки другий коваль може виконати цю роботу сам, якщо перший коваль виконує її за 12 днів?

9. Дві снігоочисні машини можуть прибрати сніг за 6 год. Після трьох годин спільної роботи першу машину послали на інший район селища, а машина, що залишилася, закінчила прибирати за 5год. За скільки годин кожна з машин окремо може виконати всю роботу?

10. Тарас з Олегом виготовили ящик для за 25 хв., працюючи разом. Такий самий ящик Тарас виготовляє за 45 хв. самостійно. За який час зможе виготовити ящик для квітів Олег? (Відповідь округлити до десятих хвилини)

11. Перший робітник може виготовити замовлену партію деталей за 10 год., а другий таку саму партію – за 8 год. Спочатку вони виготовили 20 деталей, а потім перший робітник 2 год. працював сам, після чого вони ще 3 год. працювали разом. Скільки деталей вони зробили?

12. Один фонтан наповнює басейн за 2 год, а другий за 3год. За який час наповнять басейн обидва фонтани разом?

13.Один тракторист може зорати поле за 14 год., а другий – за 8 год. Яку частину поля вони зорють разом, якщо перший працюватиме 3 год., а другий – 2 год.?

14. Через кран у бак вливається 70 відер води щогодини, а через зливний отвір виливається 50 відер води щогодини. Скільки відер води наллється у бак, якщо і кран, і зливний отвір будуть відкриті 4год.?

15. Фрекен Бокк повинна випекти 16 тістечок за 4 години. Скільки тістечок повинна випікати щогодини Фрекен Бокк, якщо Карлсон щогодини «цупить» по 6 тістечок?

Задачі на суміші, розчини, сплави

1. Сплав містить 83% алюмінію, 10% цинку і 7% олова, причому цинку на 2,7г більше ніж олова. Чому дорівнює маса сплаву?

2. У воді розчинили 180г солі й одержали 12-відсотковий розчин солі. Скільки грамів води використали для приготування розчину?

3. (стародавній спосіб розв’язання задач на змішування речовин, правило «золотої рибки») У деякої людини були масла на продаж: одне вартістю 10 гривень за відро, друге – 6 гривень за відро. Які частини цих масел потрібно взяти, щоб дістати відро масла вартістю 7 гривень?

4. (на застосування правила «золотої рибки») Є срібло: одне одинадцятої проби, інше – чотирнадцятої. Скільки якого срібла потрібно взяти, щоб отримати 1 фунт срібла дванадцятої проби?

5. Скільки грамів 45-відсоткового розчину солі можна дістати із 300г рідини, що містить 30% солі?

6. Відомо, що 320г. одного розчину містять 112г. солі, а 440г. іншого розчину – 176г. солі. В якому розчині, першому чи другому, вищий відсотковий вміст солі?

7. Сплав міді із сріблом важить 660г. Маса срібла в 5,6 разів більша від маси міді. Скільки в сплаві окремо срібла і міді?

8. Сплав складається з олова, міді та сурми, взятих у відношенні 1:2:5. Скільки грамів сурми у сплаві, якщо міді в ньому 6,8 г? Яка маса сплаву?

9. Відомо, що 320г. одного розчину містять 112г. солі, а 440г. іншого розчину – 176г. солі. В якому розчині, першому чи другому, вищий відсотковий вміст солі?

10. Сплав масою 117кг складається з міді і цинку, маси яких відносяться як 4:5, якого металу у сплаві більше і наскільки кілограмів?

11. Деталь містить: 28% міді, 56 % заліза, 144 г – нікелю .Скільки грамів важить деталь?

12. Скільки води потрібно долити до 25 г 90-відсоткової кислоти, щоб одержати 75-відсоткову кислоту?

13. Купили 1,6 кг цукерок двох сортів по 6,8 грн. та 8,4 грн. за 1 кг і змішали їх. Ціна 1 кг суміші дорівнювала 7,5 грн. Скільки купили тих і інших цукерок.

14. Є срібло 850-ї проби і 720-ї проби. Скільки потрібно взяти срібла кожного виду щоб одержати 1 кг 40г сплаву 800-ї проби ?.

15. Скільки слід додати міді до 5 г золота 840-ї проби, щоб одержати золото 750-ї проби?

задачі на пряму і обернену пропорційність

1. З 0,3т свіжих яблук вийшло 57кг сушених. Скільки можна одержати сушених яблук з 210 кг свіжих?

2. Для будівництва стадіону п’ять машин розчистили територію за 3,5 години. За який час розчистять цю територію сім машин ?.

3. З 2,5 кг соняшників одержують 1,8 кг чистого насіння. Скільки необхідно взяти соняшника, щоб одержати 7,5 кг чистого насіння ?.

4. За два тижні пара пугачів може піймати 85 мишей-полівок, 25 водяників-пацюків і 6 білок. Скільки тварин можуть піймати 5 пугачів за один тиждень ?.

5. Великої шкоди людям завдають мухи. Дві мухи відкладають близько 150 яєць за один раз. Скільки яєць відкладуть 75 мух протягом літа, якщо за літо виводиться приблизно вісім поколінь мух ?.

6. (складне правило трьох). За освітлення приміщення протягом 24 днів дев'ятьма лампочками, що горіли по 5 годин щодня, заплачено 21 грн. 60 к. Протягом скількох днів можна освітлювати те саме приміщення за 16,8 грн. шістьма такими самими лампочками, якщо вони горітимуть щодня по 4 години?

7. На 15 стрілах амариліса (рослина з передгір’я мису Доброї Надії) утворюється в середньому до 45 квіток, а на 8 глоксиніях (рослина з Бразилії) – 72 квітки. На скільки більше утвориться квіток на 27 стрілах амариліса, ніж на 6 глоксиніях ?.

8. Щоб вивезти товар, потрібно 20 автомобіль вантажопідйомністю 2,5 т. Скільки треба було б автомобілів вантажопідйомністю 5 т, щоб вивезти цей товар?

задачі на банківську діяльність і заробітну плату

1. Вкладник поклав до банку 2000грн. під 6% річних. Скільки грошей отримає вкладник через 1 рік; 3 роки?

2. Вкладник поклав до банку «Аваль» 15000грн. під 6% річних, а до «Ощадбанку» - 15200грн. від 5% річних. У якому банку у платника буде більше грошей через рік? Через 2 роки?

3. З каси банку видано 0,2 всіх наявних грошей, потім 0,5 остачі, після чого в касі залишилося 4млн. грн.. Скільки грошей було в банку спочатку?

4. Громадянин поклав гроші в банк на рік. Банк сплатив 18% річних, що склало 540 грн. Яка сума була покладена в банк?

5. Кредит отриманий на 12000 грн під 10% річних на залишок кредиту на 12 років зі щорічною виплатою 1/12 частини кредиту. На стільки зміняться відсоткові гроші виплату кредиту, якщо взяти цю ж суму на той самий строк під 10% від суми кредиту.

6. Результативна сума депозитного вкладу в банк на 1 рік під 16% становить 2 900 грн. Яка початкова сума вкладу?

7. Дві суми складають 10000 грн. Відсоткова такса для кожної суми дорівнює 0,001, а загальна сума прибутку складає 580 грн. Знайти кожну суму окремо.

8. Деяка сума грошей знаходилась в касі ощадного банку під 2% річних (прості відсотки). Через деякий час ця сума була взята разом з нарахованими відсотками, що склало 8502 грн. Якщо б ця сума була отримана під три відсотки річних, але строком на 1 рік менше, то відсоткові гроші з неї склали б 819 грн. Яка була сума грошей, що поклали в ощадний банк, і який час вона там знаходилась.

9. Громадянин С. зі свого вкладу (3%) у касі ощадбанку витрачає на кінці кожного року по 90 грн. з кожної тисячі. Через який час він витратить весь вклад?

10. На ощадну книжку було покладено 1200 грн. Через рік з книжки зняли 240 грн. Ще через рік на книжці стало 1071 грн. Скільки відсотків в рік нараховує каса?

11. Клієнт взяв в банку кредит в розмірі 50 000 грн. на 5 років під 20% річних. Яку суму клієнт повинен повернути банку в кінці року?

12. Два приятелі поклали в банк по 10000 грн. кожен, причому перший поклав вклад з щоквартальним нарахуванням 10%, а другий – щорічним нарахуванням 45%. Через рік приятелі отримали кошти разом з нарахованими процентами. Хто отримав більший прибуток

13. У вас є 1000 гривень і ви маєте змогу робити щомісячні додаткові внесення у розмірі 100 гривень. Який прибуток ви отримаєте за 1 рік, поклавши їх на депозитний вклад «Копилка»?

14. Обчислити прибуток вкладників вкладу «Копилка» за 5 років (у відсотках), якщо сума вкладу складає 1000 грн., а сума щомісячних додаткових внесків – 50 грн.

15. Порівняти прибуток вкладників вкладів «Звичайний» і «Складний відсоток» (при розглянутих умовах), якщо сума вкладу становить 5470 грн., а строк вкладу 5 років.

16. Яка річна відсоткова ставка повинна бути при депозитному вкладі «Звичайний», щоб через 4 роки сума вкладу подвоїлась?

17. Заробітна плата робітника 4395 грн. Із них 13% прибутковий податок, 2% - відрахування в пенсійний фонд, 1% - відрахування в фонд зайнятості, 1% - профспілковий внесок. Скільки грошей одержить робітник пісня всіх відрахувань?

18. Авансом робітник одержав 2916грн, що становить 45% його заробітної плати. Яка заробітна плата робітника?

задачі на сімейний бюджет

1. У 2000 році доходи українського населення розподілялись так:

- оплата праці та доходи від підприємницької діяльності - 49%,

- надходження від продажу товарів власного господарства -5%

- пенсії, соціальні виплати -21%

- інше 25%

Побудувати кругову діаграму та провести аналіз наведених даних.

2. Родина має річний бюджет 20 000 грн. Чи має можливість ця родина отримати наступні товари тривалого користування: музичний центр вартістю 2 000 грн., кінотеатр вартістю 10 000 грн., якщо на прожиття витрачається 60 євро щомісячно, якщо курс обміну валют 1 євро - 11 гривень?

3. Родина витрачає 18 % своїх доходів на оплату житла, 50% - на продукти харчування, 20% на різні одноразові виплати, а решта на відпочинок, що становить 5640 грн. на рік. Який річний бюджет родини?

4. У середньому на одну особу за місяць потрібна певна кількість продуктів харчування, яка наведена в таблиці.

Продукти харчування	Кількість, кг	Ціна за один кг, грн
М'ясо	3,7	50
Яйця ( дес. )	19	6,5
Риба	1,3	23,5
Цукор	2,7	9,5
Олія	1,5	14,0
Картопля	1,2	4,5
Овочі	10	4,5
Фрукти	2	12
Хліб	9,1	3,5

Обчислити видатки родини з трьох осіб на продукти харчування за один рік.

5. Щомісячна оплата за радіо становить 4 гри. Абонент прострочив оплату на 25 днів. Яку суму він має сплатити, якщо за кожний прострочений день нараховується пеня у розмірі 1%?

6. З 325 кілограмів борошна одержали 429 кілограмів хліба. З’ясувати відсоток припічки.

7. Путівка в санаторій коштує 600 грн. Службовець купує путівку за 30 % її вартості. Скільки грошей він має заплатити?

8. Службовець купив у профспілці путівку в санаторій за 30 % вартості і заплатив при цьому 180 грн. Скільки коштує путівка?

9. Путівка в санаторій коштує 600 грн. Службовець заплатив за неї 180 грн. Який відсоток вартості путівки він заплатив?

10. Ціна на автомобіль спочатку підвищилась на 20 %, а потім знизилась на 20 %. Як змінилась ціна на автомобіль після цих двох переоцінок?

11. Для приготування салату потрібно три частини редьки, дві частини картоплі, одну частину яєць і 250 г майонезу. Скільки грамів картоплі потрібно для приготування салату, якщо маса всього салату – 850г?

12. Для приготування узвару потрібно дві частини сушених фруктів, одну частину меду, одну частину цукру і 1500 г води. Скільки грамів меду потрібно для узвару, якщо його маса – 3 кг 800 г?

13. Для приготування 525 г рибного асорті потрібно взяти варену рибу, варені яйця, шпроти, вершкову олію. Маса яєць складає 20% маси риби, маса шпрот – 250% маси яєць, а маса вершкової олії – 80% маси шпрот. Скільки грамів вершкової олії потрібно для приготування рибного асорті?

14. Для приготування 1 кг 130 г пахлави потрібно взяти яйця, олію сметану, борошно. Маса сметани складає маси олії, яєць – 10% маси олії, а борошна потрібно вдвічі більше, ніж олії. Скільки грамів олії потрібно для готування пахлави?

15. Купили 3 килими і 2 дорожки за 1170 грн.. Коли знизили ціни на 10% на килими і на 15% на доріжки, то за цю покупку заплатили 1047 грн. Скільки коштував килим і скільки доріжка до зниження цін і після зниження цін?

задачі на оподаткування

1. З 2004 року прибуток громадян оподатковується за ставкою 13%. Якщо прибуток не перевищує 510 грн, то з цієї суми 60 грн. не оподатковується. Якщо прибуток перевищує 510 грн, то податок нараховується з усієї суми. Який податок буде стягнутий, якщо прибуток громадянина становив:

а) 460 грн; б) 700 грн.

2. Місячний оподаткований дохід за неосновним місцем роботи громадянина в січні становив 450 грн. і далі збільшувався щомісяця на 20 грн., Доходи, отримані не за місцем основної роботи, оподатковується прибутковим податком за ставкою 20%. Обчислити загальну суму річного податку.

3. Якщо місячний оподатковуваний дохід становить від 1021 до 1700 гривень, то прибутковий податок за основним місцем роботи обчислюється за формулою 189,55 + ( х -1020 ) х 0,3, а за неосновним місцем роботи – за формулою 0,2х де х – місячний оподаткований дохід. Який повинен бути місячний оподаткований дохід, щоб податок за основним місцем роботи був менший за податок за неосновним місцем роботи?

Заробітна плата робітника 4395 грн. Із них 13% прибутковий податок, 2% - відрахування в пенсійний фонд, 1% - відрахування в фонд зайнятості, 1% - профспілковий внесок. Скільки грошей одержить робітник пісня всіх відрахувань?

задачі на цінні папери

1. Підприємство випустило 15 звичайних акцій вартістю 350 гривень кожна. Виплачені дивіденди цих акцій в 1999 році становили 600 грн., а у 2000 році – 3 000 грн. Який прогнозований курс цих акцій можливий у 2001 році?

2. У 1996 році загальний обсяг угод, укладених на ринку цінних паперів України, становив 1994,6 млн. грн. На акції припало на 204, 8 млн. грн. більше, ніж на векселя, та на 691, 4 млн. грн. більше, ніж на облігації. Для інших цінних паперів цей показник становив 624, 9 млн. грн. Знайти обсяг операцій облігаціями, акціями та векселями окремо на ринку цінних паперів у 1996 році.

3. Ви маєте суму в 1000 гривень, яку хочете розмістити з метою отримання найбільшого доходу. Банк залучає клієнтів на депозитні вклади під 8% річних. Акціонерне товариство випустило цінні папери у вигляді 8 привілейованих акцій номінальною вартістю 250 гривень з виплатою дивідендів у розмірі 10 % та 10 звичайних акцій номінальною вартістю 200 гривень. На виплату дивідендів акціонерним товариством відведено 800 гривень. Куди краще вкласти гроші:

а) у банк; б) у привілейовані акції;

в) у звичайні акції?

задачі економічного змісту

1. Планом було передбачено, що підприємство протягом декількох місяців буде виготовляти 6000 одиниць продукції. Збільшивши продуктивність праці, підприємство стало виготовляти на 70 0диниць більше, ніж було передбачено, і на місяць раніше встановленого строку перевиконало завдання на 30 одиниць. Протягом скількох місяців було передбачено виготовити 6000 одиниць продукції.

2. Книжковий магазин сплачує видавництву 90% вартості, позначеної на обкладинці книги, а реалізує книгу за зазначеною ціною. Скільки відсотків складає націнка магазину?

3. Приріст продукції на підприємстві порівняно з попереднім роком склав за перший рік а%, за другий b%. Яким повинен бути відсоток приросту продукції за третій рік, щоб середній річний приріст продукції за три роки дорівнював с%?

4. Протягом календарного року зарплата кожного місяця підвищувалась на одне й теж саме число гривен. За червень, липень, серпень зарплата складала 9900 грн., а за вересень, жовтень і листопад 10350 грн. Знайдіть суму зарплат за весь рік.

5. На виготовлення і встановлення залізобетонного кільця колодязя заплатили 26 умовних одиниць (у.о.), а за кожне наступне платили на 2 у.о. менше, ніж за попереднє. Крім того, після закінчення роботи було сплачено ще 40 у.о. Середня вартість встановленого кільця становила 22у.о. Скільки кілець було встановлено?

6. За місяць завод виготовив продукції на 453 тис. грн., що було на 25% більше, ніж заплановано. На яку суму планували на заводі виготовити продукцію?

7. У агрофірмі на поливних землях зібрали з гектара 60,8ц пшениці. Після вирощування нового сорту пшениці урожай підвищився на 25%. Скільки центнерів пшениці збирає зараз агрофірма з 23га поливного поля?

8. У фермерському господарстві «Надія» кожен рік озимою пшеницею засівають 600га полів. Середня врожайність цієї культури в 2007 р. становила 24 ц з одного гектара. Завдяки сприятливим погоднім умовам у 2008 році озимої пшениці було зібрано на 19200 ц більше, ніж у 2007 році. Обчисліть середню врожайність озимої пшениці, вирощеної у господарстві «Надія» в 2008 році (у ц/га). (Середня врожайність сільськогосподарської культури – це відношення маси зібраного врожаю цієї культури до загальної площі полів, на яких вона була вирощена).

2.2 Задачі з геометрії

задачі на знаходження площі фігур та поверхонь

1. Одне вікно має розміри 1, 3 х 1,1 м. Обчисліть скільки скла піде для скління 250 таких вікон? На обріз скла йде 8% його загальної площі.

2. Скільки дощок довжиною 4,5 м і шириною 0,125 м потрібно для настилання підлоги, довжина якої 4,5 м, а ширина – 3,5 м?

3. В кімнаті довжиною 8 м і шириною 5 м потрібно зробити паркетну підлогу з квадратних дощечок, сторона яких 200 мм. Скільки дощечок піде на підлогу.

4. Підлога майстерні має форму прямокутника. Одна сторона прямокутника на 5 м більше другої, а площа дорівнює 84 м2. Визначити довжини сторін, для того, щоб дізнатися скільки необхідно дерева, щоб прибити плінтус.

5. Визначте потрібний за нормою час і розцінку для облицювання газованою плиткою 150х150 мм відкосів віконного пройому, розмірами 4х2, якщо ширина відкосу 30 см.

6. Витрати емалевої фарби ПФ-115 на одношарове покриття становить 180 г на 1 кв.м. Чи вистачить 4 кг емалі, щоб пофарбувати стіну завдовжки 6м і заввишки 4м?

Скільки листів шиферу потрібно для покриття даху ангару з технікою, якщо поперечний переріз даху - рівнобедрений трикутник з основою 8м і висотою 3м, а довжина даху (по коньку) 30 м ?

7. Скільки фарби потрібно на покриття покрівлі чотирисхилого (чотирискатного) даху будинку, довжина якого 12м, ширина – 8м, кут нахилу всіх схилів (скатів) 30 градусів, якщо витрати фарб складають 0,5 кг на 1 м квадратний ?

8. Підрахувати розхід матеріалу для покриття чотирьохскатного даху, якщо в його основі прямокутник зі сторонами18м і 12 м, якщо використовується кровельне залізо, кут нахилу 45°.

9. Підрахувати розхід матеріалу для покриття чотирьохскатного даху, якщо в його основі прямокутник зі сторонами18м і 12 м, якщо використовується кровельна сталь, кут нахилу 20°.

10. Розрахувати розхід масляного колектора, що йде на окраску панелі приміщення, розміри якого 4000х5000х3000, якщо на окраску 1 м² потрібно 0,2 кг(вікна і двері займають 12% площі поверхні).

11. Купол будівлі цирку лежить на правильній 12-граній призмі. Стіни цирку подвійні, скляні. Кожна секція зовнішньої стіни має висоту 9м і ширину 7,5 м. Внутрішні і зовнішні стіни розташовані симетрично відносно осі будівлі. Відстань між внутрішньою секцією і паралельною до неї зовнішньої секцією дорівнює 40 м. Визначте, скільки квадратних метрів скла пішло на покриття стін цирку?

12. Конусоподібний намет висотою 3,5м і діаметром основи 4м покрито тканиною. Скільки тканини пішло на намет?

13. Напівциліндричне склепіння підвалу має 6 м довжини та 5,8 м у діаметрі. Знайдіть площу повної поверхні підвалу.

14. Навіс над стогом сіна має форму піраміди, висота якого дорівнює 0,9м, а основа являє собою квадрат із стороною 2,5м. Визначити площу покрівлі.

Задачі на об’єми фігур

1. Скільки меду можна вмістити в посудину, що має циліндричну форму з діаметром основи 22 см і висотою 46 см, якщо густина меду 1350кг/м³

2. Діаметр каструлі 44 см, а висота 32 см. Скільки літрів води вона вміщує?

3. Скільки повних порцій супу міститься в каструлі, яка має форму циліндра, висота якого 40 см, а діаметр 0,3 м. Відомо, що одна порція містить 0,25 л супу.

4. Знайти об’єм циліндричної склянки, якщо довжина її кола основи 25,1 см,а висота 8 см. Скільки води вона вміщує?

5. Цинкове відро має форму зрізаного конусу з діаметрами основ 31 см і 22 см та твірною 27 см. Скільки матеріалів пішло на його виготовлення, якщо на шви та відходи йде 12%?

6. Завантажувальна лійка картоплечистки МОК-16 має форму зрізаного конусу. Обчислити площу її бічної поверхні, якщо радіус більшої основи дорівнює 16 см, радіус меншої основи – 9см, довжина твірної – 10 см.

7. Діаметр зовнішнього корпусу харчо варильного котла дорівнює 1 м, а внутрішнього циліндру – 80 см. Висота котла 1м 20 см. Знайти об’єм пароводяної сорочки цього котла.

8. Картоплю насипали в купу конічної форми. Довжина кола основи купи 12м, твірна -3м.Скільки тонн картоплі знаходиться в купі? Маса 1м³ картоплі 800 кг.

9. Яка врожайність зернових з 1га при розмірах поля 2 3 км та врожайності 200гр. з 1 дм². Порівняйте отриманий результат із загально обласним показником врожайності пшениці за 2010 рік (40 ц з 1 га) і зробіть висновок про ефективність сільськогосподарських робіт на даному полі.

10. Скільки мішків аміачної селітри можна помістити в склад розмірами 20м х 9м х 4м, якщо мішок селітри можна прийняти (з певною похибкою) за прямокутний паралелепіпед розмірами 90смх 5смх25см? (На щілини між мішками і центральний прохід виділяється 30% об’єму складу).

11. Скільки бетонних плит, призначених для будівництва майстерень, можна навантажити на причеп трактора МТЗ – 82, якщо максимально допустиме навантаження складає 4,5 т, розміри плит 90см на 55см на 35см, а густина бетону 2,2 т/м куб.

12. На вантаженні пшениці зі складу на автомашини працює зернонавантажувач, який подає 5т зерна за 1 год. За скільки годин безперервної роботи буде повантажена вся пшениця, якщо висота складу АА1 = 4м, ширина АВ = 8м, АД = 20м, А1Д1 = 16м, а маса 1 м куб. пшениці складає приблизно 750 кг ?

13. Будівельна бригада профтехучилища в кількості 5 чоловік за 4 години викопала вручну 30 ям, в які встановлюються опорні стовпи навісу для зберігання мінеральних добрив. Кожна яма (з певною похибкою) має форму правильної зрізаної чотирикутної піраміди глибиною 1,2 м зі сторонами основ 0,5 м і 0,4 м. на скільки відсотків виконано завдання, якщо норма часу на 1 м куб. ґрунту складає 3 години.

14. По скільки рейсів повинні здійснити два самоскиди МАЗ – 5449 вантажопідйомністю 8 т кожний для перевезення на тваринницьку ферму сінажу з траншеї, яка має форму прямокутного паралелепіпеда розмірами 15м на 4м на 3м, якщо маса 1 м куб. сінажу складає 0,6 т?

15 Паливний бак автомобіля УАЗ – 451 ДМ з певною похибкою можна прийняти за прямокутний паралелепіпед розмірами 89см на 35см на 18см, (розміри внутрішні). На скільки кілометрів вистачить повної заправки бака, якщо витрати бензину складають 12л на 100км ?

16. Бак, що має форму прямокутного паралелепіпеда, доверху заповнено бензином. Довжина бака 3м, ширина 1,5м, висота 1,2м (Розміри внутрішні). Густина бензину 710 кг/м куб. На скільки робочих днів вистачить цього бензину для заправки автомобіля ГАЗ – 53, якщо середні витрати бензину автомобіля за робочий день – 95 кг?

17. Потрібно підсипати гравій на ділянці сільської дороги довжиною 1 км та шириною 4 м, щоб рівень дороги піднявся на 25 см. По скільки рейсів з гравієм повинен здійснити кожен з п’яти самоскидів КаМАЗ – 5511, якщо кузов самоскида вміщує 7,5 м3 гравію ?

18. Будівельна бригада споруджує з цегли перегородку на складі для зберігання мінеральних добрив. Довжина перегородки 18м, висота 4м, товщина 25см. Розчин збільшує об’єм перегородки на 15%. Скільки цегли потрібно для роботи, якщо розміри цеглини 25см на 12см на 6,5см (при умові, що цегла не б'ється)?

19. Сінажна траншея являє собою в поперечному перерізі рівнобедрену трапецію з основами 5м і 8м та висотою 3м. Довжина траншеї 15м, сінаж закладено на одному рівні з краями траншеї. На скільки днів вистачить цього сінажу для тваринницької ферми, яка нараховує 80 корів, якщо щодобові витрати сінажу на одну корову складають 35кг, а маса 1м куб. сінажу становить 600кг ?

20 Для підсипки під’їзних шляхів до будівельного майданчика завезено гравій, складений в купу (з певною похибкою) правильної чотирикутної піраміди, сторони основ якої 12м, 4м, а висота 3м. Скільки кубічних метрів гравію привезено на будівельний майданчик

21. Розчин висипали у вигляді конічної кучі, твірна якої 6,3м, довжина кола С = 17,6м, чи вистачить його для кладки 190м куб. стінки, якщо для кладки 1м куб. стінки потрібно 0,23м куб. розчину ?

22. Суміш гравію з піском у вигляді конічної кучі , твірна якої 2,1м довжина кола основи конуса С = 6,28м. Якою повинна бути вантажопідйомність вантажної машини, щоб перевезти цю суміш, якщо 1 м куб. суміші має 1600 – 1900 кг ?

Задачі на розв’язування трикутників

1. Знайдіть відстань від точки А до недоступної точки В, якщо АС = 50 м, кут САВ= 80° і кут АСВ= 72°.

2. Як обчислити ширину смуги, якщо відомо відстані від деякої точки до її країв?

2. Футбольний м’яч знаходиться в точці А футбольного поля на відстані 4,5 м і 9,4 м від основ В і С стійок воріт. Футболіст направляє м’яч у ворота. Знайдіть кут α влучання м’яча у ворота, якщо ширина воріт 7м.

3. На будівництві залізниці потрібно на ділянці АВ прокласти тунель. За даними на малюнку поясніть, як знайти довжину і напрям тунелю. Обчисліть довжину тунелю.

4. Крутість яких сходів більша: в 20 східців, які піднімаються на 3 м., чи в 15 східців, які піднімаються на 2 м.

5. Пожарна драбина, яка закріплена на машині, висувається на 20 м., а її крутість може досягати 70⁰. Основа драбини знаходиться на висоті 2 м. На який поверх можна по ній піднятися, якщо висота поверху 3 м.?

6. Дороги, які сполучають села А, В і С (мал. 1), утворюють трикутник, причому дорога із села А до села С заасфальтована, а дороги із села А до села В та із села В до села С – ґрунтові. Дороги із села А до сіл В та С утворюють кут у 15⁰, а дороги із села В до сіл А і С – кут у 5⁰. Швидкість руху автомобіля по асфальтованій дорозі у 2 рази більша за швидкість його руху по ґрунтовій. Який шлях обрати водію, щоб як найшвидше дістатися із села А до села В?

мал. 1

Спортивний літак рухається по замкненому трикутному маршруту. Два кути цього трикутного маршруту рівні і 100⁰. Найменший шлях маршруту літак долає за 1 годину. За скільки часу він пролетить весь маршрут, рухаючись зі сталою швидкістю? Відповідь подайте у годинах з точністю до десятих.
Дороги із сіл А і В сходяться біля розвилки С (мал. 2). Дорога із села А до розвилки утворює з дорогою в село В кут у 30⁰, а дорога із села В з дорогою в село А – кут у 70⁰.

Одночасно із села А до розвилки виїхав автомобіль зі швидкістю 90 км/год., а із села В – автобус зі швидкістю 60 км/год. Хто з них першим доїде до розвилки?

мал. 2

9. В 12.00 год. порушник звернув з основної магістралі і помчався по шосе зі швидкістю 140 км/год. В 12.00 год. інспектор ДАІ помчався по ґрунтовій дорозі зі швидкістю 70 км/год. на переріз порушнику. Чи встигне інспектор зупинити порушника на перехресті (мал. 3)?

ДАІ

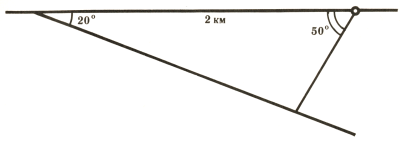
мал. 3

задачі на об’єми многогранників

1. Скільки будівельної цегли і розчину потрібно для побудови стіни довжиною 12 м, товщиною 0,5м, висотою 2,5 м, якщо 1м³ цегляної площадки містить 400 шт цеглин, а потреба в розчині складає 0,2 об’єму кладки?

2. Для доставки цегли використовують піддони. Якою повинна бути висота одного пакету цегли, якщо розміри піддона 520х1030 мм, а норма укладки в цей піддон дорівнює 800 кг?

3. Потрібно побудувати овочеве сховище з прямокутною основою. Периметр основи дорівнює 110 м, висота сховища – 15 м. Якими повинні бути розміри сховища, щоб воно мало найбільший об’єм?

4. Який об’єм молока може вміститися в тетрапак у вигляді піраміди, основа якої рівносторонній трикутник зі стороною 20 см, висотою 24 см.

5. Єгипетські піраміди – найдавніше і разом з цим єдине, що збереглося до наших днів, чудо світу. Піраміда Хеопса – сама велика піраміда. Вона була самою великою спорудою світу, поки в 1889 році не поступилась Ейфелевій башті . Зараз висота піраміди складає 137 м, основа 230х230м, вага 6400000 тонн. Вичислити об’єм піраміди.

6. Скільки літрів води вміщує водойма, що має форму правильної чотирикутної зрізаної піраміди, якщо глибина її дорівнює 1,2м, а сторони основи 10м і 5м?

7. Бак, має форму правильної чотирикутної зрізаної форми, він вміщує 190л бензину. Знайдіть глибину цього баку, якщо сторони його основ дорівнюють 60 см і 40 см.

задачі на тіла обертання

1. Висота весільного торта 8 дм, радіус основи 5 дм. Торт розрізали так, що у перерізі утворився квадрат. Знайдіть відстань від цього перерізу до осі.

2. Чан, що має форму півсфери з внутрішнім радіусом R, наповнений томатним соусом. Визначити, який об’єм рідини виллється з чану, коли нахилити його на кут альфа .

3. Водій отримав завдання перевезти землі для клумби, що має форму сегменту кулі з ріусом 5м, і висотою 60 см. Скільки кубометрів землі потрібно для облаштування клумби?

4. На будівельному майданчику знаходиться ємкість для води у формі сегменту кулі з радіусом 2м і висотою 1 м. Скільки кубометрів води вміщується в цю ємкість?

5. Студент купив в магазині гарну чашку у формі сегменту кулі і хоче дізнатися, який її вміст. Він виміряв діаметр чашки і висоту, які дорівнюють відповідно 15 см і 7 см. Знайти об’єм чашки.

6. Купол Київського цирку уявляє собою сферичний сегмент висотою 42м і діаметром основи64 м. Скільки листів перфорированого декаротивного дюралю витрачено на його покриття, якщо розмір одного листа 1,25х1,75 м?

7. Для прикрашання будівлі магазину на його даху був встановлений козирок у формі конусу. Необхідно визначити, скільки потрібно заліза на його покриття, якщо козирок має діаметр основи 2м і висоту 90 см, а листи заліза мають розміри 2х1,5 м?

8. Для прикрашання будови магазину на його даху був встановлений козирок у формі конусу. Необхідно визначити, скільки потрібно, скільки потрібно фарби, якщо козирок має діаметр основи 2м і висоту 90 см, а на 1 м витрачається 200 г фарби.

9. Діаметр Місяця приблизно складає четверту частину діаметру Землі. Порівняйте об’єми Місяця і Землі.

ІІI. ВИСНОВКИ

Не раз доводилось чути фразу про те, що математика – країна без меж. Не дивлячись на свою банальність, фраза про математику має під собою дуже вагомі підстави. Математика в житті людини займає особливе місце. Ми настільки з’єдналися з нею, що навіть не помічаємо її. Проте з математики починається все.

В школі математичних задач дуже багато і складність їх з кожним роком зростає. Вони не просто навчають дітей математиці, простим обчислювальним діям. Математичні задачі розвивають мислення, логіку, комплекс вмінь: вміння групувати предмети, розкривати закономірності, визначати зв’язки між явищами, приймати рішення. Дуже часто рішення таких задач є просто математичним розрахунком.

Заняття математикою, розв’язування математичних задач розвиває особистість, робить її цілеспрямованою, активнішою, самостійною, а прикладна спрямованість навчання математики формує в учнів розуміння математики, як методу пізнання та перетворення оточуючого світу, який має розглядатися не тільки областю застосувань математики, а й невичерпним джерелом нових математичних ідей.

Навчання математичного моделювання, застосування математичних знань до розв’язування задач прикладного змісту, що виникають поза межами математики і розв’язуються математичними методами, сприяє зміцненню мотивації навчання, системності, дієвості, гнучкості знань, активізує пізнавальні інтереси учнів. Моделювання як елемент математичної грамотності виступає засобом реалізації прикладної спрямованості навчання математики, посилює та збагачує фундаментальну математичну освіту в межах, що відведені основною школою.

Неабияке значення математичного моделювання найбільш яскраво проявляється при організації міжпредметних зв'язків, які стимулюють потяг до знань, укріплюють інтерес до предмету, розширюють зацікавленість, заглиблюють знання, сприяють становленню інтересів професійного плану. Використання міжпредметної інтеграції робить процес навчання різноманітним, цікавим, емоційно забарвленим, творчо насиченим. Забезпечується висока активність школярів у використанні знань з одного предмету на уроках з іншого і навпаки, цікаво і просто поєднуючи теоретичні знання з їх практичним застосуванням.

Перспективним є і такий спосіб демонстрації зв’язку математики з іншими науками, як проведення інтегрованих уроків. Такі уроки дають можливість формування і яскравішого уявлення навколишнього, взаємозв’язків і явищ. Основний акцент припадає не стільки на засвоєння певних знань, скільки на розвиток освітнього мислення.

Структура інтегрованих уроків відрізняється чіткістю, компактністю, стислістю, логічною взаємообумовленістю навчального матеріалу на кожному етапі уроку, великою інформативністю, об’ємністю матеріалу. Вони передбачають обов’язковий розвиток творчої активності учнів, розподіл навантаження за рахунок переключення на різноманітні види діяльності; підвищують пізнавальний інтерес, сприяють розвитку у школярів мислення, уваги, пам’яті, мовлення, уяви.

В процесі своєї роботи відмітила зростання пізнавального інтересу учнів до предметів під впливом міжпредметних зв'язків. Отже, якщо сучасний вчитель математики у процесі навчання шкільного курсу акцентує увагу учнів на зв’язок математики з життям, то він викликає у дітей інтерес до навчання, добитися формування таких важливих рис характеру як послідовність у роботі, наполегливість, акуратність, увагу, критичне ставлення до своєї роботи й роботи своїх товаришів, кмітливість, чесність, колективізм, любов до праці, культури письма й усної мови.

На мою думку, використання прикладних задач має на уроках математики важливе значення перш за все для виховання стійкого інтересу до математики. Завдяки різним задачам прикладного характеру учні будуть переконуватися в значенні математики для різних сфер діяльності людини, в її корисності і необхідності для практичної роботи і побуту; побачать різноманіття використання математичних ідей і методів поза самою математикою; зрозуміють, що повноцінна освіта сучасної людини неможлива без належної математичної підготовки, оскільки математика є опорним предметом при вивченні суміжних дисциплін. Все це безумовно сприятиме й підвищенню рівня їх математичної освіти

Швидко змінюється світ і саме життя. В неї входять нові технології. Тільки математика і розв’язування задач в традиційному розумінні не змінює себе. Математичні закони перевірені і систематизовані.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Алешина Т. Урок математики: применение дидактических метриалов с профессиональной направленостью / Т. Н. Алешина. – М.: Высш. шк., 1991. – 64 с.

2. Антоненко М. Розв’язування геометричних задач: Книжка для вчителя / М. І. Антоненко. – К.: Рад. шк., 1991. – 128 с.

3. Богуславський І. Збірник практичних задач і вправ з геометрії / І. Богуславський. – К.: Рад. шк., 1961. – 88 с.

4. Бевз Г.П. Математика: 6 кл.: Підруч. Для загальноосвіт. навч. закл. / Г. П. Бевз. –К.: Генеза, 2006. – 304 с.

5. Бевз В. Міжпредметні зв’язки як необхідний елемент предметної системи навчання / В.Бевз // Математика в школі. – 2003. – №6. – с. 6-11.

6. Бевз Г. П. Геометрія: підруч. для 10-11 кл. загальноосвіт. навч. закл / Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова . – К.: Вежа, 2002. – 225 с.

7. Возняк Г. Взаємозв’язок теорії з практикою а процесі вивчення математики / Г. М. Возняк, М. П. Маланюк. – К.: Рад. шк., 1989.-128 с.

8. Возняк Г. Прикладні задачі: від теорії до практики / Г. Возняк, О. Возняк– Тернопіль: Мандрівець, 2003 – 96 с.

9. Возняк Г. Прикладна спрямованість шкільного курсу математики / Г.М. Возняк, К. П. Маланюк. – К.: Рад. шк.., 1984. – 80 с.

10. Волосюк О. Застосування шкільного курсу математики в повсякденному житті / О. В. Волосюк, С. В. Онопченко // Вісник ЛНУ імені Тараса Шевченка – 2010. – № 17 (204).

11. Державний стандарт базової і повної середньої освіти // Математика в школі. – 2004. – № 2.

12. Козловська О. Прикладна спрямованість шкільного курсу математики. Розвиток життєвої компетентності школярів / О. Козловська // Математика. – №3. – 2008.

13. Колмакова Н.Р. Прикладные задачи как средство пропедевтики основных понятий математического анализа в школе: Дис. ... канд. пед. наук. – Красноярск, 1991. - 169 с.

14. Колмогоров А.Н. Математика в ее историческом развитии / Под ред. В. А. Успенского. – М.: Наука. Гл. ред. физ-мат. лит., 1991. – 224 с.

15. Лук’янова С. Роль прикладної спрямованості в навчанні математики учнів 5-6 класів. / С. М. Лук’янова // Вісник ЛНУ імені Тараса Шевченка. – 2010. – № 12 (199).

16. Прус А. Прикладна спрямованість стереометрії: 10-11 кл. / А. Прус, В. Швець. - К.: Шк. світ, 2007. – 128 с.

17. Програма з математики для 5-11 класів загальноосвітньої школи / Міністерство освіти і науки України. - К. - 2005.

18. Математика. Програма для загальноосвітніх навчальних закладів. — К.: Перун, 2005. — 64 с.

19. Савін П. Я пізнаю світ./ А. П.Савін, В.В. Станцо, Г. Ю. Котова – К.: Школа, 2002. – 432 с.

20. Слєпкань З. Методика навчання математики / З. І. Слєпкань. – К.: Зодіак ЕКО, 2000. – 190с.

21. Старова О.О. Реалізація міжпредметних зв’язків на уроках математики // Математика. - 2004. - № 3. - с.16-17.

22. Стерневська Т. Математичне моделювання // Математика – 2006, №11 – с. 7-11.

23. Терешин Н. А. Прикладная напрвленость школьного курса математики / Н. А. Терешин. - М.: Просвещение, 1990. - 96 с.

24. Хуторской А. Ключевые компетенции как компонент личностно – ориентированного образования / А. М. Хуторской // Народное образование.- 2003. - № 2

25. Шапиро И. Использование задач с практическим содержанием в преподавании математики: Кн. для учителя / И. М. Шапиро. – Просвещение, 1990. – 96с.

doc

Завантажити

Зберегти на потім

Додав(-ла)

Терещук Світлана Іванівна

Пов’язані теми

Математика, Методичні рекомендації

Додано

6 жовтня 2020

Переглядів

9643

Оцінка розробки

Відгуки відсутні