Методичні рекомендації до уроку геометрії на тему "Зображення фігур у стереометрії"

Побудова зображень у стереометрії

     Уявити наш сьогоднішній світ без технологій просто неможливо. Стрімка еволюція технологій призвела до дефіциту фахівців з технічних напрямків. Попит на них росте набагато швидше, ніж на інші спеціальності. У відповідь на виклики часу на перший план виходить тип освіти, що поєднує креативність та технічні знання. Це – STEM- освіта. Вона стимулює допитливість та науково-технічну творчість учнів, що дасть змогу збільшити кількість тих, хто обиратиме науково-технічні та інженерні професії. А це, в свою чергу, сприятиме підвищенню рівня конкурентоспроможності національної економіки. Елементи STEM- освіти можна використовувати на уроках математики. Надійним засобом формування в учнів просторових уявлень і здібностей до конструювання є розв'язування стереометричних задач на побудову. Такі задачі викликають в учнів жвавий інтерес, сприяють формуванню поняття естетики побудови і оформлення зображень просторових об'єктів на площині.

   Розв’язування найпростішої геометричної задачі починається з виконання правильного малюнка, бо без нього важко, а деколи і неможливо зрозуміти умову задачі, проаналізувати її і розв’язати.

   На відміну від планіметрії, де ми легко зображаємо фігуру та її елементи, стереометричні задачі мають свою специфіку. Це пов’язано з тим, що ми користуємося не просторовою моделлю, а зображенням на площині. Це приводить до певних спотворень. У зв’язку з цим потрібно вміти правильно зображати фігуру з урахуванням її властивостей і властивостей паралельного проєктування. По-друге, потрібно вміти уявити просторову модель фігури за її умовним зображенням. Бо на такому зображенні прямокутний в оригіналі трикутник не часто буває прямокутним, а мимобіжні прямі перетинаються чи паралельні. Якщо в планіметрії говориться про побудову, наприклад, перпендикуляра, то ми беремо в руки циркуль і лінійку або кутник і будуємо цей перпендикуляр. Ніяких обґрунтувань тут не потрібно. Вони випливають із способу побудови. У просторі такі побудови носять інший характер. Нехай потрібно визначити відстань від основи висоти піраміди до її бічної грані. Для цього необхідно опустити перпендикуляр з основи висоти піраміди на її бічну грань. Але в стереометрії це робиться не креслярськими інструментами, а теоретичним обґрунтуванням такої побудови, яке містить ще й пояснення того, де на бічній грані буде міститися основа даного перпендикуляра.

   Учнів слід націлювати критично ставитися до малюнка. Тому  що він, зазвичай, не повністю відповідає  умові задачі. Так, наприклад, довільний трикутник на зображенні може виглядати як рівнобедрений чи прямокутний. І це спрямовує наші думки на хибний шлях. Отже, не можна використовувати в міркуваннях властивості фігури, які видно на малюнку, якщо ми не можемо обґрунтувати їх, спираючись на твердження, доведені раніше.

   Той, хто хоче навчитися розв’язувати стереометричні задачі, повинен, перш за все, навчитися правильно зображати просторові фігури на площині. Щоб образ фігури був зрозумілішим, з усіх можливих її проєкцій вибирають таку, на якій зображено всі її частини. При цьому невидимі лінії зображають штриховими лініями, а видимі - суцільними. Перший  рисунок тієї чи іншої фігури може бути й невдалим, тому спочатку ескіз виконуємо тонкими лініями. Тільки впевнившись, що рисунок відповідає умові задачі, обводимо його видимі і невидимі лінії. Букви на малюнку надписуємо охайно по один бік від прямих та відрізків, щоб вони не перетинали інші лінії і не заважали наступним побудовам. Малюнок у планіметрії за розмірами повинен займати приблизно четвертину висоти аркуша учнівського зошита. А в стереометрії  - третину.  Центр фігури визначає перетин двох штрихів. Штрихова лінія на контурах зображень повинна починатись і закінчуватись тільки штрихами. Штрихи у лінії та проміжки між ними повинні бути приблизно однакові по всій лінії.   

  Для одержання зображень найчастіше користуються методами центрального і паралельного проєктування. Наше око бачить усі предмети в центральній проєкції. Вона дає прекрасне загальне уявлення про зображені предмети. Але її властивості та закони побудови досить складні, і тому перспектива непридатна для нашої мети.

   Безсумнівно, кожен в ясний сонячний день бачив на тротуарах, на стінах тіні предметів. Можливо, саме механізм утворення сонячних тіней підказав математикам ідею паралельного проєктування. Якщо розглядати на гладкій поверхні тіні каркасних геометричних фігур, то змінюючи положення фігури або напрям поширення променів від джерела світла, можна одержати різні зображення:  від наочних до таких, на яких фігуру неможливо впізнати. Наприклад, трикутник може відобразитися у вигляді відрізка, а тетраедр - у вигляді трикутника. Отже, малюнок просторової фігури повинен задовольняти такі основні вимоги:

• малюнок повинен бути правильним, тобто бути однією з можливих проєкцій зображуваної фігури. Лінійні розміри не беруться до уваги. Зображення має бути подібним проєкції оригіналу.
• малюнок повинен бути наочним, тобто створювати уявлення про оригінал, сприяти розвитку просторового мислення, допомагати знаходити правильний шлях до розв’язання задачі чи доведення теореми.
• малюнок повинен бути вільно виконуваним.

   Щоб вільно користуватися паралельним проєктуванням, потрібно, перш за все, з’ясувати, які властивості фігур, що проєктуються, залишаються незмінними.

1. Проєкцією точки є точка.
2. Проєкцією прямої в загальному випадку є пряма.
3. Якщо пряма паралельна  напряму проєктування, то її проєкцією є точка.
4. При паралельному проєктуванні зберігаються відношення відрізків однієї прямої чи паралельних прямих.

   Виходячи з цього, проєкція середини відрізка-оригіналу є серединою його проєкції на площину. Властивість діагоналей паралелограма - ділитися в точці перетину навпіл,  властивість основи медіани трикутника -  ділити відповідну сторону навпіл, зберігаються і на їх проєкціях. Розглянуті властивості паралельних проєкцій дають змогу одержувати  зображення просторових фігур за допомогою побудов, які виконуються повністю в одній площині.

Звідси випливає, що:

• будь-який трикутник, зображений на малюнку, можна прийняти з точністю до подібності за проєкцію трикутника будь-якої наперед заданої форми. Така невизначеність трикутника пояснюється тим, що непаралельні сторони змінюються неоднаково, а, отже, і кути трикутника при паралельному проєктуванні змінюються теж неоднаково. Тому за зображенням не можна визначити вид трикутника;

- зображенням будь-якого паралелограма, а також квадрата, ромба і прямокутника є довільний паралелограм;

     - зображенням трапеції є довільна трапеція з тим самим відношенням основ, що й в

        оригіналі.

   Зображення многогранників на площині теж мають елемент невизначеності. Щоб усунути цей недолік, слід скористатися умовою задачі або додатковими вказівками, які уточнюють вид многогранника. Зображення стереометричних фігур буде наочним, якщо:

•  многогранник розміщено перед площиною проєкції у найбільш звичному для ока положенні;
•  на зображенні подано найбільш можливе число його граней;
•  зображення окремих ребер,  діагоналей та інших елементів многогранника не зливаються;
•  при зображенні многогранників, циліндра і конуса будемо розташовувати ці тіла так, щоб їх висоти займали вертикальне положення  і зображалися вертикальними відрізками.

    Приступаючи до зображення многогранника, слід, перш за все, проаналізувати його форму і властивості. У кожному конкретному випадку треба спочатку прикинути, чи буде відповідна побудова наочною. Наприклад, висота піраміди може співпадати з одним із бічних ребер чи лежати в одній із бічних граней. У цих випадках зображати висоту довільно не можна.

  Зображення фігури є важливим, але не основним, а допоміжним етапом розв’язування задачі. А тому для економії часу необхідно прагнути виробити в учнів навички виконання малюнків від руки без креслярських інструментів.

Зображення правильної трикутної піраміди

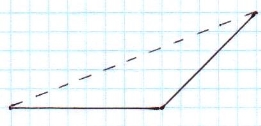
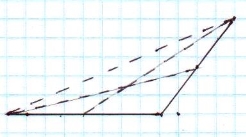
   Зображаємо довільний трикутник ABC, який будемо вважати проєкцією правильного трикутника.

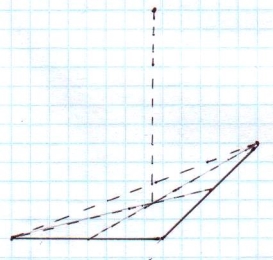
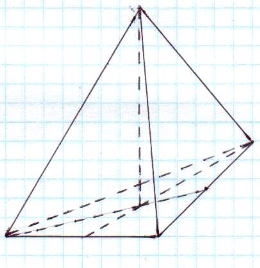
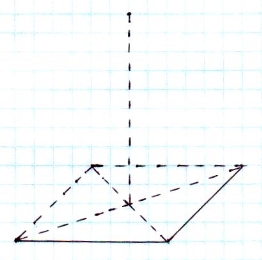
Через точку О перетину медіан трикутника ABC , яка зображає центр правильного трикутника, проводимо вертикальний відрізок OS довільної довжини, що зображає висоту піраміди. Точку S з’єднуємо відрізками з вершинами трикутника ABC .

Аналогічно будуємо зображення інших правильних пірамід.

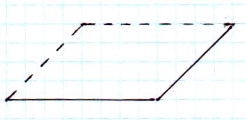
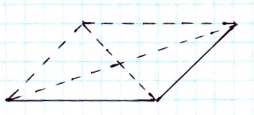
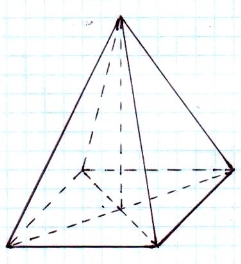
    В основі правильної чотирикутної піраміди лежить квадрат. А вище було сказано, що його зображенням є довільний паралелограм.

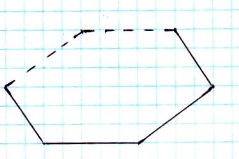
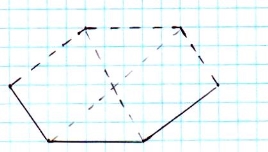
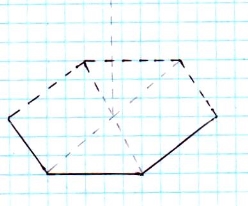
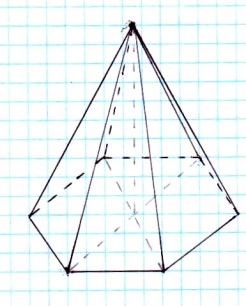
Зображення шестикутної піраміди

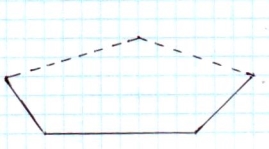
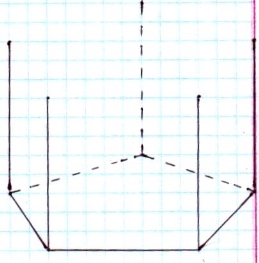
Зображення п’ятикутної призми

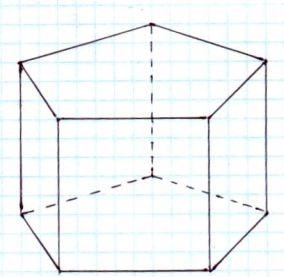
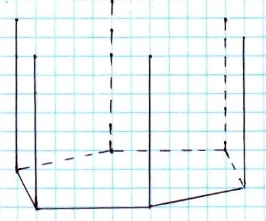
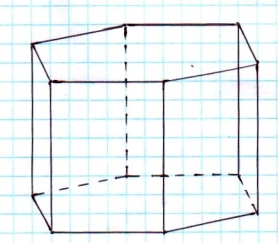
Зображення шестикутної призми

  Для побудови зображень циліндра, конуса, сфери використовують шаблони овалів різного розміру.

  Овал - це крива, утворена дугами різних радіусів, що плавно переходять одна в одну. Ці точки називаються точками спряження.

  Щоб виготовити овал для роботи вчителеві – на класній дошці, а учням – в зошиті, можна скористатися таким способом.

Нехай задано велику і малу осі овала. У системі двох взаємно перпендикулярних прямих а і b будуємо прямокутник ABCD, сторони якого дорівнюють половинам осей овала. Проводимо діагональ ВD прямокутника ABCD. З вершини C проводимо промінь перпендикулярно до діагоналі ВD до перетину з прямою b. Точки перетину променя з прямими а і b позначимо відповідно Х₁ та Y₁. Будуємо точки Х₂ та Y₂ симетричні точкам Х₁ та Y₁ відносно центра симетрії A. З точок Y₁ та Y₂, як з центрів, описуємо великі дуги овала радіусом  R₁=BY₁. З точок Х₁ та Х₂, як з центрів, радіусом R₂=NX₁ описуємо малі дуги овала. Побудовані чотири дуги обводимо суцільною лінією. Маємо наближену побудову еліпса – овал з центром у точці A.

Щоб забезпечити більшу наочність зображення, прийнято розташовувати  тіла в просторі перед вертикальною площиною так, щоб вісь кожного з них була паралельна вертикальній площині. У цьому випадку осьовий переріз циліндра або конуса буде зображатися без спотворень, а велика вісь еліпса, що зображає основу, буде перпендикулярна до зображення осі циліндра чи конуса. На практиці для зображення циліндра проводять вертикальну пряму, на ній довільно відмічають проєкції центрів основ циліндра. За допомогою шаблона еліпса зображають основи циліндра, розміщуючи еліпс так, щоб його центр співпадав з відміченими точками,  а мала вісь еліпса лежала вздовж проєкції осі циліндра. З’єднавши відрізками відповідні кінці великих осей еліпсів, що зображають основи, одержимо зображення крайніх видимих (контурних) твірних циліндра. Контурні твірні ділять бічну поверхню циліндра на дві рівні частини: видиму (при погляді спереду) і невидиму.

   Якщо при розв’язуванні задачі потрібно розглянути осьовий переріз циліндра, то рекомендується побудувати його під деяким кутом до фронтального осьового перерізу. Це надасть зображенню більшої об’ємності.

   Будуючи наочне зображення конуса, учні часто допускають помилки.

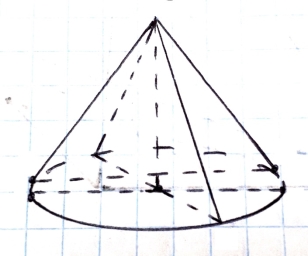
   Одна з них полягає в тому, що вони сполучають відрізком прямої вершину конуса з кінцями великої осі еліпса. Вважають твірні SB і SA контурними. Причиною цієї помилки є те, що учні розглядають конус як геометричне тіло, утворене обертанням прямокутного трикутника SOA навколо катета SO. При цьому SA вважають контурною твірною. Але контурна твірна не може проходити через точку А. Тоді б вона була перпендикулярна до АВ. Але прямі ОА і SC в оригіналі є мимобіжними.

Інша помилка учнів – кут CSD вважають кутом осьового перерізу конуса. Але хорда CD не проходить через центр основи конуса, а тому переріз SCD не проходить через висоту конуса. Щоб уникнути цієї помилки, треба провести інший діаметр основи конуса і його кінці з’єднати з вершиною S. На малюнку осьовим перерізом є трикутник SMN.

   При зображенні конуса проводять вертикальну пряму, відмічають на ній зображення центра основи і вершини конуса. За допомогою шаблона еліпса креслять основу конуса. Потім із точки, що є проєкцією вершини конуса, проводять дві дотичні до еліпса. Вони зображатимуть контурні твірні конуса. На відміну від циліндра, контурні твірні конуса не ділять його бічну поверхню на дві рівні частини. Це було би можливо тоді, коли б проєктуючі прямі були паралельні до площини основи конуса. Але тоді основа зображалася б відрізком, а не еліпсом. 

   У всіх випадках, коли конус розташований вершиною вверх, а його основа не проєктується у відрізок, видимою залишається більша частина бічної поверхні. Коли конус розміщений вершиною вниз, то видимою буде менша частина бічної поверхні. В обох випадках переріз, що проходить через контурні твірні не є осьовим. Осьовий переріз потрібно будувати так, щоб він не проходив через жодну з контурних твірних.

   Куля зображається у вигляді круга. Коло цього круга зображає велике коло сфери, що обмежує цю кулю. Якщо на кресленні позначити кулю лише її обрисом у вигляді кола, то таке зображення не створить наглядного образу кулі як геометричного тіла.

Тому рисунок доповнюється ще одним перерізом, перпендикулярним до площини зображення, який проходить через центр кулі. Цей переріз називається великим кругом.

   Таким чином, незважаючи на прагнення вчителя скоротити затрати часу на уроках  шляхом використання готових малюнків, виконаних наперед за допомогою сучасних технічних засобів чи таблиць, систематично ігнорувати традиційний рисунок на класній дошці та в учнівських зошитах є недоречно, тому що учні не бачать процесу побудови зображення. Щоб сформувати необхідні вміння, учні самі повинні виконувати рисунки в зошитах. Слідкуючи за тим, в якій послідовності та як проводить лінії вчитель, коли і як використовує креслярські інструменти, учні набувають навичок креслярського мистецтва.

   Оскільки зображення фігури є допоміжним етапом розв’язування задачі, то необхідно прагнути виробити в учнів навички виконання малюнків від руки, без креслярських інструментів. Для цього корисно скласти і запам’ятати алгоритм побудови зображень найбільш вживаних фігур на аркушах в клітинку.

Література

1.Я.М. Жовнір. Позиційні задачі з стереометрії.- Київ, «Освіта», 1991р.

2.Я.Е.Гольдберг. С чего начинается решение стереометрической  задачи.- Київ, «Радянська школа», 1990 р.

3.Н.М.Повзло. Проблеми розв'язування стереометричних задач та пояснення їх розв'язання.- Харків, видавнича група «Основа»,  математика в школах України, №8, 2009 р.