Урок "Паралельність прямої та площини."

Тема. Паралельність прямої та площини.

Формування компетентностей:

• предметна компетентність:

• розглянути випадки взаємного розміщення прямої і площини;
• сформувати поняття прямої, паралельної площині;
• домогтися засвоєння ознаки паралельності прямої і площини;
• сформувати вміння розв’язувати задачі, що передбачають застосування означення та ознаки паралельності прямої і площини;

• ключові компетентності:

• спілкування державною мовою – доречно та коректно вживати в мовленні математичну термінологію;
• інформаційно-цифрова компетентність – визначати достатність даних для розв’язування задач;
• соціальна та громадянська компетентності – оцінювати аргументи та змінювати думку на основі доказів.

 

Тип уроку: комбінований.

Обладнання та наочність: моделі: куб, піраміда, площини із прямими, комп’ютер, проектор, екран, креслярські приладдя, презентація «Паралельність прямої та площини», картки-завдання на два варіанти, підручник Г. П. Бевз «Математика» 10 клас, рівень стандарту, 2018р.

Хід уроку

1. Організаційний етап

Перевірка готовності учнів до уроку, налаштування на роботу.

2. Перевірка домашнього завдання.

1. Перевірка завдання, заданого за підручником.

2. Виконання завдань картки № 1, №2 (6 учнів)

Картка № 1

1. Дві прямі лежать в одній площині і не перетинаються називаються …

А) паралельними; Б) мимобіжними; В)  збігаються; Г) перетинаються.

2. Дві прямі k і  l паралельні прямій m. Укажіть взаємне розміщення прямих k і l.  

А) Мимобіжні;   Б) паралельні;      В) перетинаються; Г) паралельні або мимобіжні.

3. Укажіть, скільки площин можна провести через діагональ куба та його ребро

А) жодної; Б)  тільки одну; В) жодної або нескінчену множину; Г) жодну або одну.

 

 

 

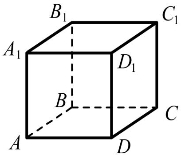 На рисунку зображено куб АBCDA₁B₁C₁D₁. Установіть відповідність між парами прямих (1 – 3) і співвідношеннями між ними (А – Г)

 

1	AB  і AA1	А	паралельні
2	AB і C1D1	Б	перетинаються
3	AB і B1C1	В	мимобіжні
		Г	збігаються

 

4. Через кінці відрізка АВ і його середину М проведено паралельні прямі, які перетинають площину α в точках А₁, В₁, М₁ відповідно. Знайти довжину відрізка ММ₁, якщо АА₁=10см, ВВ₁=12см і відрізок АВ не перетинає площину α.
5. Через кінець А відрізка АВ проведено площину . Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину відповідно в точках В₁ і С₁. Знайти довжину відрізка СС₁, якщо АВ:ВС=4:1, ВВ₁=8см.

 

Картка №2

1.  Дві прямі, які не лежать в одній площині називаються …

А) паралельними; Б) мимобіжними; В)  збігаються; Г) перетинаються.

2.   Прямі m і n перетинаються, а пряма d паралельна прямій n. Укажіть можливе взаємне розміщення прямої m по відношенню до d.

А) мимобіжні;  Б) паралельні;    В) перетинаються; Г)  збігаються.

3. Укажіть, скільки площин можна провести через діагональ куба та діагональ його грані

А) жодної;  Б) тільки одну;  В) жодної або нескінчену множину; Г) жодну або одну.

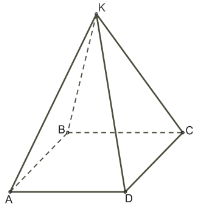4.     На рисунку зображено піраміду АBCDК. Установіть відповідність між парами прямих (1 – 3) і співвідношеннями між ними (А – Г)

 

 

1	AB  і КD	А	паралельні
2	AB і DС	Б	перетинаються
3	AB і BК	В	мимобіжні
		Г	збігаються

 

 

5. Через кінці відрізка АВ і його середину М проведено паралельні прямі, які перетинають площину α в точках А₁, В₁, М₁ відповідно. Знайти довжину відрізка ММ₁, якщо АА₁=20см, ВВ₁=24см і відрізок АВ не перетинає площину α.
6. Через кінець А відрізка АВ проведено площину . Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають площину відповідно в точках В₁ і С₁. Знайти довжину відрізка ВВ₁, якщо АВ:ВС=4:1, СС₁=9см.

 

3. Актуалізація і корекція опорних знань.

Інтерактивна гра: «Незакінчене речення» Слайд 2-3.

1. Основні поняття стереометрії: точка, пряма і …..площина.

2. Твердження, які доводять, називають…теоремами.

3. Якщо пряма і площина мають тільки одну спільну точку то вони ….перетинаються.

4. Якщо через пряму проходять дві різні площини, то площини …. перетинаються по прямій.

5. Якщо дві точки прямої належать площині, то і вся пряма цій площині … належить.

6. Через будь-якій три точки, які не лежать на одній прямій, можна провести площину і до того ж тільки ….одну.

7. Дві прямі, які не лежать в одній площині, називають….. мимобіжними.

8. Через дві прямі, що перетинаються провести ….. площину і до того ж тільки одну.

9. Дві прямі лежать в одній площині і не перетинаються називають…паралельними.

10.  Площину однозначно визначають пряма і точка, що не лежить на цій….прямій.

11.  Якщо одна пряма лежить у деякій площині , а друга перетинає цю площину в точці, що не належить першій прямій, то такі дві прямі … мимобіжні.

12.  Через будь-яку точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній і до того ж тільки ….одну.

13. Дві прямі, паралельні третій паралельні ….. між собою.

14.  Скільки площин можна провести через три точки, що лежать на одній площині…. безліч.

15. Колії залізничної дороги між собою….паралельні.

16. Середніх ліній в трикутнику можна провести…три.

4. Мотивація навчальної діяльності. (Слайд 4-8)

Кожен раз, коли ми приходимо в ліцей ми бачимо навчальний корпус, ялинку, асфальт на якому зроблена розмітка. Виникає у мене і у вас запитання: як розміщені ці предмети між собою і що вони мають спільного між собою? На ці запитання відповість  геометрія. Ялинка в нас струнка, як пряма, стіна є площина. Отже, розглянемо, як можуть бути розміщені між собою прямі і площини у просторі.

 

5. Повідомлення теми, мети, завдань уроку і мотивація навчальної діяльності. (Слайд 9)

Тема. Паралельність прямої та площини.

План

1. Взаємне розміщення прямої і площини в просторі.
2. Означення паралельних прямої та площини.
3. Ознака паралельності прямої та площини.
4. Розв’язування задач.

6. Сприймання й усвідомлення учнями фактичного матеріалу.

1. Взаємне розміщення прямої і площини в просторі. (Слайд 10)

 

 

 

 

 

 

 

 

Пряма лежить у площині (кожна точка прямої належать  площині) (Слайд 11)

(Мал. 1 )

 

 

m ⸦ α

Пряма перетинає площину (пряма і площина мають одну спільну точку) Слайд 12 (Мал. 2 )                                                                         p

    

                                                         р

 

р ∩ β = А

Пряма паралельна площині( пряма і площина не мають жодної спільної точки) Слайд 14

   (Мал. 3)       d

 

 

 

 

 

 

d ∩ ω =  ?    то   d ||  ω

2. Означення.

Пряму і площину називають паралельними, якщо вони не мають спільних точок

 

3. Властивості паралельних прямої і площини

Теорема (Ознака паралельності прямої і площини) Слайд 14.

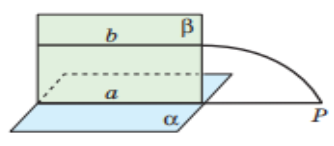Якщо пряма паралельна якій-небудь прямій площини, то вона паралельна і самій площині.

Дано.

 b||a і a ⸦ α .

Довести

 b||α.

Доведення.

Припустимо, що пряма b не паралельна α,  а перетинає площину α у деякій точці Р (Мал.4 ). Ця точка лежить у площині α і площині β, яка проходить через паралельні прямі a і b. Отже, точка Р лежить на прямій a, по якій перетинаються площини α і β. Прийшли до суперечності: прямі a і b мають спільну точку Р. Виходить, що пряма b не може перетинати площину α. Вона і не лежить у площині α. Отже, b||α.

Теорема Слайд 15

Якщо площина проходить через пряму, паралельну другій площині, і перетинається з цією площиною, то пряма їх перетину паралельна даній прямій.

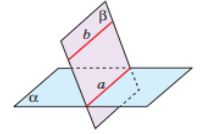Дано

b || α, b ⸦ β, α ∩ β = a 

Довести

 a||b.

 

Доведення

Якби прямі a і b перетиналися, точка їх перетину була б спільною для прямої b і площини α. Це неможливо, оскільки b || α. Отже, прямі a і b не перетинаються. А лежать вони в одній площині β. Тому a||b. Якщо b ⸦ α, то теорема очевидна.

Інформаційне повідомлення

Одним із українських математиків є наш земляк Микола Андрійович Чайковський. (Слайд 16)  Народився 2 січня 1887 року в м. Бережани. Закінчивши бережанську гімназію, вчився у Віденському університеті і завершив навчання у Львівському університеті. В 1911 році у Відні М. Чайковський здобув ступінь доктора філософії. З 1918 року працював доцентом у Кам’янець - Подільському університеті, а пізніше в Одеському університеті. Однак у березні 1933 року його арештували. Перебував в таборах Гулагу до 1943 року.

Слід відзначити, що Микола Чайковський – єдиний галичанин, який пройшов „Біломор” і Соловки, вижив і повернувся до Львова, де продовжував працювати. Його  вислів «Я можу з великою гордістю сказати, що був другим, хто викладав вищу математику українською мовою; першим був Михайло Пилипович Кравчук у Києві…                                                                                                                            М. Чайковський

Він працював над словником математичних термінів українською мовою. Ось деякі репресовані терміни: (Слайд 17)

пряма - проста

паралельні прямі - рівнобіжні прості

прямі, що перетинаються - перехресні прості

перпендикулярні прямі – сторчові прямі

відрізок – відтинок

VII. Формування первинних умінь.

Виконання усних вправ.

№ 934 (Слайд 18)

Пряма a паралельна площині α. а) Чи кожна пряма площини паралельна прямій a? б) Скільки в площині α можна провести прямих, паралельних прямій a? в) Чи існують у площині α прямі, мимобіжні з прямою a?

Розв’язання

а) Ні, не кожна пряма площини α паралельна прямій a .

б) В площині α можна провести безліч прямих, паралельних прямій a.

в) Так, у площині α існують прямі, мимобіжні з прямою а.

№ 936 (Слайд 19)

Кожна з прямих а і b паралельна площині α. Чи випливає з цього, що прямі   а і b паралельні?

Розв’язання

Якщо a||α і b||α, то з цього не випливає, що a||b ( а і b можуть перетинатися або бути мимобіжними ).

Виконання письмових вправ

№ 941 (Слайд 20)

АВСD - паралелограм. Площина ω проходить через його вершини A, B і не проходить через вершину C. Доведіть, що CD || ω.

Розв’язання                                                                      D                          С

Дано

АВСD – паралелограм

А є  ω, В є ω.

Довести

CD || ω.

Розв’язання

Оскільки А є  ω, В є ω то за аксіомою С₃ то пряма АВ ⸦ ω. СD || АВ (за означенням паралелограма), то за ознакою паралельності прямої і площини

CD || ω.  Отже, задача доведена.

№ 941 (Слайд 21)

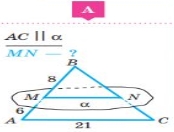Розв’яжіть задачі за готовими малюнками 234 (А).

        Розв’язання

      АС || α, МN|| АС 

Розглянемо Δ АВС і Δ МВN,

 < В – спільний,   < А = < М, <С = < N, то

 Δ АВС ~ Δ МВN.  АВ = 6 + 8 = 14

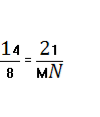  МN =

           Відповідь 12.

 

№ 949.

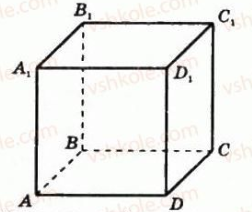Яким граням прямокутного паралелепіпеда ABCDA₁B₁C₁D₁ паралельна пряма: а) AB; б) B₁C₁; в) DD₁? Слайд 22

Розв’язання

а) AB || DD₁С₁С, AB || А₁В₁С₁D₁;

б) B₁C₁  || АВСD, B₁C₁  || АА₁D₁D;

в) DD₁ || ВВ₁С₁С, DD₁ || АА₁В₁В

 

 

№ 953.

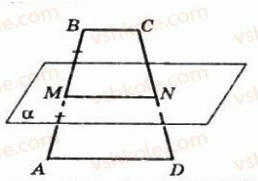Площина α, паралельна основі трапеції, перетинає її бічні сторони AB і CD у точках M і N відповідно. Знайдіть MN, якщо AD = 7 см, BC = 3 см, а AM = BM.

Дано

АВСD – трапеція, α || ВС || АD

АВ ∩ α = М, СD ∩ α = N

AD = 7 см, BC = 3 см,  AM = BM

Знайти  МN.

Розв’язання

Оскільки α || ВС || АD то  МN || АD.

За умовою AM = BM, тоді за теоремою Фалеса

СN = ND. Отже, NM – середня лінія трапеції АВСD.

       Відповідь 5 см.

 VII . Підсумки уроку.

Інтерактивна гра «Скачки на конях», створена за допомогою онлайнового сервісу Learningapps. Посилання: https://learningapps.org/6010988 (Слайд 23)

Перегляд відеопрезентації, створеної учнем «Паралельність прямої і площини у нашому » (Слайд 24)

 

 VIII.  Домашнє завдання. (Слайд 25)

Вивчити §26  розділ 4 (підручник Г. П. Бевз «Математика» 2018р.)

Вправи: № 944, 947 (Б) і  додатково

Створити презентацію «Взаємне розміщення прямої і площини навколо нас»

IX.  Рефлексія.

Для взаємозв′язку вчителя з учнями використовується прийом «Скринька побажань».

Що сподобалось на уроці ? Що не сподобалось?        Що пропонуєш змінити?

Учні пишуть відповіді на зелених аркушах і кладуть до скриньки.

Завершити наш урок я б хотіла словами: «Якщо ви хочете, щоб життя посміхалося вам, подаруйте йому спочатку свій гарний настрій і знання».

Дякую вам за урок. Бажаю всім успіхів і гарного настрою!