Методичні рекомендації до вивчення розділу «Кінематика».
Методичні рекомендації до вивчення розділу «Кінематика»
Одним із шляхів оновлення змісту освіти й узгодження його із сучасними потребами, інтеграцією до європейського та світового просторів є орієнтація на формування компетентностей та створення ефективних механізмів їх упровадження.
Мета навчання предметів природничо-математичного циклу полягає у формуванні засобами навчальних предметів ключових компетентностей учнів, необхідних для соціалізації, творчої самореалізації особистості, розуміння природничо-наукової картини світу, вироблення екологічного стилю мислення і поведінки, розвитку експериментальних умінь і дослідницьких навичок та виховання громадянина демократичного суспільства.
До цих предметів належить один із найскладніших – фізика. Фізика є важливою складовою загальноосвітньої підготовки. Місце фізики в системі загальної середньої освіти визначається її роллю в інтелектуальному, соціальному і моральному розвитку особистості, розумінні будови і використання сучасної техніки, нових інформаційних технологій, сприйманні наукових і технічних ідей, формуванні наукової картини світу і сучасного світогляду. Фізика є опорним предметом при вивченні суміжних предметів (хімії, інформатики, біології, географії), тому без належної підготовки з цього предмета неможлива повноцінна освіта сучасної людини.
Учні мають засвоїти зміст навчального матеріалу, опанувати наукові факти i фундаментальні iдеї, усвiдомити суть понять i законiв, принципiв i теорiй, якi дають змогу пояснити перебiг фiзичних явищ i процесiв, з’ясувати їхнi закономiрностi, характеризувати сучасну фiзичну картину свiту, зрозумiти науковi основи сучасного виробництва, технiки i технологiй, оволодiти основними методами наукового пiзнання i використати набутi знання в практичнiй дiяльностi.
До ПТНЗ будівельного профілю, в тому числі до Київського професійного будівельного коледжу, вступають учні, близько 50% яких не знають таблиці множення, не володіють арифметичними діями і не вміють навіть виконувати елементарні дії за допомогою калькулятора. Школа навчає всіх, але ми бачимо, що навчити всіх вона не може. Наші абітурієнти мають в основному рівень навчальних досягнень – «середній».
Такі учні, як підтверджує мій досвід та досвід моїх колег, відстають у навчанні, оскільки не вміють працювати з підручниками, довідниками, не цікавляться науково-популярною літературою, а дехто навіть не вміє читати. Біля 60% наших учнів не бажають вивчати предмети, що безпосередньо не стосуються оволодіння обраної ними професії.
І саме з таких учнів викладачі ПТНЗ повинні готувати робітників нового покоління, новаторів, інтелектуальну робітничу еліту, тих, хто впливатиме на життя держави в найближчий час та у віддаленому майбутньому. Ми повинні підготувати учня до життя й праці у надзвичайно швидкозмінному світі, створити умови для всебічного розвитку учня, сформувати високоосвічену, професійно спрямовану особистість, здатну знайти своє місце в складних умовах життєвих реалій.
Отже, саме життя вимагає нового підходу до методики викладання фізики таким учням. Курс фізики потрібно максимально наблизити до професії, яку здобувають учні. Вчитель повинен перш за все зацікавити учнів своїм предметом. Якщо викладач хоче, щоб учні вивчали його предмет, він повинен звернути увагу на мотивацію учня, розкривати не лише кінцеву мету вивчення фізики, а й важливість вивчення конкретної теми, розділу для їх майбутньої професії.
Труднощі при розвя’зуванні задач y вивченнi фізики поглиблються ще й тому, що учні не достатньо засвоюють одиниці метричних мір, особливо співвідношення між одиницями об’єму і одиницями площі. Зовсім погано вони оперують такими одиницями, як літр, мілілітр. Дуже часто можна почути: ”літр це - кілограм”.
На мій погляд, щоб зменшити проблеми у розв’язуванні задач потрібно приділяти велику увагу й високі вимоги до вибору задач. Насамперед, задачі повині мати дослідницький, а не формальний характер, бути не абстрактними, а якомога ближче до життя. Приділяти більше уваги індивідуальному розв’язуванню задач з фізики. Краще розв’язати задач менше, але більш якісніше.
У нашому навчальному закладі викладачі природничо-математичних дисциплін працюють у тісному взаємозв'язку з викладачами професійно-теоретичної підготовки. У групах учнів, що здобувають професію «Слюсар з ремонту колісних транспортних засобів», ми разом складаємо наші поурочно-тематичні плани, і я бачу, який саме матеріал із фізики можна пов'язати з програмою спеціальної технології, будови автомобіля.
Матеріал до вивчення розділу «Кінематика»
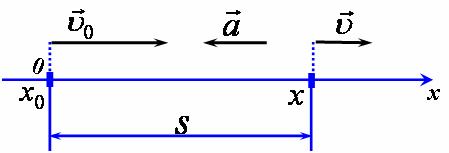
Для опису руху (зміни положення тіла в просторі з часом) необхідно мати спосіб задання просторового положення тіла і засоби вимірювання інтервалів часу. Для задання положення тіла в просторі необхідно вибрати яке-небудь матеріальне тіло (тіло відліку) і через одну з його точок (точку відліку) провести три взаємно перпендикулярні прямі (осі координат) з відкладеним масштабом для виміру відстаней. Описана сукупність зветься системою координат. Додавання до системи координат приладу для виміру часу (годинник) перетворює її в систему відліку.
Числа, за допомогою яких задається положення тіла щодо обраної системи відліку називають координатами тіла. Для задання положення різних тіл може знадобитися різне число координат. Мінімальна кількість координат, необхідна для вичерпного опису положення вільного (тобто не взаємодіючого з іншими об'єктами) тіла в просторі називається кількістю ступенів вільності цього тіла. Чим більшим числом ступенів вільності володіє тіло, тим складніше виявляється задача опису його руху. Серед макроскопічних тіл мінімальним числом ступенів вільності володіють так звані абсолютно тверді тіла. Такі тіла не деформуються та здатні переміщатися й обертатися уздовж (навколо) кожного з трьох напрямків, обумовлених осями координат і, отже, володіють шістьма ступенями вільності. При розв’язуванні багатьох задач механіки можуть виявитися малоістотними розміри розглянутого тіла, відносні переміщення його частин чи руху тіла як цілого. У цьому випадку кількість розглянутих ступенів вільності може бути штучно зменшена до трьох. У результаті реальне тіло заміняється його математичною моделлю – матеріальною точкою.
Матеріальна точка – це фізична модель тіла реальної маси, розмірами якого за даних умов руху можна знехтувати.
Опису руху у механіці може бути:
А. Словесний. Наприклад: ...щоб потрапити з мого будинку в школу треба вийти на вулицю, повернути праворуч, пройти через двір, звернути ліворуч...
Переваги: простий, не вимагає наукових знань.
Недоліки: занадто не точний, не є науковим, не дозволяє вирішити задачу механіки.
Б. Табличний. Наприклад:
Переваги: наочний, простий, зручний при вивченні періодичних рухів.
Недоліки: не дозволяє визначити положення тіла в будь-який момент часу (проміжні значення), не дозволяє передбачати характер руху.
В. Графічний. Наприклад: рис.2.2.
|
t, с |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
X, м |
0 |
1 |
3 |
4 |
6 |
2 |
1 |
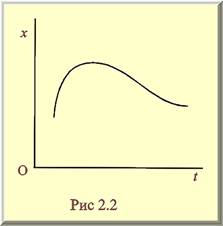 Переваги: наочний.
Переваги: наочний.
Недоліки: неточний, не можна прогнозувати характер руху надалі.
Г. Аналітичний (координатний). Наприклад:![]() , де
, де ![]() – переміщення і радіус-вектор відповідно, або
– переміщення і радіус-вектор відповідно, або
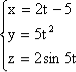 .
.
Переваги: точний, дозволяє однозначно вирішити основну задачу механіки, має можливість передбачати характер руху.
Методика розв'язування задач з кінематики
Розв'язування будь-якої фізичної задачі до певної міри може бути умовно поділене на три етапи: фізичний, математичний та аналіз розв'язку.
На фізичному етапі:
- аналізують умову задачі та опис фізичної ситуації, поданої в умові;
- з'ясовують фізичну модель явища, покладеного в основу задачі;
- репрезентують фізичну модель явища в графічній формі (малюнки, креслення, схеми, графіки тощо);
- роблять скорочений запис умови задачі у систематизованому вигляді.
На математичному етапі:
- пропонують математичну модель задачі, складають загальні рівняння, що описують фізичні явища, зазначені в умові задачі;
- визначають конкретні умови й параметри, за яких відбувається явище;
- конкретизують загальні рівняння у вигляді часткових розв'язків аналітичним, графічним або числовим способом, виконують обчислення.
На етапі аналізу розв'язку:
- проводять перевірку одиниць фізичних величин і знаходять значення шуканих величин;
- аналізують результати, їх вірогідність і реальність;
- шукають інші методи розв'язування задачі й обирають найраціональніший.
У процесі розв'язування задач кінематики головне полягає в тому, щоб за заданими параметрами руху (координати, переміщення, швидкість тощо) записати рівняння руху. Або навпаки, якщо рівняння руху відоме, шукають фізичні величини, що його описують.
Розв'язування задач кінематики підпорядковується певній послідовності розумових дій, так званому алгоритму, за допомогою якого пошук розв'язку фізичної задачі упорядковується і значно полегшується. Наведемо його як послідовність кроків, яких варто дотримуватися в процесі розв'язування задачі.
Крок 1. За даними умови задачі оберіть систему відліку, в якій буде розглядатися рух тіла. Визначте початкові значення координат, пов'язавши їх з обраним тілом відліку.
Крок 2. Визначте характер руху (рівномірний, нерівномірний) та вид траєкторії (прямолінійна, криволінійна).
Крок 3, Зробіть малюнок, який ілюструє фізичні явища, зазначені в умові задачі. Пов'яжіть малюнок з обраною системою відліку, зазначте на ньому векторні фізичні величини.
Крок 4. Побудуйте проекції переміщення, швидкості, інших векторних величин і запишіть рівняння руху тіла в загальному вигляді. У разі необхідності, якщо кількість невідомих більша, ніж кількість рівнянь, складіть додаткові рівняння, що пов'язують кінематичні величини.
Крок 5. Розв'яжіть рівняння відносно шуканих величин. Визначте їхнє значення та оцініть їхню вірогідність.
Крок 6. Проаналізуйте отриману відповідь. Якщо вона суперечить фізичному змісту задачі, шукайте нові ідеї щодо її розв'язання.
Крок 7. Здійсніть пошук інших можливих шляхів розв'язування даної задачі. Розв'яжіть задачу кількома способами і порівняйте результати. Оцініть, який з розв'язків найраціональніший.
Задача. З пунктів А і В, розташованих на відстані 80 км один від одного, одночасно почали рух назустріч два велосипедисти. Перший мав швидкість 5 м/с, другий 3 м/с. Визначити:
1) через який час вони зустрінуться і де це відбудеться;
- який шлях вони пройдуть до моменту зустрічі та яке здійснять переміщення;
- через який час від початку руху відстань між ними буде 20 км.
Розв'язання
 1. Оберемо систему відліку таким чином, щоб початок коор-
1. Оберемо систему відліку таким чином, щоб початок коор-
динат збігався з пунктом А. У загальній формі рівняння руху
тіла має такий вигляд: ![]() . Запишемо тепер його для
. Запишемо тепер його для
кожного з велосипедистів окремо. Оскільки для першого вело-
сипедиста початкова координата ![]() дорівнює 0, проекція швидкості
дорівнює 0, проекція швидкості ![]() , а її модуль дорівнює за умовою 5 м/с, то рівняння руху матиме вигляд:
, а її модуль дорівнює за умовою 5 м/с, то рівняння руху матиме вигляд: ![]() .
.
Для другого велосипедиста ![]() км,
км, ![]() ,
, ![]() м/с,
м/с, ![]() .
.
Унаслідок руху з плином часу координати обох тіл змінюються: у першого вона зростає, у другого - зменшується. У момент їх зустрічі координати обох велосипедистів збігаються: ![]() . Підставивши відповідні рівняння руху, одержимо рівняння з одним невідомим:
. Підставивши відповідні рівняння руху, одержимо рівняння з одним невідомим:
![]() ;
; ![]() ; звідси
; звідси ![]() с = 2,8 год.
с = 2,8 год.
Отже, велосипедисти зустрінуться через 2,8 год. Місце їх зустрічі визначать координати х1 і х2, які можна знайти з рівняння руху кожного з тіл, підставивши в нього час ![]() :
:
а) ![]() = 5 м/с • 10 000 с = 50 000 м = 50 км;
= 5 м/с • 10 000 с = 50 000 м = 50 км;
б)![]() = 80 000 м - 3 м/с • 10 000 с = 50000м = 50 км.
= 80 000 м - 3 м/с • 10 000 с = 50000м = 50 км.
2. Оскільки велосипедисти рухалися прямолінійно і не змінювали напряму руху, то пройдений ними шлях дорівнюватиме
модулю переміщення (або його проекції):
![]()
![]() ;
; ![]() ,
, ![]() .
. ![]()
Або ![]() * 10000с=30000 м=30км.
* 10000с=30000 м=30км.
3. Щоб знайти час, коли відстань між тілами дорівнюватиме
20 км, достатньо записати рівності ![]() = 20 км або
= 20 км або ![]()
= 20 км та підставити в них відповідні рівняння руху велосипедистів.
![]() .
. ![]() .
. ![]()
![]() .
. ![]() .
. ![]()
Чим можна пояснити дві різні відповіді? Якщо проаналізувати умову задачі, то можна помітити, що на відстані 20 км один від одного велосипедисти будуть двічі - коли їдуть назустріч один одному (2,1 год) і коли роз'їжджаються після зустрічі, продовжуючи рух (3,5 год).
Правила розв’язування задач з кінематики
1.Зробити схематичний малюнок, на якому показати траєкторію руху точки і вибрану систему відліку.
2. Визначити вид руху вздовж кожної з координатних осей.
3.Для кожної осі показати на малюнку всі кінематичні характеристики руху: початкову швидкість, прискорення, кінцеву швидкість, переміщення.
4.Записати кінематичний закон руху у векторній формі і в проекціях на вибрані осі координат.
5.Розв’язати отриману систему рівнянь і знайти шукану величину.
Методика розв’язування графічних задач з кінематики
Для розв’язування графічних задач треба знати графіки найпростіших елементарних функцій і вміти їх досліджувати.
Треба навчитися:
1)читати графіки;
2)графічно представляти умову задачі для наступного визначення за графіком певної фізичної величини;
3)за графіком залежності однієї фізичної величини від іншої будувати графіки залежностей між іншими фізичними величинами.
Зверніть увагу на те, що залежність координати і переміщення від часу у рівноприскореному русі квадратична. Формули координати переміщення для такого руху – це квадратичні функції, графіками яких будуть параболи.
![]() (1) квадратична функція
(1) квадратична функція
 квадратичні функції /
квадратичні функції /
З математики відомо, що, якщо a>0 (див. формулу (1)), то вітки параболи спрямовані угору, а якщо a <0, то вниз.
Для переміщення і координати це означає, що, якщо проекція прискорення aх >0, то вітки параболи будуть спрямовані угору, а якщо aх <0, то вниз.
Для побудови графіка треба спочатку визначити, яким значенням t відповідає S =0 або x =0.
Таким чином можна знайти і час, якому відповідає вершина параболи. Якщо t =0, то Sx =0 і x = x0 .
Методика розв’язування задач на закон додавання швидкостей і переміщень
Зверніть увагу:
1) Швидкості, переміщення, координати для одного й того самого тіла різні у різних системах відліку.
2) Не залежать від вибору системи відліку тільки час t прискорення a.
3) При розв’язуванні задач з кінематики треба всі фізичні величини,які входять в певні кінематичні рівняння, брати в одній системі відліку (СВ).
4) Перехід від однієї СВ до іншої здійснюється за допомогою закону додавання швидкостей.
Правила розв’язування задач на закон додавання швидкостей
1. Зробити схематичний малюнок, на якому показати задані тіла і швидкості їх руху.
2. З’ясувати, рух якого тіла буде розглядатися в дані й задачі.
3. Вибрати тіла, відносно яких буде розглядатися рух даного тіла, і зв’язати з ними нерухому і рухому системи відліку.
4. Швидкостям, що показані на малюнку, присвоїти буквені індекси.
5. З’ ясувати, в якій системі відліку раціональніше розв’язувати задачу.
6. У вибраній системі відліку записати у векторній і скалярній формі необхідні кінематичні рівняння, з яких можна знайти шукану величину.
7. Записати закон додавання швидкостей у векторній формі і в проекціях на вибрані осі координат. Якщо вектори швидкостей направлені під кутом один до одного, то дозволяється геометричне розв’язання одержаного трикутника швидкостей.
8. Розв’язати всі одержані рівняння і знайти шукану величину.
Приклади задач рівномірного руху
 Задача 1
Задача 1
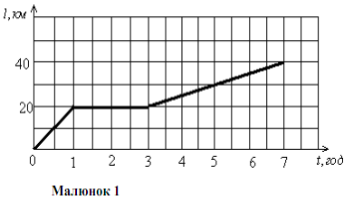
Наприклад, нехай нам відомий графік рівномірного руху тіла (малюнок 1).
За допомогою цього графіка ми можемо одержати певні відомості про рух тіла. За 1 годину тіло проїхало 20 км, потім 2 години тіло стояло, а потім за 4години тіло проїхало 20 км. При цьому за графіком ми можемо визначити й швидкість руху:
![]() 20км/ год,
20км/ год, ![]() ,
, ![]() 5км/ год.
5км/ год.
 Задача 2
Задача 2
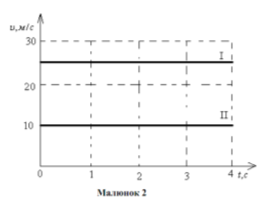
Поряд із графіками руху часто користуються графіками швидкості (малюнок 2). Для побудови графіка швидкості застосовують прямокутну систему координат, по горизонтальній осі якої відкладають у певному масштабі час, а по вертикальній – модуль швидкості.
Із цього графіка можна визначити, що швидкість першого тіла 25км/с, а другого - 10м/с.
Задача 3
Поїзд їхав 2год зі швидкістю 50км/год, потім 0,5години не рухався, потім їхав 1год зі швидкістю 100км/год. Побудуйте графіки залежності пройденого шляху та швидкості від часу.
Розв’язання:
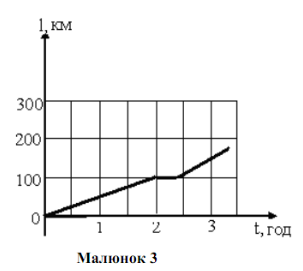 Графік залежності шляху від часу являє собою ламану (малюнок 3), оскільки на кожному з етапів руху швидкість поїзду стала. Кожний відрізок ламаної можна побудувати за двома точками. Наприклад, за перші 2 години поїзд проїхав 100км, тому, якщо вимірювати час в годинах, а відстань у кілометрах, координати кінців відповідного відрізка (0; 0) і (2; 100)
Графік залежності шляху від часу являє собою ламану (малюнок 3), оскільки на кожному з етапів руху швидкість поїзду стала. Кожний відрізок ламаної можна побудувати за двома точками. Наприклад, за перші 2 години поїзд проїхав 100км, тому, якщо вимірювати час в годинах, а відстань у кілометрах, координати кінців відповідного відрізка (0; 0) і (2; 100)
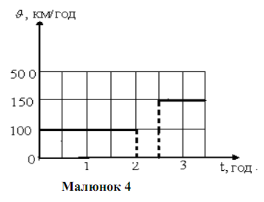 Весь час руху розіб’ємо на проміжки, протягом яких поїзд рухався рівномірно. На кожному такому проміжку графік залежності швидкості від часу є відрізком, паралельним осі t (малюнок 4).
Весь час руху розіб’ємо на проміжки, протягом яких поїзд рухався рівномірно. На кожному такому проміжку графік залежності швидкості від часу є відрізком, паралельним осі t (малюнок 4).
Задача 4
Розглянемо тепер, чим відрізняються графік залежності шляху від часу для тіл, які рухаються з різною швидкістю.
Із селища одночасно виїхали велосипедист і автомобіль. Швидкість велосипедиста 20 км/год, а швидкість автомобіля 60 км/год. Побудуємо графіки залежності шляху від часу.
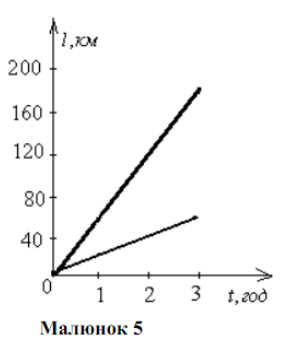 Побудуймо спочатку точки графіків, що відповідають шляху, який пройшли велосипедист і автомобіль за 1 годину. Провівши відрізки через початок координат і ці точки, дістаємо шукані графіки (малюнок 5).
Побудуймо спочатку точки графіків, що відповідають шляху, який пройшли велосипедист і автомобіль за 1 годину. Провівши відрізки через початок координат і ці точки, дістаємо шукані графіки (малюнок 5).
Потрібно звернути увагу, що графік для автомобіля нахилений під більшим кутом до осі t , ніж графік для велосипедиста, тому, що за той самий час автомобіль долає більший шлях.
Отже, що більша швидкість тіла, то більший кут між графіком залежності шляху від часу та віссю часу.
Використовуючи графіки залежності шляху від часу, розв’яжемо таку задачу.
Із селища виїхав велосипедист зі швидкістю 20 км/год, а через 4 год по тому – автомобіль зі швидкістю 60 км/год. через який час після свого виїзду автомобіль дожене велосипедиста?
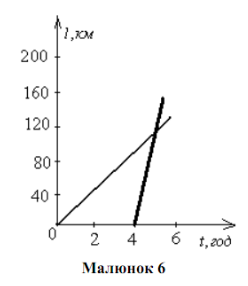 Розв’яжемо задачу графічно. Почнімо відлік часу від моменту для велосипедиста. Графік залежності шляху від часу для велосипедиста і автомобіля зображено на малюнку 6.
Розв’яжемо задачу графічно. Почнімо відлік часу від моменту для велосипедиста. Графік залежності шляху від часу для велосипедиста і автомобіля зображено на малюнку 6.
Графік залежності шляху від часу для автомобіля є також відрізком прямої, але він не проходить через початок координат, тому що автомобіль почав рухатися через 4години після початку відліку часу . Для побудови цього графіка виберемо дві точки: точку, що відповідає початку руху автомобіля. Графіки перетинаються при t = 6год, відраховуючи від моменту виїзду велосипедиста, тобто через 2години після виїзду автомобіля.
Задача 5
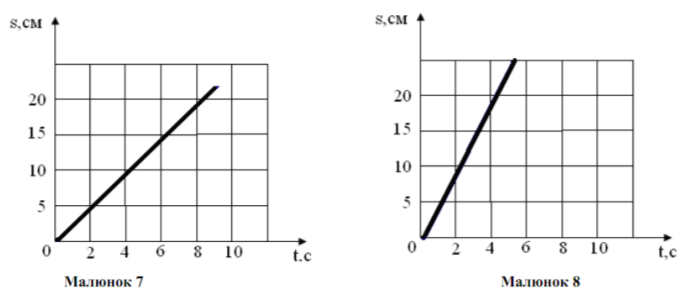
Автомобіль рухається зі сходу на захід зі швидкістю 20 м/с. Зобразити цю швидкість графічно (малюнок 7).
Розв’язуємо задачу в кілька етапів.
а) Визначаємо на папері напрям схід – захід. Позначаємо рухоме тіло точкою А і від неї проводимо промінь схід – захід.
б) Обираємо такий масштаб: відрізок завдовжки 1см відповідає швидкості 5 м/с.
в) Відкладаємо на промені чотири відрізки по одному сантиметру і ставимо стрілку у напрямі руху точки А. Від різок АВ відповідає швидкості ![]() 20 м/c .
20 м/c .
У фізиці й техніці часто доводиться розв’язувати обернену задачу: визначати пройдений тілом шлях, коли відомі час та швидкість його руху. Для цього користуються формулою для обчислення швидкості, провівши над нею математичні операції.
Скориставшись властивостями відношення, із формули швидкості ![]() , матимемо формулу шляху:
, матимемо формулу шляху: ![]() .
.
Отже, шлях, пройдений тілом, пропорційний часу. Така залежність на графіку зображається прямою лінією. На малюнку 8, показано залежність шляху від часу під час руху стальної кульки у густій рідині. З графіка можна дізнатися, що через кожні 2с шлях, пройдений кулькою, збільшувався на 5 см, тобто швидкість руху кульки
![]() ;
; ![]() = 2,5
= 2,5 ![]() .
.
або ![]() 2,5
2,5 ![]() .
.
Отже, швидкість такого руху не змінюється з часом. Рух, швидкість якого з часом не змінюється, називають рівномірним. Під час рівномірного руху тіло за будь – які однакові проміжки часу проходить однакові шляхи.
На малюнку 8 показано графік шляху, пройденого кулькою за кожні 2с вона проходить 10 см. Швидкість руху кульки ![]()
За нахилом графіка руху можна оцінювати швидкість тіла або порівнювати швидкості різних тіл: чим більша швидкість, тим графік руху крутіший.
Дії (лінійні) над векторами.
В 8-му класі ми з вами розглядали додавання, віднімання колінеарних векторів і множення вектора на скаляр. Сьогодні ми розглянемо ці ж дії над векторами, але вже не для вузького класу колінеарних векторів, а в загальному випадку.
1)Множення вектора на скаляр. Нехай задані вектор ![]() і число
і число ![]() . Добутком
. Добутком ![]() називається вектор, довжина якого дорівнює
називається вектор, довжина якого дорівнює ![]() , а напрям збігається з напрямом
, а напрям збігається з напрямом![]() , якщо
, якщо ![]() >0 і протилежний
>0 і протилежний ![]() , якщо
, якщо ![]() <0.
<0.
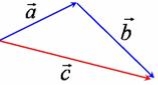
2)Додавання векторів.
|
Припустимо, ми маємо два довільних вектори
|
|
|
Правило трикутника |
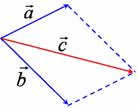
Правило паралелограма |
|
|
|
|
Сумою ( |
Сумою ( |
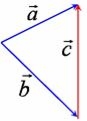
3)Віднімання векторів
Віднімання векторі є діє обернена додаванню. Різницею векторів (![]() -
-![]() ) називають вектор
) називають вектор ![]() , який потрібно додати до
, який потрібно додати до ![]() , щоб отримати
, щоб отримати ![]() . Віднімання векторів (
. Віднімання векторів (![]() -
-![]() ) теж може здійснюватись за двома алгоритмами:
) теж може здійснюватись за двома алгоритмами:
|
Правило віднімання 1 |
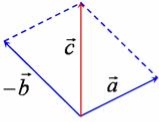
Правило віднімання 2 |
|
|
|
|
Різницею ( |
Щоб знайти різницю векторів (
( |
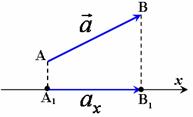
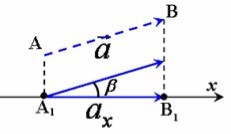
Проекція вектора на вісь
Віссю називається напрямлена пряма. Напрям прямої позначають стрілкою. Заданий на осі напрям вважають додатним, а протилежний йому - від'ємним.
Проекцією точки А на вісь х називається основа А1 перпендикуляра А А1, опущеного з точки А на дану вісь. Таким чином проекція А1 є точкою перетину осі х з площиною, яка проходить через точку А, перпендикулярно до осі х.
Проекцією вектора ![]() на вісь ОХ називають відстань між проекцією початку А1 і проекцією кінця В1 вектора на задану вісь.
на вісь ОХ називають відстань між проекцією початку А1 і проекцією кінця В1 вектора на задану вісь.
|
|
|
|
Проекція вважається додатною, якщо вектор і вісь напрямлені в одну сторону |
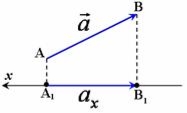
Проекція вважається від'ємною, якщо вектор і вісь напрямлені в протилежні сторони |
|
|
|
|
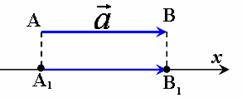
Якщо вектор паралельний до осі або повністю лежить на осі, то довжина проекції вектора дорівнює довжині самого вектора |
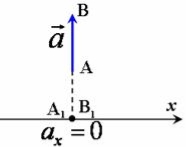
Якщо вектор перпендикулярний до осі, то його проекція на цю вісь дорівнює нулю |
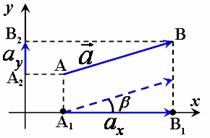
Якщо відомий кут між вектором і віссю, то проекцію можна знайти як добуток довжини вектора на косинус кута між вектором і віссю:
|
Якщо вісь одна |
Якщо є дві осі |
|
|
|
|
|
|
Властивість проекції векторів:
ØЯкщо деяка лінійна операція справедлива для векторів ![]() і
і ![]() (наприклад, сума
(наприклад, сума ![]() ), то вона справедлива і для їх проекцій на довільну, але одну і ту ж, вісь (тобто, якщо
), то вона справедлива і для їх проекцій на довільну, але одну і ту ж, вісь (тобто, якщо ![]() , то для осі ОХ:
, то для осі ОХ: ![]() ; для осі ОY:
; для осі ОY: ![]() і т.д.)
і т.д.)
КІНЕМАТИКА
Рівномірний рух: ![]() [М/с]
[М/с]
![]() ,
, ![]() ;
; ![]()
Рівноприскорений рух:
Швидкість: ![]() ,
, ![]()
Прискорення: a=const, ![]() ,
, ![]() ; [М/с2]
; [М/с2]
Шлях ![]() ,
, ![]() ; υ=
; υ=![]() 0+at ,
0+at , ![]() ;
;
Координата тіл ![]() ;
;
Падіння, рух вгору: а = g= 9,8 м/ с2, h = S
↓ h = ![]() t +
t + ![]() ↑ h =
↑ h = ![]() t -
t - ![]()
h = ![]() h =
h = ![]()
![]()
![]()
![]()
![]()
t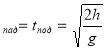 t пад = t под.=
t пад = t под.=![]()
![]() h под. =
h под. = ![]()
 Обертальний рух:
Обертальний рух:
Кутова швидкість: ![]() ,
, ![]() ,
, ![]() = 2πν
= 2πν
Частота ![]() , період Т =
, період Т =![]()
Доцентрове прискорення 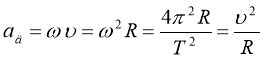 ,
,
Лінійна швидкість: υ = ![]() R = 2πRν =
R = 2πRν = ![]() =
= ![]()
Зубчате колесо: ![]() ,
, ![]() , то
, то ![]()
Задача № 1
Автомобіль, рухаючись рівносповільнено зменшив свою швидкість від 20 м/с до 15 м/с за 2 с. Знайдіть прискорення автомобіля, та шлях, пройдений ним за час гальмування.
Розв'язання:
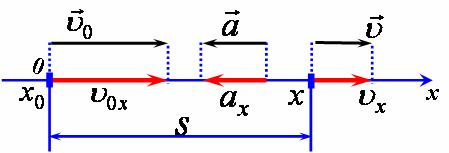
|
1) Побудуємо схему руху, пов'язавши систему відліку з землею. 2) Оскільки даний рух цілком є рівносповільненим, то він складається з однієї ділянки, яку ми опишемо, використовуючи закони рівнозмінного руху. 3) Для полегшення розв'язку задачі вважатимемо, що вісь координат ОХ напрямлена вздовж руху тіла, та в момент час t=0 тіло знаходилось в початку координат. На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення (рис 1).
Рис.1 4) Спроектуємо зазначені вектори на вісь (рис 2).
Рис.2 |
5) Запишемо рівняння руху та швидкості для даного руху в проекціях на обрану вісь ОХ:
Рівняння руху в загальному вигляді:
![]()
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
![]()
Підставимо відповідні значення в рівняння руху:
![]() (1)
(1)
Рівняння швидкості в загальному вигляді:
![]()
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
![]()
Підставимо відповідні значення в рівняння швидкості:
![]() (2)
(2)
Отримали систему рівнянь з двома невідомими s та a:
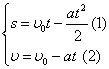
6) Розв'яжемо отриману систему рівнянь відносно шуканих невідомих:
З рівняння (2) знайдемо прискорення руху:
![]() (3)
(3)
Підставимо рівняння (3) в (1): ![]()
![]()
![]() (*)
(*)
Підставимо в отриману кінцеву формулу значення:
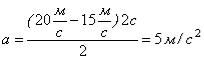
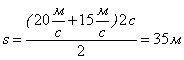
Відповідь: ![]() ;
; ![]()
Перелік задач з теми «Кінематика», які викликають захоплення учнів
 1. Користуючись рисунком, визначити місце (координату) зустрічі автомобілів, що рухаються рівномірно.
1. Користуючись рисунком, визначити місце (координату) зустрічі автомобілів, що рухаються рівномірно.
А. 0. Б. –20 км. В. 20 км. Г. –30 км.
 2. Користуючись рисунком, записати рівняння координати тіла, що рухається рівномірно.
2. Користуючись рисунком, записати рівняння координати тіла, що рухається рівномірно.
 3. Користуючись рисунком, визначити, на якій відстані один від одного будуть перебувати автомобілі, що рухаються рівномірно, через 2 год.
3. Користуючись рисунком, визначити, на якій відстані один від одного будуть перебувати автомобілі, що рухаються рівномірно, через 2 год.
А. 0. Б. 40 км. В. 20 км. Г. 60 км.
 4. Користуючись рисунком, записати рівняння залежності координати тіла від часу, якщо тіло рухається рівномірно.
4. Користуючись рисунком, записати рівняння залежності координати тіла від часу, якщо тіло рухається рівномірно.
А. х = –200 – 20t. Б. х = 200 + 20t.
В. х = –200 + 20t. Г. х = 200 – 20t.
5. Мотоцикліст їде рівноприскорено і через 5 с після початку руху розвиває швидкість 3 м/с. Визначити швидкість мотоцикліста через 10 с після початку руху.
А. 6 м/с. Б. 4,5 м/с. В. 3 м/с. Г. 8 м/с.
6. Автомобіль на мокрому шосе може гальмувати із прискоренням 2 м/с2. Обчислити гальмовий шлях автомобіля до зупинки, якщо він рухається зі швидкістю 10 м/с.
А. 5 м. Б. 25 м. В. 20 м. Г. 50 м.
7. Автомобіль їхав з пункту А в пункт В зі швидкістю 70 км/год, а повертався назад зі швидкістю 30 км/год. Визначити середню швидкість руху автомобіля.
А. 50 км/год. Б. 40 км/год. В. 42 км/год. Г. 100 км/год.
8. Під час обгону швидкість автомобіля зросла від 36 км/год до 90 км/год за 10 с. Обчислити прискорення автомобіля.
А. 5,4 м/с2. Б. 1,5 м/с2. В. 6,3 м/с2. Г. 2,7 м/с2.
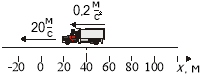 9. Користуючись рисунком, де показано положення, швидкість та прискорення тіла при t = 0, записати рівняння залежності проекції швидкості від часу, вважаючи рух рівнозмінним.
9. Користуючись рисунком, де показано положення, швидкість та прискорення тіла при t = 0, записати рівняння залежності проекції швидкості від часу, вважаючи рух рівнозмінним.
А. υх = –20t – 0,1t2. Б. υх = –20 – 0,2t.
В. υх = 40 – 20t – 0,1t2. Г. υх = 20 + 0,2t.
10. У скільки разів зросте гальмовий шлях автомобіля, якщо його швидкість збільшиться в 4 рази? Рух вважати рівнозмінним з однаковим прискоренням в обох випадках.
А. 2 рази. Б. 4 рази. В. 8 раз. Г. 16 раз.
11. Першу половину часу рейсовий автобус проїхав зі сталою швидкістю 40 км/год. З якою сталою швидкістю він повинен рухатись решту часу, якщо середня швидкість руху повинна становити 50 км/год?
А. 50 км/год. Б. 60 км/год. В. 59 км/год. Г. 90 км/год.
12. Під час аварійного гальмування автомобіль, що рухався зі швидкістю 90 км/год, зупинився через 5 с. Обчислити проекцію гальмового прискорення на напрям швидкості автомобіля.
А. 5 м/с2. Б. 18 м/с2. В. –5 м/с2. Г. –1,8 м/с2.
 13. Користуючись рисунком, де показано положення, швидкість та прискорення тіла в момент часу t = 0, визначити координату тіла через 2 с.
13. Користуючись рисунком, де показано положення, швидкість та прискорення тіла в момент часу t = 0, визначити координату тіла через 2 с.
А. 21 м. Б. 22 м. В. 23 м. Г. 24 м.
14. Два нерухомі автомобілі, відстань між якими 250 м, починають одночасно рухатися назустріч один одному з прискореннями 2 м/с2 та 3 м/с2. Через скільки часу вони зустрінуться?
А. 10 с. Б. 50 с. В. 7 с. Г. 100 с.
1


про публікацію авторської розробки
Додати розробку