Методичні рекомендації "Міжпредметні зв’язки та наступність на уроках математики"

Про матеріал

У посібнику описуеться використання міжпредметних зв’язків, яке спрямоване на формування у школярів системи знань, умінь і навичок, робота з якими розвиває вміння осмислювати зміст понять та застосовувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння, висновки, розширює кругозір учнів,

Перегляд файлу

Міжпредметні зв’язки та наступність на уроках математики

Зміст

1.Вступ

2.Особливості формування ключових компетентностей учнів при навчанні математики

3.Міжпредметні зв’язки в аспекті досліджень великих педагогів.

4.Шляхи реалізації інтеграції і координації навчання математики з іншими предметами шкільного компоненту.

5. Функції та використання міжпредметних зв’язків при викладанні математики.

6. Практична спрямованість навчання математики.

7.Математичні моделі як засіб інтеграції знань.

8.Наступнісність та внутрішньопредметні зв’язки.

9. Мотивації навчання та міжпредметні зв’язки

10. Висновок.

11.Додатки.

12.Список використаних джерел.

1.Вступ.

«Усі знання виростають з одного коріння — з

навколишньої дійсності, а тому

й повинні вивчатися у зв'язках».

Я.А.Коменський

Реформа шкільної освіти в Україні планує перехід від школи знань до школи компетентностей, нова українська школа буде орієнтуватися на навички та вміння. Учнів не будуть перевантажувати знаннями, а вчитимуть потрібним в житті навичкам і вмінню використовувати інформацію на практиці.

Якісне навчання забезпечить засвоєння знань та формування умінь, що для випускника школи стануть підґрунтям у його подальшому житті і майбутній трудовій діяльності. Навчальна діяльність повинна буде не просто дати людині суму знань, умінь і навичок, а сформувати її компетенції, визначити шлях до самовдосконалення. Формування компетентностей учнів зумовлене не тільки реалізацією відповідного оновленого змісту освіти, але й впровадженням інноваційних методів та технологій навчання.

У світлі сучасних завдань реформи школи проблема міжпредметних зв’язків набуває важливого значення.

Актуальність даної проблеми зумовлена розвитком науки, техніки, суспільства. Найвагоміші відкриття відбуваються на стику наук. Спеціаліст будь-якої професії цінується, якщо він володіє високим рівнем загальноосвітніх знань, творчо мислить та здатний до постійного оновлення знань.

Міжпредметні зв’язки є важливим принципом навчання в сучасній школі, що забезпечує взаємозв’язок наук природничо-математичного і суспільно-гуманітарного циклів.

Широке і глибоке проникнення технологій в усі сфери людської діяльності вимагає від молодого покоління, як мінімум, мати базові поняття і знання технологій, які є частиною соціальної культури сучасного суспільства. Міжпредметні зв'язки технологічної і природничо-математичної освіти в цьому смислі мають домінуюче значення.

Проблема не стільки в оволодінні знаннями, скільки в умінні застосовувати їх на практиці в будь-якій життєвій ситуації та у професійній сфері.

Однією з умов вдосконалення природничо-математичної та технічної освіти є зведення до єдиної системи змісту навчальних предметів. Для цього використовують міжпредметні зв’язки з фізики, хімії, математики, біології, географії й інформатики. Ці зв’язки є багатогранними і постійними.

Реалізація міжпредметних зв’язків сприяє розкриттю творчих здібностей кожного вчителя, урізноманітненню методів та організаційних форм навчання для посилення інтересу учнів до знань, активізації мислення, оволодіння системою наукових знань і підвищення результативності всієї навчально-виховної роботи.

2. Особливості формування ключових компетентностей учнів при навчанні математики.

Зміст і методика викладання математики має специфічні особливості щодо формування ключових компетентностей учнів: соціальної, полікультурної, комунікативної, інформаційної, компетенції самоосвіти і саморозвитку, продуктивної творчої діяльності.

На сучасному етапі розвитку суспільства все більше спеціальностей потребують високого рівня освіти, застосувань математичних знань (фізика, хімія, інформатика, бізнес, фінанси тощо), а відтак розширюється коло учнів, для яких математика стає професійно значущим предметом.

Крім того, в повсякденній практичній діяльності,кожна людина має справу з розрахунками, плануванням, моделюванням, прийомами геометричних побудов та вимірювань, складанням та читанням таблиць, схем, діаграм, графіків, виконанням алгоритмів, аналізом масивів даних.

Тому, вивчаючи кожну тему з математики, слід пов’язувати її зміст з практичними задачами з життя чи інших навчальних дисциплін, доводити на конкретних прикладах її практичну значимість та коло застосувань.

«Математика – знаряддя для міркування, бо все, що є на небі, в душі і на землі можна виразити в точному числі. І зовсім нестерпно, коли математик викладає математику без її застосування…» (Р.Фейман)

3.Міжпредметні зв’язки в аспекті досліджень великих педагогів.

Гуманізація освіти спрямована на переорієнтацію самої освіти з предметно-змістовного принципу засвоєння основ наук на вивчення цілісної картини світу та формування системного мислення.

«Наука – це єдине ціле, а поділ її на окремі галузі зумовлений лише обмеженістю людського пізнання, а не природною необхідністю» - так писав фізик Макс Планк.

Процес розвитку природничих наук закономірно призвів до диференціації знань. Це забезпечувало більш ґрунтовний аналіз сфер пізнавальної діяльності. Проте, таке розгалуження спричинило виникнення «кордонів» між галузями знань, навіть близьких між собою.

Я.А.Коменський зазначав, що необхідно «завжди і всюди брати разом те, що пов’язано одне з одним». Необхідність такого підходу до організації навчально – виховного процесу він пояснював тим, що «всі знання виростають з одного коріння – навколишньої дійсності, мають між собою зв’язки, а тому повинні вивчатися у зв’язках».

Великий педагог К.Д. Ушинський вважав, що одним з шляхів досягнення високої якості знань є злиття дисциплін, що вивчаються. Це злиття передбачає порядок і єдність, координацію між елементами знань. Доки різні предмети навчального курсу будуть викладатися, ніби зовсім не знаючи про існування один одного, учіння не буде суттєво впливати на розвиток дітей; доти учіння буде не захоплюючим органічним процесом психічного розвитку, а нестерпно нудною працею для учня.

Суттєвий вплив на подолання предметної автономії, на запровадження у навчально-виховний процес міжпредметних зв’язків мали праці І.П.Павлова, В.О.Сухомлинського, Л.С.Виготського, П.Я.Гольтперіна, І.О.Сікорського.

У 90 – х роках минулого століття інтеграція набула функції механізму гуманізації процесу навчання та була покликана сприяти формуванню у школярів цілісного погляду на світ, подоланню «ефекту клаптикової ковдри» у набутих учнями знаннях.

4.Шляхи реалізації інтеграції і координації навчання математики з іншими предметами шкільного компоненту.

Міжпредметні зв'язки мають вирішальне значення під час розв'язування проблеми інтеграції і координації навчання.

Інтеграція - це процес і результат створення нерозривно пов'язаного, єдиного, суцільного. Нині ця проблема актуальна для школи у зв'язку зі створенням інтегрованих курсів (математика з інформатикою, природознавство, суспільствознавство).

Координація - це погодження навчальних програм зі споріднених предметів з погляду єдиного підходу до трактування понять, ідей, методів, процесів, явищ і в часі їх вивчення міжпредметні зв'язки реалізуються на основі поєднання інтеграції і координації знань, які взаємно доповнюються і сприяють формування в учнів єдиної картини світу, наукового світогляду.

Міжпредметні зв'язки спрямовані на озброєння учнів системою знань зі спрощених предметів: математика – фізика – хімія – біологія - фізична географія - мистецтво - трудове навчання. Реалізація міжпредметних зв'язків має здійснюватись передусім шляхом використання математичних ідей і методів, математичного апарату в інших предметах, вивчення в курсі математики навчального матеріалу, який має важливе значення в спрощених дисциплінах. Важливо також приділяти достатню уваги тому, як математичні задачі виникають на основі задач з інших предметів і як метод розв'язування цих математичних задач використовується у ході розв'язування нематематичних задач. . В наступній таблиці показано деяка наочна ілюстрація міжпредметних зв'язків математики з іншими науками.

предмет	головні питання програми	математична складова
фізика	рівномірний рух, рівнозмінний рух	арифметична прогресія, лінійна і квадратична функція
	шлях при рівноприскореному русі, вільне падіння	квадратні рівняння, графік квадратичної функції
	закон додавання швидкостей	Рух за течією і проти течії, нерівності, алгебраїчні рівняння.
	оптика	перетворення подібності
хімія	задачі на розчини та сплави	відсоткові розрахунки, пропорції
	задачі на змішування розчинів	відсоткові розрахунки, алгебраїчні рівняння, системи лінійних рівнянь з двома змінними
географія	приріст населення	прогресії
географія	побудова плану території	масштаб
біологія	розмноження живих організмів	геометрична прогресія, послідовність чисел Фібоначчі
економіка	продуктивність праці	системи рівнянь, пряма і обернена пропорційність, функціональні залежності
	собівартість	нерівності, геометрична прогресія
	заощадження	відсоткові розрахунки
інформатика	робота з Microsoft Word	діаграми
	робота з Microsoft Excel	діаграми, розв'язування математичних задач, таблиці
	робота з Microsoft PowerPoint	діаграми
	робота з мовами програмування	розв'язування задач і нерівностей
	GeoGebra	графіки функції, геометричних фігур, геометричні перетворення, побудова перерізів

Математиці властива універсальність. Однак, математика не може при цьому замінити методи і поняття тих конкретних наук, де її застосовують, вона має прикладний, підпорядкований характер, служить інструментом у вивченні інших наук.

З цієї точки зору є дуже важливим узгодження у часі і за темпами вивчення програми з математики з програмами інших предметів шкільного компоненту, де використовується математичний апарат.

Надзвичайно цікавим і перспективним є такий спосіб демонстрації зв’язку математики з іншими науками, як проведення нестандартних уроків – інтегрованих або бінарних. Вони формують науковий світогляд, сприяють встановленню логічних зв’язків між предметами, попереджають формалізм у знаннях.(Додаток-презентація « Міжпредметні зв' язки математики і хімії»; додаток 7)

Інтегрувати можна уроки математики з уроками трудового навчання («Формули», «Побудова креслень одягу», «Одиниці маси. Робота з харчовими продуктами. Приготування страв»), географії («Масштаб. Побудова плану шкільної території»), природознавства («Симетрія. Симетрія в природі»), фізики («Швидкість. Одиниці вимірювання швидкості»), історії («Подорож у минуле геометрії», «Сім чудес світу»), біології («Математика на службі генетики»), тощо. Інтегровані уроки мають яскраво виражену прикладну спрямованість і тому викликають незаперечний пізнавальний інтерес учнів.

Міжпредметні зв’язки – це не стільки «мости» між навчальними предметами, але й засіб побудови цілісної системи навчання на основі спільності змісту знань і методів наукового пізнання.

«Немає жодної галузі математики, хоч би якою абстрактною вона не була, що коли-небудь не буде застосованою до явищ дійсного світу», - писав М.І.Лобачевський

5. Функції та використання міжпредметних зв’язків при викладанні математики.

Міжпредметні зв’язки виконують у навчанні математики ряд функцій.

Освітня функція міжпредметних зв’язків полягає в тому, що за її допомогою вчитель математики формує такі якості знань учнів, як системність, глибина, усвідомленість, гнучкість. У цьому випадку міжпредметні зв'язки виступають як засіб розвитку математичних понять, сприяють засвоєнню зв'язків між ними та загальними поняттями.

Розвиваюча функція міжпредметних зв’язків визначається їх роллю в розвитку системного і творчого мислення учнів, у формуванні їх пізнавальної активності, самостійності та інтересу до пізнання математики. Міжпредметні зв'язки допомагають подолати предметну інертність мислення і розширюють кругозір учнів.

Виховна функція міжпредметних зв’язків виражена в їх сприянні всім напрямах виховання школярів у навчанні математики. Учитель математики реалізує комплексний підхід до виховання спираючись на зв’язки з іншими предметами.

Конструктивна функція міжпредметних зв’язків полягає в тому, що з її допомогою вчитель удосконалює зміст навчального матеріалу, методи і форми організації навчання. Реалізація міжпредметних зв’язків вимагає спільного планування вчителями предметів природничого циклу комплексних форм навчальної та позакласної роботи, які передбачають знання ними підручників і програм суміжних предметів.

У ході розв'язування задач, учні виконують складні пізнавальні і розрахункові дії, які впливають на:

Усвідомлення сутності міжпредметних завдань, розуміння необхідності застосування знань із інших предметів;
Відбір та актуалізацію необхідних знань із інших предметів;
Перенесення їх у нову ситуацію, зіставлення знань із суміжних предметів;
Синтез знань, встановлення сумісності понять, одиниць виміру, розрахункових дій, їх виконання;
Одержання результату, узагальнення у висновках, закріплення понять.

Систематичне використання міжпредметних пізнавальних задач у формі проблемних питань, кількісних і практичних завдань забезпечує інтеграцію знань учнів із різних предметів. У цьому полягає найважливіша розвивальна функція навчання математики.

Математика єдиний предмет, який навчає учнів систематизації мислення, точності, аргументації, яскравості визначення, вчить стисло, але точно висловлювати свою думку, достовірно передавати опис того чи іншого предмета. На уроках математики ми застосовуємо такий досвід, коли записуємо умови задачі математичною мовою. Саме в математичній мові втілюється одна із основних ознак краси в науці: зведення складності до простоти.

Математика - це не тільки самостійна наука про «математичні структури», а й мова інших наук, мова єдина, універсальна, точна, проста і красива.

Використання міжпредметних зв’язків - одна з найбільш складних методичних завдань вчителя математики. Вона вимагає знань змісту програм і підручників з інших предметів. Реалізація міжпредметних зв’язків у практиці навчання передбачає співробітництво вчителя з вчителями хімії, фізики, біології, історії, літератури, музики, мистецтва, відвідування відкритих уроків, спільного планування уроків і виховних заходів.

Учитель математики з урахуванням загальношкільного плану навчально-методичної роботи розробляє індивідуальний план реалізації міжпредметних зв’язків у курсах математики 5 - 11 класів. Методика творчої роботи вчителя включає ряд етапів:

Вивчення розділу «міжпредметні зв'язки» у кожному математичному курсі і опорних тем із програм і підручників інших предметів, читання додаткової наукової, науково-популярної та методичної літератури;
Поурочне планування міжпредметних зв’язків із використанням тематичних планів;
Розробка засобів і методичних прийомів реалізації міжпредметних зв’язків на конкретних уроках;
Розробка методики підготовки і проведення комплексних форм організації навчання;
Розробка прийомів контролю і оцінки результатів здійснення міжпредметних зв’язків у навчанні.

Міжпредметні зв’язки впливають на склад і структуру навчальних предметів. Кожен навчальний предмет є джерелом тих чи інших видів міжпредметних зв’язків. Тому можливо виділити ті зв’язки, які, враховуються в змісті математики, і, навпаки, - йдуть від математики в інші навчальні предмети.

Формування загальної системи знань учнів про реальний світ, що відображають взаємозв’язки різних форм руху матерії – одна з основних освітніх функцій міжпредметних зв’язків. Формування цілісного наукового світогляду вимагає обов’язкового обліку міжпредметних зв’язків. Комплексний підхід у вихованні посилив виховні функції міжпредметних зв’язків курсу математики. У цих умовах зміцнюються зв’язки математики як із предметами природничо-наукового, так і гуманітарного циклу; поліпшуються навички перенесення знань, їх застосування і різностороннє осмислення.

Міжпредметні зв’язки – це сучасний принцип навчання, який впливає на відбір і структуру навчального матеріалу цілого ряду предметів, посилюючи системність знань учнів, активізує методи навчання, орієнтує на застосування комплексних форм організації навчання, забезпечуючи єдність навчально-виховного процесу.

6.Практична спрямованість навчання математики.

Впродовж вивчення шкільного курсу математики неможливо обійтися без задач прикладного змісту. Прикладними задачами у математиці називають ті, умови яких містять нематематичні поняття.(Додатки 5,6)

Прикладні задачі на уроці виконують кілька функцій: показують зв'язок математики з життям, підвищують економічну грамотність учнів, розвивають інтерес до математики. Задачі практичного змісту переконують учнів у необхідності вивчення теоретичного матеріалу і показують, що математичні абстракції виникають із задач поставлених реальним життям. Міжпредметні зв'язки є відображенням тих взаємозв'язків, які діють у природі.

Під час добору задач доцільно дотримуватися певних вимог. Задача має демонструвати практичне застосування математичних ідей і методів та ілюструвати матеріал, що викладається на певному уроці, містити відповідні або інтуїтивно зрозумілі учням поняття і терміни, а також реальні числові дані, що не ведуть до громіздких обчислень. За таких умов використання прикладної задачі, складеної на матеріалах суміжних предметів, дає педагогічний ефект.

Практика свідчить про доцільність проведення уроків математики з інтегрованим змістом. Зокрема, використання задач з екологічним сюжетом на основі краєзнавчого матеріалу, довкілля. За умови розв’язування таких задач знання учнів поповнюються цікавими відомостями про навколишній світ, розвивається і вдосконалюється математична мова, увага, самостійне творче мислення, виховуються елементи основ екологічної культури.

Наведемо приклади цікавих числових відомостей екологічного спрямування, а також задач, що їх можна використовувати під час вивчення деяких тем з математики:

Обчислити, скільки кубічних метрів повітря очистить від автомобільних викидних газів 25 каштанів, посаджених вздовж дороги, якщо одне дерево очищує зону довжиною 100м, шириною 20 м, висотою 10 м без шкоди для себе.
Загальні запаси води на планеті 1800 млн. км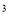. На світовий океан припадає 98%. Прісна вода становить 2%, з них тільки 1% перебуває в рідкому стані.
1м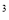неочищених стічних вод забруднює 50 м 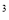чистої води.
Щоб зібрати 1кг меду, бджола робить 50 тисяч вильотів і відвідує 10 млн. квітів.
Із 264г листя сухої кропиви можна виготовити 8 порцій ліків для зупинки кровотечі. Скільком хворим може допомогти хлопчик, що заготовив 1485г листя?
Мурашина сім'я протягом дня знищує близько 1кг комах, завдяки чому захищає ліс площею 2500 м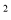, тому за руйнування мурашника накладається штраф 230 грн.
Територія України поділяється на такі ботаніко-географічні зони Полісся, Лісостеп, Степ, Карпати, Крим, у яких площа лісів становить відповідно: 40%, 25%, 10%, 22%, 3%. Побудувати діаграму розміщення лісів у порядку зростання.
Скільки людей забезпечує киснем кожна ботаніко-географічна зона, якщо лісовий фонд становить 96862 тисяч га?

Про те, що математика як обчислювальний інструмент має допомагати вивченню фізики – зрозуміло всім. Повну картину фізичного явища можна отримати лише тоді, коли ці явища вдається кількісно виміряти і описати мовою математичних співвідношень.

Вивчаючи тему «Стандартний вигляд числа» доцільно розглянути застосування запису чисел у стандартному вигляді при розв’язуванні задач з фізичним змістом. Наприклад, для виготовлення електроліту потрібна дистильована вода, яка добувається шляхом випаровування природної води. Яку кількість теплоти треба витратити для випаровування 20т води, взятої при температурі кипіння? (Q=mr, де m=2·10кг, r=2,257· 10 Дж/кг).

При вивченні теми «Прогресія» доцільно згадати досліди подружжя Кюрі, що привели до відкриття радіоактивності і закону розпаду атому; закон вільного падіння і рівноприскореного руху.

Вивчаючи пряму і обернену пропорційності, можна розв’язати задачі про сполучені посудини, або про важелі: «Довжина меншого плеча важеля 5см, більшого 30см. На менше плече діє сила 12Н. Яку силу треба прикласти до більшого плеча, щоб зрівняти важіль?»

Вивчаючи тему «Об’єм» можна навести безліч цікавих фактів, що демонструють зв'язок математики з іншими предметами шкільного компоненту (з історією – єгипетські піраміди; з образотворчим мистецтвом – особливості передавання об’ємності предметів за допомогою графіки і живопису, приклади зорових ілюзій неіснуючих предметів; з англійською мовою – англійські міри об’єму; з фізичною культурою – форма багатьох спортивних знарядь: ядро, м’яч, граната, спис, обруч тощо; з екологією – об’єм втраченої води з несправного крану; з біологією – форма вірусів, бджолині соти ; з географією – об’єм щорічних опадів на Землі, об’єм льодовиків в Антарктиді; з космічними дослідженнями – об’єм штучного супутника Землі, тощо.

Математика може сприяти вихованню національної самосвідомості, що є актуальним в наш час, коли Україна перебуває в процесі національного відродження. Для цього можна розв’язувати задачі на історичну тематику (Додаток 1)

Патріотизм – це почуття любові до Батьківщини, гордості за досягнення її народу. Українська нація багата на таланти і переконати учнів в цьому можна, розв’язуючи задачі:

Найменша книжка в світі – мікромініатюрний «Кобзар», створена українським майстром М.Сядристим. Довжина сторінки – 0,84 мм, ширина на 0,13 мм менша. Знайти площу «Кобзаря» та найменшої японської книжки, що в 19 разів більша від «Кобзаря».
Розмах крил «Боїнга – 747» - 64,92м, а українського літака «Мрія» - на 23,48м більша.

Неможливо виховати справжню людину, якщо вона не знає свого краю, його історії і сьогодення. Тому доцільно використовувати «місцеві» матеріали для складання задач, (Додаток 2) наприклад, завдання з алгебри, 7 клас.

№1

Тема: «Степінь з натуральним показником»

Вирази

(-1)²⁸

(-3)²

2³

(-3)³

(-8)²

(-3)⁴

(-2)³

(-1)¹³

(-5)³

1¹⁷

9²

2¹

Відповіді

Букви

17 вересня 1864 року у місті Вінниця народився видатний класик української літератури. Тут він написав значну частину своїх творів, вчителюючи і вивчаючи життя, побут та звичаї селян Поділля. Дізнатися прізвище відомого письменника допоможе вам запропонована шифрограма.

Ключ до шифру:

Букви	и	к	о	н	б	ц	с	ь	й	ю
Відповіді	81	1	9	-8	64	8	-1	-125	2	-27

Вирази

(-1)²⁸

(-3)²

2³

(-3)³

(-8)²

(-3)⁴

(-2)³

(-1)¹³

(-5)³

1¹⁷

9²

2¹

Відповіді

-27

-8

-1

-125

Букви

Розв`язання:

Відповідь: М. Коцюбинський.

№2

Тема: «Лінійні рівняння з однією змінною»

Щоб дізнатися, в якому році було засноване місто Вінниця, розв`яжіть рівняння:

(х - 89) : 98 = 13

Розв`язання:

х – 89 = 13 · 98

х – 89 = 1274

х = 1274 + 89

х = 1363

Відповідь: у 1363 році.

Якщо зв'язок математики і фізики є очевидним, то гуманітарії таких зв’язків не бачать і часто заперечують. Проте знайти ці зв’язки можливо. Завдяки використанню художньої літератури на уроках математики можна розв’язувати задачі виховання, що дозволяє гармонізувати обстановку в класі, де є і логіки, і лірики.(Додатки 3,4)

Звернення до класиків літератури на уроках математики подобається учням, сприяє підвищенню інтересу до математики, зайвий раз демонструє взаємозв’язки математичного та гуманітарного напрямів. Цікавими є віршовані задачі, що розв’язуються способом складання рівнянь (історична - «Прах Діофанта» та задача про учнів Піфагора; історично-літературна задача про гусей, яку запропонував Суворов маленькому Пушкіну, коли гостював у будинку Ганнібала, тощо)(Додаток 8).

Пов’язати математику з хімією дають змогу задачі на суміші і сплави.

7.Математичні моделі як засіб інтеграції знань.

Реалізувати міжпредметні зв'язки під час вивчення математики означає насамперед створити запас математичних моделей, які описують явища і процеси, що вивчаються в різних предметах. Такими моделями є основні поняття математики: величина, число, функція, фігура, рівняння, похідна, інтеграл, диференціальне рівняння, ймовірність тощо. Наприклад, похідна - це математична модель різних фізичних, хімічних, біологічних понять: швидкості прямолінійного нерівномірного руху, швидкості реакції в хімії, електрорушійної сили, індукції як швидкості зміни магнітного потоку, швидкості розмноження бактерій та ін. До математичних моделей прикладних задач можна віднести такі важливі математичні задачі: знайти розв'язок алгебраїчного рівняння, знайти найбільше і найменше значення функції, знайти розв'язок диференціального рівняння, що задовольняє деякій початковій умові, знайти закон розподілу деяких випадкових величин.

Математичні моделі дають можливість ознайомити учнів із математичними пізнаннями дійсності. У процесі розв’язування текстових задач, починаючи з молодших класів, учні неявно ознайомлюються з найпростішими видами математичних моделей. Побудова останніх передбачає перехід від реальної ситуації до рівняння.

Вивчення функцій дає змогу не лише розкрити залежність між величинами, що характеризують різні процеси діяльності, але й розкрити універсальні моделі.

Лінійна функція є аналітичним записом:

залежності між швидкістю і часом для рівномірно прискореного руху ;
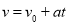залежність довжини стрижня від його температури ;
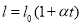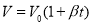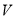закон Гей-Люссака , де - об’єм газу із сталим тиском, 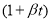- біном об’ємного розширення ;
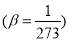закону Шарля 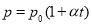, де 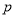- тиск газу зі сталим об’ємом;
калорійність молока 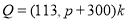, де 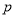- жирність молока у %, 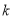- добовий надій молока в кг, 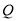- кількість ккал у добовому надої;
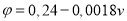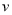коефіцієнт тертя гальмівної колоди , де - швидкість руху потягу;
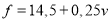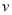опору дороги з асфальтовим покриттям , де - швидкість руху автомобіля.

Прямо пропорційна залежність моделює:

залежність між масою та об’ємом за сталої густини ;
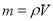залежність між вагою тіла і масою ;
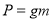залежність між шляхом і часом у рівномірному русі ;
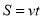залежність між вартістю і кількістю купленого товару ;
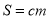залежність між довжиною кола та його діаметром ;
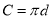залежність сили пружності від деформації ;
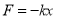залежність заряду конденсатора від напруги в ньому ;
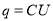залежність напруги на кінцях провідника від сили струму ;
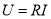залежність потоку магнітної індукції, який пронизує контур, від сили струму в ньому ;

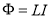Квадратична функція є аналітичним записом:

площа квадрата зі стороною а ;
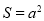площа круга з радіусом , ;
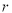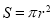шляху тіла, що вільно падає ;
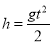періоду коливання математичного маятника ;
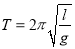швидкості тіла, що падає з висоти h (без урахування опору повітря) ;
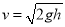опору вантажівки (на клінкерному шосе), який залежить від його швидкості ;
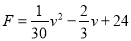залежність енергії рухомого тіла зі сталою масою від його швидкості ;
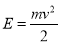залежність кількості тепла Q, що виділяється в провіднику за певний проміжок часу, від сили струму, опору провідника і часу проходження струму .

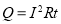Парабола.

Графік квадратичної функції зображує: параболічну арку або звід мосту; трос висячого мосту; параболічний виліт крана; параболоїд рідини, що перебуває в обертальному русі; траєкторію тіла, кинутого під кутом до горизонту; траєкторію потоку - струменя рідини.
Парабола в оптиці і радіотехніці: телескоп-рефлектор; прожектор або фара автомобіля; рефлектор сонячної електростанції; медичний рефлектор; збільшувальне дзеркало; параболічні антени тощо.
У спорті параболічну траєкторію під час свого вільного руху описують футбольний м'яч, центр ваги спортсмена-стрибуна, молот.
рівняння траєкторії ;
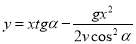дальність польоту ;
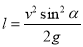максимальна висота .

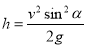Математичною моделлю фактичної взаємодії двох матеріальних тіл формула , що виражає сила взаємодії двох матеріальних точок.

Рівнянням можна виразити такі фізичні залежності:

опір ділянки кола, складеного з паралельного з'єднаних провідників ;
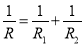ємність батареї конденсаторів, з'єднаних послідовно ;
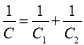формулу лінзи .

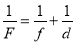Степенева функція з натуральним показником виражає:

залежність між силою опору середовища і швидкості руху ;
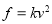закон Джоуля-Ленца ;
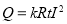закон Стефана-Больцмана 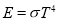, де Е- повне вимірювання енергії з одиниці площі абсолютного чорного тіла, Т- абсолютна температура.

Степенева функція з цілим від'ємним показниками виражає:

залежність опору від діаметра провідника ;
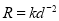залежність сили притягання до Землі ;
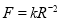закон освітленості точковим джерелом світла ;
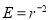закон гідродинаміки Д.Бернуллі .

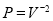Степенева функція з ірраціональним показником виражає:

період коливання математичного маятника ;
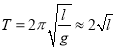час вільного падіння тіла ;
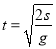діаметр водопровідної труби (у м) 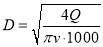, де Q - це витрати води (у л/с), v - швидкість руху води ( у м/с).

Показникова функція описує такі реальні процеси:

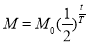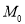закон радіоактивного розпаду , де - початкова кількість атомів, - кількість атомів через од. часу, 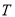- період напіврозпаду;
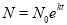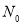закон розмноження бактерій , де - початкова кількість бактерій, 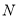- кількість бактерій через проміжок часу 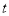, 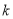- стала зростання, що визначає швидкість розмноження бактерій;
закон зміни тиску залежно від висоти h над рівнем моря (у км) 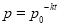, де 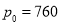мм рт.ст.

Логарифмічна функція моделює такі процеси:

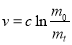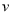закон зміни швидкості ракети (формула Ціолковського) , де - швидкість ракети, 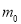- маса ракети разом із паливом до початку руху, 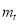- маса ракети в певний момент часу;
закон зміни роботи газу 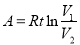, де об'єм газу змінюється від 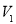до 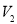, , 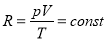Т абсолютна температура;
закон зміни сили відчуття від сили збудження (психофізичний закон Вебера в математичному формулюванні Фехнера) 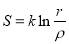, де 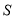- сила відчуття, r – сила відповідного збудження, 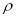- порогове збудження;
закон зміни тиску P залежно від зміни висоти 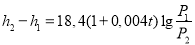, де 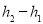- зміна висоти, - температура повітря;
тривалість хімічної реакції 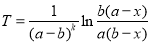, де Т- час необхідний для утворення x молекул внаслідок хімічної реакції, a, b - початкова кількість реагентів, які вступають в реакцію водночас.

Тригонометричні функції описують: коливальні процеси; зовнішні межі викройки для розкроювання тканини (область рукава); бляхи для скручування труб і з'єднання їх «у коліно» тощо.

Побудова математичної моделі фізичного явища є звичайною з часів І. Ньютона, а фізичне моделювання як засіб розв'язування математичних задач використовується рідко, хоча має давню традицію.

Наприклад, використання законів фізики допомогло Архімеда довести теорему про медіани трикутника. Для закріплення цього доведення учням варто запропонувати такі задачі.

Задача 1. На ребрах тетраедра взято точки відповідно так, що . Через ці точки проведено площину. В якому відношенні ця площина ділить ребро ?

(1:2)

Задача 2. У трикутнику сторони відносяться, як 1:3, - бісектриса, на якій взято точку О так, що . Через А та О проведено пряму. В якому відношенні пряма АО ділить сторону ВС?

(1:2)

Моделі відіграють важливе значення і в теорії хімічної будови речовини О. М. Бутлерова.

Їх розгляд дає можливість зробити такі висновки:

формули будови слід розглядати як певні знакові моделі;
формула будови, як і будь-яка знакова модель відображає хімічну будову молекули;
первісне зображення будови молекули дає уявлення про склад хімічний зв'язок атомів, зокрема про їх просторове розміщення;
у процесі розвитку теорії будови формули поступово відображали просторові розміщення, ставали адекватними моделями молекул.

Основною геометричне характеристикою молекули насичених вуглеводів є кут між зв'язками, тобто між лініями, вздовж яких перекриваються електронні хмари атомів. Розглянемо, наприклад, молекулу метану : чотири атоми водню розміщуються у вершинах правильного тетраедра, а атом вуглецю - у центрі. Найміцніші хімічні зв'язки утворюються в тому випадку, коли лінії перекриття електронних хмар проходять вздовж ліній, які з'єднують ці атомом. Величина кута між ними – 109,28˚. Математичну модель можна отримати, розглянувши таку стереометричну задачу: визначити величину кута, утвореного відрізками, які сполучають центр правильного тетраедра з його вершинами.

Учням, ознайомленим з комбінаторикою, доцільно запропонувати такі задачі:

Скільки різних пентапептидів можна скласти з восьмим амінокислотних залишків? (.)
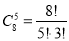Скільки різних пентапептидів можна скласти з восьми амінокислотних залишків, щоб вони відрізнялися не лише складова, але й порядком? ( .)
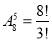Скільки ізомерів октапептидів можна скласти з восьми різних амінокислотних залишків? (.)

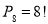Розглянуті вище приклади дають уявлення про можливість ознайомлення учнів з методом математичного моделювання, коли формуються такі розумові здібності, як узагальнення, аналогії тощо. Їхній мозок поступово орієнтується на виділення з навколишнього світу подразників типу просторових і числових відношень та символів, на оптимальну роботу саме з такими подразниками. Нарешті моделювання переноситься на інші методи теоретичного пізнання і підпорядковує їх собі.

Цей метод розкриває:

перспективи змістової класифікації задач із різних предметів за типологією моделей та моделювання, що передбачаються умовою;
перспективу глибшого усвідомлення структури, етапів дослідження і розв'язування задач з математики в середній школі.

8.Наступнісність та внутрішньопредметні зв’язки.

З реалізацією внутрішньопредметних зв'язків тісно пов'язана проблема наступності навчанні. У «Педагогічній енциклопедії» зазначається, що наступність у навчанні полягає в установлені необхідного зв'язку і правильного співвідношення між частинами навчального предмета на різних ступенях його вивчення. У педагогіці під знаннями розуміють не будь-яку інформацію, а лише ту, яка має якість системності, тобто якість знань, яка характеризує наявність у свідомості учня структурних зв'язків або зв'язків будови знання всередині наукової теорії. Маються на Дуже цікавим є пошук і відображення взаємозбагачуючих зв’язків між різними науками увазі зв'язки між поняттями, твердженнями, способами розв'язування задач. Тому потрібна цілеспрямована систематична робота вчителя для встановлення зв'язків і відношень між різними елементами знань. Враховуючи концентричний характер побудови програми з математики, слід забезпечити єдиний підхід у трактуванні понять, способах діяльності учнів і обов'язкову опору на вже засвоєних учнями знання. Наприклад, вивчаючи геометричні величини в систематичному курсі геометрії, важливо актуалізувати уявлення, знання та навички, якій учні здобули в 1-6 класах. Справді, на рівні практичних дій учнів переконалися у властивостях довжини відрізка, величини кута, які в геометрії формулюються у вигляді аксіом. Ще один приклад. Вивчення алгебраїчних дробів у восьмому класі спирається на аналогічні властивості дій, що стосуються звичайних дробів, які вивчали у п'ятому і шостому класах.

Реалізація внутрішньо предметних зв'язків полягає в тому що, кожний навчальний рік починається з повторенням і систематизації головного, вивченого учнями в попередні роки по основних змістових лініях. Вивчення кожної нової теми починається з повторення того, що учні вже знають і що пов'язано з новим навчальним матеріалом. Це дає змогу всім учням усвідомити зв'язки між засвоєним і новим.

Реалізації внутрішньо предметних зв'язків сприяє використання аналогії у процесі навчання математики. Наприклад, в стереометрії означення багатьох понять формулюються аналогічно спорідненим поняття планіметрії. Крім того, розв'язування більшості стереометричних задач зводиться до планіметричних. Тому важливо, з одного боку, забезпечити свідоме і міцне засвоєння головного у планіметрії, а з іншого - систематично повторювати цей матеріал і вміло актуалізувати його з метою вивчення відповідного матеріалу зі стереометрії.

9. Мотивації навчання та міжпредметні зв’язки

Мотивація, або прагнення дитини до навчання, є одним із найважливіших чинників, що забезпечують успішне сприйняття і засвоєння учнями програмового матеріалу.

Одноманітна за структурою навчальна діяльність призводить до втрати інтересу, знижує ефективність сприйняття учнем матеріалу, що вивчається.

Формувати мотивацію означає створити для учня такі умови та ситуації, які змогли би активізувати розумову діяльність, де бажані мотиви і цілі розвивалися би з урахуванням життєвого досвіду та внутрішніх прагнень самого учня.

При підготовці до уроку ретельно продумана мотивація на рівні внутріпредметного та міжпредметних зв'язків визначає значимість теми уроку для розвитку науки, повсякденного життя, розв'язання економічних проблем, пізнання світу, фактів та явищ, підвищує усвідомлення матеріалу, що вивчається.

Логіка процесу навчання полягає в русі від представлення матеріалу через пояснення до розуміння, узагальнення, використання набутих знань на практиці. Прагнення людей до знань актуальних і прикладних значно вищі, ніж до абстрактних і непрактичних. Тому поєднання теоретичних знань з можливістю їх застосування до розв’язування задач в різних галузях науки та людської діяльності підвищує значущість предмета, формує в учнів дійсні уявлення про математику та її широке прикладне спрямування.

10. Висновок.

Використання міжпредметних зв’язків спрямоване на формування у школярів системи знань, умінь і навичок, робота з якими розвиває вміння осмислювати зміст понять та застосовувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння, висновки, розширює кругозір учнів. Такі задачі зумовлюють потребу у вивченні теоретичного матеріалу, свідчать, що математичні абстракції виникають із реального життя. Вони зацікавлюють розв’язуванням, вивченням окремих тем, а з часом учні відчують потребу у вивченні математики.

Практичні задачі допомагають висвітлювати міжпредметні зв’язки, які, у свою чергу, зумовлюють поглиблене і розширене сприйняття учнями фактів, свідоме засвоєння теорії, формування цілісної картини природи та світу. Міжпредметні зв’язки є відображенням тих взаємозв’язків, які діють у природі, а також є засобом, що забезпечує взаємну узгодженість учбових програм і підручників з різних предметів, слугує підвищенню наукового рівня викладання основ наук, формування діалектичного світогляду учнів, розвитку їх творчих здібностей, а також чинником взаємодії наук у процесі формування світогляду школярів і зростання їх пізнавальних інтересів.

Використання міжпредметних зв’язків є одним з напрямків сучасної освіти і забезпечує розвиток нового, творчого покоління громадян нашої держави.

11. Додатки

Додаток 1

З досвіду роботи з патріотичного виховання

Конспект уроку з математики

5 клас

Урок-мандрівка до Запорозької Січі

Тема уроку: Додавання і віднімання натуральних чисел

Мета уроку:

навчальна: узагальнити й систематизувати відомості про натуральні числа, зокрема про додавання й віднімання натуральних чисел; закріпити вміння і навички застосування цих дій до розв’язання задач.
розвиваюча: розвивати логічне мислення та уяву;
виховна: виховувати культуру математичного мовлення; уміння працювати в групі; доброзичливість; повагу до минулого українського народу.

Обладнання: плакати, кросворди, листи з завданням, презентація.

Тип уроку: узагальнення й систематизація знань.

Форма уроку: урок-мандрівка.

Хід уроку

І. Мотивація навчальної діяльності учнів.

ІІ. Організація навчальної діяльності учнів.

На уроці ми будемо узагальнювати й систематизувати знання, вміння та навички, які стосуються додавання й віднімання натуральних чисел. Для цього ми здійснимо мандрівку. Помандруємо ми з вами в часи козацькі до Запорозької Січі десь так на 500 років назад.

1 етап мандрівки. Шлях до Січі.

Задача 1.

У 1556 році на острові Мала Хортиця було засновано фортецю, що поклала початок Запорозькій Січі. Скільки років минуло з того часу?

Що ж являв собою острів Хортиця? Про його розміри ви дізнаєтесь, якщо розв’яжете задачу.

Задача 2.

Хортиця – найбільший дніпровський острів. Він заввишки сягає 2 км. 500м., а довжину має на 9 км. 500м. більше. Яка довжина острова Хортиця?

Щоб потрапити на цей острів, козакам потрібно було подолати Дніпровські пороги, а нам з вами треба знайти закономірність і замість знака питання записати число.

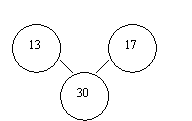
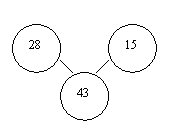
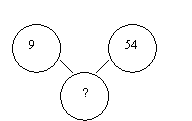
Впоравшись з завданням, ми потрапляємо на острів.

2 етап мандрівки. Козацька наука.

Тут козаки створювали для дітей 10-11 років школи, учнів яких називали …

Як називали майбутніх козаків ми дізнаємось, розв’язавши наступне завдання.

Обчисліть найзручнішим способом, використовуючи властивості додавання і віднімання.

А) 11+12+12+17+18+19=30+30+30=90 (д)

Б) (547+204)+496=547+700=1247 (ж)

В) (237+118)-37=237-37+118=200+118=318 (у)

Г) 729-(513+129)=729-129-513=600-513=87 (р)

Д) 928+(524-428)=928-428+524=500+524=1024 (и)

3 етап мандрівки. Бойова задача.

Крім обов’язкових знань з математики, риторики, письма, у школі джури вивчали військову справу, вчилися володіти зброєю та способами виживання. Запорізьке військо славилося своєю високою боєздатністю і військовою майстерністю. Козаки вважалися великими майстрами артилерійської справи.

Задача.

На Січі постійно було 50 гармат. Артилерія – це дуже дорога зброя, тому зайві гармати зберігалися у Військовій Скарбниці (Зміїній печері) в потаємному місці на рівні з коштовностями. Гармата середнього калібру коштувала стільки, скільки коштувало стадо із 442 корів, а один постріл такої гармати коштував, як 9 корів. Підрахуйте, у скільки корів обходились козакам 50 гармат та один постріл з них.

Розв’язання:

442+9=451(корова)
451*50=22550(корів)

Відповідь: 50 гармат і один постріл з них коштували стільки, скільки і 22550 корів.

4 етап мандрівки. Математична зарядка.

Незважаючи на бойову вдачу козаків, вони іноді помилялися в своїх розрахунках.

Самостійна робота. Знайти помилки у рівняннях:

х+160=360

х=360+160

х=520 (200)

(м-124)+316=900

м-124=900-316

м-124=584

м=460 (708)

206-у=139

у=139+206

у=345 (67)

Як знайти невідомий доданок, зменшуване, від’ємник?

Перевірка здійснюється у вигляді математичної зарядки. Учитель називає пункт, а учні у разі правильної відповіді піднімають руки вперед, неправильної – вгору.

5 етап мандрівки. Господарювання.

Крім бойових козаків, були козаки, які займались господарюванням: хліборобством, мисливством, рибальством, садівництвом, торгівлею та ремеслом. Хлопчики-джури вчились та допомагали старшим господарювати. Закладалися сади, де росли груші, яблука і вишні. Завітаймо до одного з таких садів.

Задача.

У саду було 6000 дерев. Груш і яблунь всього 3200, решта дерев – вишні. Скільки посадили яблунь, коли відомо, коли відомо, що груш посадили на 1500 менше, ніж вишень?

Розв’язання:

6000-3200=2800 (вишень)
2800-1500=1300 (груш)
3200-1300=1900 (яблунь)

Відповідь: 1900 яблунь.

6 етап мандрівки. Козацький курінь.

Подивіться уважно на схеми. На них по два слова зашифровані числами, а третє слова не зашифроване. Вам необхідно записати число, що відповідає третьому слову.

І варіант

Діти – 4672

Вік – 563

Квіти - ?

(35672)

ІІ варіант

Вухо – 8671

Жук – 356

Кожух - ?

(51357)

7 етап мандрівки. Час змужніння.

Після закінчення навчання, хлопчики-джури посвячувались в молоді козаки, якщо успішно поверталися разом із старшими товаришами із морського походу.

У морські походи запорожці відправлялися на великих човнах, які називалися «Чайками». Про розміри козацьких човнів та їх швидкість ви дізнаєтесь, розв’язавши задачішД/З.

ІІІ. Рефлексія

IV. Підсумок уроку.

V. Оцінювання учнів.

V. Домашнє завдання.

Задача 1.Чайка мала однакові ширину (у верхній частині) та висоту, що у 5 разів менша за її довжину. Днище чайки довжиною 16м. робили суцільним, зі стовбура верби або липи. Сума розмірів чайки становила 44м. Які розміри мав козацький човен чайка?

Задача 2. Замість «*» поставте потрібні цифри:

*48**

+38*96

*55*4

Додаток 2

5 клас

№1

Видатний хірург, учений і винахідник Пирогов Микола Іванович народився

13 листопада 1810 року, а помер 23 листопада 1881 року. Скільки років, місяців

і днів прожив М.І. Пирогов?

Розв'язання

1881 – 1810 = 71 років прожив М.І. Пирогов

71∙12 = 852 місяців прожив М.І. Пирогов

71∙365 + (23 – 13) = 25915 +10 = 25925 днів прожив М.І. Пирогов не враховуючи високосні роки.

25925 + 18 = 25943 днів прожив М.І. Пирогов

Відповідь: 71р., 852 м., 25943 дня.

№2

Знайдіть відстань між містами побратимами Вінниця (Україна) і Кельце (Польща), якщо її можна подолати за 11 годин рухаючись із середньою швидкістю 63 км/год.

Розв'язання

Оскільки s=v∙t, то

s= 63∙ 11 =693 (км)

Відповідь: 693 км.

В задачі № 2 пригадуємо правило усного множення двоцифрового числа на 11.

63∙ 11 =693, де 9 = 6+3

6 клас

№1

Площі центрального парку ім. Горького і парку Дружби народів відносяться як 4:9. Загальна їх площа 130 га. Знайти площі парків.

Розв’зання.

4+9=13 (га) - всього частин;
130:13= 10(га) – одна частина;
10×4=40 (га) – площа центрального парку ім. Горького ;
10×9= 90 (га) - площа парку Дружби народів .

Відповідь: 40 га, 90 га .

№2

Довжина вулиці Хрещатик м. Київ дорівнює 1,2 км , що становить 75% довжини центральної вулиці Соборної м. Вінниці. Знайти довжину вулиці Соборної.

Розв’зання.

75%=0,75;
1,2:0.75=1,6 (км) - довжина вулиці Соборної.

Відповідь: 1,6 км.

8 клас

№1

Подайте величини у стандартному вигляді:

місто Вінниця займає площу 113,2 км²;
населення Вінниці станом на 1 лютого 2015 року складає 372400 мешканців;
автомобільні шляхи Вінниці становлять 365,5 км;
висота Вінницької телевежі складає 354 м, що вище, за Ейфелеву вежу;
площа Центрального міського парку Вінниці становить 40 га.

№2

Розв'язавши рівняння, ви прочитаєте прізвище видатного вченого, геніального хірурга, засновника-творця воєнно-польової хірургії, педагога і громадського діяча, який впродовж останніх 20 років свого життя (1861 – 1881) жив і працював у Вінниці.

-9х² = 0;
х² + 8х + 12 = 0;
х² - 9 = 0;
9х² + 1 = 0;
х² – 3х + 2 = 0;
х² + 4х + 5 = 0;
3х² – 6х = 0.

Відповіді	-3 ; 3	0 ; 2	1 ; 2	розв'язку немає	0	-6 ; -2
Букви	Р	В	Г	О	П	И

Відповіді:

Задача №1:

1,132∙10² км²;
3,724∙10⁵ мешканців;
3,655∙10² км;
3,54∙10² м
4∙10¹ га

Задача №2

-9х² = 0 0 П
х² + 8х + 12 = 0 -6 ; -2 И
х² - 9 = 0 -3; 3 Р
9х² + 1 = 0 розв'язку немає О
х² – 3х + 2 = 0 1; 2 Г
х² + 4х + 5 = 0 розв'язку немає О
3х² – 6х = 0 0; 2 В

9 клас

№1

Задача:

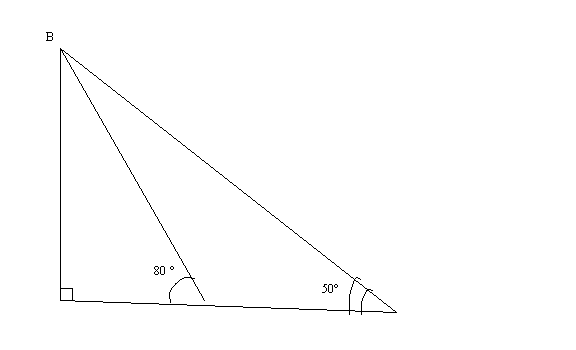
Розв`язання:

1) BCA - зовнішній кут ∆ BCD

BCA = CBA + BDC, отже

CBD = 80 – 50 = 30( º)

2) Із ∆ BCD за теоремою синусів

CD BC

—— = ——

sin B sin D

CD · sin D 18, 5 · sin 50º 18,5 · 0, 7660

BC = ――――― = ——————— = ―――――― = 28, 342 (м)

sin B sin 30º 0, 5

3) ∆ ABC – прямокутний

AB = BC, sin C

AB = 28, 342 · sin 80º = 28, 342 · 0, 9848 = 27, 91

27, 91 ≈ 28

Відповідь: 28 м

11 клас

№ 1

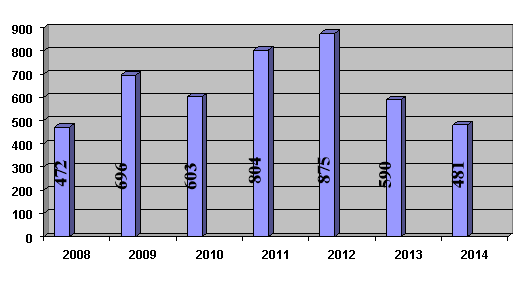
На стовпчиковій діаграмі зображено природний приріст населення м. Вінниця за останні роки.

Приріст населення.

Використовуючи діаграму з’ясувати:

За який рік приріст населення м. Вінниці був:

а) найбільший.

б) найменший.

За який рік приріст населення становив 603 людини?
Вказати чинники, які, на Вашу думку, привели до зменшення приросту за 2014 рік.

Розв’язання:

а) за 2012 рік; б) за 2008 рік;
за 2010 рік;
Серед всіх інших можна сказати: війна в країні; міграція населення( - 172 особи за 2013 рік. – 113 особи за 2014 рік.); економічний спад; зменшення кількості робочих місць; знецінення гривні.

Додаток 3

6 клас

Тема уроку: Дії з десятковими та звичайними дробами.

Мета уроку: закріпити та узагальнити вміння та навички учнів під час виконання дій з дробами, познайомити учнів з відомостями із життя і творчості О. С. Пушкіна. Розвивати логічне мислення, спостережливість, розширювати ерудицію.

Тип уроку: Узагальнення та систематизація вивченого, практичного застосування знань, умінь, навичок.

Обладнання: презентація, портрет О. С. Пушкіна, твори поета, листки із завданнями.

Хід уроку

Організаційний момент.

Кожен учень отримує листок з надрукованими завданнями для індивідуального та колективного розв’язування.

Фронтальна актуалізація знань і способів дій.

Перевірка наявності та правильності виконання домашнього завдання.
Усна лічба.

Обчислити і розмістити у порядку зростання значення виразів:

(У)

(К)

(Н) :

(П)

(Ш)

(І):

	1		6	8	10
П	У	Ш	К	І	Н

Повідомлення теми та мети уроку.

Вчитель: сьогодні на уроці ми не тільки повторимо дії із звичайними та десятковими дробами, а й познайомимося з деякими фактами з життя і творчості видатного російського поета О. С. Пушкіна.

Розв’язування вправ

Виконання кожним рядом завдань, відповіді до яких будуть цифрами, що утворюють дату народження і рік смерті О. С. Пушкіна.

Перший ряд

Розв’яжіть рівняння

А)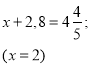

Б)

2) Обчислити значення виразу

А)

Б)

Другий ряд

1) Розв’яжіть рівняння

А)

Б)

2)Обчислити значення

виразу

А)

Б)

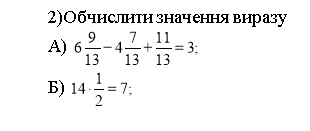Третій ряд

Розв’яжіть рівняння

А)

Б)

Після розв’язування вправ учні одержують 26.05.1799 та 1837, тобто дату народження та рік смерті О. С. Пушкіна.

Колективне розв’язування задачі про тривалість життя О. С. Пушкіна.

Задача. Як відомо, О. С. Пушкін 120 років прожив у Москві, року – в Царському селі, року – в Петербурзі, року відбував заслання на Півдні, року знаходився у селі Михайлівське, року перебував у Петербурзі, Москві, Болдіно та на Кавказі. Скільки років жив О. С. Пушкін?

Розв’язання

Відповідь. .

Розв’язування задачі про роман О. С. Пушкіна «Євгеній Онєгін»

Задача. Вважають, що О. С. Пушкін написав роман «Євгеній Онєгін» за чотири дні. Кожного дня він писав розділів відповідно. Скільки розділів має роман «Євгеній Онєгін»?

Розв’язання

Відповідь: 8 розділів.

● Розвязування задачі вищого рівня складності:

Гуси з вирію летіли

І в зеленім лузі сіли.

Їх побачив Єлисей:

Добрий день, вам, сто гусей!

Нас не 100! – сказав вожак,

Найповажніший гусак.

Скільки ж вас? – хлопчак питає!

-Хто кмітливий – відгадає!

Якщо нас порахувати,

Й скільки є ще раз додати,

А до того половину,

ну а потім четвертину,

Та пристав би ти до нас,

То було б вже сто якраз!

Розв’язання

Відповідь: 36 гусей.

Самостійна робота із взаємоперевіркою.

Варіант 1

А)

Б)

В)

Г)

Д)

Варіант 2

А)

Б)

В)

Г)

Д)

Підведення підсумків уроку. Домашнє завдання.

О. С. Пушкін писав: «Коли малюєш обличчя людини, овал діли навпіл – одержиш лінію носа. Лобову частину ділиш навпіл – одержиш лінію очей. Нижню частину ділиш навпіл – одержиш лінію губ. Малюючи тіло людини, теж додержуйся таких пропорцій.

Висновок: Дроби використовують в малюванні

Перший ряд

Розв’яжіть рівняння

А)

Б)

Обчислити значення виразу

А)

Б)

Розв’яжіть задачу

Як відомо, О. С. Пушкін 120 років прожив у Москві, року – в Царському селі, року – в Петербурзі, року відбував заслання на Півдні, року знаходився у селі Михайлівське, року перебував у Петербурзі, Москві, Болдіно та на Кавказі. Скільки років жив О. С. Пушкін?

Розв’яжіть задачу

Вважають, що О. С. Пушкін написав роман «Євгеній Онєгін» за чотири дні. Кожного дня він писав розділів відповідно. Скільки розділів має роман «Євгеній Онєгін»?

Самостійна робота (із взаємоперевіркою)

Варіант 1

А)

Б)

В)

Г)

Д)

Варіант 2

А)

Б)

В)

Г)

Д)

Другий ряд

Розв’яжіть рівняння

А)

Б)

Обчислити значення виразу

А)

Б)

Розв’яжіть задачу

Розв’яжіть задачу

Самостійна робота (із взаємоперевіркою)

Варіант 1

А)

Б)

В)

Г)

Д)

Варіант 2

А)

Б)

В)

Г)

Д)

Третій ряд

Розв’яжіть рівняння

А)

Б)

Обчислити значення виразу

А)

Б)

Розв’яжіть задачу

Розв’яжіть задачу

Самостійна робота (із взаємоперевіркою)

Варіант 1

А)

Б)

В)

Г)

Д)

Варіант 2

А)

Б)

В)

Г)

Д)

Додаток 4

5 клас

*Тема уроку:*	Додавання і віднімання десяткових дробів.
*Мета уроку:*	Повторити та узагальнити відомості про десяткові дроби, зокрема про додавання і віднімання десяткових дробів; закріпити вміння та навички застосування цих дій до розв’язування задач; розвивати творчі здібності учнів, логічне мислення та уяву. Пробуджувати інтерес до математики.
*Обладнання:*	Плакати із завданнями, презентація, різнокольорові зірочки для оцінки знань учнів, кольорові жетони - для світлофора(сигнал зворотного зв’язку). На кожному етапі уроку сигналізують вчителю: червоний колір - не зрозумів; жовтий-зрозумів не все; зелений - все зрозумів. Портрет С. Стівена; картки індивідуального завдання учнів.
*Тип уроку:*	Узагальнення і систематизація знань.
*Девіз уроку:*	Математик так само, як і художник створює візерунки. Візерунки математика так само, як і візерунки Художника повинні бути прекрасні… У світі немає місця для некрасивої математики. Г.Г. Харді

Хід уроку:

I. Організаційний момент.

II. Мотивація навчальної діяльності учнів.

Учитель. Сьогодні ми з вами, любі діти, будемо частинами вернісажу.

Чи знаєте ви, що це таке?

(Виставка картин).

Але сьогоднішній вернісаж незвичний, він математичний і присвячений темі: «Додавання і віднімання десяткових дробів». Побувавши на вернісажі, ми узагальнимо і систематизуємо знання, вміння і навички, які стосуються цих арифметичних дій з десятковими дробами.

III. Організація навчально-пізнавальної діяльності учнів.

Історична довідка.

Відкриває вернісаж картина, батьківщина якої Єгипет.

Вона незрозуміла для пересічного глядача. Що тут зображено?

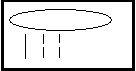$C:\Users\Юрій\Desktop\Безымянный.png$ (В стародавньому Єгипті так зображали дріб =0,2).

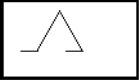
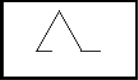$C:\Users\Юрій\Desktop\Безымянный.png$

(

$C:\Users\Юрій\Desktop\Безымянный.png$ $C:\Users\Юрій\Desktop\Безымянный.png$ (знак +) (знак - )

В Європі вчення про десяткові дроби першим виклав голландський математик та інженер. Який присвятив цьому питанню працю «Десятина»(1585 р.).

Перед вами палітрі художника. На ній кожному числу відповідає буква. Виконайте завдання і розшифруйте прізвище вченого - математика.

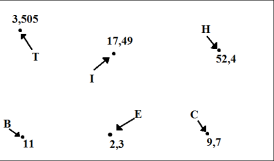$C:\Users\Юрій\Desktop\Безымянный.png$ 1). 7,43+2,27=9,7

2). 3,5+0,005=3,505

3). 42,81-25,32=17,49

4). 7,3+2,9+0,7+0,1=11

5). 8,09-4,7-1,09=2,3

6). 57,2-5,2+0,4=52,4

Номер завдання	1	2	3	4	5	6
Число
Буква

Відгадай, що зображено на картинці.

На цьому етапі необхідно розв’язати рівняння і вибрати правильну відповідь.

48,36+х=78,5	К=30,14	Р=29,15
у+0,896=1,07	О=0,174	У=1,17
х-7,36=3,04	Д=10,15	С=10,4
9-у=1,5	Н=8,2	К=7,5
0,74-х=0,25	А=0,49	Е=0,53

Учні утворюють слово «коска»

(Коска в перекладі на українську мову це – кома).

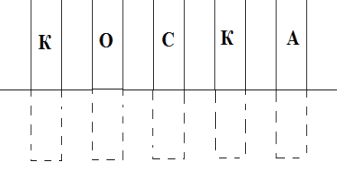$C:\Users\Юрій\Desktop\Безымянный.png$ Відомо, яке важливе значення має кома в українській мові, від неправильно поставленої коми зміст речення може суттєво змінитися.

В математиці від положення коми залежить правильність рівностей.

Доповни картинку.

Поставте в наступних рівностях кому так, щоб вони були вірними.

32+18=5	(3,2+1,8=5)
3+108=408	(3+1,08=4,08)
42+17=212	(4,2+17=21,2)
736-336=4	(7,36-3,36=4)
63-27=603	(63-2,7=60,3)
57-4=17	(5,7-4=1,7)

Запишіть їх у зошит.

Реставраційні майстерні.

На виставці є картини, які побували в реставраційних майстернях. Уявіть себе у ролі реставратора і відловіть наступні записи.

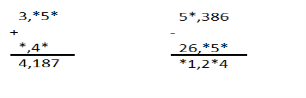
$C:\Users\Юрій\Desktop\Безымянный.png$

Порівняй

13,2+18,04 * 48,36-17,04

Дизайн вернісажного залу.

Яку площу мають дві прямокутні картини разом, якщо сторони першої картини 2,87м і 3м, а другої 1,13м і 3м?

Самостійна робота.

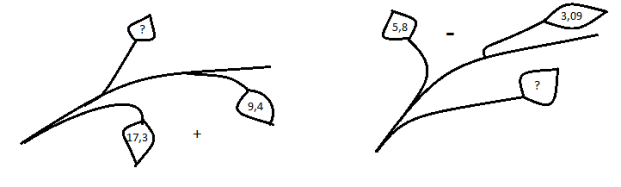
Спробуйте тепер самі «написати» математичну картину.

В-1

1) $C:\Users\Юрій\Desktop\Безымянный.png$

2) Ширина прямокутної картини 25,3м, а її довжина на 8,7м більша. Знайти довжину картини.

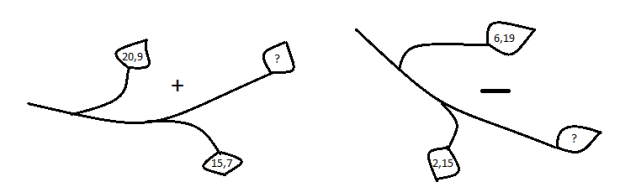
В-2

1) $C:\Users\Юрій\Desktop\Безымянный.png$

2) Довжина прямокутної картини 18,7м, а ширина на 5,3м менша. Знайти ширину картини.

IV. Підсумок уроку.

Сьогодні ми побували на виставці «Десяткові дроби» і затрималися у залі «Додавання і віднімання десяткових дробів. Значення десяткових дробів важко переоцінити.

З обчисленнями дружать,	Система мір метрична
Людині вірно служать,	Така зручна та звична,
До послуг нам готові.	Проте в її основі
Це дроби десяткові.	Є дроби десяткові.
У підручниках, предметах	Нам робить калькулятор
У журналах і газетах,	Обчислення чудові,
В повсякденній мові –	А на його екрані -
Скрізь дроби десяткові.	Теж дроби десяткові.

Корисні та практичні.

Вони нам стануть звичні.

Вивчати ми готові

Ці дроби десяткові!

Додаток 5

9 клас

Тема уроку : Прикладні задачі та їх математичні моделі. Математичне моделювання.

Мета уроку:

навчальна: продовжити знайомити учнів з прикладними задачами;

формувати вміння створювати математичні моделі прикладних задач;

розвиваюча: розвивати вміння аналізувати та описувати реальні предмети (явища) мовою математики;
виховна: формувати навички самостійної та колективної роботи.

Тип уроку: урок формування нових знань, вмінь та навичок.

Обладнання: презентація, диференційовані завдання для учнів, опорні схеми.

Хід уроку :

Організаційний момент.
Перевірка д/з за допомогою тесту.

Тест

Дописати речення:

Задачі, які ми розв’язуємо у школі, за характером своїх об’єктів бувають …
Прикладною називається задача, у якій об’єктом розгляду є …
Математичною називається задача, усі об’єкти якої …
Математичною моделлю практичної задачі називається спеціально створений об’єкт, який …
Розв’язування математичної моделі даної задачі здійснюється в 3 етапи:

Математичним моделюванням називається перехід від даної прикладної задачі до її …

Перевірка: 1 учень зачитує умову, 2 учень – відповідь. Всі учні ставлять на листках «+» або «-».

Мотивація навчальної діяльності.

Розв’язування стародавніх задач прикладного змісту.

Повідомлення теми і мети уроку.
Робота з завданнями на листках.
Домашнє завдання.

§63 № 285 ( скласти математичну модель та розв’язати задачу); № 284 (в)

Підведення підсумків уроку. Оцінювання учнів.

Старовинні задачі прикладного змісту.

У давнину в будівництві широко використовували коло і його поділ на частини. Циркуль раніше називали «шестернею». Чому?
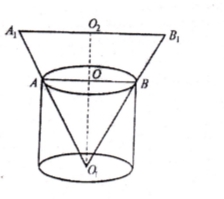
Діаметри посуду вимірювали за допомогою нутромірів. Обґрунтувати спосіб вимірювання.
Діаметри дерев лісники вимірювали за допомогою «мірної вилки». На чому ґрунтується принцип дії цього приладу?

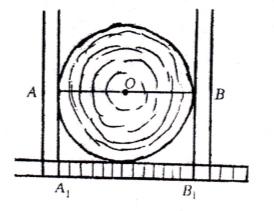
Скласти математичну модель задач:

Варіант I

А) Знайти об’єм брусу розміри якого 40 см, 30 см, 20 см.

Б) Одна бригада може виконати роботу за 3 год., друга – за 5 год. За скільки годин цю роботу вони б виконали разом?

Варіант II

А) Прямокутна ділянка землі має довжину 95 м, а ширину – 67 м. Знайти площу і периметр ділянки.

Б) Однією із двох труб басейн можна заповнити за 3 год., а другою – за 5 год. За скільки годин наповнюється басейн, якщо відкрити обидві труби?

Що спільного в цих задачах?

Розв’язати задачу за схемою:

Створення математичної моделі.
Розв’язування математичної задачі.
Інтерпретація відповіді.
Самостійна робота

Варіант I	Варіант II
Створити математичну модель та розв’язати задачу
Катер проплив 15 км за течією річки і 4 км озером, затративши на весь шлях 1 год. Знайдіть власну швидкість катера, якщо швидкість течії річки становить 4 км/год.	Моторний човен проплив 3 км проти течії річки і 12 км озером, затративши на весь шлях 1 год. Знайти власну швидкість човна, якщо швидкість течії річки 4 км/год.

Задача-проблема

Вам потрібно дійти до дверей, відстань до яких – 3 м, але виконуючи такі умови: 1-й крок дорівнює 1 м, другий - м, третій - м, і т. д., кожний наступний крок у 2 рази менший від попереднього. Чи вдасться вам це зробити?

Додаток 6

	5 клас
*Тема уроку:*	Площі прямокутника і квадрата

Хід уроку:

I. Організаційний момент.

II. Перевірка домашнього завдання.

№582

Р=162 дм	1)162-2
а=47 дм	2)68-друга ст..
S -?	3) S=4734=1598 (дм²)

№588

340000 м²=34 га	53 км²=53000000 м²=5300 га
5830000 м²=583 га	14 км²=1400 га
5 км² 18 га=5000000 м²+ 180000 м²=518 га
24 км² 6 га=2400 га + 6 га=2406 га

III. Актуалізацыя опорних знань учнів. Колективне розв’язування вправ для усного рахунку.

Виразити у м²:
7 га=70000 м²	П
14 га=1400 м²	Л
60000 см²=6 м²	О
Знайти S□ зі стороною 4 см	Щ
Знайти Р зі сторонами 4 см і 5 см	А

Л	О	П	А	Щ
1400 м²	6 м²	70000 м²	20 см²	16 см²

IV. Мотивація навчальної діяльності учнів.

Історична довідка.

Виникнення поняття «площа» земельної ділянки в Стародавньому Єгипті.

Повідомлення теми і мети уроку.

V. Розв’язання задач і вправ.

Поділ 3чнів класу на II групи.

Виконання практичного завдання.

В-1	В-2
а)Вибрати із набору фігур прямокутник і квадрат.	а)Вибрати із набору квадрат і прямокутник.
б)Виміряти сторони і обчислити площу прямокутника.	б)Виміряти сторони і площу квадрата.

(взаємоперевірка)

Розв’язування задач

№2	№2
а=500 м	1 м²-180 г
b=400 м	а=6 м
1 га - 260 кг	b=3 м
S-?	S-?
Чи вистачить 5 т гор.	Чи вистачить 3 кг фарби.
1). 500400=20000=20 га	1). 6 3=18 (м²)
2). 20260=5200 (кг)=5 т 200 кг Відповідь:5 т не вистачить.	2).18 180=3240 (г)=3 кг 240 г Відповідь:фарби не вистачить.

VI. Підведення підсумків уроку.

Бліц-турнір.

VII. Оцінювання учнів.

VIII. Домашнє завдання:

Розв’язати завдання протилежного варіанту. Побудувати прямокутник і квадрат, Р яких рівні. Зробіть висновок про площі.

$C:\Users\Юрій\Desktop\Antonio_Basoli_Ancient_Egyptian_Architecture_Figurative_art_Representational_art_Pyramids_Temples_Architecture_b.jpg$

I група «Юні агрономи»

Обчислити площу посівної ділянки, зображеної на малюнку:

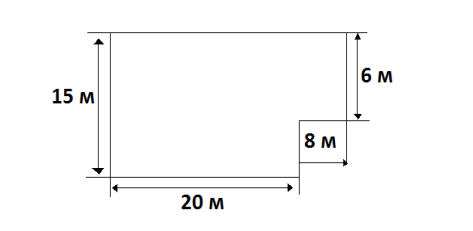
$C:\Users\Юрій\Desktop\Безымянный.png$

Чи вистачить 5 т гороху, щоб засіяти ним поле, що має форму прямокутника зі сторонами 500 м і 400 м, якщо на 1 га землі треба висіяти 260 кг гороху?
Поле квадратної форми має площу 36 га. Обчислити периметр поля.

Бліц-турнір

Чи згодні ви з твердженням:

а). рівні фігури мають рівні площі?

б). нерівні фігури мають різні площі?

в). будь який квадрат є прямокутником?

$C:\Users\Юрій\Desktop\Antonio_Basoli_Ancient_Egyptian_Architecture_Figurative_art_Representational_art_Pyramids_Temples_Architecture_b.jpg$ г). деякі прямокутники є квадратами? Які саме

II група «Юні будівельники»

Обчислити площу посівної ділянки, зображеної на малюнку:

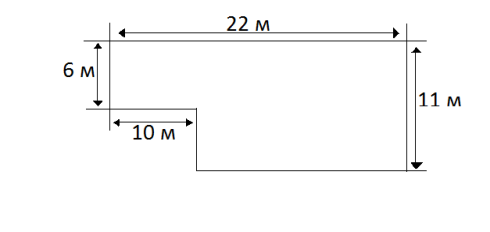$C:\Users\Юрій\Desktop\Безымянный.png$ Витрати емалевої фарби ПФ-115 на одношарове покриття становлять 180 г на м². Чи вистачить 3 кг емалі, щоб пофарбувати стіну довжиною 6 м і висотою 3 м?
Довжина кімнати 8 м, ширина - 6 м, учнів у класі -24. Яка площа припадає на 1 учня?

Бліц-турнір

Чи згодні ви з твердженням:

а). рівні фігури мають рівні площі?

б). нерівні фігури мають різні площі?

в). будь який квадрат є прямокутником?

г). деякі прямокутники є квадратами? Які саме?

Додаток 7

10 клас

Хіміко-математичний КВК

«Розумники та розумниці»

Мета: зацікавити учнів математикою та хімією, показати взаємозв’язок цих наук; заохочувати учнів до здобуття нових знань, формувати вміння працювати в команді, розвивати кмітливість, логіку, пам'ять.

План проведення

Слово ведучого (знайомство з командами та журі)
Конкурс «Розминка»(командам пропонується по 30 запитань; на обміркування – 10 с; за кожну правильну відповідь – 1 бал)
Конкурс «Назвіть учених» (командам пропонується по 3 запитання; на обміркування – 15 с; за кожну правильну відповідь – 2 бала)
Конкурс «Ваш вихід, капітани» ( на обміркування – 30 с; за кожну повну відповідь – 4 бали)
Конкурс «Гонка за лідером» (кожна команда за 3 хв повинна відповісти на якомога більшу кількість запитань; максимальна кількість запитань – 10; за кожну правильну відповідь – 1 бал)
Конкурс «Азартна дюжина» (командам пропонується по 12 запитань; на обміркування – 10 с; за кожну правильну відповідь – 1 бал)
Підбиття підсумків та нагородження переможців.

Зміст конкурсів

Конкурс «Розминка»

Команда «Веселящий газ»

Запитання:

Проста речовина, утворена гідрогеном (водень)
Основа прямокутного паралелепіпеда (прямокутник)
Речовина, що прискорює реакцію, але не використовується при цьому (каталізатор)
Рівняння, в яких невідоме міститься під знаком кореня (ірраціональне)
Реакція взаємодії з киснем (окислення)
Який знак має корінь непарного степеня з додатного числа? (+)
Реакція окислювання з виділенням тепла і світла (горіння)
Який знак має корінь непарного степеня з від’ємного числа? (-)
Один з продуктів розпаду калій перманганату, проста речовина (кисень)
Основа трикутної піраміди (трикутник)
Реакції,внаслідок яких із однієї речовини утворюється кілька (розкладу)
Правильний багатогранник, у якого всі грані квадрати (куб)
Реакції,внаслідок яких утворюється одна речовина (сполучення)
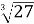(3)
Речовина, що підтримує дихання та горіння (кисень)
Прямі в просторі, що не перетинаються і не паралельні (мимобіжні)
Речовина, що використовується для різання й зварювання тугоплавких металів (водень)
Сума вертикальних кутів ()
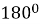Проста речовина з молярною масою 48 (озон)
Сума кутів чотирикутника ()
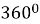Найлегший газ (водень)
Добуток декількох однакових множників (степінь)
Одиниця кількості речовини (моль)
Перша російська назва цього елемента «водураздающий» (Гідроген)
Якою буквою позначається множина цілих чисел (Z)
Елемент, про який в народі кажуть: метал – і плуг у полі, і цвях у домі (Ферум)
Степінь квадратного рівняння (2)
Газ, що називають «газом життя» (кисень)
Рівняння лінійної функції ()
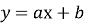Процес хімічного перетворення вуглекислого газу в кисень (фотосинтез)

Команда «Карбон»

Запитання:

Cторони прямокутного трикутника, що лежить проти прямого кута (гіпотенуза)
Газ, що уперше «знайшли» на Сонці (гелій)
Протилежні кути, що утворюються при перетині двох прямих (вертикальні)
Основний компонент повітря (азот)
Наближене значення числа π (3,14)
Газоподібна речовина, що руйнує озоновий шар (фреон)
Основа паралелепіпеда (паралелограм)
Відрізок, що з’єднує центр кола з будь-якою його точкою (радіус)
Рідкий метал (ртуть)
Сума кутів трикутника ()
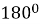Проста речовина з молярною масою 2 (водень)
Чотирикутник, у якого дві протилежні сторони паралельні, а дві ні (трапеція)
Одиниця вимірювання молярної маси (г/моль)
Промінь, що виходить із вершини кута і ділить його навпіл (бісектриса)
Реакція між простою й складною речовиною (заміщення)
Степінь біквадратного рівняння (4)
Учений, що відкрив закон збереження маси речовини ( Ломоносов)
Відрізок, що з’єднує вершину трикутника й середину протилежної їй сторони (медіана)
Сповільнює реакцію (інгібітор)
Рівняння параболи ()
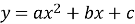Розкладання речовини електричним струмом (електроліз)
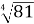(3)
Сам не горить, а підтримує горіння (кисень)
У яких одиницях виміряється площа фігури ()
Вода у твердому стані (лід)
Дві прямі, паралельні третій прямій …
Найпоширеніший елемент космосу (гідроген)
Назва першого теоретичного трактату з математики («Начала»)
Газ у газованій воді (вуглекислий)
Одиниці вимірювання об’єму

Конкурс «Назвіть учених»

Команда «Веселящий газ»

Запитання:

Хто відкрив періодичний закон і запропонував періодичну систему елементів? (Д.І.Менделєєв)
Хто перший написав теоретичну працю з математики «Начала»? (Евклід)
Хто був першою жінкою-професором математики? (С.Ковалевська)

Команда «Карбон»

Запитання:

Хто створив теорію будови органічних сполук? (А.М.Бутлеров)
Хто відкрив закон збереження маси речовини? (Ломоносов і Лавуазьє)
Хто створив перший друкований підручник з математики? (Л.Ф.Магницький)

Конкурс «Ваш вихід, капітани!»

Завдання:

Замініть назви хімічних елементів відповідними словами:

Не те все Аурум, що блищить. (золото)
Ферумний характер.(залізний)
Слово Аргентум, а мовчання Аурум. (срібло,золото)
Пройшов вогонь, воду і Купрумні труби. (мідні)

Конкурс «Гонка за лідером»

Команда «Веселящий газ»

Запитання:

Який елемент є найбільш електропровідним ? (Аргентум)
Який елемент є найбільш пластичним ? (Аурум)
На який хімічний елемент є багатою морська капуста ламінарія? (Йод)
Назва якого хімічного елемента є співзвучною з російською назвою соснового лісу? (Бор)
Назва якого хімічного елемента походить від однієї з планет сонячної системи? (Нептуній)
Який радіоактивний елемент названо на честь Польщі? (Полоній)
Які елементи називають «хімічними лінивцями»? (інертні гази)
Цей метал називають металом роз корзини або «ювелірною королевою» (платина)
Якою за рахунком дитиною в сім’ї був Д.І.Менделєєв? (сімнадцятою)
Який елемент використовується в лікуванні: незначна кількість цього елемента, розчиненого в лікувальних грязях, благотворно впливає на нервові закінчення, що є в шкірі? (Радон)

Команда «Карбон»

Запитання:

Який метал має бактерицидні властивості? (Срібло)
Який метал використовується в хірургії для скріплення уламків кісток? (Тантал)
Назва якої акваріумної рибки є співзвучною з назвою хімічного елемента? (Неон)
Який елемент називають «жовчю бога Вулкана»? (Сульфур)
Який метал називають і чому «хімічним хижаком»? (Сурму, бо вона розчиняє і «пожирає» майже всі метали)
Який металічний елемент входить до складу гемоглобіну крові? (Ферум)
Який метал за нормальних умов є рідким? (Гідраргірум)
Без якого металу неможлива фотографія? (Срібло)
Який елемент називають «елементом думки і розуму»? (Фосфор)
Як називається найдрібніша, хімічно неподільна частинка речовини? (Атом)

Конкурс «Азартна дюжина»

Команда «Веселящий газ»

Запитання:

Цю речовину Леонардо да Вінчі називав «соком життя» (вода)
Степінь з дробовим показником можна замінити…(радикалом)
Цей метал одночасно називають «мерзським», «сатанинським», але разом з тим і «божественним» (золото)
Сума квадратів катетів у прямокутному трикутнику дорівнює (квадрат гіпотенузи)
Його називають «царем» живої природи, «основою життя» і «хлібом рослин» (карбон)
Скільки градусів представляють π радіан ()
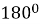Д.І.Менделєєв називав його «чорним металом» (вугілля)
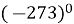(1)
«Цар неживої природи» (силіцій)
Як називається радикали, які мають рівні підкореневі вирази і однакові показники? (подібні)
У часи Петра Великого цю кислоту називали «міцною горілкою» (нітратна)
Область визначення функції – це безліч значень аргументу х або безліч значень функції у (безліч значень аргументу х)

Команда «Карбон»

Запитання:

Цей газ у великих концентраціях збуджує нервову систему і діє як наркотик, звідси й назва («закис азоту» - нітроген(!) оксид)
Як розміщуються прямі в просторі (паралельні, перетинаються, співпадають, мимобіжні)
Цей метал називають металом роз корзини або «ювелірною королевою» (платина)
Область значень функції 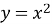; [0;+∞)
Скільки досить прямих на площині, щоб пряма, що не належить площині, проходила через точку їхнього перетину й була перпендикулярною до всієї площини? (дві)
Одне з самих титулованих корисних копалин – «королева енергетики» , «королева копалин». Раніше її називали «зеленим маслом», а в часи Бориса Годунова «густою водою, що горить» (нафта)
Формула дискримінанта квадратного рівняння ()
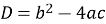Що є графіком функції 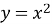(парабола)
За здатність цієї речовини світитися в темряві алхімік Бранд назвав його «холодним вогнем» (білий фосфор)
Метал, що став причиною загибелі антарктичної експедиції Скотта в 1912 році (олово)
Як визначити, що квадратне рівняння не має коренів, не розв’язуючи його (D<0)
Метал, що перетворює скло в кришталь (свинець - плюмбум)

Додаток 8

Вчитель: Ясевіна Т. Т.

8 клас

Тема уроку: Додавання і віднімання дробів з однаковими знаменниками.

Мета уроку: удосконалити вміння додавати і віднімати дроби з однаковими знаменниками.

1)навчальна: дроби з однаковими знаменниками.

2)розвивальна: розвивати уважність, формувати критичне мислення, вміння аналізувати умову завдання.

3)виховна: виховувати вміння працювати самостійно, в групі та в колективі.

Тип уроку: урок удосконалення знань, вмінь та навичок учнів.

Хід уроку:

І. Організаційний момент. Рефлексія.

ІІ. Повідомлення теми, мети уроку.

ІІІ. Актуалізація опорних знань учнів.

-Сформулюйте правила додавання і віднімання дробів з однаковими знаменниками (фронтально)

-Усні вправи (з елементами історії) на екрані.

●Дізнайтеся прізвище видатного англійського вченого. Для цього виконайте дії з виразами на екрані та перенесіть букви, що відповідають результатам у другу таблицю. Яке прізвище ви отримали?

а) (ю) б) (ь) в) (н)

г) (о) д) (т) е) (н)


н	ь	ю	т	о	н

Відомий англійський вчений Ісаак Ньютон (1643-1727) своїй монографії "Універсальна арифметика" (1707) розглядає не тільки звичайні дроби, а й раціональні та дії над ними. Також раціональні дроби та дії з ними розглянув у своїй праці "арифметика" давньогрецький математик Діофант (бл. ІІІ ст. н.е.). На сторінках цієї книги можна зустріти доведення тотожностей.

ІV. Удосконалення вмінь та навичок дій з раціональними дробами.

●Робота у парах (див. додаток).

V. Перевірка знань. (самоперевірка)

1. В)

2. Б)

3. В)

4. Б)

5. Б)

6. Б)

VІ. Підсумки уроку (слайд). Знайти помилку на екрані.

VІІ. Оцінювання учнів.

Усн. впр.	0,5б.
№1	3б.
№2	0,5б.
№3	0,5б.
№4	0,5б.
№5	0,5б.
№6	0,5б.
Тест	6б.

VІІІ. Домашнє завдання: №72(3, 4);

№77(2);

№84(1, 2);

Підготуватись до вивчення нового матеріалу.

12.Список використаних джерел

Звєрєва Г., Сердюк В. Компетентнісний підхід до навчання учнів на уроках математики. Математика в школах України. №9/2010.
Возна М. спроби формування цілісної картини навколишнього світу в процесі навчання математики. Математика в школах України. №30/2005
Козак Л.М. Виховання національної свідомості на уроках математики. Математичний вісник. Науково – методичний збірник. Випуск 3. Чернівці. 2005.
Тимофійчук О. Математика на службі екології. Математичний вісник. Науково – методичний збірник. Випуск 3. Чернівці. 2005.
Панішева О. Класики допомагають вивчати теорію ймовірностей. Математика. №7/2006.
Б.Орач. Математичні моделі як засіб інтеграції знань. Математика №11, березень 2002р.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Ясевіна Тетяна Тимофіївна

Пов’язані теми

Математика, 11 клас, Методичні рекомендації

Додано

29 квітня 2022

Переглядів

3695

Оцінка розробки

Відгуки відсутні