Методичні рекомендації "Розв'язування задач графічного змісту"
У навчально-методичному посібнику розглянуто задачі, які передбачають побудову або аналіз графічних зображень. Вони тісно пов'язані з усією методичною системою навчання алгебри, є її органічною частиною
Система задач узгоджується з основними дидактичними принципами.
Найдоцільніше створювати системи графічних задач до кожної теми, хоча розв'язування деяких з них вимагає комплексного застосування кількох тем.
Методичні рекомендації
щодо розв’язування задач графічного змісту
Галайчук Марія Григорівна,
вчитель математики
![]()
У навчально-методичному посібнику розглянуто задачі, які передбачають побудову або аналіз графічних зображень. Вони тісно пов’язані з усією методичною системою навчання алгебри, є її органічною частиною
Система задач узгоджується з основними дидактичними принципами.
Найдоцільніше створювати системи графічних задач до кожної теми, хоча розв’язування деяких з них вимагає комплексного застосування кількох тем.
![]()
Зміст
|
Вступ…………………………………………………………………. |
4 |
|
Розділ І. Задачі графічного змісту………………….………………. |
5 |
|
5 |
|
7 |
|
15 |
|
Розділ ІІ. Графіки функцій пов’язаних із символами max і min…. |
32 |
|
Розділ ІІІ. Задачі графічного змісту з теми: «Тригонометричні функції».………………………………….…..… |
49 |
|
Висновки………………………………..………………………..….. |
65 |
|
Список використаних джерел…..……………………………..…… |
66 |
![]()
![]() Вступ
Вступ
Під задачами графічного змісту з алгебри розуміють задачі, що передбачають побудову або аналіз графічних зображень.
Усі задачі поділено на три класи відповідно до графічної інтерпретації:
- задачі з графічною презентацією умови;
- задачі з графічною презентацією вимоги;
- задачі у яких графічна інтерпретація з’являється під час розв’язання та обґрунтування і є допоміжним засобом.
Опрацювавши наведені приклади учні можуть закріпити своє знання і вміння за допомогою тренувальних вправ та використати їх для підготовки до державної підсумкової атестації та ЗНО в 11 класі.
Р о з д і л І
Задачі ГРАФІЧНОГО змісту
- Задачі з графічною презентацією умови
- [1; «о).
-
(-«<>; 1].
Відповідь. А.
Б. (-t 5]. Г. [4: -).
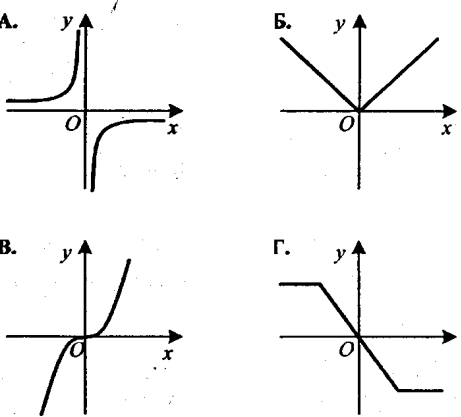
6 (9). На одному з малюнків зображено 4
графік функцій у = — . Укажіть цей малюнок. х
Відповідь. В.
11 (І2). На малюнку зображено графік функції у=/{х), визначеної на множині дійсних чисел. Користуючись малюнком, установіть множину розв’язків нерівності Дх) > 0.
- (-1; 3). Б. (-3; 2).
- (-«>; 4)U(3; <*>). Г. (-°°; —4)U(—1; 3).
Відповідь. Г.
32 (б). На малюнку зображено графік руху туриста, де s км — відстань, яку пройшов турист за t год. Скільки часу тривав відпочинок туриста?
Розглянемо різні типи таких задач, наведених у першій частині атестаційної роботи.
Тестові завдання
Виберіть правильну відповідь серед запропонованих.
1). На малюнку зображено графік функції у =-x2+2х+4. Користуючись малюнком, установіть проміжок спадання функції.
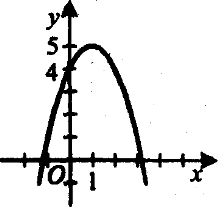
А. [1; ∞). Б.(-∞;5].
Б. ( -∞; 1]. Г. [4: ∞).
Відповідь. А.
2). На одному з малюнків зображено 4 графік функцій у =![]() . Укажіть цей малюнок.
. Укажіть цей малюнок.
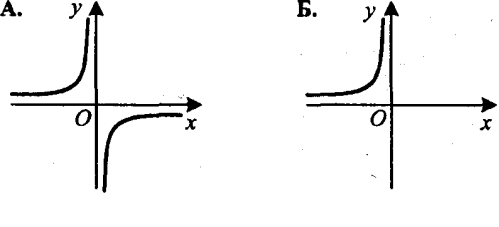
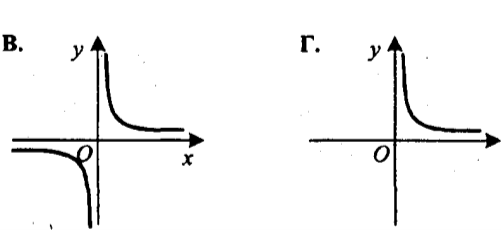
Відповідь. Б.
3). На малюнку зображено графік функції у=f(х), визначеної на множині дійсних чисел. Користуючись малюнком, установіть множину розв’язків нерівності f(х)>0.
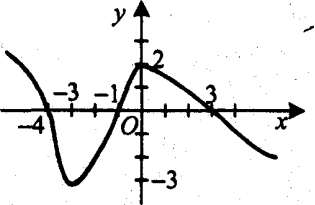
А. (-1; 3). Б. (-3; 2).
В. (-∞; 4)U(3; ∞). Г. (-∞; —4)U(-1; 3).
Відповідь. Г.
4). На малюнку зображено графік руху туриста, де sкм – відстань, яку пройшов турист за tгод. Скільки часу тривав відпочинок туриста?
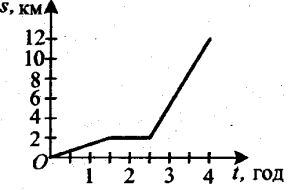
А. 0,5 год. Б. 1 год.
Б. 1,5год. Г. 2 год.
Відповідь. Б.
5). На якому з малюнків зображено графік парної функції?
Відповідь. Б.
- Задачі з графічною презентацією вимоги
Такі задачі відповідають достатньому і високому рівням навчальних досягнень, а тому потребують окремої уваги під час підготовки учнів до ДПА. Один з типів таких задач – це задачі на побудову графіка функції, за допомогою якого необхідно визначити множину значень, проміжки монотонності або знакосталості. Інший тип задач – це задачі на побудову графіків рівнянь.
Розв’язуючи такі задачі, учні повинні усвідомлювати, що побудувати графік функції – означає нанести на площину всі вказані точки. Але, якщо область визначення містить нескінченно багато точок, а ми будемо зустрічатися саме з такими випадками, то нанесення всіх таких точок неможливе. На практиці роблять інакше. Наносять на площину не всі точки графіка, а лише деякі з них, а потім сполучають їх плавною лінією. Такий спосіб побудови в багатьох важливих випадках дає достатньо точний графік.
Графічне представлення функції дає можливість побачити більшість її властивостей.
1). Побудуйте графік функції у=-х2-6х-5. Користуючись графіком, знайдіть:
- множину значень функції;
- проміжок, на якому функція спадає.
Розв'язання
Графіком функції у=-х2-6х-5 є парабола, вітки якої напрямлені вниз. Знайдемо координати вершини параболи:
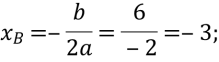
![]()
Точка (-3; 4) є вершиною даної параболи. Знайдемо абсциси точок перетину графіка функції з віссю Ох:
-хг-6х-5 = 0,
х1=-5, х2 =-1.
Вісь ординат графік цієї функції перетинає в точці (0; -5). Побудуємо графік заданої функції.
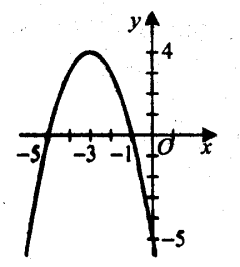
З малюнка видно, що:
- Множиною значень функції є проміжок (-∞; 4].
- функція спадає на проміжку [-3; ∞).
Відповідь. 1) (-∞; 4]; 2) [-3; ∞).
2). Побудуйте в одній системі координат графіки функцій у=![]() іу=6-х. За допомогою графіків укажіть значення x, при яких значення функції у=
іу=6-х. За допомогою графіків укажіть значення x, при яких значення функції у=![]()
Розв’язання
Побудуємо графіки функцій. Вони перетинаються в точці А(4; 2).
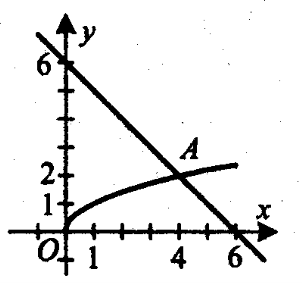
З малюнка видно, що значення функції у=6-х більші за значення функції у=![]() на проміжку [0; 4).
на проміжку [0; 4).
Відповідь. [0; 4).
3). Не виконуючи побудови, знайдіть координати точок перетину графіків функційу=5-х2іу=х-1. Накресліть графіки даних функцій і позначте знайдені точки.
Розв’язання
Для знаходження координат точок перетину графіків даних функцій розв’яжемо рівняння:
5-х2=х-1,
х2+х-6=0,
х1=-3, х2=2
Тоді х1=-4,у2 = 1.
Отже, графіки вказаних функцій перетинаються в точках (-3; -4) і (2;1).
Графіком функції у=5-х2 є парабола, вітки якої напрямлені вниз, а вершиною її є точка (0; 5).
Координати точок перетину параболи звіссю Ох=(-![]() ) і (
) і (![]() ; 0).Графікомфункції у =х-1 є пряма, що проходить через точки (0; -1), (1; 0). Накреслимо графіки даних функцій і позначимо точки їх перетину.
; 0).Графікомфункції у =х-1 є пряма, що проходить через точки (0; -1), (1; 0). Накреслимо графіки даних функцій і позначимо точки їх перетину.
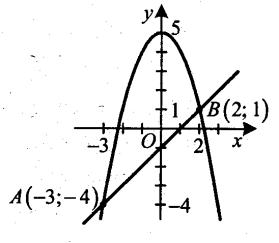
Відповідь. (-3; -4); (2; 1).
4). Побудуйте графік функції
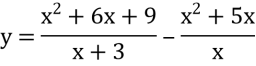
Розв’язання
Область визначення даної функції
D(y) = (-∞; -3)U(-3; 0)U(0; ∞).
Виконаємо перетворення на області визначення.
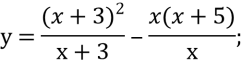
y=x+3-x-5;
y=-2.
Графіком даної функції є пряма без точок з координатами (0; -2) і (-3; -2).
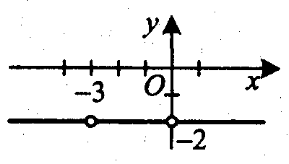
5). Побудуйте графік функції
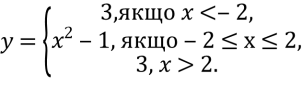
Розв’язання
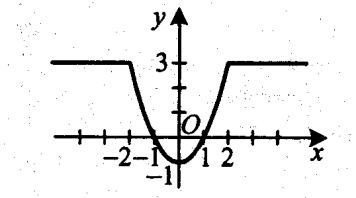
Графіком даної функції є сукупність двох півпрямиху=3, х<-2 іу=3, х>2 та частини параболи у=х2-1, -2≤ х ≤ 2 , з вершиною у точці (0; -1) та вітками, напрямленими вгору. Накреслимо цей графік.
6). Побудуйте графік рівняння
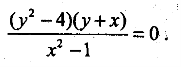
Розв’язання
Дане рівняння рівносильне такій системі:
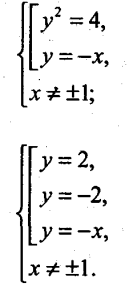
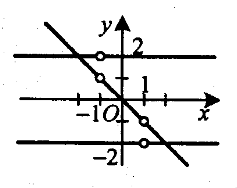
Графіком заданого рівняння є сукупність трьох прямих у=2, у=-2, у=-х без точок, абсциси яких дорівнюють 1 і -1.
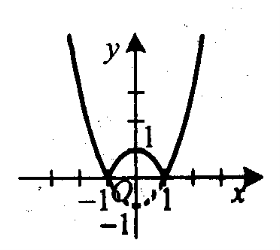
7). Побудуйте графік функції
![]()
Розв’язання
![]() =
=![]()
Побудуємо графік функції у=х2-1 – параболу, вітки якої напрямлені вгору, з вершиною в точці (0; -1). Потім ту частину графіка, що відповідає від’ємним значенням функціїу=х2-1 відобразимо симетрично відносно осі абсцис. У результаті таких перетворень отримаємо графік заданої функції.
8). Побудуйте графік рівняння
|у-х-1| = |у+х|
Розв’язання
Дане рівняння рівносильне сукупності двох рівнянь:
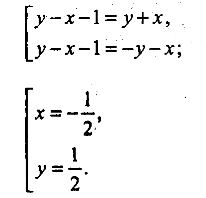
Зобразимо на координатній площині пару прямих ![]() та
та ![]() , що є графіком заданого рівняння.
, що є графіком заданого рівняння.
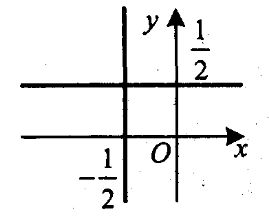
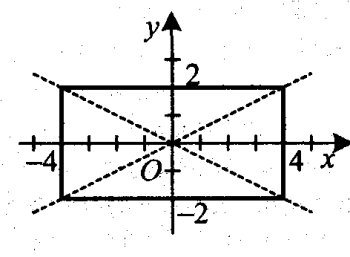
9). Побудуйте графік рівняння
|х-2у|+|х+2у| = 8.
Розв’язання
Дане рівняння рівносильне сукупності чотирьох систем.
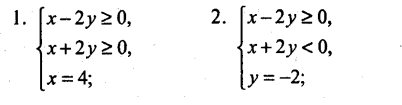
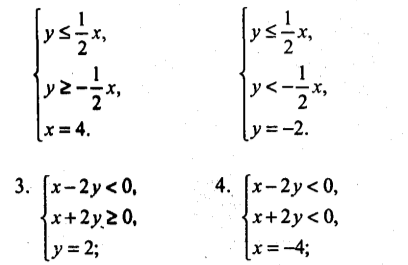
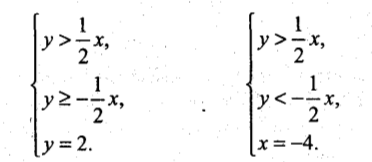
Зобразимо графік заданого рівняння.
10). Побудуйте на координатній площині множину точок, координати (х; у) яких задовольняють рівність
![]()
Розв’язання
Задане рівняння рівносильне системі.
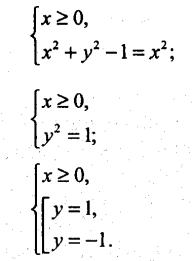
Зобразимо на координатній площині дві півпрямі, що є множиною шуканих точок.
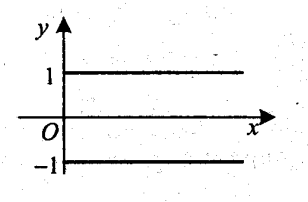
- Задачі у яких графічна інтерпретація з’являється під час розв’язання та обґрунтування і є допоміжним засобом
Такі задачі пропонуються для класів з поглибленим вивченням математики. У своїй більшості це задачі з параметрами.
Для знаходження параметра а можна виділити два основні графічні прийоми: побудова графічного образу на координатній площині хОу і на площині хОа.
1. На площині хОу функція у=f(х;а) задає сім’ю кривих, що залежать від параметра а. В першу чергу нас цікавить, за допомогою якого перетворення площини можна перейти від однієї кривої сім’ї до іншої. У запропонованих задачах використовується паралельне перенесення площини.
2. На площині хОа будується графічний образ a=f(x).Перетинаючи побудований графік прямими, перпендикулярними до параметричної осі, одержуємо потрібну інформацію.
1). Скільки коренів має рівняння |хг -4|х||=а залежно від параметра а?
Розв’язання
Зобразимо на координатній площині хОа всі точки, координати яких задовольняютьрівняння а = |хг -4|х||.
Для цього побудуємо параболу а=хг-4х=(х-2)2-4 з вершиною в точці (2;-4) і вітками, напрямленими вгору, і виконаємо послідовно два перетворення графіка так само, як у задачах, описаних вище.
Кількість коренів при кожному фіксованому значенні параметра а дорівнює кількості точок перетину зображеного графіка з горизонтальною прямою, яка відповідає цьому значенню параметра.
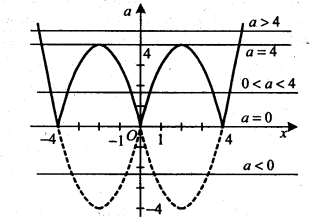
Очевидно, якщо а< 0, рівняння не має коренів; якщо а=0, рівняння має 3 корені; якщо 0<а<4, рівняння має 6 коренів; якщо а=4, рівняння має 4 корені; якщо а>4, рівняння має 2 корені.
Відповідь. Якщо а<0, то п=0; якщо а=0, то п=3; якщо 0<а<4, то п=6; якщо а=4, то п=4, якщо а>4, то п=2, де п — кількість коренів заданого рівняння.
2). При яких значеннях параметра а система
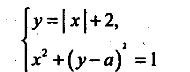
має три розв’язки?
Розв’язання
Зобразимо графіки рівнянь у=|х|+2 і х2+(y-)2=1 у системі координат хОу.
Графіком рівняння у=|х|+2 є частини прямих у=х+2 та у=-х+2, зображені на малюнку.
Графіком рівняння x2+(y-a)2=1є сім’я кіл з центрами в точках (0; а) і радіусами 1.
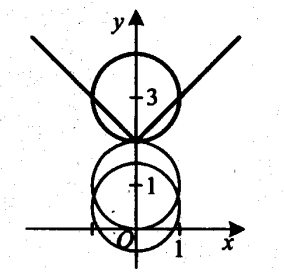
З малюнка видно, що коли а=3, графіки заданих у системі рівнянь мають три спільні точки, отже, система має три розв’язки.
Відповідь.а=3.
Розглянемо ще один тип задач, під час розв’язування яких ми не будемо зображати графіки, але при обґрунтуванні врахуємо графічну інтерпретацію об’єктів задачі.
3). При яких значеннях параметра а система рівнянь
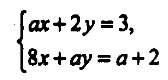
не має розв’язку?
Розв’язання
Графіками рівнянь, що входять у систему, є прямі. Щоб система не мала розв’язків, прямі мають бути паралельними. Тобто повинна виконуватися умова
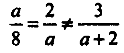
Ця система рівносильна системі
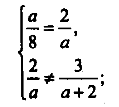
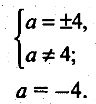
Отже, якщо а=-4, система рівнянь не має розв’язку.
Відповідь.а=-4.
4). Розв’язати графічно рівняння
![]() (1)
(1)
Розв’язання
Знаходимо корені квадратного тричлена ![]() . Маємо
. Маємо![]() , х2=2. Якщо
, х2=2. Якщо 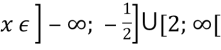 ,торівняння можна записатиу вигляді
,торівняння можна записатиу вигляді![]() або, що те саме,
або, що те саме,
а=2х2+2,5х-1; (2)
якщо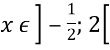 , то рівняння (1) запишеться так:
, то рівняння (1) запишеться так:
а=5,5+1 (3)
Побудуємо графік функції (2) в системі координат хОа(Рис. 1.1).
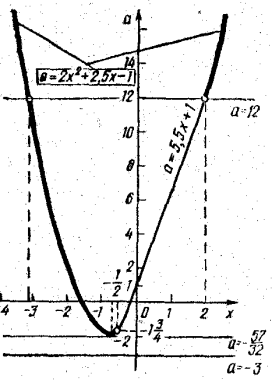
Рис. 1.1
Для 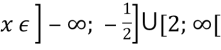 цей графік збігається з частинами параболи (на рисунку вони зображені товстими лініями), вершина якої знаходиться в точці
цей графік збігається з частинами параболи (на рисунку вони зображені товстими лініями), вершина якої знаходиться в точці 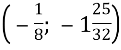 . Якщо
. Якщо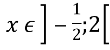 , то цей графік збігається з відрізком прямої а=5,5х+1,
, то цей графік збігається з відрізком прямої а=5,5х+1,
Як же знайти корені рівняння
z(х;а)=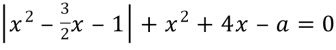
при фіксованому а? Для цього треба провести через точку (O; а) пряму паралельну осі Ох, і знайти точки перетину її з графіком функції z(х; а)=0; абсциси цих точок є коренірівняння (1), 3 рисунка бачимо, що при ![]() дане рівняннямає тільки один дійсний корінь. Якщо
дане рівняннямає тільки один дійсний корінь. Якщо ![]() ,то рівняннязавжди має два дійсних корені, при
,то рівняннязавжди має два дійсних корені, при ![]() рівняння не маєдійсних коренів.
рівняння не маєдійсних коренів.
5). Розв’язати графічно нерівність
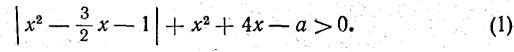
Розв’язання
Геометричним образом рівняння
z(х; а)=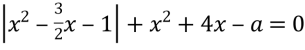
є лінія (рbс. 1.1), яка поділяє координатну площину на дві області, в кожній з яких функція z(х; а) зберігає знак. Знайдемо знак функції z(х; а) в початку координат z(0; 0)=1>0. Отже, геометричним образом множини розв’язків нерівності (1) буде область, яка знаходиться нижче від лінії z(х; а)=0 (крім точок границі області).
6). Розв’язати рівняння
![]() (1)
(1)
Розв’язання
Рівняння (1) еквівалентне таким системам:

Якщо a=0, то з рівняння (1) маємо х=0, тобто дане рівняння має єдиний розв’язок. При а≠0 із системи (2) дістаємо: якщо а≥1, то ![]() . Щоб знайти корені рівняння (1)при фіксованому а, проводимо через відповідну точку на осі Оапряму, паралельну осі Ох. Абсциси точок перетинуцієї прямоїз графіком параболи
. Щоб знайти корені рівняння (1)при фіксованому а, проводимо через відповідну точку на осі Оапряму, паралельну осі Ох. Абсциси точок перетинуцієї прямоїз графіком параболи ![]() і будуть коренями рівняння (1) (рис. 1.2).
і будуть коренями рівняння (1) (рис. 1.2).
7). Розв’язати нерівність
![]() (1)
(1)
Розв’язання
Дана нерівність рівносильна таким системам нерівностей:
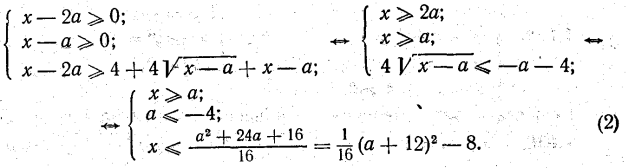
Із системи (2) маємо: a≤-4, то а≤![]() (а+12)2-8.
(а+12)2-8.
Область, заштрихована сіткою на рис. 1.3, дає множину пар (х; а), які задовольняють нерівність (1). Щоб дістати розв’язок нерівності (1) при певному значенні а, проведемо через точку (О; а) пряму, паралельну осі Ох. Абсциси точок відрізка цієї прямої, які знаходяться в заштрихованій сіткою області, і будуть розв’язками нерівності (1) при заданому значені параметра а.
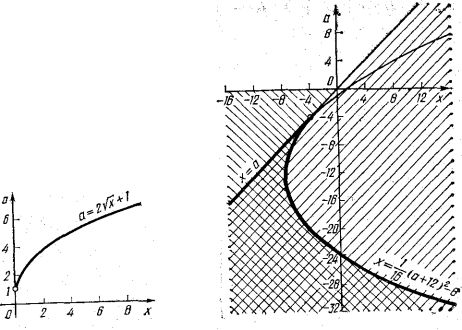
Рис. 1.2 Рис. 1.3.
8). Для якого найбільшого цілого значення параметра а рівняння ||x-4|-a|=11 має два розв’язки?
Розв’язання
Розв’яжемо рівняння графічним способом.
Дане рівняння має два розв’язки, коли графіки функцій
f(x)=11та g(x)=||x-4|-a|
перетинаються у двох точках.
Графіком функції f(х) =11 є пряма, яка паралельна осі Ох і проходить через точку (0; 11).
Розглянемо різні положення графіка функції g(x) =||х– 4|-a| залежно від значення параметра а та визначимо кількість точок перетину графіків f(х) та g(x).
1. Якщо а=0, g(x)=g1(x) =|х-4|.
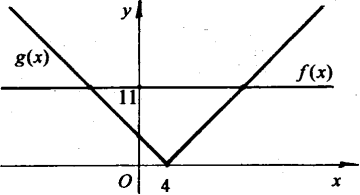
Графіки перетинаються у двох точках, тому рівняння має два розв’яжи.
2. Якщо а<-11, графік функції g(x) можна отримати з графіка g1(х) паралельним перенесенням вздовж осі Оу на |а|одиниць вгору.
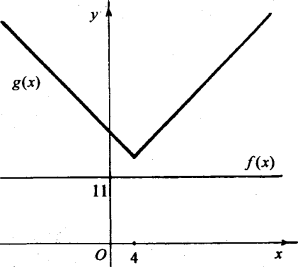
У даному випадку точок перегину немає. Рівняння розв’язків немає.
3. Якщо а=-11, маємо одну точку перетину графіків g(x)і f(х).
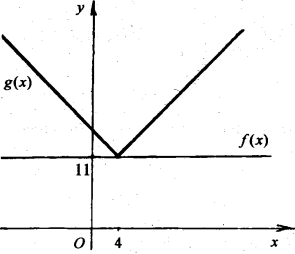
4. Якщо -11<а<0, графіки функцій f(x)і g(x)перетинаються у двох точках і рівняння має два розв’язки.
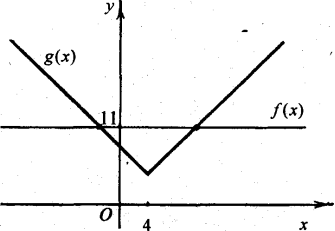
5. Якщо 0<а<11, графік функції g(x) можна отримати з графіка g1(x)=|х-4| так: виконати паралельне перенесення графіка g1(x)вздовж осі Оуна |a| одиниць вниз; частину графіка, яка знаходиться під віссю Ох, симетрично відобразити відносно осі Ох.
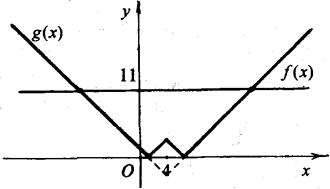
У цьому випадку рівняння має два розв’язки.
6. Якщо а=11, графіки функцій f(x) та g(х) перетинаються в трьох точках.
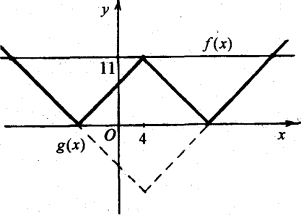
7. Якщо а>11, рівняння матиме чотири розв’язки, оскільки графіки f(x)і g(x) перетинаються в чотирьох точках.
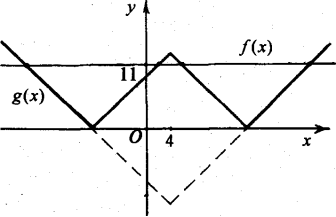
Як видно з наведених міркувань, рівняння має два розв’язки, коли -11<а<11 (випадки 1, 4 і 5). Тому а=10 – найбільше ціле значення параметра, яке задовольняє умову.
Відповідь. 10.
9). При якому значенні параметра т рівняння
|x2-2x-9|+m=0
має три розв’язки?
Розв’язання
Запишемо рівняння у вигляді:
|x2-2x-9|=-m
Рівняння має розв’язки, якщо т≤0. Шуканим значенням параметра т буде те, при якому графіки функцій
f(x)=|x2-2x-9| i g(x)=-m
перетинаються в трьох точках.
Графік функції f(x)=|хг-2х-9| отримаємо з відповідного графіка квадратичної функції, відобразивши частину графіка, яка знаходиться під віссю Ох, симетрично відносно цієї осі.
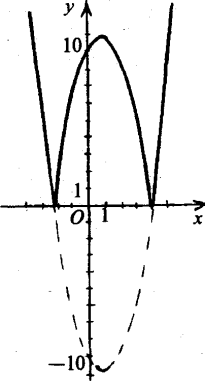
- Якщо т>0, графіки f(x) і g(x) не перетинаються, і рівняння не має розв’язків.
- Якщо т=0, графік функції g(x)=-т збігається з віссю Ох, і рівняння має два розв’язки.
- Якщо -10<т<0, графіки g(x)і f(x)перетинаються в чотирьох точках. Тому рівняння має чотири розв’язки.
- Якщо т=-10, графіки g(х) і f(x) мають три спільних точки, а рівняння – три розв’язки.
- Якщо т<-10, рівняння має два розв’язки.
Отже, рівняння має три розв’язки, якщо т=-10.
Відповідь. -10.
10). Для якого найбільшого значення параметра а, система
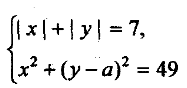
має єдиний розв’язок?
Розв’язання
х2+(у-а)2=49 – коло з центром у точці (0; а) і радіусом, який дорівнює 7.
| x | + | y | = 7 – ромб з вершинами в точках (7; 0), (0; 7), (-7; 0), (0; -7).
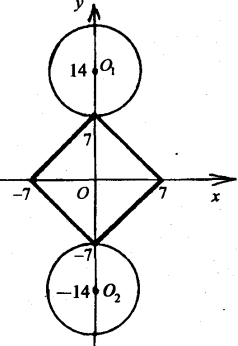
Система матиме єдиний розв’язок, коли коло і ромб перетинатимуться в одній точці. Така ситуація можлива, якщо центр кола знаходиться в одній із точок:
О1(14; 0) або О2(-14; 0).
Тому шукане значення параметра а=14.
Відповідь. 14.
Р о з д і л ІІ
Графіки функцій пов’язаних
із символами max і min
У цьому розділі показано, як, знаючи графіки функцій y1=f1(x), y2=f2(x),…,yn=fn(x) побудувати графіки функцій f(х)=тах(f1(х), f2(х),…fn(х)) та f(х)=mіn(f1(х), f2(х),…fn(х)) на спільній ОВ функцій fi(х).
Основним положенням є таке твердження: якщо на деякому проміжку графік функції f1, розташований не нижче (не вище) від графіка функції f2, то на цьому проміжку
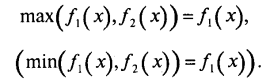
Приклад 1.
Побудувати графік функції у=max(х-2, -2).
Розв’язання
На рис. 1 показано графік функцій ух=х-2,у2=-2. Очевидно,
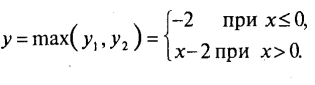
Шуканий графік показаний на рис. 2.
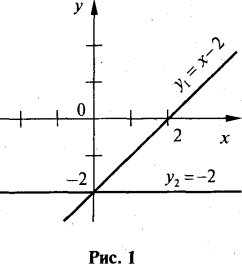
Приклад 2.
а) Побудувати графік функції
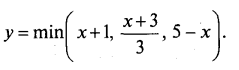
б) Довести нерівність у≤ 2.
в) Довести тотожність
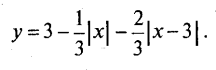
г) Скільки коренів має рівняння у=а, залежно від значення а?
д) Розв’язати рівняння у=а (залежно від значення а).
Розв’язання
а) Побудуємо графіки функцій
![]() ,
, ![]() ,
, ![]()
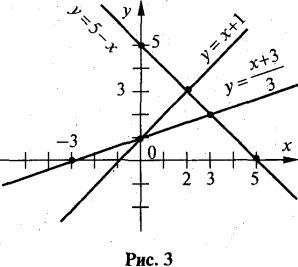
На рис. 3ми бачимо, що
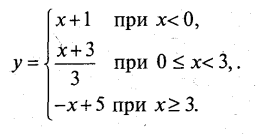
На рис. 4 показаний графік функції у.
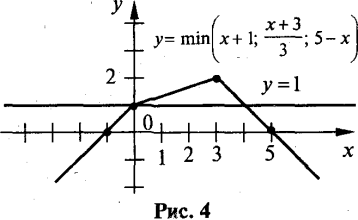
б) За рис. 4 визначаємо, що ![]() . Отже, у≤2.
. Отже, у≤2.
в) Побудуємо графік криво-лінійної функції
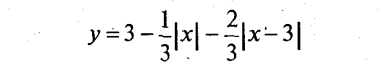
Графіки цієї і даної функції співпадають, отже, твердження в) справедливе.
г) Проводячи горизонталі з рівняннями у=а, встановлено, що рівняння має два корені при а<2, один корінь при а=2 і не має жодного кореня при а > 2.
д) При а≤ х+1=аабо 5-х=а, отже, при а≤1 х=a-1або х=5-а.
При ![]() або 5-х=а, отже, при 1<а≤2 х=3а-3або х=5-а.
або 5-х=а, отже, при 1<а≤2 х=3а-3або х=5-а.
При а>2 розв’язків немає.
Приклад 3.
а) Побудувати графікфункції
у = max(x +2,2-х-х2).
б) Проанкетуватифункцію.
в) Скільки коренів, залежно від а, має рівняння у=a?
г) Розв’язати рівняння у=а.
д) При яких значеннях параметра а рівняння у=а має рівно три корені?
Розв’язання
а) На рис. 5 показані графіки функцій у1=х+2 та у2=2-x-х2.
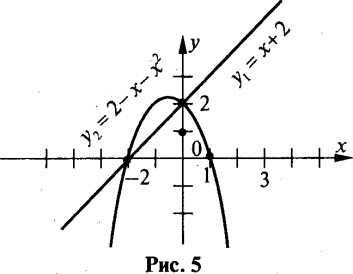
Очевидно,
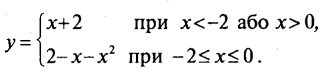
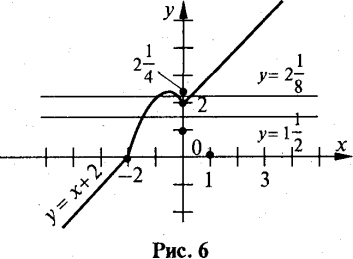
Шуканий графік показано на рис. 6.
б) D(y)=R;функція має єдиний корінь х=-2, функція додатна при х>-2, від’ємна при х< -2; функція зростає на кожномуз проміжків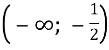 , (0;+∞); функція спадає напроміжку
, (0;+∞); функція спадає напроміжку 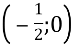 ; функціямає локальний максимуму точці
; функціямає локальний максимуму точці ![]()
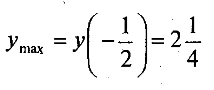
і локальний мінімум у точці x=0 . уmin =y(0)=2.
в) Проводячи горизонтальні прямі з рівняннями у=а, дістанемо, що рівняння у=а має один корінь при а<2 або а>2![]() , два корені при а=2 або а=2
, два корені при а=2 або а=2![]() , три корені при 2<а<2
, три корені при 2<а<2![]() .
.
г) При а≤0 х=a-2, при 0<а<2 ![]() абох=а-2, при а=2
абох=а-2, при а=2![]() х=-
х=-![]() або х=
або х=![]() а>2
а>2![]() .
.
д) Рівняння має рівно три кореніпри2<а<2![]() .
.
Приклад 4
Побудувати графік функції
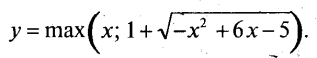
Розв’язання
Область визначення даної функції є множиною розв’язків нерівності
–x2+6x-5≥0, 1≤x≤5.
Отже, D(y)=[1; 5]. Розглянемо функцію

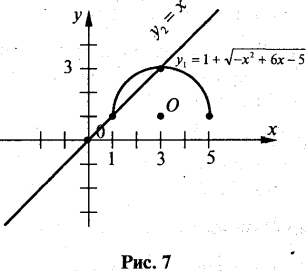
Графіком функції y1є півколо з центром (3, 1) і радіусом 2. На рис. 7 показані графіки функцій
![]()
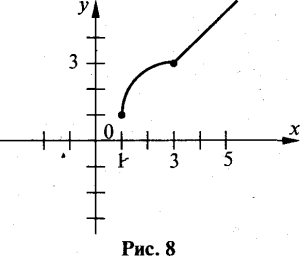
Шуканий графік показаний на рис. 8.
Приклад 5
Побудувати графік функції
![]()
Розв’язання
Очевидно,x2+x-3<x2+x-1 при ![]()
Приклад 6
а) Побудувати графік функції у=min(22, 2-х).
б)Довести тотожність
min(2х, 2-х)=2-|x|.
в)Скільки коренів має рівняння у=а, залежно від значення параметра а?
г) Розв’язати рівняння у=а.
д)При яких значеннях параметра а нерівність у≤а не має розв’язків?
е) При яких значеннях параметра а нерівність у≤а виконується при х ![]()
ж) Розв’язати нерівність у>а.
Розв’язання
а) На рис. 9 показані графіки функцій у1=2хтау2=2-x.
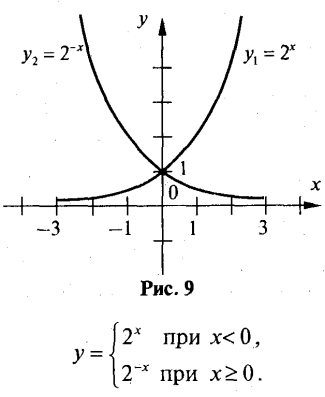
Шуканий графік показаний на рис. 10.
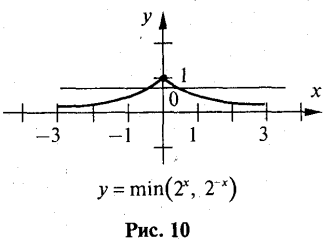
б) Помітимо, що

Отже, у =2-|x|.
в) Проводячи горизонтальні прямі з рівняннями у=а, бачимо, що при а≤0 або а>1коренів немає; при а=1 функція має єдиний корінь х=0; при 0<а<1 функція має два корені.
г) Маємо рівняння 2-|x|=a (дивись пункт б). При а<0 або при а>1 коренів немає, при а=1 х=0; при 0<а<1
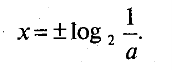
д) При а≤0 нерівність у≤а не має розв’язків.
е) При а>1 нерівність у≤а виконується при х![]()
ж) При а≥1 х ![]()
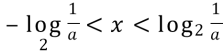 , при а≤0 х
, при а≤0 х![]()
Приклад 7.
Побудувати графік функціїy=min(sin x, cos x), 0≤х≤2![]()
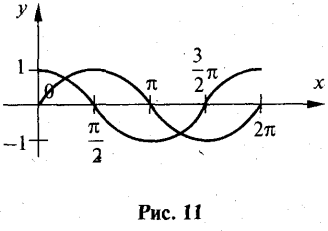
Розв’язання
На рис.11показані графіки функцій y1=sin x(0≤х≤2![]()
![]()
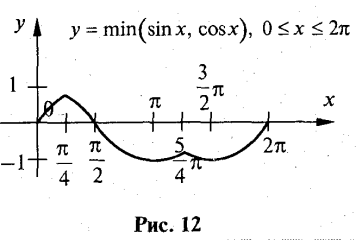
Шуканий графік показаний на рис. 12.
Приклад 8.
а) побудувати графік функції
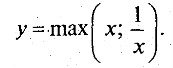
б) Проанкетувати цю функцію.
в) Розв’язати рівняння у = а.
г) Розв’язати нерівність у > а.
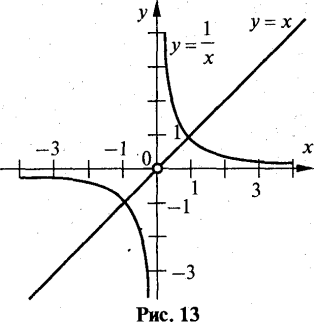
Розв’язання
На рис. 13 показані графіки функцій y1=х, у2= ![]() (на графіку функції у=х вилучено точку O(0; 0). Шуканий графік показаний на рис. 14
(на графіку функції у=х вилучено точку O(0; 0). Шуканий графік показаний на рис. 14
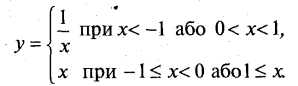
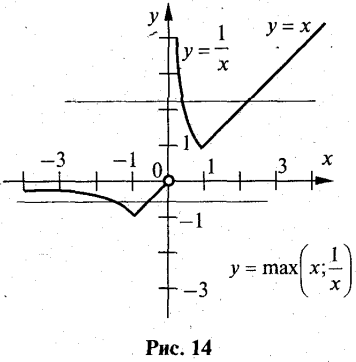
б) D=(_∞; 0) ![]()
Функція спадає на кожному з проміжків (-∞; -1) та (0 ; 1); зростає на кожному з проміжків (-1; 0) та(1; +∞).
![]()
Графік функції має горизонтальну асимптоту у = 0 (на -∞) та вертикальну асимптоту — вісь OY.
в)При а< -1 розв’язків немає, при а = -1 є один розв’язок х=-1, при -1<а<0 є два розв’язки х1=![]() , x2=а, при 0<а<1розв’язків немає, при а=1 є один розв’язок х=1, при а>1є дварозв’язки х3=
, x2=а, при 0<а<1розв’язків немає, при а=1 є один розв’язок х=1, при а>1є дварозв’язки х3=![]() , х4=а.
, х4=а.
г) При а<-1
![]()
Приа=-1
![]()
При-1<а< 0
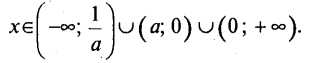
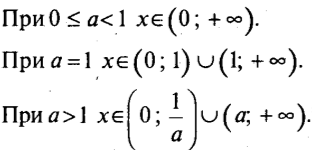
Приклад 9.
Яку найбільшу кількість коренів може мати рівняння
max(sin x; ln x)= а,
залежно від значень параметра a?
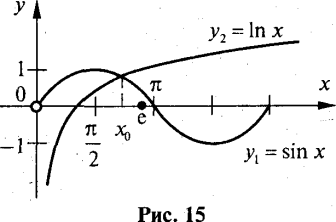
Розв’язання
На рис. 15 показані графіки функцій у1=sinx(без точки O(0; 0)) та у2=lnx.На проміжку![]() функція у1 спадає, а функція у2 зростає. Оскільки обидві функції неперервні, на проміжку
функція у1 спадає, а функція у2 зростає. Оскільки обидві функції неперервні, на проміжку![]() рівняння sinx=lnx має єдиний корінь х0. На рис. 16 показаний графік функціїу=max(sinх; lnx).
рівняння sinx=lnx має єдиний корінь х0. На рис. 16 показаний графік функціїу=max(sinх; lnx).
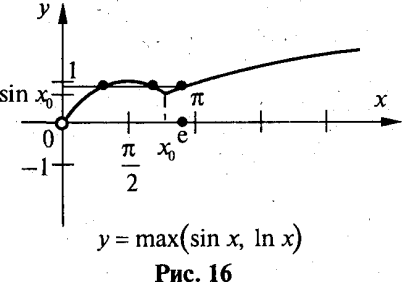
За графіком встановлюємо, що при а≤0 коренів немає; при a ![]()
![]()
![]()
Відповідь. Три.
Приклад 10
Побудуйте графік функції
![]()
Розв’язання
Помітимо, що
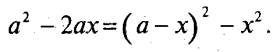
Враховуючи, що |а| ≤ 1, маємо три випадки.
1) |х| ≤ 1. (а-х)2-х2≥х2, причому рівність досягається лише при х=а. Отже, при |х|≤ 1 у = -х2.
2) х> 1. Тепер рівність х = а не досягається, бо х>а. Помітимо, що при х>1
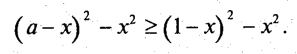
Дійсно,
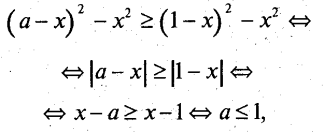
що справедливо. Отже, при х> 1
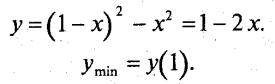
3) х<1. Міркуючи аналогічно пункту 2), дістанемо, що у=1+2х.утіп=у(-1).
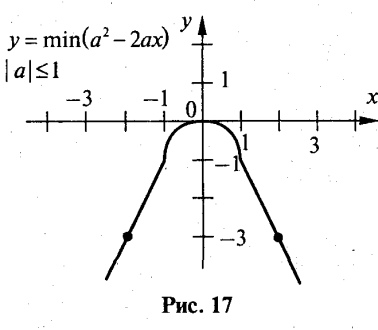
Таким чином, графік даної функції складається з трьох частин
Р о з д і л ІІІ
Задачі графічного змісту з теми:
«Тригонометричні функції»
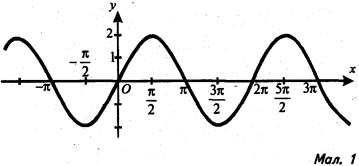
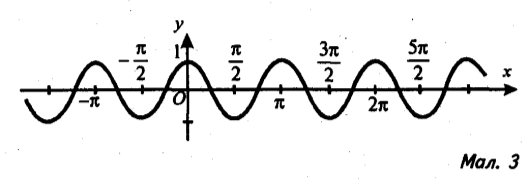
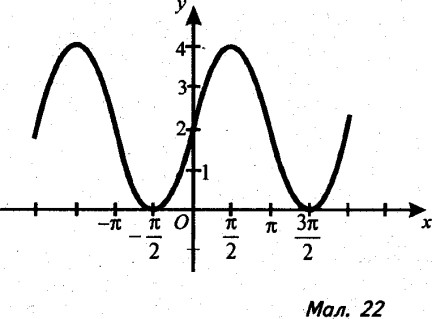
1). Визначте, графік якої тригонометричної функції зображено на малюнку 1.
2). Користуючись графіками функцій, зображеними на малюнках 2, 3, виконайте завдання.
а) Для яких значень х
f(x)=0; f(х)<0; f(x)>0?
б) Знайдіть проміжки зростання та спадання функції.
в) Вкажіть значення х, для яких функція має максимум або мінімум.
г) Чи має функція обернену на множині R?
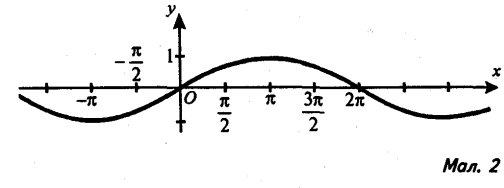
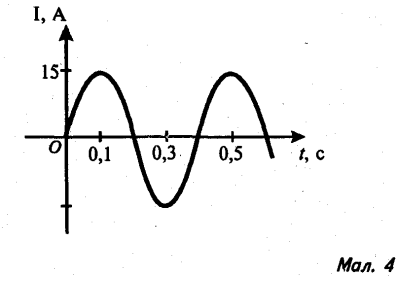
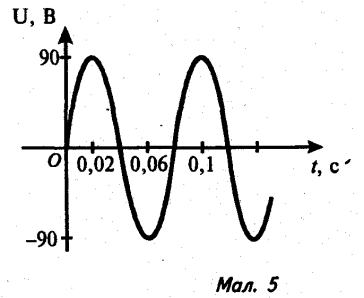
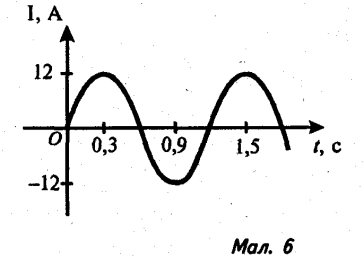
3). За графіками, які зображено на малюнках 4-7, знайдіть амплітуду сили струму (або напруги), період коливання. Запишіть закон залежності сили струму (або напруги) від часу.
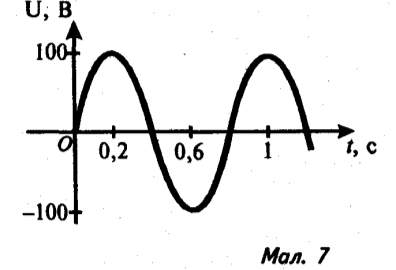
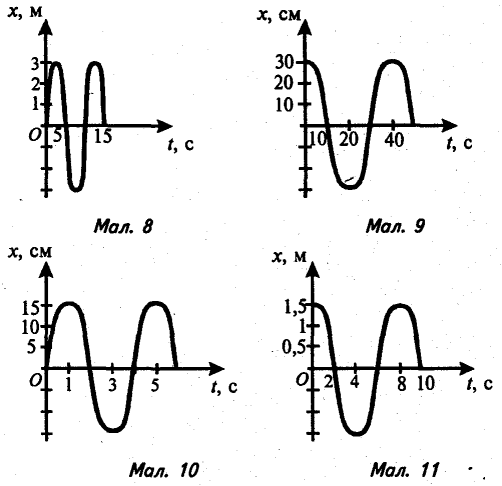
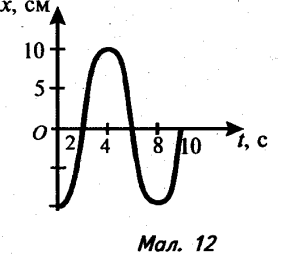
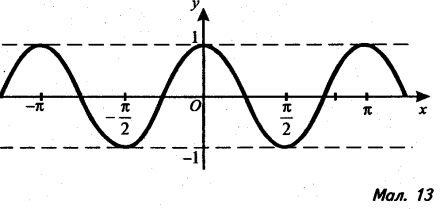
4). На малюнках 8-12 зображено графіки залежності координати х від часу tдля гармонічних коливань. Який графік відповідає коливанням з найбільшою амплітудою?
5). На малюнках 13, 14 зображено графіки одного з гармонічних коливань. Назвіть, якого.

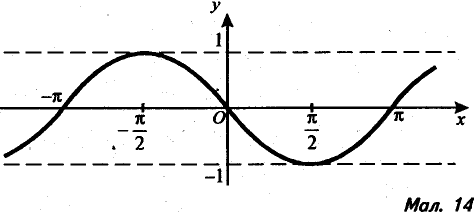

- Побудуйте графік функції у = 3sin2x. Знайдіть: її область визначення та множину значень; нулі функції; точки максимуму і мінімуму; найбільше і найменше значення; дослідіть її на парність, періодичність; назвіть проміжки сталого знака функції і проміжки монотонності. Чи має графік функції вісь симетрії, центр симетрії?
7). а) Скільки розв’язків має рівняння sinх = а на проміжку [0; 4![]()
б) Скільки розв’язків має рівняння cos x= а на проміжку [0; 4![]()
8). На малюнках 15-17 зображено графіки залежності напруги від часу:
а) на виході трансформатора;
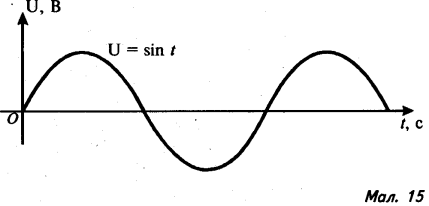
б) на виході однопівперіодноговипрямлювача;
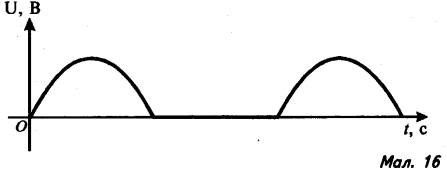
в) на виході двопівперіодноговипрямлювача.
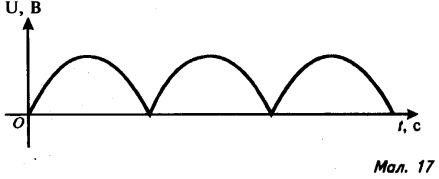
У випадках б) і в) задайте залежність напруги від часу аналітично.
9). Побудуйте графік функції:
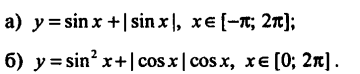
10). Точка рухається за законом:
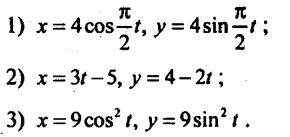
Знайдіть рівняння її траєкторії в координатній формі; покажіть на малюнку положення точки в початковий момент часу та напрям її руху.
11). Назвіть послідовність перетворень, за допомогою яких з графіка функції f(x) можна отримати графік функції ![]()
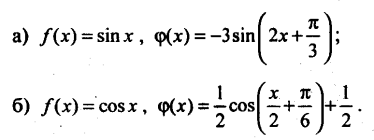
12). Побудуйте графік функції:
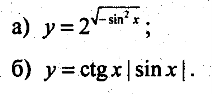
13). Складіть графічно два гармонічні однаково напрямлені коливання, у яких частоти відносяться як 1 : 2, а амплітуди відповідно як 2 : 1.
Знайдіть частоту складного коливання. Чи буде складне коливання:
а) гармонічним;
б) періодичним?
14). Складіть графічно два гармонічні однаково напрямлені коливання, у яких частоти відносяться як 1 : 3, а амплітуди відповідно як 2 : 1.
Знайдіть частоту складного коливання. Чи буде складне коливання:
а) гармонічним;
б) періодичним?
15). Два гармонічні однаково напрямлені коливання однакових періодів і амплітуд зміщені по фазі одне відносно другого на ![]() . Побудуйте графік складного коливання. Чи буде складне коливання гармонічним? Знайдіть період складного коливання. Яка різниця фаз між складним коливанням і його складовими коливаннями?
. Побудуйте графік складного коливання. Чи буде складне коливання гармонічним? Знайдіть період складного коливання. Яка різниця фаз між складним коливанням і його складовими коливаннями?
16). Два гармонічні однаково напрямлені коливання однакових періодів і амплітуд зміщені по фазі одне відносно другого на ![]()
17). а) Користуючись діаграмою утворення поперечної хвилі (мал. 18), з’ясуйте, скільком хвилям відповідає кожна з чотирьох частин цієї діаграми.
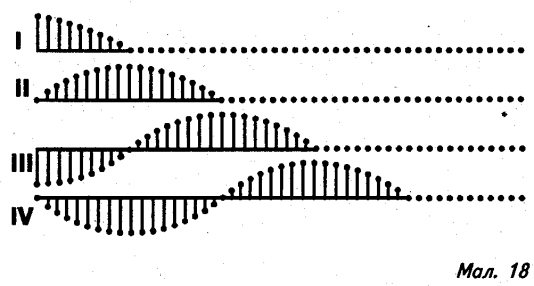
б) Визначте частоту коливань, якщо на малюнку до попередньої задачі (частина IV) зображено зменшену в 10 раз довжину звукової хвилі в залізі. Швидкість поширення звуку в залізі v = 5000 м/с.
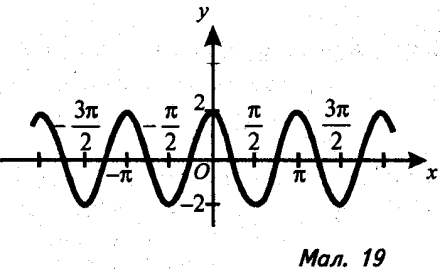
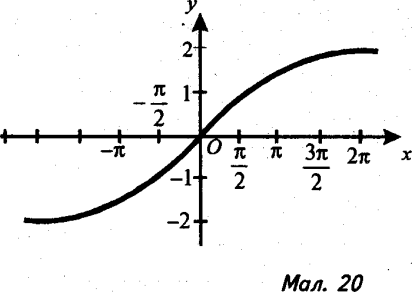
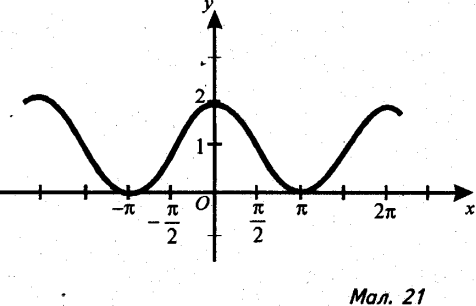
18). Серед графіків, які зображено на малюнках 19-22, назвіть графік функції:
а) у = 2sin x + 2 ;
б) у = 2cos2x; .
в) ![]() ;
;
г) y=cos2x+1.
19). Джерело енергії має напругу несинусоїдальної форми
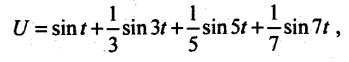
де U — напруга, В; t — час, с.
Побудуйте графік напруги джерела.
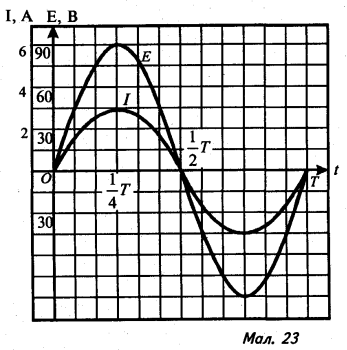
20). На малюнку 23 зображено графіки зміни ЕРС й сили змінного струму в колі тільки з омічним опором. Побудуйте графік потужності змінного струму. У скільки разів частота коливань потужності більша від частоти змінної ЕРС?
Примітка. Р = ЕІ, де Р - потужність змінного струму, Е - змінна ЕРС, I – змінна сила струму.
21). Кулька обертається по спіралі від точки А до точки В зі сталою кутовою швидкістю (мал. 24).
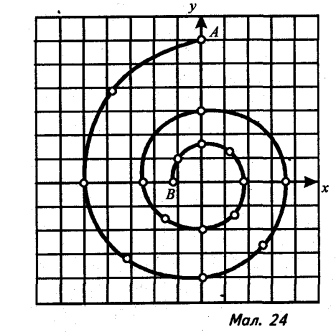
а) Побудуйте графік руху проекції кульки на вісь ординат.
б) Знайдіть кількість повних коливань проекції кульки.
в) Побудуйте криву, що показує, як змінюється амплітуда коливань у часі.
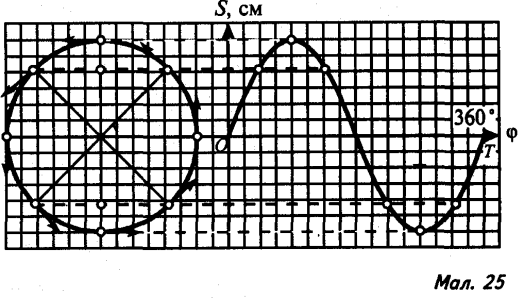
22). Кулька рівномірно обертається по колу з радіусом r = 3 см. На малюнку 25 зображено графік коливання проекції на вертикальний діаметр цього кола.
Побудуйте графік коливання проекції на горизонтальний діаметр цього кола. Порівняйте цей графік з даним.
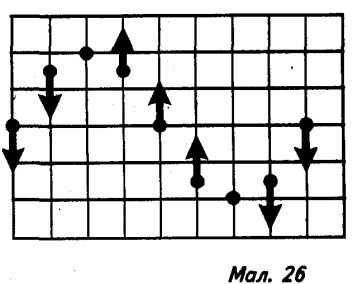
23). На малюнку 26 показано розміщення частинок середовища та напрям їх руху в поперечній хвилі. Накресліть положення частинок середовища танапрям їх руху через ![]() ,
, ![]() ,
, ![]() і T,деТ— періодколивання.
і T,деТ— періодколивання.
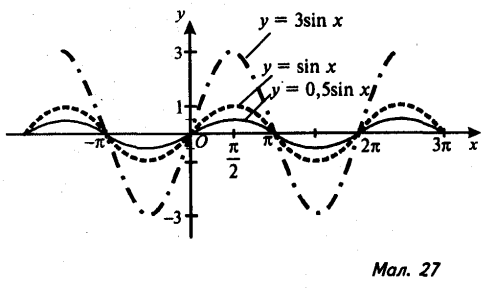
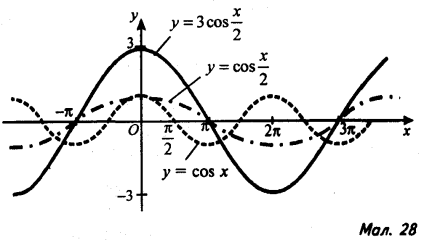
24). Проаналізуйте малюнки 27-29; назвіть геометричні перетворення, які виконуються для побудови графіків функцій; зробіть загальні висновки.
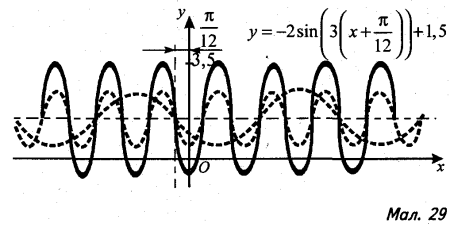
25). Побудуйте графік функції:
- y = tg x ctg x;
- у= sec x |cos x|;
- y = 2sin x |cos x|;
- у=|sin x| + sin x .
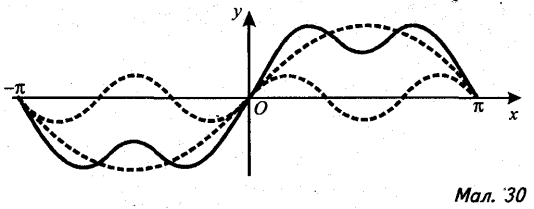
26). На мал. 30 зображено графіки функцій у = sin xі![]() (пунктирні лінії). Як можна задати аналітично функцію, графік якої зображено суцільною лінією?
(пунктирні лінії). Як можна задати аналітично функцію, графік якої зображено суцільною лінією?
В И С Н О В К И
Математика є тим предметом, який забезпечує вивчення на сучасному рівні ряду шкільних предметів, як точних, так і гуманітарних. Крім того математика є часто профілюючим предметом при вступі у вузи. Тому важливо навчити учнів швидко і правильно розв’язувати вправи графічного змісту.
Враховуючи те, що в учнів виникають певні труднощі під час розв’язування вправ графічного змісту, дана робота допоможе знайти найбільш раціональні способи їх розв’язування, що дає змогу економити час, а учням краще усвідомити та осмислити навчальний матеріал.
С П И С О К В И К О Р И С Т А Н И Х Д Ж Е Р Е Л
- Параскевич С. Задачі графічного змісту як модель проблемної ситуації: Математика в школі. – 2005.-№5.
- Параскевич С. Задачі графічного змісту при вивчені алгебри і початків аналізу в технікумі: Навчально-методичний посібник. Херсон: Видавництво ХДД, 2004.
- Слєпкань З.І. Методика навчання математики. – К.: Зодіак – ЕКО, 2000.
- О.М. Вероний, Р.П. Куцова. Задачі з параметрами: Ж. Математика. – 2001. – №4.
- В.С.Зубаха. Розв’язування вправ з модулями. Ж.Математика –2001.– №4.
- Наталія Крикун. Задачі графічного змісту. Ж. Математика – 2008. – №33.
- Р.П. Ушаков. Графіки функцій, пов’язаних із символами maximin. Ж.Математика – 2006. – №1.
1


про публікацію авторської розробки
Додати розробку
