Методичні вказівки щодо виконання практичної роботи «Дослідження оптимального коду Хаффмана»
Новокаховський приладобудівний фаховий коледж
Лабораторія № 607
Дисципліна: «Основи кодування та передавання інформації»
МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ВИКОНАННЯ ПРАКТИЧНОЇ РОБОТИ
«Дослідження оптимального коду Хаффмана»
Мета роботи: вивчити властивості оптимального кодування методом Хаффмана, принципи його побудови; виконати розрахунок параметрів ефективності оптимального коду Хаффмана.
Теоретичні відомості
Код Хаффмана є оптимальним префіксним кодом для дискретних джерел за критерієм: мінімальна середня довжина кодової комбінації знака (мінімальна надмірність).
Алгоритм Хаффмана більш практичний і по ступені стиску не уступає методу Шеннона-Фано, більше того, він стискає максимально щільно.
Код Хаффмана відіграє важливу роль у кодуванні зображень. Він є основною частиною алгоритму кодування за стандартами JPEG, MPEG. Код Хаффмана є стандартним для кодування факсимільних повідомлень, а також він використовуються для кодування аудіосигналів.
Алгоритм побудови коду Хаффмана базується на кодовому дереві і має таку послідовність процедур:
1. Упорядкування знаків шляхом розміщення їх у порядку спадання їхніх ймовірностей.
2. Вибирають два вузли з найменшими ймовірностями. З них будують дві гілки, які сходяться в один вузол, що відповідає складеному знаку, а його ймовірність дорівнює сумі ймовірностей вузлів, з яких вийшли гілки. Гілкам приписують символи 1 і 0, наприклад, верхній вітці 1, а нижній вітці 0.
3. Повторення кроків 1 і 2 – доки не буде досягнуто кореня кодового дерева.
4. Кодова комбінація знаку формується шляхом виписування символів, починаючи з кореня кодового дерева, проходячи по вітках до цього знаку.
Приклад 1. Задано джерело дискретних повідомлень з МА = 8. Знаки джерела незалежні і мають такі ймовірності: P(a1) = 0,1; P(a2) = 0,5; P(a3) = 0,2; P(a4) = 0,01; P(a5) = 0,09; P(a6) = P(a7) = 0,015; P(a8) = 0,07.
Побудувати код Хаффмана. Обчислити ентропію джерела, середню довжину кодових комбінацій, коефіцієнт ефективності та коефіцієнт стиснення отриманого коду, порівняти коефіцієнти надмірності на вході та виході кодера.
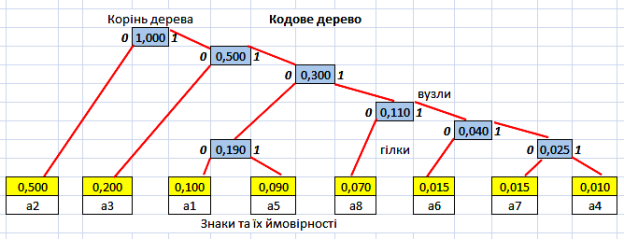
Розв’язання. Побудову коду Хаффмана наочно показано на рисунку 1.
Символи попарно об'єднуються у нові символи, починаючи з тих, що мають найменшу йомовірність, а потім, з урахуванням ймовірностей утворених символів, знову проводять попарне об'єднання символів з найменшими ймовірностями, і таким чином, будують двійкове кодове дерево, у вершині якого стоїть символ з ймовірністю 1.
Кодова таблиця
|
Знаки, ak |
Ймовірність знаків, P(ak) |
Кодова комбінація |
|
а2 |
0,50 |
0 |
|
а3 |
0,20 |
10 |
|
а1 |
0,10 |
1100 |
|
а5 |
0,09 |
1101 |
|
а8 |
0,07 |
1110 |
|
а6 |
0,015 |
11110 |
|
а7 |
0,015 |
111110 |
|
а4 |
0,01 |
111111 |
Рисунок 1 – Приклад побудови кодового дерева
Середня довжина кодових комбінацій:
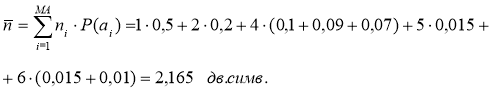
Ентропія джерела повідомлення А:
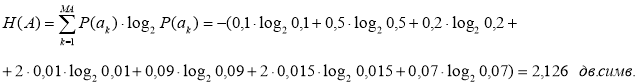
Порівняємо надмірність повідомлень на вході та на виході кодера (див. рисунок 2).
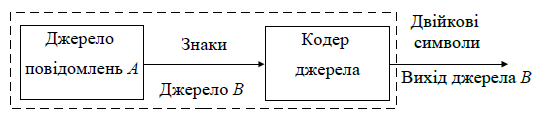
Рисунок 2 – Кодування джерела повідомлень
Коефіцієнт надмірності джерела А дорівнює:
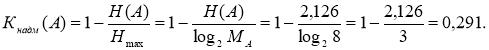
Для розрахунку коефіцієнта надмірності джерела В (по виходу кодера) необхідно обчислити ентропію цього джерела H(В). Для цього знайдемо йомовірності символів 1 і 0 на виході джерела В.
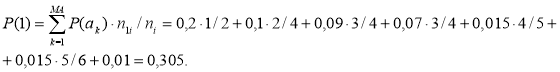
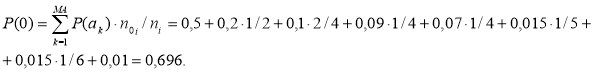
Ентропія джерела В складе:
H(B) = -[P(1)·log2P(1) + P(0)·log2P(0)] =
-[0,305·log2 0,305 + 0,696·log2 0,696] = 0,887 дв.од.
Коефіцієнт надмірності джерела В складе:
Кнадм(В) = 1- Н(В) = 1 – 0,887 = 0,013.
Отже, Кнадм(В) < Кнадм(A ), тобто ефективне кодування зменшує надмірність.
Для порівняння отриманого коду з іншими кодами розрахуємо:
a) коефіцієнт ефективності коду:
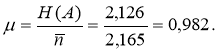
б) коефіцієнт стиснення нерівномірного коду:
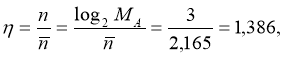
де n – довжина рівномірного коду, яка визначається як ціле число, що задовольняє умові:
n ≥ log2MA.
З прикладe 1 випливає, що коефіцієнт стиснення ефективного кодів не э надто значний. Це тому, що обсяг алфавіту джерела невеликий. Для джерел з більшим числом знаків і більшою різноманітністю ймовірностей цей показник підвищується.
Звичайно параметри коду Хаффмана дещо кращі, ніж параметри коду Шеннона-Фано для одного і того ж джерела. Це пояснюється тим, що алгоритм побудови коду Хаффмана дає можливість повторного упорядкування знаків у порядку убування їхніх ймовірностей і вибору пар знаків з близькими ймовірностями (п. 2 алгоритму). Тому вважають, що код Хаффмана - оптимальний, а код Шеннона-Фано не завжди є оптимальний.
Порядок виконання роботи
Побудуйте оптимальний код Хаффмана для передавання повідомлень.
Ймовірності появи літер первинного алфавіту А занесені в таблицю 1:
Таблиця 1
|
Варіант |
Ймовірності появи літер первинного алфавіту |
|
1 |
p(Ai) = {0,38; 020; 0,14; 0,09; 0,07; 0,045; 0,035; 0,025} |
|
2 |
p(Ai) = {0,54; 020; 0,09; 0,06; 0,05; 0,03; 0,02; 0,01} |
|
3 |
p(Ai) = {0,45; 023; 0,18; 0,07; 0,04; 0,03; 0,02; 0,01} |
|
4 |
p(Ai) = {0,35; 026; 0,17; 0,07; 0,05; 0,04; 0,035; 0,025} |
|
5 |
p(Ai) = {0,37; 027; 0,16; 0,065; 0,05; 0,04; 0,03; 0,015} |
|
6 |
p(Ai) = {0,41; 025; 0,135; 0,075; 0,055; 0,035; 0,022; 0,018} |
|
7 |
p(Ai) = {0,40; 024; 0,155; 0,06; 0,048; 0,04; 0,036; 0,021} |
|
8 |
p(Ai) = {0,39; 023; 0,165; 0,078; 0,046; 0,038; 0,031; 0,022} |
Обчисліть ентропію джерела, середню довжину кодових комбінацій, коефіцієнт ефективності та коефіцієнт стиснення отриманого коду, порівняйте коефіцієнти надмірності на вході та виході кодера.
Результати побудови коду Хаффмана занесіть в таблиці 2, 3, 4.
|
Таблиця 2 |
|
|
|
|
|
|
|
|
|
||||||||
|
Знак |
P(ai) |
Код |
ni |
ni |
Н(A) |
кільк.1 |
кільк.0 |
P(1) |
P(0) |
||||||||
|
a1 |
|
|
|
|
|
|
|
|
|
||||||||
|
a2 |
|
|
|
|
|
|
|
|
|
||||||||
|
а3 |
|
|
|
|
|
|
|
|
|
||||||||
|
а4 |
|
|
|
|
|
|
|
|
|
||||||||
|
а5 |
|
|
|
|
|
|
|
|
|
||||||||
|
a6 |
|
|
|
|
|
|
|
|
|
||||||||
|
a7 |
|
|
|
|
|
|
|
|
|
||||||||
|
а8 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таблиця 3
|
Середня кількість двійкових знаків на літеру коду А, n |
Ентропія джерела повідомлень А, H(А) |
Максимальна ентропія джерела повідомлень, Hmax |
Коефіцієнт стиснення, η |
Коефіцієнт ефективності коду, μ |
|
|
|
|
|
|
Таблиця 4
|
Коефіцієнт надмірності джерела повідомлень А |
Ймовірність символів „1“ на виході джерела В
|
Ймовірність символів „0“ на виході джерела В
|
Ентропія джерела В H(В) |
Коефіцієнт надмірності джерела повідомлень В |
|
|
|
|
|
|
Зміст звіту роботи
- Назва та ціль роботи.
- Кодове дерево.
- Формули розрахунків.
- Таблиці результатів розрахунків.
- Короткі висновки з роботи.
- Відповіді на контрольні питання.
Контрольні питання
- Причини надмірності повідомлень?
- Що називається оптимальним кодуванням?
Література
- Беркман Л.Н., Бондарчук А.П., Гайдур Г.І., Чумак Н.С. Кодування джерел інформації та каналів зв’язку : навчальний посібник. – Київ: ННІТІ ДУТ, 2018.
- Фетюхіна Л. В. Теорія інформації та кодування : навч.-метод. посібник/ Л. В.Фетюхіна, О. А. Бутова – Харків: НТУ «ХПІ», 2012.
© НКПФК, Тосенко О.М., 2023
1


про публікацію авторської розробки
Додати розробку
