Методичний посібник "Формування вмінь математичного моделювання в учнів основної школи у процесі навчання геометрії"

Департамент освіти і науки

Полтавської обласної державної адміністрації

Відділ освіти Пирятинської міської ради Полтавської області

Пирятинський ліцей Пирятинської міської ради

Полтавської області

 

 

 

 

М.О.Філімонова

 

Формування вмінь

математичного моделювання

в учнів основної школи у процесі навчання геометрії

 

 

 

 

 

Пирятин – 2017

      Департамент освіти і науки

Полтавської обласної державної адміністрації

Відділ освіти Пирятинської міської ради Полтавської області

Пирятинський ліцей Пирятинської міської ради

Полтавської області

 

 

 

 

М.О.Філімонова

 

 

 

 

 

Формування вмінь

математичного моделювання

в учнів основної школи у процесі навчання геометрії

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пирятин – 2017

       Філімонова Марія Олександрівна,

       учитель математики Пирятинського ліцею

       Пирятинської міської ради Полтавської області,

       стаж за фахом – 9 років,

       спеціаліст першої  категорії

 

 

 

 

 

 

 

 

Математичне моделювання, виступаючи потужним методом пізнавальної діяльності, сприяє формуванню в учнів основних прийомів розумової діяльності та комунікативних навичок; вміння моделювати ситуацію або процес, аналізувати і порівнювати дані, інтерпретувати результати, оптимізувати, оцінювати з різною точністю; викликає стійкий інтерес до математики; допомагає в здійсненні пропедевтичної профорієнтаційної роботи.

Розроблена методика формування в учнів основної школи вмінь математичного моделювання у процесі навчання геометрії може бути використана вчителями основної школи, методистами інститутів післядипломної освіти, авторами шкільних підручників, методичних посібників для вчителів.

Рецензенти:

Саполович О.В. – завідуюча кафедрою математики, фізики та інформатики Пирятинського ліцею Пирятинської міської ради Полтавської області

Сав’яненко М.О.– керівник міського методичного об’єднання вчителів математики

Схвалено науково-методичною радою Пирятинського ліцею Пирятинської міської ради Полтавської області (протокол № 3 від 24.01.2017),

рішенням атестаційної комісії відділу освіти Пирятинської міської ради Полтавської області (протокол № 4 від 14.03.2017).

Зміст

 

Вступ ………………………………………………………………………………..4

Методика формування в учнів основної школи вмінь математичного моделювання у процесі навчання геометрії……………………………..............7

1. Пропедевтичний етап вивчення математичного моделювання……............7
2. Початковий етап вивчення математичного моделювання………………..12
3. Основний етап вивчення математичного моделювання…………………..26

Висновки……………………………………………………………………………36

Список використаних джерел……………………………………………………..40

Додатки……………………………………………………………………………...42

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

Місце освіти в суспільному житті України було, є і буде об’єктом досить запеклих дискусій, адже навіть пересічний громадянин держави поступово починає усвідомлювати, що освіта є джерелом добробуту для нього, а надто – для його дітей.

Нині стало очевидним, що “технологія майбутнього вимагає не мільйонів поверхово підготовлених людей, готових виконувати одноманітну роботу…а людей, які матимуть критичне мислення, які зможуть знаходити свій шлях у новому оточенні, які досить швидко встановлюватимуть нові стосунки в реальності, що постійно змінюється. Вона вимагає людей, у яких “майбутнє в крові”. Тому одне із першочергових завдань шкільної математичної освіти полягає в опануванні учнями такою системою математичних знань, умінь і навичок, яка б виявилася корисною у повсякденному житті та достатньою для формування наукового світогляду школярів,  їх інтелектуального розвитку та готовності до вибору майбутньої професії. Зробити це можна різними способами, один з яких – активізація пізнавального інтересу до вивчення математики шляхом формування в учнів знань, умінь і навичок математичного моделювання.

  Отже, пошук нових можливостей підсилення прикладної спрямованості шкільного курсу математики, засобів формування навичок математичного моделювання є перспективним напрямком досліджень в області теорії й методики навчання математики.

Механізми дослідження методів математичного моделювання та їх використання в різних галузях науки і техніки знайшли відображення у працях В.М.Глушкова, Б.В.Гнеденка, А.М.Колмогорова, Г.М.Морозова, А.М. Тихонова та інших дослідників. Аспекти дослідження математичних моделей засобами інформаційно-комунікаційних технологій, зокрема методичне забезпечення та методика навчання, розроблені М.І.Жалдаком, Є.І.Машбицем,  Г.О. Михаліним, Н.В.Морзе, С.А.Раковим та іншими методистами-науковцями. Методична система формування знань і вмінь математичного моделювання в процесі математичної та методичної підготовки вчителів математики в умовах особистісно-орієнтованого навчання висвітлена у дисертаційному дослідженні Л.Л. Панченко.

Дієвим заходом реалізації математичного моделювання на практиці є розв’язування прикладних задач. Основні положення прикладної спрямованості шкільного курсу математики розкрито у роботах Г.П. Бевза, Г.М.Возняка,  Ю.М.Колягіна, В.В.Фірсова та інших науковців. Розробкою сучасних технологій розв’язання проблеми прикладної спрямованості шкільного курсу математики займаються С.М. Лук’янова, Л.С. Межейнікова, А.В. Прус, Л.О.Соколенко, В.О.Швець та інші математики-методисти. Зокрема, у їхньому доробку не тільки наукові, а й практично значущі результати дослідження проблеми прикладної спрямованості шкільних курсів алгебри і початків аналізу, стереометрії, інтегрованого шкільного курсу “Математика”.

Проте, як засвідчив аналіз робіт, ще не всі аспекти проблеми формування й розвитку навичок математичного моделювання в учнів виявилися висвітленими. Питання прикладної спрямованості шкільного курсу геометрії основної школи до сьогодні залишається відкритим. Незважаючи на постійне реформування освіти, впровадження інноваційних технологій, вдосконалення підручників, методичних посібників, аналіз масової практики навчання дає змогу виділити в навчально-виховному процесі такі суперечності:

• між соціальним запитом щодо формування у школярів у процесі навчання математики загальнопредметних компетентностей, до яких належить і уміння використовувати методи математичного моделювання, та недостатнім рівнем сформованості таких умінь в учнів основної школи;
• між вимогами суспільства щодо особистісного спрямування навчально-виховного процесу, між потребами та інтересами учня і традиційними методами, формами й засобами навчання математики та геометрії;
• між наявним станом теоретичної розробки проблеми формування вмінь математичного моделювання та практикою навчання учнів основної школи;
• між необхідністю оволодіння учнями основної школи загальним умінням застосовувати отримані на уроках математики та геометрії знання у повсякденному житті та відсутністю у методичній науці відповідної системи, яка б передбачала формування цих умінь.

Таким чином, підвищена актуальність, теоретична і практична значущість визначеної проблеми та необхідність розв’язання виявлених суперечностей зумовили вибір теми методичного дослідження “Формування вмінь математичного моделювання в учнів основної школи у процесі навчання геометрії”.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИКА ФОРМУВАННЯ В УЧНІВ ОСНОВНОЇ ШКОЛИ УМІНЬ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ У ПРОЦЕСІ НАВЧАННЯ ГЕОМЕТРІЇ

Для набуття учнями відповідного рівня вмінь застосовувати методи математичного моделювання його навчання має бути наскрізним. Ми пропонуємо організувати процес формування вмінь математичного моделювання в кілька етапів:

1) пропедевтичний етап (5 – 6 класи), який передбачає формування уявлень про математичну модель, її види, деякі властивості; уміння будувати математичну модель до задачі або складати задачу за даною математичною моделлю;

2) початковий етап (7 – 8 класи), який передбачає формування поняття про математичну модель, її види, етапи математичного моделювання; уміння будувати або добирати доцільні математичні моделі до задачі;

3) основний етап (9 клас), який передбачає узагальнення знань про математичну модель, її види, етапи математичного моделювання; формування вміння використовувати інформаційно-комунікаційні технології при створенні та дослідженні математичної моделі;

4) дослідницький етап, який передбачає глибше вивчення математичного моделювання на гуртках, факультативах; написання наукових робіт в системі діяльності Малої академії наук (надалі МАН).

 

Пропедевтичний етап вивчення математичного моделювання

Шкільна геометрична освіта передбачає пропедевтику систематичного курсу геометрії в процесі навчання математики у 5–6 класах. Саме у цей період в учнів формуються уявлення про основні геометричні фігури та їх властивості, уміння виконувати найпростіші вимірювання і побудови, розв'язувати задачі на обчислення значень геометричних величин (довжин відрізків, градусних мір кутів, площ фігур, об'ємів тіл). Тому понятійний апарат, графічні уміння і навички, сформовані на цьому ступені вивчення курсу, мають стати міцним підґрунтям систематичного вивчення геометрії в наступних класах. Таким чином, матеріал, призначений для вивчення у 5–6 класах, уможливлює з одного боку поглиблення і розширення уявлень учнів про відомі їм геометричні фігури, а з іншого – є основою для систематичного вивчення геометрії в            7–9 класах.

Школярі 5–6 класів у процесі вивчення математики знайомляться з різними видами моделей, починаючи від знако-символьних (числовий і буквенний вираз, рівняння) і закінчуючи образними (схеми, таблиці, малюнки, рисунки геометричних фігур та тіл, діаграми).

Формування уявлення про числовий вираз як математичну модель відбувається в процесі складання до прикладної задачі виразу, результат обчислення якого задовольняє вимогу задачі. Наприклад:

Задача 1. З двох пунктів одночасно назустріч один одному виїхали два мотоциклісти. Швидкість одного з них дорівнює 56 км/год, а другого –              на 13 км/год більша. Знайди відстань між пунктами, якщо через 4 год відстань між мотоциклістами була 15 км.

Звичайно, слід скласти графічний запис задачі. 

Потім, проаналізувавши її умову і вимоги, скласти план розв’язання:

1. Знайти шлях, який подолав перший мотоцикліст.
2. Знайти швидкість другого мотоцикліста.
3. Знайти шлях, який подолав другий мотоцикліст.
4. Знайти загальну відстань між пунктами, додавши відстані, які подолали два мотоциклісти, і 15 км.

Далі згідно вищевказаного плану розв’язати задачу.

1.  56·4 – шлях, подоланий першим мотоциклістом.
2. 56+13 – швидкість другого мотоцикліста.
3. (56+13)·4 – шлях, подоланий другим мотоциклістом.
4. 56·4+(56+13)·4+15 – відстань між пунктами.

Варто наголосити учням, що складений числовий вираз 56·4+(56+13)·4+15 є знако-символьною моделлю задачі, а побудований на початку її графічний запис - образною. Обчисливши значення виразу, можна знайти, що відстань між пунктами дорівнює 515 км.

Подібне розв’язування задач не лише формує у школярів уявлення про модель та її види, а одночасно є пропедевтикою застосування в майбутньому алгебраїчного способу і значно спрощує роботу вчителя у цьому напрямку.

Методика вивчення теми “Числові і буквенні вирази. Рівняння” у контексті математичного моделювання, на мою думку, має складатися з двох етапів:

1. Формування уявлення про буквенний вираз як знако-символьну модель.
2. Формування уявлення про рівняння як знако-символьну модель.

На першому етапі важливо сформувати в учнів уміння складати буквенні вирази за умовою задачі та знаходити компоненти дій за результатом та іншими компонентами. Причому варто наголосити, що арифметична дія та її результат можуть мати тотожне знакове вираження. Також слід звернути увагу на те, що буквенний вираз, зокрема формула, дозволяє узагальнити розв’язання різних типів задач і скласти певні правила-орієнтири.

Зазначена вище робота дозволяє спростити процес навчання учнів розв’язуванню прикладних задач за допомогою рівнянь. Наприклад:

Задача 2. У трьох ящиках було 70 кг яблук. У другому ящику – вдвічі більше, ніж у першому, а в третьому – на 5 кг менше, ніж у другому. Скільки кілограмів яблук було у кожному ящику?

Слід скласти до задачі образну модель – схему.

1 ящик     ?

2 ящик                  у 2 рази більше

3 ящик                                                        на 5 кг менше

Хід розв’язання задачі може бути таким:

1. Позначимо за х – кількість яблук у першому ящику.
2. Тоді у другому ящику буде 2х яблук, а у третьому (2х–5) яблук.
3. За умовою задачі у всіх ящиках разом було 70 кг яблук, тому:

 

 

 

Маємо х+2х+(2х–5) = 70 – знако-символьну модель задачі.

4. Розв’язавши рівняння, отримаємо, що х = 15.
5. Тоді 2х = 2·15 = 30; 2х–5 = 2·15–5 = 25.
6. Отже, у першому ящику було 15 кг яблук, у другому – 30 кг, а у третьому – 25 кг. Здійснимо перевірку 15+30+25 = 70, 30:2 = 15, 25+5 = 30, що відповідає умові задачі.

На основі розв’язання подібних задач учитель має запропонувати учням пам’ятку (правило-орієнтир) для застосування алгебраїчного способу.

Також, враховуючи психолого-педагогічні особливості учнів 5–6 класів, при розв’язуванні прикладних задач за допомогою рівнянь, слід використовувати комп’ютерні презентації, оскільки наочне представлення умови задачі допомагає навіть найслабшим школярам правильно здійснити побудову математичної моделі.

Що стосується геометричного матеріалу, то процес його викладання має специфічні риси:

1. Зміст курсу і методи його викладання мають опиратися на життєвий досвід і попередні знання школярів, причому основою курсу повинно бути максимальне використання наочності (моделі геометричних об’єктів, комп’ютерні презентації тощо). Тому при вивченні тієї чи іншої геометричної фігури пропоную учням знайти у класі і поза ним предмети, моделями яких вона може бути, вказати випадки у повсякденному житті, коли необхідно побудувати, наприклад, прямі (у процесі побудови будівель, доріг, насадженні дерев і т.д.), знайти периметр прямокутника (при визначенні довжини огорожі, розмірів пришкільної ділянки, футбольного поля і т.д.) тощо.

2. Значну увагу приділяю формуванню усного і писемного мовлення учнів, їх грамотності.

3. Знайомство з новими поняттями, властивостями геометричних об’єктів має відбуватися під час проведення практичних робіт з елементами конструювання та вимірювальних робіт на місцевості. Адже вимірювальні роботи дають учням можливість ознайомитися з будовою і способами використання найпростіших землемірних приладів, із методами розв’язування певних практичних задач, унаочнюють деякі геометричні поняття, властивості фігур тощо, є ілюстрацією застосування методу математичного моделювання.

4. Система вправ має бути спрямована з одного боку на розвиток просторової уяви та абстрактного мислення, а з іншого – сприяти формуванню навичок виконання найпростіших логічних операцій.

5. Система вправ має включати значну частку прикладних задач, завдань на розвиток уміння бачити в навколишній дійсності геометричні фігури, здійснювати вимірювання “на око”.

Дотримання вищезазначених вимог забезпечить цілісність і неперервність вивчення систематичного курсу геометрії в основній та старшій школах.

Слід звернути увагу і на той факт, що великі труднощі у школярів при розв’язуванні прикладних задач, викликає процес заміни об’єктів, які описані в умові задачі, геометричними фігурами і термінами, оскільки для цього має бути гарно розвинене абстрактне мислення, що для 10–11-річних підлітків не є характерним.

Тому на початкових етапах необхідно робити акцент на завданнях, в яких поряд з вихідним об’єктом зазначається його математичний еквівалент. Наприклад:

Задача 3. Щоб зробити льох, викопали яму у вигляді прямокутного паралелепіпеда з вимірами 2, 3 і 3 м. Скільки кубометрів землі вийняли?

Задача 4. Каністра має форму прямокутного паралелепіпеда, виміри якого     2, 3 і 4 дм. Скільки літрів бензину вміщується в ній? (1 л = 1 дм³)

Такі задачі сприяють формуванню і закріпленню в уяві дітей предметів, які мають і можуть мати форму певної геометричної фігури чи тіла. Тому задачі, в яких немає прямого співставлення об’єкта і його математичного еквівалента, в подальшому будуть розв’язуватися значно легше.

Формування навичок побудови діаграм у 6 класі я пропоную здійснювати у такій послідовності:

1. Побудова лінійних або стовпчастих діаграм, в яких певне значення величини чи визначена кількість об’єктів позначається однією клітинкою.
2. Побудова лінійних або стовпчастих діаграм з використанням масштабу.
3. Побудова кругових діаграм.
4. Побудова діаграм за допомогою комп’ютера.

Варто продемонструвати школярам весь цикл роботи від отримання повідомлення до його дослідження шляхом побудови різних діаграм, так як вони слугують одним із засобів зв’язку математики з життям, оскільки відображають дані, взяті із повсякденного життя. Діаграми є не лише зручним засобом унаочнення, дозволяючи в простій і доступній для сприймання формі показати співвідношення між величинами та виразити характер зміни тієї чи іншої величини, а й допомагають на пропедевтичному рівні ознайомити учнів з прямокутною системою координат і графіками функцій.

Таким чином, навчання учнів 5–6 класів математики із врахуванням вищезазначених методичних рекомендацій сприятиме формуванню у них:

• уявлення про числовий і буквенний вираз, рівняння як знако-символьну модель;
• уявлення про кілька видів образних моделей: схеми, таблиці, малюнки, зображення геометричних фігур та тіл, діаграми;
• уявлення про деякі властивості моделі;
• елементарні навички застосування методу математичного моделювання.

 

Початковий етап вивчення математичного моделювання

 

Аналіз масової практики навчання учнів в основній школі засвідчив, що вивчення геометрії відбувається, як правило, без проектування на реальні об’єкти та життєві ситуації. У переважній більшості випадків від учнів вимагається лише відтворення теоретичного матеріалу та його застосування під час розв’язування абстрактних задач. Я пропоную навчати школярів геометрії з використанням математичного моделювання. Продемонструю це на прикладі вивчення основних змістових ліній курсу, зокрема “Геометричні фігури та їх властивості” і “Геометричні величини”.

Геометричні фігури та їх властивості – традиційно одна з провідних змістових ліній шкільного курсу геометрії. Це викликано тим, що використовуватимуть їх учні постійно у процесі вивчення предмету, у практичній діяльності вдома та у майбутній професійній діяльності.

З найпростішими геометричними фігурами та деякими їх властивостями на наочно-інтуїтивному рівні школярі ознайомлюються вже у початковій школі та в 5–6 класах.

Систематичне ж вивчення цієї змістової лінії відбувається у 7–9 класах. Спочатку узагальнюються наочні уявлення про найпростіші фігури, вводяться первісні поняття, формулюються аксіоми, потім вивчаються ознаки рівності трикутників, які разом з ознаками паралельності є основним аргументом під час доведення теорем та розв’язування задач. Далі вивчення трикутників відбувається протягом усього курсу планіметрії. Також учні ознайомлюються з поняттям кола, круга, їх елементами та властивостями. Однією з найбільших тем змістової лінії є “Чотирикутники”, методичні особливості якої з точки зору навчання школярів математичного моделювання ми і розглянемо далі.

Я пропоную змінити порядок вивчення матеріалу і ознайомити учнів зі всіма видами чотирикутників одночасно: спочатку ввести означення, потім властивості та ознаки.

Такий підхід дозволяє значно зменшити час на вивчення нового матеріалу. Так як властивості різних видів чотирикутника легко побачити на малюнку, а їх доведення ґрунтується на ознаках рівності трикутників, з якими школярі добре знайомі, немає необхідності послідовно доводити всі властивості. Достатньо буде, якщо кожен учень самостійно доведе принаймні дві-три властивості. При цьому з’являється можливість приділити увагу розв’язуванню різних видів задач: на обчислення, на доведення, на побудову.

На закріплення видів чотирикутників слід запропонувати школярам знайти на малюнках та в навколишньому середовищі предмети, моделями яких вони є.

Якщо для учнів це завдання виявиться складним, можна надати їм підказку:

“У повсякденному житті форму чотирикутника мають рами велосипедів, мотоциклів, де для жорсткості проведена діагональ.

У фізиці застосовують паралелограм при вивченні розкладання сил, при знаходженні рівнодіючої сили.

Форму прямокутника мають стіни будинків, підлога, стеля, грані олівців тощо.

У хірургічному відділенні для пересадки шкіри застосовують спеціальний апарат, який вирізає шкіру у вигляді квадратів. Їх розташовують на обпаленій ділянці в шаховому порядку, а так як шкіра має властивість рости у всіх напрямках, з часом проміжки між квадратами заростають.

У сільському господарстві застосовують квадратно-гніздовий спосіб посадки культур задля отримання кращого врожаю.

Рейковий домкрат для легкових автомобілів має форму ромба.”

Слід акцентувати увагу на тому факті, що вищевказані об’єкти, незважаючи на їхні розміри, колір, матеріал, з якого вони виготовлені тощо, є прообразами вивчених геометричних фігур. На цьому етапі навчання школярам доцільно дати означення математичної моделі, тобто: “Математична модель – це опис досліджуваного об’єкта, процесу чи деякої ситуації мовою математичних понять, формул, рівнянь, відношень тощо”.

Учителю необхідно досягти того, щоб термін “математична модель” став звичним для учнів і використовувався у потрібних ситуаціях без зусиль та з достатньою свободою. При цьому слід домагатися правильного співвідношення між внутрішнім змістом поняття та його зовнішнім вираженням.

Також варто ознайомити школярів із видами моделей та запропонувати їм навести відповідні приклади.

Таким чином, використання моделей у процесі вивчення видів чотирикутників, їх властивостей та ознак сприяє унаочненню навчального матеріалу, а отже, і глибокому розумінню його суті та свідомому засвоєнню.

Розглянемо застосування моделювання у процесі розв’язування задач.

Для усвідомлення можливості використання властивостей чотирикутників у повсякденному житті та з метою проведення профорієнтаційної роботи з учнями, їм варто запропонувати завдання типу:

1. Дано дошку з паралельними краями. Тесляреві потрібно відрізати кінець дошки під кутом 45˚. Як це зробити без транспортира?
2. Як будівельнику, не вимірюючи кутів чотирикутної земельної ділянки, відведеної під фундамент будинку, пересвідчитися, що вона має форму прямокутника?
3. Столяр, щоб перевірити, чи має стільниця форму квадрата, виміряв довжину кожної зі сторін і побачив, що вони рівні. Чи правильна така перевірка? Чи достатньо виміряти діагоналі стільниці та переконатися, що вони рівні?
4. Чотири виробничі об’єкти на будівельному майданчику розміщені у вершинах опуклого чотирикутника. У якому місці слід побудувати завод будівельних матеріалів, щоб сума відстаней від нього до всіх виробничих об’єктів була найменшою?
5. Швачка викроїла з тканини чотирикутник, який повинен мати форму ромба. Як перевірити правильність виготовлення викрійки, не користуючись інструментами?

Подібні завдання сприяють розвитку не лише уміння співставляти реально існуючий об’єкт з його математичним еквівалентом (образною моделлю), а й переносити властивості геометричної фігури на її реальний прообраз (здійснювати інтерпретацію математичних фактів).

Щоразу під час розв’язування прикладних задач учням слід наголошувати, що при створенні математичної моделі, зокрема, образної, реально існуючого об’єкта використовуються правдоподібні міркування. Вибір тих чи інших геометричних фігур, як інтерпретації описаних в умові реальних об’єктів, може бути недостатньо строгим та обґрунтованим. Так, наприклад, при розв’язуванні задачі “Усередині Верхнього ставу (дендропарк “Софіївка”), який має форму круга, міститься Острів кохання. Укажіть найкоротший маршрут катера, що з’єднує будь-які дві точки берега і має проміжний причал біля острова” за став круглої форми приймаємо круг, хоча в дійсності не існує водойми точної круглої форми, навіть якщо вона створена штучно. У той самий час під час розв’язування задачі “Як має проходити магістраль, щоб відстані від неї до кожного з трьох даних населених пунктів були однаковими? Укажіть розташування пунктів, при якому ця відстань мінімальна” за населені пункти, що за розмірами майже завжди перевершують розміри ставу, ми приймаємо точки.

Все це робить розв’язок прикладної задачі правдоподібним. Крім того, під час розв’язування задачі в межах математичної моделі часто використовуються наближені обчислення, що, в свою чергу, теж впливає на результат.

У такому разі можна говорити про зовнішню та внутрішню правдоподібність моделі. Зовнішня характеризує адекватність моделі реальній життєвій ситуації, а внутрішня визначає можливість застосування математичних методів до описаної в задачі проблеми. Тому під час розв’язування прикладних задач слід знаходити розумне співвідношення цих правдоподібностей, адже прагнення до високої зовнішньої правдоподібності призводить, як правило, до виникнення досить громіздких обчислень і, навпаки, побудова простої математичної моделі може спричинити значну похибку отриманого результату.

Продемонструємо застосування методів математичного моделювання до розв’язування задач.

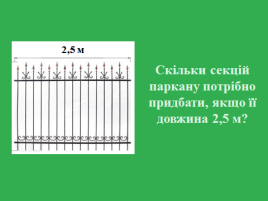
Задача 5. Земельну ділянку розміром 30м×50м необхідно обнести металевим парканом, залишивши 4 м на ворота та хвіртку. Скільки секцій паркану потрібно придбати, якщо її довжина 2,5 м?

І. Побудова математичної моделі

Хоча в задачі йде мова про об’єкти добре відомі учням, варто продемонструвати їх на мультимедійній дошці (див. мал. 1).

 

 

Потім учитель має надати учням пояснення такого плану:

Геометрія – це наука, яка використовує ідеалізовані поняття, такі як “пряма”, “площина”, “квадрат”, “куля” і т.д. Усі реальні прообрази цих понять насправді мають на своїй поверхні певні нерівності, а деякі з них навіть дещо відхиляються від “ідеальної” форми. І якби ми в обчисленнях враховували такі дрібниці, вони були б дуже громіздкими та вимагали великих затрат часу. Саме тому ми вивчаємо ідеальні форми реальних об’єктів, і хоча отримані формули при застосуванні їх до предметів навколишньої дійсності дають наближений результат, він є достатнім для практичних потреб.

Подальшу роботу над задачею можна провести у формі фронтальної бесіди:

Учитель: Форму якої геометричної фігури має земельна ділянка?

Очікувана відповідь: Оскільки в умові задачі вказано два виміри ділянки, то це прямокутник.

Учитель: Що слід знайти, щоб дати відповідь на запитання задачі?

Очікувана відповідь: Щоб знайти кількість металевих секцій паркану, необхідно спочатку обчислити довжину самого паркану.

Учитель: Як це можна зробити?

Очікувана відповідь: Для цього варто знайти периметр ділянки, тобто периметр прямокутника:

Учитель: Знаючи тепер довжину паркану, як знайти кількість його секцій?

Очікувана відповідь: Щоб відповісти на запитання задачі, слід обчислити довжину паркану без воріт та хвіртки і отримане число поділити на довжину однієї секції, тобто

Учитель: Отже, вираз є знако-символьною моделлю задачі.

ІІ. Розв’язування задачі в межах математичної моделі.

Обчисливши значення числового виразу, отримуємо:

ІІІ. Інтерпретація отриманого розв’язку

Оскільки придбати 62,4 секцій металевого паркану неможливо, то округлюємо результат з надлишком і отримуємо 63 секції.

Отже, для того щоб земельну ділянку розміром 30м×50м обнести металевим парканом, залишивши 4 м на ворота та хвіртку, необхідно придбати 63 секції, довжиною 2,5 м.

Подібні задачі слід пропонувати учням якомога частіше, оскільки їх розв’язування сприяє не лише засвоєнню теоретичного матеріалу, а й обґрунтуванню необхідності його вивчення для подальшого застосування у повсякденному житті.

Поняття величини є одним із найважливіших не лише в математиці, а й у повсякденному житті. Це пов’язано з тим, що крізь призму величин описуються реальні властивості об’єктів та явищ, відбувається пізнання навколишньої дійсності, тобто здійснюється перехід від описового до кількісного вивчення характеристик (математизація знань про природу).

Геометричні величини (довжина, градусна міра кута, площа, об’єм) допомагають встановити як міжпредметні зв’язки (з фізикою, хімією, економікою і т.д.), так і внутрішньопредметні – з числовими системами. Наявність великої кількості життєвих та професійних ситуацій, в яких необхідно виміряти величину чи обчислити її значення за формулою, зумовлює виокремлення геометричних величин в одну з найважливіших змістових ліній шкільного курсу математики, вивчення якої є наскрізним.

Пропедевтика змістової лінії відбувається у початкових та 5–6 класах і передбачає формування на інтуїтивному рівні уявлень про величини, їх властивості та розвиток навичок практичного вимірювання, а також введення формули обчислення площі прямокутника і об’єму прямокутного паралелепіпеда.

В основній школі відбувається ознайомлення школярів із аксіомами вимірювання довжин відрізків і градусних мір кутів, поняттям площі, об’єму та їх властивостями; відпрацювання навичок розв’язування відповідних задач.

Розглянемо методику вивчення кожної геометричної величини, що входить у курс геометрії основної школи окремо.

І. Довжина. У шкільному курсі геометрії довжина як величина вивчається стосовно таких фігур: відрізка, кола, їх частин та об’єднань.

Вивчення довжини відрізка починається з перших уроків геометрії, коли учні знайомляться з найпростішими геометричними фігурами.

Оскільки в курсі математики 5 класу школярі у неявному вигляді знайомляться з правилами вимірювання довжин відрізків, ми пропонуємо відразу сформулювати означення довжини відрізка та визначити властивості, які воно задовольняє. Для цього необхідно нагадати учням, як відбувається процес вимірювання довжини відрізка. Варто наголосити на тому, що спочатку із множини відрізків слід вибрати відрізок, довжина якого вважається рівною одиниці та визначити, скільки разів одиничний відрізок повністю вкладається у заданому відрізкові. Може виявитися, що відрізок, прийнятий за одиницю виміру, не вкладається ціле число разів у заданому відрізку – є залишок. Тоді одиничний відрізок ділять на рівні частини, зазвичай на 10 рівних частин, і визначають, скільки разів одна така частина вкладається в залишку. Але можливо, що і взята частина одиниці виміру не вкладається в залишку ціле число разів, і отримується новий залишок. Тоді для більш точного вимірювання заданого відрізка вказану частину одиничного відрізка можна розділити на 10 рівних частин і продовжити процес вимірювання. Подумки цей процес можна продовжувати і далі, вимірюючи довжину відрізка з усе більшою точністю. На практиці, однак, слід наголосити учням, користуються наближеними значеннями довжин відрізків, тобто вимірюють довжину відрізка з точністю до поділки шкали вимірювального інструменту.

Підсумовуючи вище вказане, вчитель може запропонувати учням наступне означення довжини відрізка:

Довжина відрізка – це число, що показує, скільки разів одиничний відрізок і його частини укладаються в даному відрізку.

З цього означення випливають основні властивості довжини відрізка:

• Кожен відрізок АВ має невід’ємну довжину, причому ця довжина нульова тоді і тільки тоді, коли точки А і В співпадають.
• Якщо точка С належить до відрізка АВ, то довжина відрізка АВ дорівнює сумі довжин відрізків АС і СВ.

З основних властивостей довжини відрізка випливають її інші властивості, зокрема:

• Рівні відрізки мають рівні довжини.
• Якщо відрізок АВ складається із скінченної кількості відрізків без спільних внутрішніх точок, то довжина відрізка АВ дорівнює сумі довжин цих відрізків.
• Якщо відрізок АВ є частиною відрізка CD і АВ та CD не є рівними, то довжина відрізка АВ є меншою за довжину відрізка CD.

ІІ. Площа. Систематичне вивчення площ відбувається у 8 – 9 класах.

Програмою визначена така послідовність тем:

1. Площа прямокутника, паралелограма, ромба, трикутника (за стороною та висотою, проведеною до неї).
2. Площа трапеції.
3. Площа трикутника (за формулою Герона, за двома сторонами і кутом між ними, за радіусами вписаного і описаного кола).
4. Площа круга та його частин.

Поняття площі довільної фігури у підручниках не вводиться, основна увага приділена виведенню формул площ конкретних фігур.

Зупинимося на площі чотирикутників.

Основою для виведення формул площ окремих видів чотирикутників є площа прямокутника. У діючих підручниках теорема про площу прямокутника доводиться для двох випадків: якщо довжини сторін виражаються натуральними числами; якщо довжина хоча б однієї із сторін є дробовим або ірраціональним числом. Однак наведені доведення досить важко сприймаються учнями і, як свідчить практика роботи у школі, не усвідомлюються ними. Ми пропонуємо дещо інший шлях виведення формули для обчислення площі прямокутника, який ґрунтується на використанні методу неповної індукції.

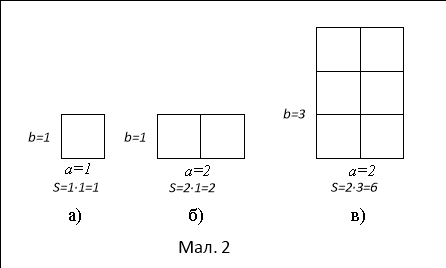
Розглянемо прямокутник, сторони якого рівні 1 (див. мал. 2 а)). Очевидно, що його площа дорівнює одиниці. Назвемо цей прямокутник одиничним квадратом.

Розглянемо тепер прямокутник, який складається з двох одиничних квадратів (див. мал. 2 б)). Зрозуміло, що його площа буде рівною 2. Оскільки сторони цього прямокутника рівні 2 і 1, то S=2·1=2. Аналогічні міркування проведемо стосовно прямокутника, який складається з 6 одиничних квадратів (див. мал. 2 в)). Отримаємо S=2·3=6. Ці приклади дають підставу стверджувати, що площа довільного прямокутника з вимірами a та b визначається за формулою S= a·b. 

Після цього вчитель має переконатися з учнями, що для площі прямокутника, яка визначена за формулою S = a·b, виконуються основні властивості площі.

Для 12 – 13-річних школярів, враховуючи їхні вікові особливості, вище наведене доведення є досить зрозумілим, оскільки застосовуються образні моделі.

Першочерговими завданнями на початковому етапі навчання учнів методам математичного моделювання є формування вмінь: виділяти суттєві характеристики об’єкта, процесу чи явища, що досліджується; обирати доцільну модель до задачі; виявляти і оцінювати ступінь точності отриманих результатів; поширювати знайдений спосіб розв’язання на подібні прикладні задачі.

У такій ситуації корисними будуть так звані задачі-»вкладки», що передбачають побудову на базі однієї елементарної задачі системи завдань, розв’язання кожного з яких потребує залучення нових знань, активізації додаткових умінь та навичок. Наприклад:

Задача 6. Класна кімната має розміри 5×8м. Знайдіть її площу.

Ця задача є елементарною, тому досить простими будуть для неї і математичні моделі (образна та знако-символьна), однак поставлені додаткові запитання дають змогу розкрити її прикладні можливості, збагатити і ускладнити модель. Зокрема:

1. Які ще лінійні розміри можуть бути у кімнати, яка рівновелика даній?
2. Чи існує в реальному житті кімната, один із лінійних розмірів якої дорівнює 1 м?
3. Як зміниться значення площі кімнати, якщо значення довжини кожної з її сторін збільшити удвічі?
4. Як зміняться значення лінійних розмірів кімнати, якщо значення її площі збільшити у 1,5 рази?

Запитання 1 – 2 формують в учнів розуміння реального походження даних, тобто дозволяють ситуацію, існуючу в математиці, перенести в реальну дійсність і з’ясувати її достовірність.

Запитання 3 – 4 сприяють засвоєнню структури формули для обчислення площі прямокутника.

Пропонуємо систему задач, створену на основі задачі 6.

Задача 7. Підлога класної кімнати має розміри 5×8м. Скільки банок фарби вагою 1 кг необхідно для фарбування підлоги, якщо витрати фарби на 1м² дорівнюють 120 г?

Задача 8. Якщо в кімнаті довжиною 8 м та шириною 5 м фарбувати нову підлогу, то технологія вимагає робити це тричі. Витрати для першого разу складають 150 г на м², для другого – 120 г на м², для третього – 70 г на м². Які загальні витрати фарби?

Задачі 7 і 8, незважаючи на спільність геометричної моделі, мають різні алгебраїчні представлення, а отже, і знако-символьні моделі у них будуть різні.

Розв’яжемо задачу 8.

І. Побудова математичної моделі

Так як у підлітків 13 років гарно розвинене наочно-образне мислення та уява, але не на високому рівні сформовані навички абстрактної побудови математичної моделі до задачі, варто запропонувати їм ряд додаткових запитань:

1) Форму якого геометричного тіла має класна кімната?

2) Яку форму має підлога класної кімнати?

Отримавши відповіді, учитель пропонує школярам абстрагуватися від можливих нерівностей підлоги у класній кімнаті та представити її у формі прямокутника, таким чином ідеалізувавши ситуацію. До речі, образну модель до цієї задачі будувати не обов’язково, оскільки учні, перебуваючи у класній кімнаті, добре уявляють, про що йде мова.

Таким чином, у результаті маємо прямокутник зі сторонами 5 м і 8 м. Для того щоб знайти вагу фарби, необхідної для покриття підлоги, слід спочатку знайти площу отриманого прямокутника. Отже, числовий вираз і буде шуканою знако-символьною моделлю.

II. Розв’язування задачі в межах математичної моделі

 Маємо:

III. Інтерпретація одержаного розв’язку

Отже, загальні витрати фарби на підлогу класної кімнати становлять   13600 г або 13,6 кг.

Після розв’язання цієї задачі варто задати учням кілька додаткових запитань типу:

1.     Скільки банок фарби слід придбати, якщо вага однієї банки 0,75 кг?
2.     Яку найменшу кількість банок фарби потрібно придбати, якщо в наявності є банки вагою 0,8 кг, 1,5 кг та 2 кг? 

Такі запитання сприятимуть різносторонньому аналізу ситуації та вибору можливих шляхів її вирішення.

Наступні задачі стосуються проблем покриття підлоги.

Задача 9. Розміри паркетної дощечки 0,07×0,5м. Скільки упаковок дощечок потрібно для покриття підлоги у класній кімнаті, довжина якої 8 м, а ширина – 5 м? В упаковці містить 250 паркетних дощечок.

Задача 10. Довжина класної кімнати 8 м, а ширина – 5 м. Лінолеум без малюнка продається в рулонах завширшки 2 м. Скільки метрів лінолеуму необхідно придбати, щоб покрити всю підлогу?

Розв’язання цих задач передбачає розгляд різних варіантів покриття підлоги і необхідність здійснення вибору на користь одного із них за певним критерієм (естетичності, економності матеріалу чи грошових ресурсів, часу тощо).

Задача 11. Довжина класної кімнати 8 м, а ширина – 5 м. Лінолеум без малюнка продається в рулонах завширшки 1,5 м або 2,5 м. Скільки метрів лінолеуму і з якого рулону необхідно придбати, щоб покрити всю підлогу?

Модифікувати дану задачу можна, використавши запитання:

1. Скільки метрів лінолеуму завширшки 1,5 м (2,5 м) необхідно придбати, щоб покрити всю підлогу з найменшою довжиною швів?
2. Скільки метрів лінолеуму завширшки 1,5 м (2,5 м) необхідно придбати, щоб покрити всю підлогу з найменшою кількістю відходів? і т.д.

Такі задачі змушують учнів моделювати кілька можливих варіантів розв’язання (створювати різні образні моделі), аналізувати, обговорювати їх, приймати рішення, виходячи з власного життєвого досвіду. Це, в свою чергу, сприяє формуванню вміння обирати доцільну модель до задачі.

Загалом задачі-»вкладки» яскраво демонструють процес ускладнення математичної моделі, сприяють удосконаленню навичок математичного моделювання та якісному формуванню в учнів загальнологічних прийомів розумової діяльності, хоча і вимагають від учителя додаткових зусиль та часу.

Також доцільним, на мою думку, є розв’язування задач з недостатніми або надлишковими даними.

Задача 12. Проведіть необхідні вимірювання і розрахуйте, яку кількість квадратних плит зі стороною 0,6 м необхідно придбати для монтування підвісної стелі у кімнаті у вас вдома.

Це задача із недостатніми даними. Для її розв’язання необхідно знати розміри кімнати. І якщо образну модель до даної задачі побудувати легко, то створення знако-символьної може викликати труднощі. Враховуючи той факт, що значення недостатніх даних можна, як правило, взяти або ж з відповідної таблиці, або завдяки безпосереднім вимірюванням (як у задачі 10), слід звернути увагу школярів на можливість отримання похибки і необхідність її врахування.

Поступово зменшуючи кількість даних, учням варто запропонувати розв’язати задачі взагалі без заданих числових даних.

Задача 13. Розрахуйте, яку кількість рулонів шпалер (без підгонки малюнка) необхідно придбати для ремонту класної кімнати.

Подібні задачі сприяють формуванню в учнів навичок пошукової діяльності, комунікативних, вимірювальних та обчислювальних умінь.

Задачі з надлишковими даними виховують в учнів звичку більш вдумливо будувати зв’язки між даними і шуканими величинами, правильно здійснювати вибір математичної моделі.

Задача 14. Шкільний спортивний зал має розміри 18×9×6м (д×ш×в). Яка максимальна кількість школярів може одночасно перебувати у ньому, якщо норма на одного учня 1,25 м²?

Отже, по закінченню вивчення курсу геометрії у 7–8 класах можна очікувати, що в учнів будуть сформовані:

• розширені уявлення про планіметричні фігури як математичні моделі;
• навички побудови кількох видів образних моделей: схем, таблиць, малюнків, зображень геометричних фігур та їх комбінацій;
• розширені уявлення про деякі властивості моделі;
• навички застосування методів математичного моделювання до доведення теорем і розв’язування задач.

 

Основний етап вивчення математичного моделювання

 

Чинний Державний стандарт базової і повної загальної середньої освіти не виділяє у якості окремої змістової лінії “Декартові координати та вектори на площині”. Однак розгляд цієї теми має велике значення у процесі формування в учнів знань, умінь та навичок математичного моделювання, оскільки дає можливість ознайомити школярів з новими видами моделей та способами їх використання.

У програмі вищевказані теми вивчаються окремо і є розділеними в часі темою “Геометричні перетворення”. На мою думку, доцільно вивчати їх послідовно, починаючи з “Декартових координат на площині”, оскільки вони нерозривно пов’язані між собою.

Пропедевтика понять “координата точки”, “координатна площина” починається вже у 5 класі, де вивчається координатний промінь і позначаються натуральні та дробові числа на ньому. Потім у 6 класі для зображення додатних та від’ємних чисел вводиться координатна пряма і виконуються вправи на знаходження координати точки та точки за її координатою. Лише після цього учні знайомляться з поняттям “прямокутна система координат на площині”.

Знайомство доцільно розпочати із життєвої ситуації, добре знайомої кожному учневі: пошук власного місця у залі кінотеатру, актовій залі тощо. Також варто запропонувати школярам самостійно навести приклади використання системи координат у житті. Наприклад:

• Граючи в “морський бій”, ми користуємося такою системою координат: кожна клітинка на ігровому полі визначається літерою і цифрою, зокрема літерами позначаються вертикалі ігрового поля, а цифрами – горизонталі.
• Схожа система координат є на шахівниці: горизонталі позначаються латинськими літерами, а вертикалі – цифрами.
• На квитках у цирк, на потяг, у театр тощо дано опис того, де знаходиться місце власника даного квитка: на квитках у цирк і в театр – це номер ряду і номер місця в цьому ряду, а на квитку на потяг – номер вагона і номер місця в цьому вагоні.

Надалі здобуті знання активно використовуються в курсі алгебри               7–9 класів під час побудови графіків функцій.

Вивчення у 9 класі теми “Декартові координати на площині” слід починати з повторення і узагальнення здобутих раніше знань та умінь. Зробити це можна у вигляді фронтального опитування:

1. Координатною площиною називається площина, на якій ... (задана прямокутна система координат).

2. Систему координат утворюють ... (дві взаємно перпендикулярні координатні прямі).

3. Області, на які вісі розбивають координатну площину, називають ... (координатними чвертями).

4. Координатна пряма Ох називається ... (вісь абсцис).

5. Координатна пряма Оу називається ... (вісь ординат).

6. Положення точки на координатній площині визначається … (двома координатами).

7. Перша координата точки називається ... (абсциса).

8. Друга координата точки називається ... (ордината).

9. Якщо абсциса точки дорівнює нулю, то точка лежить ... (на вісі ординат).

10. Якщо ордината точки дорівнює нулю, то точка лежить ...(на вісі абсцис).

11. Якщо обидві координати точки рівні нулю, то точка лежить ... (на початку координат).

Після цього варто запропонувати учням позначити на координатній площині точки за заданими координатами, визначити координати заданих точок, навести приклади застосування координат у повсякденному житті (для моделювання ескізів промислових машин, устаткування, об'єктів на місцевості; під час проведення досліджень в галузі хірургії,  виконання флюорографії, різноманітних знімків органів, кардіограм; у таблиці Менделєєва кожен елемент має своє місце в групі і підгрупі (координати елемента) тощо).

Подальше виведення формул для знаходження відстані між двома точками та координат середини відрізка особливих труднощів у школярів не викликає. На даному етапі вчителю слід звернути увагу учнів на той факт, що поняття “відстань між двома точками А(х₁;у₁) і В(х₂;у₂)” має дві математичні моделі: образну – відрізок АВ, довжину якого необхідно знайти, та знако-символьну – формулу АВ = .

Розв’язування задач передбачає виконання арифметичних дій за виведеними формулами, однак слід продемонструвати школярам і практичне застосування даного матеріалу. Наприклад, детально розглянути такі задачі:

Задача 15. Основу драбини довжиною 6 м відсунуто від стіни на 1 м. На скільки знизиться верхній кінець драбини, якщо основу відсунути ще на 0,5 м? Розв’яжіть задачу, використовуючи систему координат.

Задача 16. Два туристи, які знаходяться на відстані 100 м один від одного, одночасно почули вигук керівника групи. На якій найменшій відстані від кожного з них міг перебувати керівник у момент вигуку, якщо точно посередині між туристами стоїть дерево, яке в обхваті має 2,5 м?

Задача 17. Снаряд був запущений у точку А(5, 6). Під час польоту сталося відхилення: снаряд упав у точці В(7, 9) і вибухнув. Радіус ураження снаряду      5 км. Визначити, на яку відстань відхилився снаряд від заданої точки і чи виявилася ціль ураженою. Скласти рівняння кола, в межах якого снаряд зберігає вражаючу дію.

Задача 18. З літака вистрибнув десантник і приземлився в точці    В(5, 0), потім вийшов на базу супротивника в точку С(1, 0). Після здійснення диверсії десантник прибув у вказане місце зустрічі в точку D(-2, 0). Через 20 хвилин його підібрав вертоліт К–60 “Ластівка”. Визначити шлях, пройдений десантником.

Задача 19. Двом розвідникам було наказано з пункту А перейти в пункт D. Перший пішов по маршруту А(3, 3) – В₁(0, 0) – С₁(3, 4) – D(-5, 3), а другий по маршруту А(3, 3) – В₂(1, -3) – С₂(-4, 0) – D(-5, 3). З'ясувати, хто швидше прибуде в пункт D, якщо швидкість першого дорівнює 5 км/год, швидкість другого – 3,5 км/год?

У процесі їх розв’язування варто наголосити учням, що система координат – це самостійна математична модель, за допомогою якої розв’язується цілий спектр задач та вивчаються інші моделі, зокрема вектори. Також слід озброїти школярів алгоритмом застосування методу координат, який по своїй суті досить близький з методом математичного моделювання:

1. перевести умову задачі зі звичайної мови на мову координат;
2. розв’язати задачу мовою координат;
3. здобутий результат перевести на мову, якою сформульована задача.

Найбільш складним є перший етап алгоритму, який включає вміння: обирати зручну систему координат, складати рівняння заданих фігур, визначати координати заданої точки, будувати точку за заданими координатами.

Якщо останнім трьом вище наведеним умінням у школі приділяється достатньо часу, то вибір системи координат залишається поза увагою, хоча це – один із найважливіших моментів методу координат, який визначає в подальшому його результативність. Обирати систему координат слід так, щоб алгебраїчні викладки при цьому були найпростішими, інакше досить легку задачу можна зробити нерозв’язною. Тому на нашу думку, починаючи з              6 класу, необхідно формувати в учнів уявлення про можливість довільного вибору системи координат, пропонуючи їм завдання виду:

1. Довжина відрізка 4 см. Оберіть систему координат так, щоб кінці відрізка визначалися найпростіше.
2. Довжина відрізка 6 см. Оберіть систему координат так, щоб його початок мав координати (-3;0).
3. Побудуйте квадрат зі стороною 2 см і позначте в ньому точку. Оберіть систему координат так, щоб задана точка мала координати: а) (1;1); б) (-1;1);      в) (1;-1).
4. Побудуйте довільний прямокутний трикутник. Оберіть систему координат так, щоб координати його вершин визначалися найпростіше.

Сформовані на високому рівні вище наведені вміння дозволять розв’язувати не лише класичні задачі на застосування методу координат, а й нестандартні.

Після вивчення теми “Декартові координати на площині” варто опрацювати тему “Вектори на площині”.

Особливі проблеми у школярів викликає розуміння поняття “вектор”, оскільки воно є досить абстрактним. З метою мотивації варто нагадати учням, що з векторними величинами вони зустрічалися раніше в курсі фізики 7 класу, вивчаючи силу, переміщення, швидкість, прискорення тощо. Саме тоді зазначалося, що величини, які окрім числового значення, мають напрям називаються векторними. Також доцільно розповісти школярам про широкий спектр використання векторів у різних сферах життєдіяльності людини. Зокрема:

•     У фізиці будь-яка сила розкладається за векторами. Це використовується під час виконання розрахунків у будівництві різних споруд, літаючих апаратів, у навігації морського і повітряного флоту.
•     У біології вектором називається організм, клітина, вірус, плазміда або інший біологічний об'єкт, що несе потенційно активний елемент. Наприклад, щури переносять збудників чуми, а кліщі є переносниками вірусу, що викликає енцефаліт.
•     Вектор у генній інженерії – це автономна молекула ДНК, яка бере участь у перенесенні генів від організму-донора в організм-реципієнт, а також у клонуванні нуклеїнових послідовностей (клонуючий вектор).
•     За допомогою векторів синтезуються різні ліки, зокрема антибіотики, ферменти та навіть цілі каскади ферментів, необхідні людині (наприклад, інсулін).
•     У генній інженерії існує молодий напрямок, який називається генотерапія, де вектори дозволяють виправляти генетичні дефекти.
•     Вектори застосовуються також при клонуванні.

Прослухавши повідомлення, учні відмічають той факт, що вектори у різних науках мають одну спільну рису: вони напрямлені.

У більшості діючих підручників з геометрії вектор і визначається як напрямлений відрізок. Таке визначення легко запам’ятовується, але як показує практика, не сприяє усвідомленню поняття. Тому перш за все слід наголосити школярам, що вектор – це математична абстракція об’єктів, що характеризуються величиною і напрямом, тобто їх математична модель.

У геометрії вектор визначається двома точками, одна з яких є його початком, а інша – кінцем. Відстань між цими точками і є довжиною вектора. Наступним по важливості є введення поняття рівності векторів. Слід запропонувати учням наступне означення: “Ненульові вектори називаються рівними, якщо вони: 1) співнапрямлені; 2) мають однакову довжину”. Необхідно формувати в учнів розуміння рівності векторів по аналогії з рівністю чисел 0,2; ; і т.д., тобто рівні вектори можуть мати різні форми запису завдяки різним початкам та різним кінцям, як і різні форми запису одного і того ж числа.

Значні труднощі в учнів викликає введення координат вектора. Основною причиною цього є невідповідність сформованого у свідомості школярів поняття координат точки, які “прив'язують” її до координатної площини, і тим, що нескінченно багато векторів, розташованих в різних місцях координатної площини, мають одні й ті ж координати. Уникнути труднощів можна, знову ж таки провівши аналогію з числами: рівні, але різні за формою запису числа на координатній площині визначаються однозначно, так і рівні, але різні за розміщенням вектори мають однакові координати. Слід вказати учням і на той факт, що вектор як напрямлений відрізок – це образна модель, вектор як упорядкована пара точок – знако-символьна модель одного і того ж поняття.

Загалом координати вектора дають змогу означити дії над векторами, довести їхні властивості, застосовувати до розв’язування задач і встановити зв’язок між геометричною інтерпретацією вектора і його алгебраїчним вираженням, тобто між його образною та знако-символьною моделями.

Під час вивчення теми “Вектори на площині” слід пропонувати школярам мультимедійні презентації, оскільки основна їх перевага – це наочність, компактність та інтерактивність подачі матеріалу. Особливо корисними вони будуть, коли необхідно продемонструвати властивості векторів, рівність векторів на координатній площині, побудувати  малюнок до задачі тощо.

У процесі розв’язування задач, як на доведення, так і на обчислення,слід звернути увагу школярів на те, що векторний метод не є універсальним. Його зручно застосовувати для доведення паралельності чи перпендикулярності прямих, для визначення довжини відрізка чи градусної міри кута і т.д.

З векторним методом доведення геометричних тверджень варто ознайомити учнів на прикладі тих тверджень, які школярі вміють доводити без використання векторів. Наприклад, твердження про властивість середньої лінії трикутника чи трапеції, діагоналей ромба чи квадрата, суму квадратів діагоналей паралелограма, теорема косинусів тощо. Довівши кілька таких тверджень, учні самостійно або з допомогою вчителя мають виділити алгоритм застосування векторного методу, який за своїми етапами схожий на метод математичного моделювання.

Після відпрацювання навички виконання дій з векторами слід запропонувати школярам кілька задач прикладного характеру, як правило, вони тісно пов’язані з фізикою.

Задача 20. Група туристів вирішила прогулятися вздовж річки. Спочатку вони пройшли на південь 300 м. Після того, як перетнули міст, вирушили вздовж річки в південно-східному напрямку і подолали ще 200 м. Яке переміщення здійснили туристи? Який шлях вони подолали?

Задача 21. Під яким кутом потрібно направити човен до берега, щоб перебратися на другий берег річки найкоротшим шляхом, коли відомо, що власна швидкість човна 25 м/хв, швидкість течії 10 м/хв, а ширина річки         250 м? Як довго відбуватиметься переправа?

Задача 22. На тіло вертикально вверх діє сила 5Н, а вертикально вниз – сила 7Н. Знайдіть графічно рівнодіючу силу.

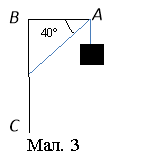
Задача 23. До кінця кронштейна (див.мал.3) підвішений ліхтар вагою 18 кг. Знайти силу розтягування стрижня АВ і силу стиснення стрижня ВС.

Задача 24. Двоє коней біжать берегами каналу і тягнуть важку баржу паралельно. Чому дорівнює сила опору води, якщо канати натягнуті з силами 600 Н і 700 Н, а кут між ними дорівнює 60 °?

Задача 25. Велосипедист рухається зі швидкістю 15 км/год у північному напрямку, і йому здається, що південно-східний вітер зі швидкістю 9 км/год направлений до нього під кутом 15º. Знайти справжній напрям вітру.

Застосування векторів до розв’язування задач сприяє формуванню в учнів навичок абстрагування та дослідницької роботи, встановленню міжпредметних зв’язків, а також підвищенню загального рівня математичної культури.

Ще однією важливою складовою в системi навчання школярів методам математичного моделювання є написання розрахунково-графічних та наукових робіт в системі МАН за тематикою, пов’язаною з математичним моделюванням. Досвiд керування написанням дослідницьких робiт у школі та врахування психологічних вікових особливостей школярів свiдчить про те, що роботи є особливо вдалими і мають позитивні результати, коли вчитель починає працювати з учнем уже з 5-го класу. Спочатку це можуть бути невеликі дослідження типу “Математика навколо нас”, “Відсотки в моїй сім’ї”, “Математика в прислів’ях”, “Енергозберігаючі технології в школі” тощо, результати яких презентуються та обговорюються на шкільних, міських, районних наукових конференціях. Така діяльність формує в учнів навички пошукової роботи, уміння обробляти отримані дані, узагальнювати і систематизувати, виховує самостійність, впевненість у собі, розкутість, уміння відстоювати власну точку зору. У подальшому робота вчителя зводиться до складання сумісно з учнями розширеного плану наукової роботи, який у процесі написання може уточнюватися та змінюватися, і контролю результату. Також корисно давати школярам додаткову літературу та настанови щодо пошуку інформації в інших джерелах (бібліотеці, Інтернеті тощо).

 Використання методу проектів, який орієнтований на самостійну діяльність учнів (індивідуальну, парну, групову) у відведений для цього час (від декількох хвилин уроку до декількох тижнів, а іноді й місяців), дозволяє узагальнити та систематизувати знання учнів про математичне моделювання на кожному з етапів навчання.

 Проектна технологія передбачає наявність проблеми, що вимагає інтегрованих знань і дослідницького пошуку її розв’язання. Результати запланованої діяльності повинні мати теоретичну, практичну та пізнавальну значущість. Дуже важливою також є структуризація змістовної частини проекту із зазначенням результатів, яких потрібно досягти на кожному етапі. Необхідною складовою методики здійснення проектної діяльності є складання загальної моделі, що розглядається як умовний образ, схема, шлях до результату проекту.

Застосування методу проектів формує:

•     загальнонавчальні вміння;
•     дослідницькі вміння: самостійно знаходити потрібні відомості, кілька варіантів вирішення проблеми, висувати гіпотези, встановлювати причинно-наслідкові зв'язки;
•     уміння та навички роботи у колективі: колективне планування, взаємодопомога в групі при вирішенні спільних завдань, навички ділового партнерського спілкування, вміння знаходити і виправляти помилки у роботі інших учасників групи;
•     менеджерські вміння та навички: проектування результату, планування діяльності та витрат часу, прийняття рішень і прогнозування їх результатів, аналіз власної діяльності;
•     комунікативні вміння: вступати в діалог, ставити запитання, вести дискусію, відстоювати власну точку зору, знаходити компроміс;
•     презентаційні вміння і навички: навички монологічного мовлення, вміння впевнено тримати себе під час виступу, артистичні вміння, вміння використовувати різні засоби наочності при виступі.

 Використовувати розроблені проекти можна як на уроках (“Системи числення” (5 клас), “У світі чотирикутників” (8 клас), “Многогранники навколо нас” (9 клас) тощо), так і під час проведення позакласних заходів (“Цікаві числа”, “Координатна площина очима художника”, “Геометрія в зимових олімпійських видах спорту”, “Планування міського парку”, “Геометрія танцю” тощо).

 Загалом, метод проектів якнайкраще відображає застосування математичного моделювання незалежно від теми дослідження та типу проекту, оскільки і процес виконання проекту, і його результат – це завжди певна модель. 

 Таким чином, вивчення за наведеною вище методикою методам математичного моделювання дає можливість розширити світогляд учнів; сприяє розвитку абстрактно-логічного мислення: лаконiчностi мови, вмiння вдало використовувати символiку, правильно застосовувати математичну термiнологiю, робити висновки та узагальнення, обґрунтовувати свої думки; забезпечує активізацію пізнавального інтересу до вивчення предмету та ефективність навчання.

 Отже, по закінченню вивчення курсів алгебри та геометрії у 9 класі можна очікувати, що в учнів будуть сформовані:

• поняття математичного моделювання, математичної моделі, її видів, етапів побудови;
• розширені уявлення про алгебраїчні вирази, рівняння, нерівності та їх системи, функції та їх графіки, планіметричні фігури як математичні моделі;
• навички побудови знако-символьних, образних моделей для доведення теорем та розв’язування прикладних задач;
• навички застосування методів математичного моделювання до доведення теорем, розв’язування задач та розробки і виконання проектів.

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 

 Одним із основних напрямків сучасної освіти є формування практично компетентної особистості, яка володіла б уміннями моделювати реальні процеси та явища, зокрема економічно-фінансові, аналізувати і порівнювати дані, прораховувати ризики, інтерпретувати результати, працювати зі знако-символьним представленням інформації і т.п. Тому формування в учнів знань, умінь і навичок математичного моделювання є одним із першочергових завдань школи. Реалізувати його можна, насамперед, у процесі навчання предметів політехнічного циклу (математики, фізики, хімії, біології, географії), а також інших предметів (трудового навчання, малювання і т.д.).

 Проведений аналіз стану розв’язання досліджуваної проблеми в науково-методичній, психолого-педагогічній, математичній літературі та рівень її практичної реалізації в навчанні математики у школі дав змогу стверджувати, що скорочення навчальних годин на вивчення математики, переважання традиційних форм роботи з учнями, незначна кількість завдань прикладного характеру у діючих підручниках з математики, зниження інтересу школярів до навчання в цілому не сприяють формуванню в учнів знань, умінь та навичок математичного моделювання. Під час розв’язування прикладних задач школярі найчастіше спрямовують свої зусилля на відшукання готової математичної моделі, а її прикладна спрямованість чи життєва інтерпретація залишаються поза увагою. Тому розробка ефективних методичних рекомендацій з формування умінь математичного моделювання в учнів 7–9 класів у процесі навчання геометрії та більш детальна розробка системи пропедевтичного навчання математичного моделювання дозволяють вирішити вище зазначені проблеми.

 Виокремлення математичного моделювання як самостійної змістової лінії шкільного курсу математики вимагає особливого підходу, оскільки зосередження його як окремої теми значно обмежує навчальний потенціал. Формування уявлення про математичне моделювання більшою мірою має супроводжувати вивчення більшості тем шкільного курсу математики, зокрема бути задіяним при формуванні понять, доведенні теорем, розв’язуванні задач.

 Для набуття учнями вмінь застосовувати методи математичного моделювання його навчання має бути наскрізним і організованим за такими етапами:

• пропедевтичний (5–6 класи) передбачає формування уявлень про математичну модель, її види, деякі властивості; уміння будувати математичну модель до задачі або складати задачу за даною математичною моделлю;

• початковий (7–8 класи) передбачає формування поняття про математичну модель, її види та етапи математичного моделювання; уміння будувати або добирати доцільні математичні моделі до задачі;
• основний (9 клас) передбачає узагальнення знань про математичну модель, її види та етапи математичного моделювання; формування уміння використовувати інформаційно-комунікаційні технології при створенні та дослідженні математичної моделі, представляти чисельні результати за допомогою наближених обчислень;
• дослідницький передбачає більш глибоке вивчення математичного моделювання на гуртках, факультативах і написання наукових робіт в системі діяльності Малої академії наук.

 Оволодіння методами математичного моделювання передбачає формування в учнів знань, умінь і навичок на основі спрощеної, адаптованої до розуміння школярів, схеми діяльності математичного моделювання, яка включає три етапи:

I етап. Побудова математичної моделі (формалізація).

II етап. Розв’язування задачі в межах математичної моделі (дослідження або аналіз моделі).

III етап. Інтерпретація одержаного розв’язку (синтез результатів).

 Стосовно методів, прийомів і форм організації навчальної діяльності школярів, то дослідження психолого-педагогічної літератури показало, що найбільш доцільним буде застосування активних методів, які б для молодших підлітків були спрямовані на стимулювання і підтримку інтересу до предмету; для середнього підліткового віку – на практичне застосування знань; для старших підлітків – на наукові засади предмету.

 Результати експериментальної перевірки підтверджують ефективність розробленої методики формування знань, умінь і навичок математичного моделювання в учнів основної школи в процесі навчання геометрії та доводять, що дотримання запропонованої методики сприяє:

• свідомому оволодінню учнями математичним моделюванням як універсальним методом навчального пізнання навколишнього середовища;
• підвищенню рівня розвитку творчих здібностей школярів;
• активізації пізнавального інтересу до вивчення предмету та ефективності навчання.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Волчаста М.М. Наступність у вивченні геометричного матеріалу в початковій та основній школі. – Дис. … канд.пед.наук. – К., 2003. – 235 с.
2. Гібалова Н.В. Методична система навчання учнів 5 – 6 класів елементів геометрії. – Дис. … канд..пед.наук. – К., 2000. – 237 с.
3. Обойщикова И.Г. Обучение моделированию учащихся 5 – 6 классов при изучении математики. – Дисс. … канд. пед. наук – Пенза, 2002 – 167 с.
4. Панченко Л.Л. Формування вмінь математичного моделювання в процесі навчання майбутніх вчителів математики: Дис…канд. пед. наук:13.00.02./ Нац. пед. ун-т імені М.П.Драгоманова. – К., 2006. – 260 с.
5. Петерсон Л.Г. Моделирование как средство формирования представлений о понятии функции в 4 – 6 классах средней школы. – Дисс. … канд. пед. наук – М., 1984. – 201 с.
6. Швець В.О., Філімонова М.О. Еволюція математичного моделювання як методу пізнання і навчання // Математика в школі. – 2010. – №4. – С. 22 – 25.
7. Філімонова М.О. Елементи математичного моделювання у процесі вивчення геометричного матеріалу в 5 – 6 класах / М.О. Філімонова,       В.О.Швець // Science and Education a New Dimension. Pedagogy and Psychology. – Budapest, 2013. – №5. – С. 149–152.
8. Філімонова М.О., Швець В.О. Математичне моделювання в курсі математики основної школи: зміст і вимоги до підготовки учнів// Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. – Вип. 34. – Донецьк: Вид-во ДонНу, 2010. – С. 72 – 76.
9. Філімонова М.О., Швець В.О. Психолого-педагогічні особливості навчання підлітків методу математичного моделювання // Математика в школі. – 2010. – №10. – С. 21 – 25.
10.  Филимонова М.А. Пути формирования у учащихся основной школы навыков математического моделирования / М.А. Филимонова, В.А. Швец// Матэматика. – 2013. – №6. – с. 59 – 64.
11. Филимонова М.А. Формы организации обучения учащихся основной школы методу математического моделирования / М.А.Филимонова, В.А.Швец // Материалы Международной научной конференции “Математическое образование: современное состояние и перспективы (к 95-летию со дня рождения профессора А. А. Столяра)”, 19—20 февраля 2014 г.— Могилев: МГУ имени А. А. Кулешова, 2014. – с. 303 – 305.
12. Швець В.О. Математичне моделювання як змістова лінія шкільного курсу математики // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. – Вип. 32. – Донецьк: Вид-во ДонНу, 2009. – С. 16 – 24.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТКИ

Добірка прикладних задач для учнів 5 – 6 класів

 

1. Відстань від дому до школи у 6 разів більша, ніж від школи до магазину. Визначте довжину шляху від дому до школи, якщо відстань від дому до магазину 490 м і школа розташована по дорозі до магазину?

Відповідь: 420 м

2. Уздовж бігової доріжки рівномірно розставлено стовпчики. Старт було дано від першого стовпчика. Через 12 хв Сергійко знаходився біля четвертого стовпчика. Через скільки хвилин від початку старту. Сергійко буде біля сьомого стовпчика, якщо його швидкість є сталою?

Відповідь: 24 хв

3. Відстань від Харкова до Києва дорівнює 483 км. Вона на 294 км більша, ніж відстань від Києва до Черкас і на 142 км більша за відстань від Черкас до Вінниці. Яку відстань подолав турист маршрутом Харків – Київ – Черкаси – Вінниця?

Відповідь:1013 км

4. Кімната у формі прямокутника має розміри 3 м × 4 м. Скільки метрів плінтуса потрібно купити для цієї кімнати?

Відповідь:14 м

5. Садок має форму прямокутника зі сторонами 6 м і 10 м. Чи вистачить 30 м паркану для того, щоб його огородити, якщо ворота та хвіртка мають сумарну довжину 2 м?

Відповідь: вистачить.

6. На уроці трудового навчання Марійка отримала завдання пошити трикутну хустинку розмірами 50 см, 50 см і 75 см. Дівчинка вирішила оздобити хустинку мереживом. Скільки їй треба купити мережива, щоб обшити хустинку?

Відповідь: 175 см

7. Довжина прямокутного поля дорівнює 850 м, а ширина — 600 м. Знайдіть площу поля і запишіть її в гектарах і арах.

Відповідь: 51 га, 5100 ар

8. Чи вистачить 5 т гороху, щоб засіяти ним поле, що має форму прямокутника зі сторонами 500 м і 400 м, якщо на 1 га землі треба висіяти 260 кг гороху?

Відповідь: не вистачить.

9. Ящик, який має форму прямокутного паралелепіпеда з вимірами 32 см,20 см і 12 см заповнили кубиками з ребром 4 см. Скільки кубиків помістилося в ящику?

Відповідь:120 кубиків

10.          Батько вирішив обкласти кахлем стіну кухні, довжина якої дорівнює 6 м, а висота – 3 м. Чи вистачить йому 5 ящиків кахлю, якщо одна плитка має форму квадрата зі стороною 15 см, а в один ящик уміщується 160 плиток?

Відповідь: вистачить

11.          Скільки треба метрів дроту, щоб виготовити каркас прямокутного паралелепіпеда з вимірами 5 м, 6 м і 8 м?

Відповідь:76 м

12.          Аркуш паперу має форму прямокутника розміром 210 мм × 297 мм. Чи вистачить одного аркуша, щоб обклеїти куб із ребром 6 см?

Відповідь: вистачить

13.          Довжина ящика дорівнює 45 см, ширина — на 15 см менша, а висота – на 5 см більша від ширини та довжини разом. Знайдіть об’єм ящика.

Відповідь: 108000 см³

14.          Довжина басейну 44 дм, ширина на 18 дм менша, а глибина дорівнює різниці довжини і ширини. Знайдіть об’єм води, якою можна заповнити весь басейн.

Відповідь: 20 592 л

15.          Довжина акваріума 12 дм, ширина удвічі менша від довжини, а висота на 5 дм менша від довжини. Знайдіть об’єм акваріума.

Відповідь: 504 л

16.          Щоб витягти відро води, треба ручку коловорота криниці повернути        15 разів. Знайдіть глибину криниці, якщо діаметр барабана дорівнює 26 см.

Відповідь:≈ 12, 246 м

17.          Діаметр велосипедного колеса дорівнює 8 дм. Скільки обертів зробить колесо, якщо велосипед проїде 1км?

Відповідь: 398 обертів.

18.          Діаметр колеса тепловоза дорівнює 80 см. За 2 хв колесо робить             800 обертів. Яка швидкість тепловоза в кілометрах за годину? Результат округліть до десятих.

Відповідь:60,3 км/год

19.          Яка клумба для квітів має більшу площу: та, що має форму квадрата зі стороною 4 м, чи та, що має форму круга з діаметром 4 м?

Відповідь:та, що має форму квадрата зі стороною 4 м

20.          Під час прогулянки Тарасик і Петрик пройшли від свого будинку спочатку 200 м прямо вулицею, на якій стоїть їхній будинок. Потім повернули ліворуч під прямим кутом і пройшли ще 200 м, а потім повернули праворуч під прямим кутом і пройшли ще 200 м. Визначте, на якій вулиці зараз перебувають хлопці: тій, що перпендикулярна до вулиці, на якій вони мешкають, чи тій, що паралельна їй?

Відповідь: на тій, що паралельна до вулиці, на якій мешкають хлопці.

 

Добірка задач до змістової лінії “Геометричні величини”

 

1.     Із двох пунктів А і В вийшли в пункт М по прямолінійних маршрутах двоє зв’язкових. Відстань АМ, пройдена першим зв’язковим, становить 4 км, а відстаньВМ, пройдена другим зв’язковим, – 6 км. Якою може бути відстань АВ?

Відповідь: ≤10 км

2.     Вздовж двох сторін алеї на відстані 3 м один від одного необхідно посадити дерева. Скільки дерев слід замовити для садівлі, якщо довжина алеї 210 м? (Перше та останнє дерево саджатимуться на кінцях алеї.)

Відповідь: 142 дерева.

3.     Автобус виїхав із пункту К в пункт М прямолінійним шляхом. Проїжджаючи повз стовп 120-го км, водій зауважив, що залишилося їхати втричі більше, ніж проїхали, а проїжджаючи повз стовп 80-го км, – що залишилося їхати втричі менше, ніж проїхали. На якому кілометрі розміщений пункт М?

Відповідь: на 60-му кілометрі.

4.     Знайдіть кут між стрілками годинника, якщо вони показують 15 год; 18 год 15 хв; 9 год; 9 год 15 хв.

Відповідь: 90˚; 97˚30ˊ; 90˚; 172˚30ˊ.

5.     Скільки найбільше кругів з діаметром 50 см можна вирізати з бляшаного листа прямокутної форми розмірами 140 см × 205 см? Яка частина матеріалу використовується при цьому?

Відповідь: 11 кругів; ≈ 75,2%.

6.     Барабан лебідки має діаметр 530 мм і довжину 727 мм. За час роботи на барабан намотується 225 м тросу з діаметром 17 мм. У скільки шарів намотується трос?

Відповідь: У три шари.

7.     Криницю циліндричної форми, діаметр якої 135 см, а глибина 380 см, потрібно викласти цеглою. Скільки штук цегли для цього необхідно, якщо розміри цеглини 25 см × 12 см × 6,5 см?

Відповідь: 826 штук.

8.     Пластинка має форму трикутника зі сторонами 25 см, 34 см і 39 см. З яким найбільшим радіусом можна вирізати круг із цієї пластинки?

Відповідь: 8,5 см.

9.     Поле має форму паралелограма, основа якого 500 м, а висота 180 м. Через це поле під прямим кутом до основи проходить шосейна дорога шириною 12 м. Визначте величину посівної площі поля.

Відповідь: 8 га.

10. Основа постаменту пам’ятника має форму квадрата зі стороною 6 м. Навколо пам’ятника розміщена алея шириною 2 м. Знайдіть площу алеї.

Відповідь: 64 м².

11. Поштукатурена стіна довжиною 8,25 м і висотою 4,32 м має три вікна розміром 2,2 м × 1,2 м кожне. Знайдіть площу тієї частини стіни, яка покрита штукатуркою.

Відповідь: 27,72 м².

12. Сад, в якому дерева посаджені в шахматному порядку, складається із          32 рядів, по 45 дерев у кожному. Сусідні дерева одного ряду розміщені на відстані 6 м, а сусідні дерева різних рядів – на відстані 8,54 м. Від паркану, яким огороджено сад, крайні дерева віддалені на 3 м. Знайдіть площу саду.

Відповідь: ≈ 7,3 га.

13. Прямокутна клумба для квітів має площу 216 м². Вздовж довших сторін клумби необхідно прокласти доріжки шириною 2 м, вздовж коротших – шириною 3 м. Які мають бути розміри ділянки (клумби разом з доріжками), щоб площа доріжок була найменшою?

Відповідь: 24 м × 16 м.

14. Петренко, вирішивши викласти підлогу у квадратній кухні площею 7,29 м² квадратним різнокольоровим кахлем, купив такий набір: 1 кахель зі стороною 120 см, 3 кахлі зі стороною 90 см, 9 кахлів зі стороною 60 см і 2 кахлі зі стороною 30 см. Василенко, власник такої ж кухні, придбав на 1 кахель більше зі стороною 120 см, на 1 кахель менше зі стороною 90 см і на 1 кахель менше зі стороною 60 см. Хто з них вчинив раціональніше? Кахлі розрізати не можна.

Відповідь: Раціональніше вчинив Петренко.

15. Повітря тисне із силою 10,3 Н на кожен квадратний сантиметр. Знайдіть силу, з якою повітря тисне на трикутний майданчик, основа якого – 0,13 м, а висота – 0,18 м.

Відповідь:  ≈ 200 Н.

16. Із прямокутного бляшаного листа довжиною 40 см та шириною 35 см вирізали для лійки частину, що має форму трапеції з основами, рівними 40 см та 12 см, і висотою 20 см. Знайдіть площу решток листа.

Відповідь: 980 см².

17. Із листа фанери розміром 220 см × 80 см необхідно вирізати для ящиків рівнобічні трапеції з основами 30 см і 10 см та гострим кутом 45˚, причому зробити креслення слід найраціональнішим способом. Скільки таких трапецій можна вирізати з цього листа?

Відповідь: 83 трапеції.

18. Підлогу прямокутного фойє театру, розмір якої 14,6 м × 8,4 м, необхідно викласти керамічним кахлем двох різних кольорів (порівну кожного кольору). Скільки слід замовити кахлю кожного кольору, якщо він має форму правильного шестикутника зі стороною 10 см?

Відповідь:2359 штук.

19. З бляшаного листа, який має форму прямокутної трапеції з основами 30 см і 20 см та висотою 20 см, вирізано круг найбільшого діаметру. Який відсоток складають відходи?

Відповідь: 37,2 %.

20. Обчисліть площу вікна, що має форму прямокутника, який закінчується зверху сегментом у 60˚. Висота вікна відраховується від середини дуги сегменту до основи та рівна 2,4 м, ширина – 1,6 м.

Відповідь: ≈ 3,7 м².

 

Добірка задач до змістової лінії “Геометричні фігури”

 

1.     Із металевого дробу треба зробити деталь, яка мала б форму рівнобедреного трикутника. Одна зі сторін трикутника повинна мати довжину 25 см, а друга    10 см. Якою має бути довжина дроту, щоб можна було це виконати?

Відповідь: 60 см.

2.     Столяру необхідно виготовити деталь трикутної форми. Скільки розмірів і які він повинен знати, щоб виконати замовлення, якщо деталь має форму:         а) прямокутного трикутника; б) рівностороннього трикутника?

Відповідь: а) два; б) один.

3.     Кут між кроквами металевого даху, як правило, дорівнює 120˚. Знайдіть довжину крокви, якщо її верхній кінець віддалений від основи даху на 2,5 м.

Відповідь: 5 м.

4.     Визначте кут підйому залізничної колії, якщо на довжині 100 м висота підйому дорівнює 4 м.

Відповідь: .

5.     На залізниці необхідно побудувати станцію з таким розрахунком, щоб вона знаходилася на однакових відстанях від двох населених пунктів. Де повинна розміщуватися станція? У якому випадку таку станцію побудувати неможливо?

Відповідь: Слід побудувати серединний перпендикуляр до відрізка, що сполучає дві точки – населені пункти, і знайти точку його перетину із прямою, що є зображенням залізниці. Задача не має розв’язку, якщо точки, що зображають населені пункти, знаходяться на одному перпендикулярі до прямої, що зображає залізницю, але на різних відстанях від неї.

6.     У прямокутній пластині слід зробити круглий отвір на однаковій відстані від її вершин. Як знайти центр цього отвору?

Відповідь: Знайти точку перетину діагоналей.

7.     Фруктовий сад має форму прямокутника, сторони якого відносяться як 16:11, причому його ширина менша від довжини на 250 м. Скільки часу необхідно сторожу, щоб обійти увесь сад вздовж паркану, йдучи зі швидкістю   4 км/год?

Відповідь: 40,5 хв.

8.     Столяру необхідно виготовити підставку у формі чотирикутника. Скільки і які розміри він повинен знати, щоб виконати замовлення? Що повинен виміряти столяр, якщо підставка має форму: а) паралелограма;                            б) прямокутника; в) ромба; г) квадрата?

Відповідь: Необхідно мати п’ять розмірів: чотири сторони і кут; три сторони і два кути; дві сторони і три кути. а) дві суміжні сторони та кут між ними; б) дві суміжні сторони; в) сторону і один з кутів; г) сторону.

9.     Між двома телеграфними стовпами на одній з ними прямій і на однаковій відстані від них розміщено третій телеграфний стовп. На якій відстані від дороги, знаходиться цей стовп, якщо два інші віддалені від неї на 32 м і 58 м?

Відповідь: 45 м.

10. Земельну ділянку, що має форму трапеції, віддали під спортивний майданчик. Які розміри повинен знати землемір, щоб накреслити план цієї ділянки?

Відповідь: три сторони і один кут.

11. Під парк відведено ділянку землі, яка має форму рівнобедреної трапеції, одна з основ якої на 50 м більша кожної із решти сторін, а середня лінія дорівнює 90 м. Навколо парку розміщено алею шириною 2 м. По обидва боки алеї потрібно посадити дерева на відстані 3 м одне від одного. Скільки потрібно замовити саджанців?

Відповідь: 212 саджанців.

12. Ділянка, зайнята фруктовим садом, має форму трапеції. Дерева розміщені п’ятьма паралельними між собою рядами, однаково віддаленими один від одного. У всіх рядах відстані між сусідніми деревами однакові. У крайніх рядах кількість дерев 18 та 26 відповідно. Скільки дерев у кожному із решти рядів?

Відповідь: 20, 22, 24 дерева відповідно.

13. Сейсмічною станцією зафіксовані сильні підземні поштовхи на відстані       75 км від станції під кутом 30^о до поверхні землі. Між станцією і вулканом 48 км. Визначити глибину осередку (гіпоцентру) землетрусу.

Відповідь: км.

14. Із гвинтокрила, що знаходиться над дорогою, помічено колону машин. Початок колони видно під кутом 75°, а її кінець – під кутом 70°. Знайти довжину колони, якщо гвинтокрил знаходиться на висоті 1650 м.

Відповідь:1042 м.

15. Лісник спостерігає за пожежею із вишки, побудованої на високому пагорбі. Висота пагорба 726 м, а висота вишки – 24 м. На якій відстані від пункту спостереження виникла пожежа, якщо лісник помітив вогонь під кутом 7˚ до горизонту?

Відповідь:  ≈ 6153 м.

16. Літак наближається до аеропорту, знаходячись на висоті 7000 км. Пілот має розпорядження здійснювати зниження для посадки під постійним кутом 6˚. На якій відстані (з точністю до 1 км) від посадкової смуги він повинен розпочати зниження?

Відповідь: ≈ 67 км.

17. Драбина довжиною 12,5 м приставлена до стіни так, що відстань від її нижнього кінця до стіни дорівнює 3,5 м. На якій висоті від землі впирається у стіну верхній кінець драбини?

Відповідь: 12 м.

18. Від пристані одночасно відпливли два теплоходи: один на південь зі швидкістю 16 морських миль за годину, а другий на захід зі швидкістю             12 морських миль за годину. Яка відстань буде між теплоходами через 2,5 год, якщо 1 морська миля ≈ 1,85 км?

Відповідь: ≈ 92,5 км.

19. Чи можливо скласти паркет із правильних десятикутників і п’ятикутників і чому?

Відповідь: Неможливо.

20. Лісова галявина має форму ромба. У якій точці галявини слід знаходитися, щоб одночасно почути відлуння свого вигуку від усіх сторін лісу?

Відповідь: У точці перетину діагоналей ромба.

 

Добірка задач до тем “Декартові координати на площині”

та “Вектори на площині”

 

1.     Знайдіть координати центра шківа, який треба розмістити рівновіддалено від двох взаємно перпендикулярних планок і від шарніра, який віддалений від планок на 3 одиниці і на 6 одиниць.

Відповідь: О (15; 15) і О (3; 3).

2.     Знайдіть місце розміщення центра шківа з радіусом 5 дм, щоб він проходив через точку, яка віддалена від двох взаємно перпендикулярних стержнів на 2 дм і 4 дм, а його центр знаходився на одному із заданих стержнів і дотикався до другого.

Відповідь: О (5; 0).

3.     На відстані 1 км від газопроводу треба побудувати газорозподільну станцію, з якої газ по трубах надходитиме до населених пунктів А і В, віддалених від газопроводу відповідно на 4 км і на 9 км. Відстань між населеними пунктами   13 км. В якому місці треба побудувати газорозподільну станцію, щоб відстань від неї до пунктів А і В була однаковою? Визначте довжину газопровідних труб, прокладених до населених пунктів А і В.

Відповідь: Газорозподільна станція знаходиться у точці з координатами (8,3; 1). Довжина газопровідних труб дорівнює приблизно 8,8 км.

4.     Обчислити роботу, яку виконує сила 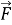= (6; 2), якщо її точка прикладання, рухаючись прямолінійно, переміщається з положення А (-1; 3), в положення     В (3; 4).

Відповідь: 26 Дж.

5.     Знайти потужність, яку розвиває сила рівна 5 Н, що діє на швидкість у       3,5 м/с, якщо кут між ними 45º.

Відповідь: ≈ 12,4 Вт.

6.     На одну точку діють три сили F₁ = 10 H, F₂ = 10 H, F₃ = 20 H. Ці сили розміщені в одній площині, кожні дві сусідні сили утворюють кут 120º. Визначте напрямок та величину рівнодіючої сили.

Відповідь: напрямок рівнодіючої сили відповідаю напрямку сили F₃, а її величина рівна 10 Н.

7.     Під яким кутом треба направити човен до берега, щоб перебратися на другий берег річки найкоротшим шляхом, коли відомо, що власна швидкість човна 50 м/хв, швидкість течії 25 м/хв., а ширина річки 250 м? Скільки часу триватиме переправа?

Відповідь: під кутом 30º; ≈ 5,77 хв.

8.     Яку силу слід прикласти під кутом 31º до напрямку руху, щоб на шляху, довжиною 100 м, вона виконала роботу, рівну 1400 Дж?

Відповідь: ≈ 16,3 Н.

9.     Вантаж масою 3 т підвішений на двох канатах, симетрично розміщених відносно вертикалі, кут між якими дорівнює 60º. Знайдіть сили натягів канатів.

Відповідь:

10. На вантаж, що ковзає по плоскій горизонтальній поверхні, діє сила 200 Н, напрямлена під кутом 60º до горизонту. Яку роботу виконує сила під час переміщення на 5 м, якщо вантаж рухається прямолінійно і рівномірно?

Відповідь: 500 Дж.

11. Сили 7,25 Н і 10,3 Н діють на одну і ту ж точку тіла перпендикулярно одна до одної. Знайдіть рівнодіючу цих сил і кути, які вона утворює з ними.

Відповідь: ≈ 12,6 Н; ≈ 35º; ≈ 55º.

12. Рівнодіюча двох взаємно перпендикулярних сил, прикладених до однієї точки, утворює із однією із складових сил, яка дорівнює 8 Н, кут 35º. Знайдіть іншу складову силу.

Відповідь: ≈ 5,6 Н.

13. До точки прикладена сила 18,3 Н. Відома одна її складова, рівна 12,8 Н і кут 37º між даною силою і відомою складовою. Знайдіть іншу складову.

Відповідь: ≈ 11,2 Н