Методичний посібник " Метод інтервалів"
Метод інтервалів заснований на властивості чергування знаків функції: функція змінює знак при переході через нулі функції та точки, в яких функція не існує. На проміжках, на які область визначення розбивається цими точками, знак функції не змінюється.
Алгоритм методу інтервалів:
1 .в правій частині нерівності залишаємо нуль; 2.перетворюємо ліву частину нерівності так, щоб кожний множник чисельника і знаменника мав додатній старший коефіцієнт; 3.знаходимо ОДЗ нерівності; 4.знаходимо нулі функції, яка знаходиться в лівій частині нерівності; 5.на координатнy прямy наносимо ОДЗ, 6. позначаємо нулі функції і показуємо утворені проміжки; 7.визначаємо знак функції на кожному проміжку. Якщо старші коефіцієнти всіх множників додатні і кожна границя утворених проміжків повторюється один раз, сміливо в крайньому праворуч проміжку ставимо знак “+”, або будь-яке число з кожного проміжку підставляємо в ліву частину нерівності і дивимося на знак отриманого числа; 8.обираємо проміжки згідно знаку нерівності і записуємо відповідь.
Розглянемо приклади рішення дробово-раціональних нерівностей стандартного вигляду; нерівностей, в яких нулі, або точки в яких функція не існує повторюються парне число разів; нерівності, в яких отримані ірраціональні числа треба порівняти без калькулятора і наближених обчислень ; нерівності зі знаком модуля.
1 приклад . Розв’язати нерівність. 
; 
-
ОДЗ: х
-1; х
Функція у =
нулів не має, так як 
+9 > 0. Нанесемо на координатну пряму тільки точки, в яких функція не існує. В крайньому справа проміжку функція буде мати додатній знак, бо в кожному множнику старший коефіцієнт додатній. А далі знаки чергуються.
+ - +
-2 -1
Відповідно знаку нерівності (
0) записуємо відповідь.
Відповідь: х є
U
2 приклад. Розв’язати нерівність.
;
ОДЗ: x
Нулі функції: 
x–2 = 0; x=
. Цей нуль функції парної кратності, тому зручно поставити індекс 2, цим показуємо, що функція два рази проходе через точку
х=2, і свій знак не змінює.
Відмічаємо числа -1; -2; 2 на координатній прямій і розставляємо знаки функції на отриманих проміжках. Так як в усіх множниках старший коефіцієнт додатній, то в крайньому справа проміжку ставимо знак “+”, далі знак повторюється, а потім змінюється на протилежний.
+ - + +
Відповідно знаку нерівності (
записуємо відповідь, враховуючи, що знак нерівності не строгий і число 2 входить в множину рішень нерівності.
Відповідь: x є 
.
3 приклад. Розв’язати нерівність.
.
ОДЗ: x - 1
; x
.
Нулі функції: ( 
- x – 6)
=0;
- x – 6 = 0; x - 1= 0;
х = - 2; x = 3; x = 1.
Не розглядаємо - +
-2 1 3
Відповідь: x
U
).
4 приклад. Розв’язати нерівність. Отримані шляхом рішення ірраціональні числа порівняти без калькулятора і наближених обчислень.
- 1 > 0; 
> 0; 
> 0; 
ОДЗ: - 6 x - 12
. (Використали формулу
для зведених квадратних рівнянь з парним другим коефіцієнтом).
Нулі функції: 
;
= 2
;
.
Треба порівняти числа 3 -
та 2 - 
без калькулятора, щоб правильно розташувати їх на координатній прямій. Використаємо властивості квадратичної функції y=
-4x-7.
+ +
2-
- 2+
На проміжку (2-
; 2 +
) вона має від’ємний знак. Припустимо, що число 
> 2 - 
тоді значення функції у =
в точці (3 - ) повинно бути від’ємним. Перевіримо це, підставивши
х =3 -
в формулу у =
- 4х - 7:
у=
- 4( 3-) – 7 = 9 - 6
+ 21 - 12+4 -7= =
-
>0, значить наше припущення помилкове і 3 - 
2- .
+ - + - +
3-
2- 2+
Враховуємо знак нерівності (<0) і записуємо відповідь.
Відпо6відь: x є (3-; 2-) U (2+; 3+).
5 приклад. Розв’язати нерівність зі знаком модуля.
Розглянемо два випадки:
1. x
Тоді
або
ОДЗ: x
Нулі функції: x+1=0; x= -1.
Враховуючи, що х
знайдемо множину рішень на координатній прямій.
Не розглядаємо - +
-1 0 2
х є (2 ;+
.
2. х 
Тоді 
ОДЗ: x
Нулі функції: 13x+1 = 0; x = -
.
Враховуємо,що х < 0 і знак нерівності (
).
+ - + не розглядаємо
-2 - 
0
х є (-2; 
].
Знайдемо спільну відповідь даної нерівності - це об’єднання множин рішень двох попередніх нерівностей.
Відповідь: x
.
6 приклад. Розв’язати нерівність зі знаком модуля.
Використовуючи означення модуля, маємо подвійну нерівність -1 <
< 1,
або систему двох нерівностей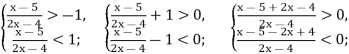 
Спростимо першу нерівність.
> 0;
ОДЗ: x
нулі функції: x - 3 = 0; х = 3.
Спростимо другу нерівність.
ОДЗ: x нулі функції: x+1=0; х = -1.
Зобразимо множину рішень кожної нерівності на координатних прямих:
+ - +
2 3
+ - +
-1 2
З малюнку бачимо, що розв’язком системи нерівностей буде об’єднання двох проміжків.
Відповідь: x є (
(3;+
).
Задачи для самостійного рішення.
Розв’яжіть нерівності методом інтервалів.
1.
>
; 2. 
3. 
4. 
;
5.
Розв’яжіть нерівності методом інтервалів.
6. 
7. 
8. 
Розв’яжіть нерівності зі знаком модуля.
9. 
10. 
11. 
12. 
13. 
14.
Розв’язати нерівність. Отримані ірраціональні числа порівняти без калькулятора та наближених обчислень.
15. 
16. 
17. 
18. 
> 0;
19. 
20. 
21. 
Краснолиманській ліцей
Розв’язування добово-раціональних нерівностей методом інтервалів
Склала Капшук Т.В.
2014рік
про публікацію авторської розробки
Додати розробку