Вычисление определенного интеграла. Формула Ньютона-Лейбница.
Вычисление определенного интеграла. Формула Ньютона-Лейбница.
Пусть в определенном интеграле ![]() нижний предел ɑ закреплен, а верхний предел b меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела.
нижний предел ɑ закреплен, а верхний предел b меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела.
Для того чтобы иметь привычные обозначения, верхний предел b обозначим через x, а чтобы не смешивать его с переменной интегрирования, последнюю обозначим через t (от обозначения переменной интегрирования значение интеграла не зависит). Получим интеграл ![]() . При постоянном ɑ этот интеграл будет представлять собой функцию верхнего предела x. Эту функцию мы обозначим через F(x):
. При постоянном ɑ этот интеграл будет представлять собой функцию верхнего предела x. Эту функцию мы обозначим через F(x):
F(x)=![]() (1)
(1)
Если f(t) - неотрицательная функция, то величина F(x) численно равна площади криволинейной трапеции aАXx.
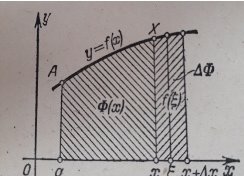
Очевидно, что эта площадь изменяется в зависимости от изменения x. Найдем производную от F(x) по x, т.е. найдем производную определенного интеграла (1) по верхнему пределу.
Теорема 1. Если f(x) – непрерывная функция и F(x)=![]() , то имеет место равенство F'(x)=f(x)
, то имеет место равенство F'(x)=f(x)
Иными словами, производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела (при условии, что подынтегральная функция непрерывная).
Доказательство. Дадим аргументу x положительное или отрицательное приращение ![]() x; тогда (учитывая одно из свойств определенного интеграла) получим:
x; тогда (учитывая одно из свойств определенного интеграла) получим:
F(x+![]() x)=
x)=![]() =
=![]() +
+![]() .
.
Приращение функции F(x) равно
![]() = F(x+
= F(x+![]() x) – F(x)=
x) – F(x)= ![]() +
+![]() -
- ![]()
т.е. ![]() =
=![]()
К последнему интегралу применим теорему о среднем значении
(свойство определенного интеграла)
![]() =f(µ)(x+
=f(µ)(x+![]() -x) = f(µ)
-x) = f(µ)![]() , где µ- заключено между x и x+
, где µ- заключено между x и x+![]()
Найдем отношение приращения функции к приращению аргумента:
![]() =
= ![]() = f(µ). Следовательно, F'(x)=
= f(µ). Следовательно, F'(x)=![]() =
=![]() .
.
Но так как µ→x при ![]() , то
, то ![]() =
=![]() , а вследствие непрерывности функции f(x):
, а вследствие непрерывности функции f(x): ![]() =f(x). Таким образом F'(x)=f(x). Теорема доказана.
=f(x). Таким образом F'(x)=f(x). Теорема доказана.
Данная теорема просто иллюстрируется геометрически (на рисунке выше): приращение ![]() f(µ)
f(µ)![]() равняется площади криволинейной трапеции с основанием
равняется площади криволинейной трапеции с основанием ![]() , а производная F'(x)=f(x) равна длине отрезка xX.
, а производная F'(x)=f(x) равна длине отрезка xX.
Замечание. Из доказанной теоремы, в частности, следует, что всякая непрерывная функция имеет первообразную. Действительно, если функция f(t) непрерывна на отрезке [a, x], то, в этом случае определенный интеграл ![]() существует, т.е. существует функция F(x)=
существует, т.е. существует функция F(x)=![]() . Но по доказанному выше она является первообразной от f(x).
. Но по доказанному выше она является первообразной от f(x).
Теорема 2. Если F(x) есть какая-либо первообразная от непрерывной функции f(x), то справедлива формула: ![]() F(b)-F(a). Эта формула называется формулой Ньютона-Лейбница.
F(b)-F(a). Эта формула называется формулой Ньютона-Лейбница.
Доказательство. Пусть F(x) есть некоторая первообразная от функции f(x). По теореме 1 функция ![]() есть также первообразная от f(x). Но две любые первообразные от данной функции отличаются на постоянное слагаемое С. Следовательно, можно написать :
есть также первообразная от f(x). Но две любые первообразные от данной функции отличаются на постоянное слагаемое С. Следовательно, можно написать : ![]() = F(x)+С.
= F(x)+С.
Это равенство при соответствующем выборе С справедливо при всех значениях x, т.е. является тождеством. Для определения постоянного С положим в этом тождестве x=a; тогда![]() = F(x)+С, или 0= F(a)+С, откуда С= -F(a). Следовательно,
= F(x)+С, или 0= F(a)+С, откуда С= -F(a). Следовательно, ![]() = F(x)-F(a). Полагая x=b, получим формулу Ньютона-Лейбница:
= F(x)-F(a). Полагая x=b, получим формулу Ньютона-Лейбница: ![]() F(b)-F(a), или заменив обозначение переменной интегрирования на x:
F(b)-F(a), или заменив обозначение переменной интегрирования на x: ![]() F(b)-F(a).
F(b)-F(a).
Отметим, что разность F(b)-F(a) не зависит от выбора первообразной F, так как все первообразные отличаются на постоянную величину, которая при вычитании все равно умножается. F(b)-F(a)= F (x)| ![]() , то формулу (2) можно переписать так:
, то формулу (2) можно переписать так: ![]() F (x)|
F (x)| ![]() = F(b)-F(a).
= F(b)-F(a).
Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции. Только с открытием этой формулы определенный интеграл смог получить то значение в математике, какое он имеет в настоящее время. Хотя с процессом, аналогичным вычислению определенного интеграла как предела интегральной суммы, были знакомы еще в древности (Архимед), однако приложения этого метода ограничивались теми простейшими случаями, когда придел интегральной суммы мог быть вычислен непосредственно. Формула Ньютона-Лейбница значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различных задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла к технике, механике, астрономии и т. д.
Примеры:
-
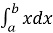 =
=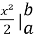 =
=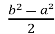 ;
;
-
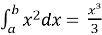 |
|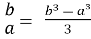 ;
;
-
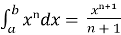 |
|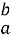 =
=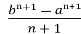 (nǂ-1);
(nǂ-1);
-
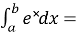 e˟|
e˟|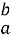 = eᵇ-eᵃ;
= eᵇ-eᵃ;
-
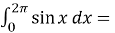 -cos x|
-cos x|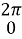 = - (cos
= - (cos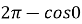 )= 0;
)= 0;
-
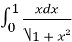 =⎷1+x²|
=⎷1+x²|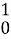 =⎷2 - 1
=⎷2 - 1

про публікацію авторської розробки
Додати розробку
