Методичний посібник: "Метод математичної індукції в шкільному курсі математики"

 

 

 

 

 

 

Займак І. І.

 

Метод математичної індукції

в шкільному курсі математики

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Займак Ірина Іванівна - учитель математики Машівського опорного навчального закладу ( ЗОШ І-ІІІ ступенів), педагогічний стаж – 35 років

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

ВСТУП……………………………………………………………………………4

РОЗДІЛ 1. Розробка уроків по темі «Метод математичної індукції»……….6

РОЗДІЛ 2. Застосування методу математичної індукції до розв’язування вправ…………………...…………………………………………………………26

2.1. Метод математичної індукції в розв’язуванні задач на підсумовування та доведення тотожностей……………………………..26

2.2. Доведення нерівностей за допомогою методу математичної індукції……………………………………………………….……………31

2.3. Задачі на подільність…………………………………………………32

2.4. Вивчення властивостей числових послідовностей……………...…35

2.5. Вивчення властивостей скінчених множин…………………..…….37

2.6. Математична індукція в геометрі……………………………..…….38

2.7. Метод математичної індукції при доведенні деяких теорем….…..41

2.8. Різні схеми застосування методу математичної індукції….……..45

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ…………………………………….51

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

Дедукція та індукція – це основні методи наукового мислення, тобто міркувань, висновків, дослідів.

У математиці, теоретичній механіці, теоретичній фізиці, математичній лінгвістиці використовується дедуктивна побудова теорії. Слово «дедукція» в перекладі на українську мову означає «виведення». Дедуктивне міркування – це міркування від загального до конкретного, тобто міркування , вихідним моментом якого є загальне міркування , а кінцевим моментом – конкретний випадок.

Але часто і в математиці, а особливо в науках, пов’язаних з експериментами, із вивченням природних явищ, спостерігається повторення будь – яких властивостей, або «конкретностей». Це повторення наводить на думку про закономірності. Загальні висновки , отримані  на підставі окремих випадків , називаються індуктивними , а сам метод таких міркувань – індуктивним методом або індукцією ( від латинського inductio- наведення).

 Індукція – це метод мислення – не може бути зведенням до простого перелічення обмеженого числа сприятливих випадків. Проста перелічильна індукція частіше приводить до помилкових , ніж до істинних узагальнень та в кращому випадку має евристичне значення наведення на більш або менш імовірні припущення. Наукові принципи індукції були розроблені понад 400 років тому англійським ученим Френсісом Беконом. Він уперше поставив перед собою проблему сформулювати принципи наукової індукції, яка «проводила б у досліді поділ на відбір та шляхом необхідних виключень й відкидань робила б необхідні висновки» .

Індукція є основним методом досліджень в експериментальних науках. Але її роль велика і в математиці, бо вона дозволяє в пошуках нового загального закону використовувати виникаючі при цьому гіпотези, відкидати невірні  та стверджувати істинні. 

Тема «метод математичної індукції» займає важливе місце в курсі математики, бо закладає основи аналітичного мислення, формує інтуїцію, розвиває увагу, уміння аналізувати, висувати наукові гіпотези та доводити їх або спростовувати . За допомогою методу математичної індукції можна розв’язати великий клас задач . На жаль, у шкільному курсі математики для загальноосвітніх класів дана тема не розглядається, а в профільних класах та класах з поглибленим вивченням математики розкрита неповністю, розглянуто не всі можливі випадки застосування даного методу.

Метою даного посібника було надати методичні рекомендації щодо вивчення даної теми на уроках алгебри в класах з поглибленим вивченням математики (9 клас), профільних класах ( 10 клас), систематизувати матеріал для проведення факультативних занять ,підготовки учнів до олімпіад, написання контрольних робіт при захисті науково - дослідницьких робіт в системі МАН України.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1

РОЗРОБКА УРОКІВ ПО ТЕМІ «МЕТОД МАТЕМАТИЧНОЇ ІНДУКЦІЇ»

Урок №1

Тема уроку. Метод математичної індукції та його застосування

Мета уроку. Формувати в учнів поняття «неповної індукції», «методу математичної індукції», навики застосування методу математичної індукції для доведення тотожностей. Розвивати логічне мислення, культуру математичного мовлення , письма, вміння готувати повідомлення , вміння вести конспект. Виховувати наполегливість, свідоме ставлення до навчання, пізнавальні інтереси учнів, розширювати кругозір .

Обладнання :  портрети Бекона, Л.Ейлера, Х.Гольдбаха, І.Виноградова, П’єра Ферма , опорна схема «метод математичної індукції», етимологічний словник

Тип уроку : вивчення нового матеріалу.

Хід уроку

І. Організаційний момент

ІІ. Мотивація пізнавальної діяльності учнів 

• За допомогою яких методів  людина пізнає світ? Думки учнів. ( Метод «мікрофон»)

Вступне слово вчителя Дедукція та індукція – це основні методи наукового мислення, тобто міркувань, висновків, дослідів.

У математиці, теоретичній механіці, теоретичній фізиці, математичній лінгвістиці використовується дедуктивна побудова теорії. Слово «дедукція» в перекладі на українську мову означає «виведення». Дедуктивне міркування – це міркування від загального до конкретного, тобто міркування , вихідним моментом якого є загальне міркування , а кінцевим моментом – конкретний випадок.

Але часто і в математиці, а особливо в науках, пов’язаних з експериментами, із вивченням природних явищ, спостерігається повторення будь – яких властивостей, або «конкретностей». Це повторення наводить на думку про закономірності. Загальні висновки , отримані  на підставі окремих випадків , називаються індуктивними , а сам метод таких міркувань – індуктивним методом або індукцією ( від латинського inductio- наведення).

 Наприклад, задовго до відкриття законів руху Землі люди зробили висновок , що Сонце вранці встає на сході, а ввечері зникає за обрієм на заході. Цей висновок є індуктивним: адже він базується лише на спостереженнях.

 Звісно за допомогою індукції не завжди можна отримати правильні висновки. Так, якщо в нашій школі серед учителів початкових класів немає чоловіків , то це не означає , що всі вчителі початкових класів – жінки.

 Індукція – це метод мислення – не може бути зведенням до простого перелічення обмеженого числа сприятливих випадків. Проста перелічильна індукція частіше приводить до помилкових , ніж до істинних узагальнень та в кращому випадку має евристичне значення наведення на більш або менш імовірні припущення. Наукові принципи індукції були розроблені понад 400 років тому англійським ученим Френсісом Беконом ( портрет). Він уперше поставив перед собою проблему сформулювати принципи наукової індукції, яка «проводила б у досліді поділ на відбір та шляхом необхідних виключень й відкидань робила б необхідні висновки» .

 Індукція є основним методом досліджень в експериментальних науках. Але її роль велика і в математиці, бо вона дозволяє в пошуках нового загального закону використовувати виникаючі при цьому гіпотези, відкидати невірні  та стверджувати істинні.  - Тема «метод математичної індукції» займає важливе місце в курсі математики, бо закладає основи аналітичного мислення, формує інтуїцію, розвиває увагу, уміння аналізувати, висувати наукові гіпотези та доводити їх або спростовувати ; за допомогою методу математичної індукції можна розв’язати великий клас задач

ІІІ .Повідомлення теми та мети уроку

На сьогоднішньому уроці ми розглянемо поняття «повної» та «неповної індукції», «методу математичної індукції», покажемо застосування даного методу для сумування та  доведення тотожностей, як одного із прикладів застосування даного методу до розв’язування математичних задач.

IV. Первинне сприймання навчального матеріалу

План вивчення нового матеріалу

1.Повна та неповна індукція.

2.Принцип математичної індукції. Метод математичної індукції.

3.Метод математичної індукції в розв’язуванні задач на підсумовування та доведення тотожностей.

Ваше завдання не просто сприймати навчальний матеріал, а ще  вести записи, вчитись складати конспект.

Повна та неповна індукції

Розповідь учителя. Найпростішим методом індуктивного міркування є повна індукція. Вона полягає в тому ,що загальне твердження доводиться поодинці, в кожному з обмеженого числа можливих випадків.

Приклад 1. Довести, що для всіх дійсних і справедливе твердження:

      

Розв’язання. Можливі чотири випадки:

Розглянемо кожен з випадків.

1) Якщо  , то і нерівність набуде такого вигляду та є істинним твердженням.

2) Якщо то і тому не більший за більше з чисел та . Але тоді

3) Якщо , то доведення нерівності аналогічне випадку 2.

4) У випадку , коли , матимемо:

і тому твердження     

                            істинне.

Отже, дана нерівність є істинною в кожному з чотирьох можливих випадків.

 Такий метод перебору скінченої кількості всіх можливих випадків називають повною індукцією.

Приклад 2. У 1742 році член Петербурзької Академії наук Х.Гольдбах у листі до Л.Ейлера висловив гіпотезу , що кожне парне число, більше від 2,можна подати як суму двох простих чисел. Ця гіпотеза досі не доведена і не спростована . Але , якщо обмежитись числами , меншими від певного числа, то таке твердження можна довести (демонстрація портретів учених)

Доведення. Доведемо, наприклад, що всяке парне число , яке задовольняє нерівність , можна представити у вигляді суми двох простих чисел. Оскільки таких простих чисел скінчене число, то це твердження можна довести методом повної індукції, розглянувши всі можливі випадки: 4=2+2, 6=3+3, 8=3+5, 10=3+7, 12=5+7, 14=3+11, 16=5+11, 18=5+13, 20=3+17, 22=5+17, 24=7+17, 26=13+13, 28=5+23, 30=7+23.

Тим самим сформульоване твердження доведене.

Суттєвий результат у цьому напрямі зробив російський математик, академік Іван Матвійович Виноградов, який довів, що будь – яке досить велике парне число є сумою чотирьох простих чисел.

Необхідно відмітити, що  іноді індуктивні міркування приводять до невірних висновків. Про це нам підготував повідомлення учень ( попередньо з учнем проговорено даний матеріал).

Повідомлення учня. Розглядаючи числа виду, французький математик ХVІІ століття П’єр Ферма , помітив, що всі числа такого виду прості. Однак  видатний математик ХVІІІ століття Леонард Ейлер знайшов, що вже при число не є простим, воно ділиться на 641.

 Наведемо приклад , що належить члену Петербурзької академії наук Л.Ейлеру. Розглянемо квадратний тричлен і обчислимо значення многочлена при дістанемо :

Легко помітити, що всі ці числа прості. Підставляючи , ми ще довго діставатимемо прості числа . Тому природно висловити гіпотезу, що значення при всіх натуральних є простими. Але ця гіпотеза є неправильною, оскільки, якщо , ми дістанемо, , тобто - складене число.

Учитель. Отже, індукція може привести як до правильних, так і неправильних висновків. Можливість неправильного висновку при індукції пов’язана з тим, що ми розглядаємо лише окремі випадки і хочемо зробити на основі цього загальний висновок. Даний метод неповної індукції можна використовувати лише для того, щоб висловити деяку правдоподібну гіпотезу, яку потім необхідно або довести або спростувати.

Для індуктивного переходу від твердження перевіреного на скінченій підмножині до аналогічного твердження для всієї нескінченої множини необхідно доведення. Але як здійснити перевірку для нескінченого числа випадків?  Такий спосіб запропонували Б.Паскаль та Я.Бернуллі. Тепер він має назву – метод математичної індукції. А базується він на принципі математичної індукції.

Принцип математичної індукції. Метод математичної індукції

 Якщо твердження , у формулюванні якого є натуральне число , істинне , коли , і зі справедливості даного твердження , коли , випливає його справедливість , коли , то твердження є істинним  для всіх .

 Цей принцип за змістом досить очевидний , приймають за одну з аксіом натуральних чисел і називають принципом математичної індукції

 Метод доведення , що ґрунтується на принципові математичної індукції, називається методом математичної індукції.

 Доведення методом математичної індукції  проводиться так. Спочатку твердження перевіряють при . Цю частину доведення називають базою індукції.  Якщо при твердження істинне, то переходять до другої частини доведення , що називають індуктивним кроком або  індуктивним переходом. У цій частині доводять справедливість твердження для , допускаючи істинність твердження , коли .

Опорна схема

1. Перевіряємо істинність твердження при
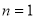
2.  Припускаємо істинність твердження при 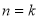та доводимо істинність твердження при .
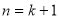3. Робимо висновок про істинність твердження для будь- яког натурального .

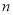Метод математичної індукції в розв’язуванні задач на підсумовування та доведення тотожностей

Вправа 1. Обчислити суму перших непарних натуральних чисел.

Розв’язання.  Будемо спостерігати як «поводиться» сума перших непарних чисел. Маємо:

 

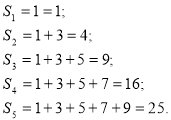
 Числа 1,4,9,16,25 є квадратами послідовних натуральних чисел.

Тепер можна зробити припущення, що для будь – якого натурального :                

Доведемо цей факт методом математичної індукції.

1). База індукції .Перевіряємо істинність твердження при .

.

2) Індуктивний перехід .Припустимо, що дане твердження істинне при , тобто твердження :   - справедливе.

 Доведемо, що дана рівність справедлива і коли , тобто є правильною рівність: 

Розглянемо ліву частину

         

Але за припущенням індукції , сума .

  Отже, вся сума дорівнює

     За принципом математичної індукції , істинність твердження доведено для будь – якого .

V. Відпрацювання навичок розв’язування вправ

Вправи розв’язуються учнями на дошці, вчитель надає допомогу, ставить навідні запитання  при виникненні труднощів.

Вправа 2. Довести, що

Доведення.  1) База індукції. Перевіряємо істинність твердження при .

2) Індуктивний перехід. Припускаємо істинність твердження при , тобто

  та  доводимо істинність твердження при .

Отже , твердження істинне при , а з його істинності при , випливає його істинність при . За принципом математичної індукції , припущення істинне при всіх натуральних .

Вправа 3. Довести, що для будь – якого натурального виконується рівність

Розв’язання. Доведемо її методом математичної індукції.

1) База індукції. Якщо , то

Дана формула справедлива при

2) Індуктивний перехід. Припустимо, що формула справедлива при , тобто і доведемо істинність при .

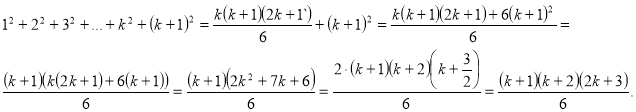 Отже , твердження істинне при , а з його істинності при , випливає його істинність при . За принципом математичної індукції , припущення істинне при всіх натуральних .

VI. Підсумок уроку.( Незакінчене речення)

На сьогоднішньому уроці я дізнався…

Цікавим для мене було те, що…

Мені хотілося б дізнатись про …

VІI. Домашнє завдання .

Вивчити теоретичний матеріал.

Вправа 1. Числа 24,44,64, 84 кратні 4. Чи можна звідси зробити висновок, що число, яке закінчується цифрою 4, кратне 4?

Вправа 2. Довести , що

Додаткова вправа. Відшукати геометричний спосіб доведення формули

 

( вказівка – використати ілюстрацію для обчислення суми арифметичної прогресії із першим членом  1 та різницею арифметичної прогресії 1 або відомий факт із біографії К. Гаусса).

 

Урок №2

Тема уроку. Метод математичної індукції та його застосування

Мета уроку. Формувати в учнів навики застосування методу математичної індукції для доведення нерівностей. Розвивати логічне мислення, культуру математичного мовлення , письма, креативність. Виховувати наполегливість, свідоме ставлення до навчання, пізнавальні інтереси учнів.

Обладнання :  дидактичний матеріал , портрет Я.Бернуллі, опорна схема

Тип уроку : комбінований.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

На дошці  2 учні виконують вправу 1, додаткову вправу, на місці – 2 учні-індивідуальне завдання.

Клас. Повторюють схему розв’язування вправ з використанням методу математичної індукції та виконують вправу.

Вправа. Вивести та довести формулу для обчислення суми

Розв’язання. Помічаємо, що

Можливо формула матиме вигляд

Доведемо її методом математичної індукції.

1) База індукції .Істинність рівності , коли , вже встановлено.

2) Індуктивний перехід. Припустимо, що коли  ,

 сума

Доведемо її істинність , якщо . Справді,

За принципом математичної індукції , припущення істинне при всіх натуральних .

ІІ спосіб виконання вправи. Дану формулу можна було довести іншим способом , помітивши закономірність та розклавши кожен доданок у різницю двох простих дробів таким чином:

Тоді матимемо:

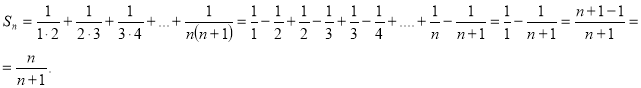ІІІ. Повідомлення теми та мети  уроку. Мотивація пізнавальної діяльності учнів

IV.Формування нових знань

Учитель .

Узагальнення методу математичної індукції.

 Часто трапляється , що твердження , яке треба довести має місце не для всіх натуральних , а лише для значень , починаючи з певного натурального . У таких випадках користуються узагальненим принципом математичної індукції. Сформулюємо цей принцип.

 Нехай твердження , що залежить від натурального , задовольняє такі умови : 1) це твердження істинне при ;2)з правильності даного твердження при (для ) випливає його правильність при . Тоді дане твердження справджується при всіх натуральних .

За допомогою методу математичної індукції можна довести важливу нерівність – нерівність Бернуллі, названу так на честь швейцарського математика Якоба Бернуллі.

Довести, що для всіх і всіх натуральних виконується нерівність        .

Доведення. 1) База індукції. Якщо , то маємо правильну нерівність

2) Індуктивний перехід. Нехай нерівність істинна  при . Тоді доведемо, що нерівність також істинна.

Оскільки , то і тому маємо :

.

Отже, за принципом математичної індукції , істинність нерівності Бернуллі доведена для всіх натуральних значень .

V. Застосування знань. Формування вмінь

Вправа.(Колективне розв’язання) Довести нерівність

 

Доведення. Вираз, що стоїть у лівій частині нерівності є сумою дробів, знаменники яких послідовно зростають від 1 до .

1) База індукції. Якщо , то дана нерівність матиме вигляд і є правильною.

2) Індуктивний перехід. Припустимо, що , і доведемо тоді , що правильною є і така нерівність

 

Розглянемо суму

, де вираз позначений А є сумою дробів , кожен з яких більший від . Отже, і тоді

Отже, за принципом математичної індукції , істинність нерівності  доведена для всіх натуральних значень .

Вправа.(метод «Коло ідей») Розв’язати нерівність .

Розв’язання. Безпосередня перевірка показує, що числа та не є розв’язками нерівності , а значення , , є її розв’язками. Природно виникає припущення, що розв’язками даної нерівності є натуральні  числа . Доведемо це твердження методом математичної індукції.

1) База індукції. Якщо , то нерівність правильна

2) Індуктивний перехід. Припустимо, що коли , нерівність правильна, тобто , і доведемо, що тоді

Справді , оскільки для будь – яких натуральних .

 Тобто , якщо , . Тому розв’язками даної нерівності є всі натуральні числа .

Вправа. Довести нерівність .

Доведення. 1) База індукції. Якщо , то очевидна нерівність

2) Індукційний перехід .Якщо , то істинна нерівність і доведемо нерівність при , тобто

.

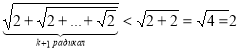Отже ,нерівність істинна при будь – якому натуральному

Хвилинка-цікавинка. Чи знаєте ви що?..

Бернуллі – сім’я швейцарських математиків. Родоначальником сімейства є Якоб Бернуллі( помер у 1583 році). Народився в Голландії. Його внук Якоб Бернуллі (1598-1634 рр.) мешкав у Базелі. Багато членів сімейства були відомими діячами, займали високі державні посади. Історії математики відомо імена принаймні 10 відомих математиків та фізиків із сімейства Бернуллі.

Вправа. Довести нерівність

Доведення. 1) База індукції. Якщо , то очевидна нерівність

2) Індукційний перехід. Якщо , то істинна нерівність

Доведемо істинність при , тобто

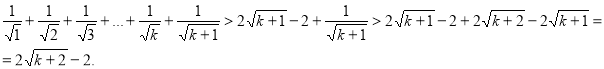
Нерівність можна довести методом від супротивного.

Отже, вихідна нерівність справедлива при будь –якому натуральному VI. Підсумок уроку. Цінування та оцінювання

Рефлексія. Яке завдання уроку було найскладнішим  і найпростішим?

Яких додаткових знань потребує розв’язування таких вправ?

VIІ . Домашнє завдання

Вправа .Довести нерівність: .

Повторити:  ознаки подільності натуральних чисел та розкладання на множники , якщо число - непарне.

 

Урок №3

Тема уроку. Метод математичної індукції та його застосування

Мета уроку. Формувати в учнів навики застосування методу математичної індукції для доведення подільності виразів. Розвивати логічне мислення, культуру математичного мовлення , письма, креативність. Виховувати наполегливість, свідоме ставлення до навчання, пізнавальні інтереси учнів, вміння працювати в парах.

Обладнання :  дидактичний матеріал , опорна схема.

Тип уроку : формування вмінь та навиків.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

 Учні виконують перевірку домашнього завдання по готових записах на дошці.

ІІІ. Актуалізація опорних знань учнів

 Сформулювати ознаки подільності чисел на 2,5,,3,9,10.

 Записати формули розкладу виразів , якщо число - непарне та формули , якщо - довільне число.

IV.Мотивація пізнавальної діяльності учнів

 Але ознаки подільності не завжди дозволяють довести подільність виразів на те чи інше число, на той чи інший вираз. І тут на допомогу  може прийти метод математичної індукції.

V. Повідомлення теми та мети уроку

 На сьогоднішньому уроці ми розглянемо, ще одну сферу застосування методу математичної індукції – доведення подільності виразів. Крім цього ми пригадаємо , як деякі з них можна розв’язати іншим способом , показавши цим самим варіативність розв’язання однієї і тієї ж задачі,

VІ. Первинне засвоєння матеріалу

Пояснення вчителя.

Вправа. Довести, що кратне 7,

Доведення. 1)База індукції. Якщо , то маємо:

2) Індукційний перехід. Припустимо, що коли вираз і доведемо , що вираз кратний 7 при .

Отже, Твердження доведено для всіх

ІІ спосіб.. Дане твердження можна було довести , використавши відому формулу для розкладу , якщо число - непарне.

.

VІІ. Вироблення вмінь та навиків

Робота організовується в групах. Клас поділено на три групи. Захищати розв’язання вправи буде один із представників групи.(застосувати метод «навчаючи – вчуся»).

Завдання для першої групи

Вправа . Довести, що числа виду  кратні 9,

Доведення. 1) База індукції. Якщо , то маємо :

2) Індукційний перехід. Припустимо, що коли вираз  і доведемо, що коли вираз теж кратний 9.

Отже, Дане твердження справедливе для всіх

Завдання для другої групи

Вправа. Довести, що вираз ділиться на 133.

Доведення.1)База індукції. Якщо , то маємо    

2) Індуктивний перехід. Припустимо, що коли : ,

тобто і розглянемо вираз , коли .

Отримаємо :

 Виконаємо перетворення :

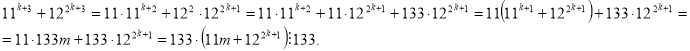 За принципом математичної індукції , істинність твердження доведена для всіх натуральних .

Завдання для третьої групи

Вправа. Довести, що кратне 27,

Доведення. 1)База індукції. Якщо , то маємо

2) Індуктивний перехід. Припустимо, що коли вираз і доведемо, що вираз кратний 27, якщо

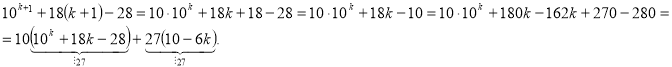 Отже, .

Дане твердження істинне для всіх

VІІІ. Підсумок уроку. Цінування та оцінювання відповідей учнів

ІХ. Домашнє завдання.

Повторити формули  для знаходження кількості діагоналей довільного многокутника, суми внутрішніх кутів довільного многокутника.

Вправа. Довеcти , що 4.

Додатково.(Завдання олімпіадного характеру) Довести, що число 11….1 ( одиниць) ділиться на .

Доведення. 1)База індукції. Якщо , то число 111 ділиться на 3 (за ознакою подільності на 3). 

Якщо , то число 111 111 111 ділиться на 9 (за ознакою подільності на 9).

Або 111 111 111 = 111*1001001. Кожен з множників ділиться на 3, а тому добуток ділиться на 9.

Якщо , то число 111…1 (27 одиниць) ділиться на 27, бо його можна представити . Перший множник ділиться на 9, а другий - на 3, тому число ділиться на 27.

2) Індуктивний перехід.  Припустимо, що коли , то число ділиться на і доведемо , що число ділиться на .

 Виконаємо перетворення :  . Перший множник ділиться на за індуктивним припущенням, а другий – на 3(за ознакою подільності), тому добуток ділиться на .

 За принципом математичної індукції , істинність твердження доведена для всіх натуральних .

 

Урок №4

Тема уроку. Метод математичної індукції та його застосування

  (Метод математичної індукції в геометрії)

Мета уроку. Формувати в учнів навики застосування методу математичної індукції для розв’язування геометричних вправ. Розвивати логічне мислення, культуру математичного мовлення , письма, креслярські навики, креативність. Виховувати наполегливість, свідоме ставлення до навчання, пізнавальні інтереси учнів.

Обладнання :  опорна схема» метод математичної індукції», креслярські прилади, портрет Софі Жермен.

Девіз уроку : Алгебра і геометрія – єдині країни , де панують мир та злагода (Софі Жермен).

Тип уроку : формування вмінь та навиків.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання

На дошці розглядається розв’язування завдання олімпіадного характеру, в кількох учнів перевіряється виконання домашнього завдання та виставляється оцінка до класного журналу.

ІІІ. Актуалізація опорних знань учнів

 Повторити :

- формули для знаходження кількості діагоналей довільного многокутника, суми внутрішніх кутів довільного многокутника,

- схему розв’язування вправ методом математичної індукції

IV.Повідомлення теми , мети , девізу уроку. Мотивація пізнавальної діяльності учнів

V. Формування вмінь

Вправа . Довести, що загальна кількість діагоналей опуклого многокутника обчислюється за формулою , де - кількість сторін .

Доведення. 1) База індукції. Очевидно , що  при ( для трикутника) формула справедлива, бо .

2) Індуктивний перехід. Припустимо , що дана формула справедлива для , тобто загальна кількість діагоналей опуклого - кутника буде визначатись формулою  Добудуємо до даного - кутника одну вершину і утворимо ()- кутник. Нову вершину можна з’єднати з вершинами вихідного многокутника, перебудованого нами в - кутник. Крім того одна з сторін многокутника перетворилась на діагональ. Тому загальна кількість діагоналей утвореного многокутника обчислюється за формулою .

Отже, загальна кількість діагоналей довільного опуклого многокутника обчислюється за формулою

Вправа. Довести, що сума внутрішніх кутів опуклого многокутника обчислюється за формулою , де - кількість кутів многокутника.

Доведення. 1) База індукції . При утвориться трикутник , а така теорема про суму кутів трикутника відома. .

2) Індуктивний перехід. Припустимо, що сума кутів - кутника  обчислюється за формулою . Добавимо ще одну вершину , утвориться - кутник. Тоді сума його внутрішніх кутів дорівнює сумі кутів - кутника   та кутів трикутника, тобто

 За принципом математичної індукції дане твердження справедливе для будь – якого - кутника.

Інформативна хвилина. Софі Жермен (01.04.1770- 27.06.1831) - французький математик і філософ. Народилася в Парижі. З дитинства захоплювалась математичними працями, особливо історії математики .Оскільки в той час жінок не приймали до Політехнічної школи, вона користувалась конспектами лекцій, приймала участь в обговоренні під псевдонімом Леблан. Вела переписку з Д’Аламбером, Фур’є, Гауссом, Лежандром. Займалась теорією чисел, довела велику теорему Ферма для . Жермен є одним із засновників математичної фізики. За дослідження в теорії пружності ( теорії згину пластинок) отримала премію Паризької АН (1811) – це була перша премія , видана  Паризькою академією наук жінці. Задачу «Довести , що будь – яке число виду є складене (a>1) « називається задачею Жермен.

Вправа. Площину поділено на області кількома прямими . Дві області називаються сусідніми , якщо їх межею є або відрізок, або промінь, або пряма. Довести, що ці області можна пофарбувати в два кольори так, щоб сусідні області мали різний колір.

Розв’язання. Нехай на площині проведено прямих. Індуктивні міркування проводитимуться по кількості прямих.

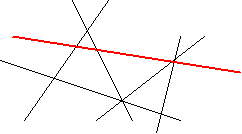
1) База індукції. Очевидно, що при твердження задачі є правильним ( рис.1)

 

 Рис.2

 

                Рис.1                                                               Рис.2

2) Індуктивний перехід. Припустимо, що дане твердження є правильним при , тобто області, утворені прямими, можна розфарбувати належним чином. Нехай на площині проведено пряму . Подумки вилучимо одну з цих прямих ( на рис. 2 це червона пряма) , тоді на площині залишиться прямих, і за припущенням вони задають області, які можна пофарбувати потрібним чином (рис.3).

 Кольори всіх областей, що лежать у нижній півплощині відносно червоної прямої , поміняємо на протилежні , а кольори областей, які лежать у верхній півплощині , залишимо без змін. Утворений малюнок задовольняє умову задачі (рис.4).

                                                                                            

 

               Рис.3                                                            Рис.4

VІ. Підсумок уроку

 Що нового дізнались на сьогоднішньому уроці?

 Чи переконались в істинності слів Софі Жермен : «Алгебра і геометрія – єдині країни , де панують мир та злагода»?

VІІ. Цінування та оцінювання учнів

VІІІ. Домашнє завдання

Вправа. Довести, що для будь – якого натурального , існує опуклий многокутник , який має рівно три гострих кути.(Вказівка. «Відрізати» тупий кут в  будь – якому - кутнику )

 

 

 

 

 

РОЗДІЛ 2

ЗАСТОСУВАННЯ МЕТОДУ МАТЕМАТИЧНОЇ ІНДУКЦІЇ ДО РОЗВ’ЯЗУВАННЯ ВПРАВ

 

 В даному розділі вміщений практичний матеріал, який можна використати додатково при проведенні уроків , при підготовці учнів до олімпіад з математики, контрольних робіт при захисті науково - дослідницьких робіт МАН України, при проведенні занять математичних гуртків та факультативів.

2.1. Метод математичної індукції в розв’язуванні задач на підсумовування та доведення тотожностей

Приклад 1. Довести, що  .

Доведення. 1) База індукції .Якщо , то .

2)Індукційний перехід .Припустимо істинність твердження при , тобто та доведемо істинність при , тобто .

 Отже, рівність справедлива для будь - якого

ІІ спосіб доведення. Очевидно, що .Тепер можна записати

                              

Приклад 2  .Вивести і довести формулу для обчислення суми

Розв’язання. Оскільки

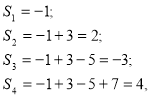
то виникає гіпотеза , що

Доведемо це методом математичної індукції.

1)База індукції. Істинність рівності , коли , вже встановлено.

2) Індуктивний перехід. Припустимо, що коли  , сума обчислюється за формулою

Доведемо, що сума можна обчислити за формулою

Справді

Отже , твердження істинне при , а з його істинності при , випливає його істинність при . За принципом математичної індукції , припущення істинне при всіх натуральних .

Приклад 3. Вивести та довести формулу для обчислення суми , де .

Розв’язання.

Для :

для

для

для

Тепер можна зробити таке припущення :.

Враховуючи, що відома формула для знаходження суми перших натуральних чисел, дану формулу можна записати таким чином :

Справедливість формули для було встановлено вище. Нехай дана формула справедлива для , тобто

Маємо:

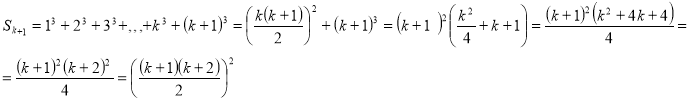 Отже , твердження істинне при , а з його істинності при , випливає його істинність при . За принципом математичної індукції , припущення істинне при всіх натуральних .0

Приклад 4. Довести, що для .

Доведення. 1) База індукції. Якщо , ліва частина даної тотожності набуває вигляду , а права - . Отже, якщо , то дана рівність правильна.

2). Індуктивний перехід. Припустимо, що рівність виконується , якщо , тобто . Доведемо, що вона істинна , коли , тобто 

.

Розглянемо ліву частину рівності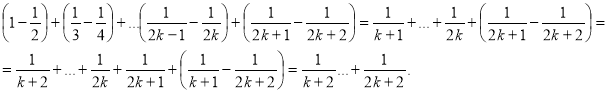

Отже, з істинності твердження при випливає її істинність при . Тому за принципом математичної індукції, тотожність доведена для всіх натуральних .

Приклад 5. Довести, що

Доведення . 1) База індукції. Якщо , то

2) Індуктивний перехід . Якщо , то істинне твердження 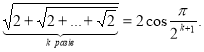та доведемо істинність твердження при , тобто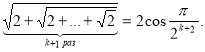

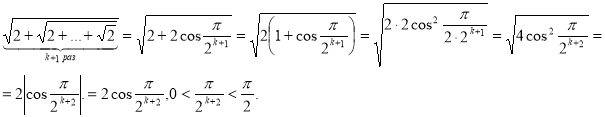
Отже, дане твердження істинне для всіх

Приклад 6. Довести тотожність .

Доведення . 1) База індукції. Якщо , то тотожність справедлива оскільки

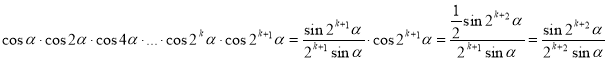2) Індуктивний перехід . Якщо , то істинне твердження, тобто . Доведемо, що вона справедлива при . Дійсно .               Отже, з істинності твердження при випливає її істинність при . Тому за принципом математичної індукції, тотожність доведена для всіх натуральних .

Приклад 7. Довести, що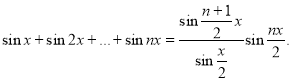

Доведення . 1) База індукції. Якщо , то тотожність справедлива.

2) Індуктивний перехід . Якщо , то істинне твердження, тобто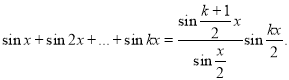

 Тоді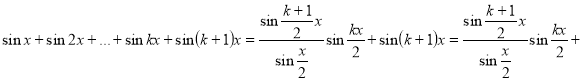

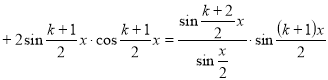,оскільки

 

Отже, з істинності твердження при випливає її істинність при . Тому за принципом математичної індукції, тотожність доведена для всіх натуральних .

Приклад 8. Довести, що .

Доведення . 1) База індукції. Якщо , то істинне твердження.

2) Індуктивний перехід . Якщо , то істинне твердження, тобто і доведемо , що дана формула істинна при .

Дійсно

Отже, з істинності твердження при випливає її істинність при . Тому за принципом математичної індукції, тотожність доведена для всіх натуральних .

 

2.2.  Доведення нерівностей за допомогою методу математичної індукції

Приклад 9. Довести, що для всіх натуральних , виконується нерівність

Розв’язання. Піднесемо обидві частини нерівності , що треба довести , до степеня . Отримаємо нерівність або тобто  .

Останню нерівність доводимо методом  математичної індукції.

1)База індукції. Якщо , то ліва частина матиме вигляд:

а нерівність набуває вигляду і є правильною .

2) Індуктивний перехід. Нехай, коли , нерівність правильна: .

Доведемо, що істинною  буде нерівність і тоді , коли : .

Розглянемо ліву частину :

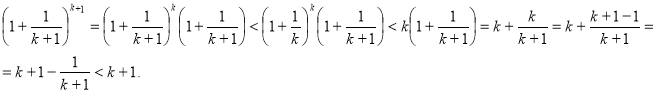 За принципом математичної індукції нерівність істинна , а отже , істинна і нерівність для всіх натуральних .

Приклад 32. Довести, що для всіх виконується нерівність.

Доведення.  1)База індукції. Якщо , то .

2)Індукційний перехід. Припустимо, що твердження істинне при , тобто і доведемо істинність при .

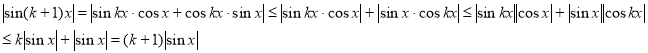 Тут використано припущення та нерівність ( область значень тригонометричної функції).

2.3. Задачі на подільність

Приклад 35. Довести, що числа виду кратні 6.

Доведення. 1) База індукції.

2) Індукційний перехід. Нехай . Доведемо, що коли ,

 .

.

Отже,

Зауваження . Дане твердження можна було довести іншим способом, використовуючи відому формулу 

Приклад 36. Довести, що кратне 6,

Доведення. 1) База індукції. Якщо , то маємо .

2) Індукційний перехід. Припустимо, що коли вираз і доведемо , що вираз кратний 6 при .

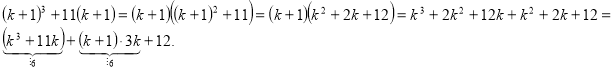
Оскільки , то .

Отже, . Дане твердження істинне для всіх

Приклад 37. Довести, що ділиться на 6 для всіх натуральних .

Доведення.  Доведемо, що вираз ділиться на 6 для всіх натуральних .

1)База індукції. Якщо , то маємо , тобто вираз , даний в умові , є числом цілим.

2)Індуктивний перехід. Припустимо, що коли , вираз ділиться на 6, тобто   і доведемо, що також ділиться на 6. Перетворимо цей вираз:

 Отриманий добуток обов’язково кратний 6, оскільки є добутком трьох послідовних натуральних чисел.

 Отже, за принципом математичної індукції, вираз є цілим числом для всіх натуральних .

Приклад 38. Довести, що значення виразу кратне 7.

Доведення. 1)База індукції. Якщо , то маємо

2)Індуктивний перехід. Припустимо, що коли вираз і доведемо , що вираз кратний 7 при Для доведення достатньо показати, що різниця кратна 7, тобто

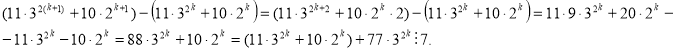 Оскільки за припущенням і

Отже, твердження, що доводиться ,є правильним.

Дане твердження можна було довести іншим способом.

Оскільки вираз кратний 7 для будь – якого натурального і вираз , то і весь вираз кратний 7.

Приклад 39. Послідовність задається  такими умовами:

    Знайти формулу - го члена послідовності.

Розв’язання. Скористаємось рекурентним співвідношенням , матимемо:

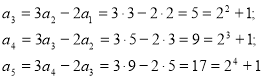      і т.д.

Виникає гіпотеза , що .

Доведемо це твердження методом математичної індукції.

1) База індукції. Якщо , то твердження правильне.

2) Індуктивний перехід. Припустимо, що твердження правильне для всіх натуральних , , і доведемо, що воно істинне і коли :

     

 Отже, за узагальненим принципом математичної індукції , твердження правильне для всіх натуральних .

Приклад 40. Довести , що сума кубів трьох послідовних натуральних чисел кратна 9.

Доведення. 1)База індукції. Сума ділиться на 9. Отже, твердження істинне, якщо першим із трьох послідовних чисел буде 1.

2) Індуктивний перехід.  Припустимо, що коли вираз, де - натуральне число ділиться на 9.  Покажемо істинність твердження , коли , тобто

Даний вираз кратний 9, оскільки перший вираз в дужках ділиться на 9 за припущенням, а другий – ділиться на 9 , бо це – добуток двох множників , один , з яких дорівнює 9.

За принципом математичної індукції , істинність твердження доведена для всіх натуральних .

Приклад 41 .Довести, що при будь якому натуральному ділиться на 11.

Доведення. 1)База індукції. Якщо , то число ділиться на 11.

2) Індуктивний перехід.  Припустимо, що коли вираз ділиться на 11 без остачі і доведемо, що твердження істинне при .

.

 Перший доданок ділиться на 11 без остачі згідно припущення, другий доданок ділиться на 11 без остачі, тому що один з його множників є число 11.Отже, сума ділиться на 11 без остачі.

За принципом математичної індукції , істинність твердження доведена для всіх натуральних .

Приклад 42. Довести, що при будь – якому натуральному ділиться на 6 без остачі.

Доведення. 1)База індукції. Якщо , то число ділиться на 6.

2) Індуктивний перехід. Припустимо, що коли вираз ділиться на 6 та доведемо , то даний вираз ділиться на 6, якщо .

.

Обидва доданки діляться на 6 без остачі : перший містить число 120, яке кратне 6, а другий ділиться на 6 без остачі згідно припущення.

 За принципом математичної індукції , істинність твердження доведена для всіх натуральних .

Зауваження .Дане твердження можна було довести без використання методу математичної індукції.

       

 Даний добуток ділиться на 6, оскільки один з множниківділиться на 6 без остачі.

 

2.4 Вивчення властивостей числових послідовностей

Арифметична та геометрична послідовності визначаються рекурентними співвідношеннями та  відповідно. За допомогою методу математичної індукції можна довести ці формули, а також формули для знаходження суми перших членів цих відомих послідовностей.

Приклад 12. Довести формулу -го члена арифметичної прогресії

Доведення. 1). База індукції. Якщо ,то формула набуває вигляду :

2). Індуктивний перехід. Припустимо, що коли , правильною є формула , і доведемо істинність  при , тобто .

За принципом математичної індукції  формула для  -го члена арифметичної прогресії є правильною для будь – яких натуральних значень .

Приклад 13. Довести , що суму перших членів геометричної прогресії можна обчислити за формулою

де - перший член послідовності, - знаменник геометричної прогресії

Розв’язання. Розглянемо два випадки.

1. Якщо , то , тобто формула є правильною.

2. Якщо , то скористаємось методом математичної індукції.

1) База індукції. Якщо , то формула набуває вигляду і є істинною.

2) Індуктивний перехід. Припустимо, що коли , правильною є формула і доведемо, що коли , має місце співвідношення

Враховуючи, що та припущення індукції матимемо :

 

 За принципом математичної індукції  формула для знаходження суми перших членів геометричної прогресії є правильною для будь – яких натуральних значень .

Приклад 14. Послідовність задана рекурентно : .Довести, що цю послідовність можна задати формулою го члена

Доведення. Доведення проведемо методом математичної індукції.

Якщо , то твердження правильне, бо .

Якщо , то твердження правильне, бо

Нехай і Маємо:

 Тим самим формула істинна для будь - якого натурального .

2.5 Вивчення властивостей скінчених множин

Розглянемо питання про кількість підмножини скінченої множини .

 Якщо Х=Ø, то вона має лише одну підмножину : Ø.

 Якщо Х- одноелементна множина, то її підмножинами будуть множини Ø та Х.

 Якщо , то її підмножинами будуть множини: Ø, .

 Якщо , то підмножинами будуть : ,Ø.

Позначимо кількість підмножин - елементної множини через . Тоді з розглянутих прикладів випливає, що :

Виникає припущення , що кількість підмножин  - елементної множини дорівнює . Доведемо цю гіпотезу методом математичної індукції.

1) База індукції. Гіпотезу перевірено , коли .

2) Індуктивний перехід .Припустимо, що твердження правильне, коли , тобто , будь – яка - елементна множина має підмножин. Доведемо правильність твердження при , тобто довільна - елементна множина має підмножин.

 Нехай множину отримали з множини включенням до неї одного елемента . Будь – яка з підмножин множини Х або не містить його, тоді вона є множиною , або містить , тоді відкинувши ,отримаємо знову деяку підмножину множини . У першому випадку маємо підмножин, у другому випадку - теж підмножин.

 Але тоді загальна кількість підмножин множини Х дорівнюватиме

.

 Отже, доведено, що рівність істинна , коли , і   з її істинності при , випливає істинність при . За принципом математичної індукції  робимо висновок, що твердження справедливе для довільних натуральних .

2.6. Математична індукція в геометрії

Приклад 15. Довести, що різних точок , що належать одній прямій, розбивають її на інтервал ( з яких два є нескінченними)

Доведення. 1) База індукції. Якщо , то дане твердження є істинним , оскільки одна точка поділяє пряму на 1+1=2 інтервали.

2) Індуктивний перехід .Припустимо, що дане твердження істинне , коли ( тобто різних точок розбивають пряму на () інтервал).

 Далі довільно виберемо на прямій точку: . Якщо відкинути одну точку , то залишиться точок, що поділяють пряму на () інтервал. Точка належить одному з цих інтервалів і поділяє його на два інтервали. Тому загальна кількість інтервалів, на які поділяють пряму () точка дорівнює .

 Отже, твердження істинне , коли , а з його істинності , коли , випливає його істинність і коли  . За принципом математичної індукції, воно істинне для всіх натуральних  .

Приклад 16. На площині проведено різних кіл так, що кожні два з них перетинаються в двох точках і ніякі три з них не мають спільної точки. На скільки частин поділяють площину ці кола?

Розв’язання. Дослідимо питання про кількість частин. Одне коло поділяє площину на 2 частини; два кола – на 2+2=4 частини , три кола – на частин; чотири кола – на частин і т.д.

 Виникає гіпотеза, що різних кіл поділяють площину на частин. Доведемо її, використовуючи метод математичної індукції.

1) База індукції .Якщо , то дане твердження є істинним .

2) Індуктивний перехід .Припустимо, що дане твердження істинне , коли . Тобто кіл поділяють площину на частин. Врахуємо, що кожне - ше коло додасть стільки само частин до поділу , скільки утвориться точок перетину кіл. Тобто попередня кількість частин площини збільшиться на . Отже, () -  коло поділяє площину на частини.

 За принципом математичної індукції , гіпотеза є правильною: різних кіл , що задовольняють умову задачі, поділяють площину на частини.

Приклад 17. Довести, що сторона правильного ,вписаного в коло , - кутника , виражається формулою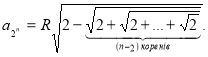

Доведення. 1) База індукції. За змістом . Коли , отримаємо правильний чотирикутник – квадрат. Справді , сторона квадрата .

2) Індуктивний перехід . Припустимо, що дане твердження істинне , коли , тобто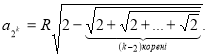

Доведемо дану формулу , якщо .

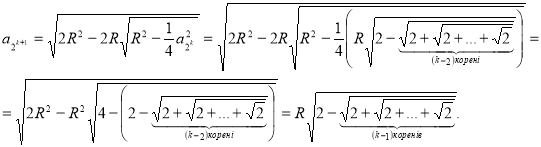
Дане твердження доведено для всіх ,

Приклад 18. Дано прямих на площині, причому ніякі дві з них не паралельні і ніякі три не проходять через одну точку. На скільки частин поділяють площину ці прямі?

Розв’язання. Якщо , то таких частин .

Якщо , то таких частин

Якщо , то таких частин

Якщо , то таких частин

Виникає гіпотеза, що при перетині прямих площина поділиться на кількість частин, що обчислюється за формулою:

.

Якщо ця формула вірна, то при перетині ще однієї прямої для всіх прямих з’явиться нова частина, так що .

Приклад 19. На скільки частин розбиває простір площин, із яких кожні три перетинаються і ніякі чотири не мають спільної точки?

Розв’язання. Зрозуміло, що , де - кількість частин, на які розбивають простір  площин. Проведемо четверту площину і припустимо, що вона розбила простір на частин. Три перші площини, які розбили простір на частини, перетнуть четверту по трьох напрямках, із яких кожні дві перетинаються , але всі три не мають спільної точки. Таким чином , четверта площина розіб’ється першими трьома на частин .Це означає, що чотири площини розіб’ють простір на () частин. Можна припустити, що

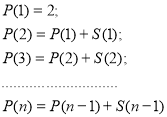
Складемо ці рівності. Одержимо:

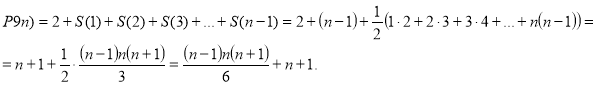
Для доведення формул, що в дужках, скористаємось методом математичної індукції.

Таким чином , .

Проведемо -шу  площину  так, щоб вона перетинала всі площин і щоб ніякі чотири не мали спільної точки. Тоді площин перетнуть -шу площину по прямих, із яких кожні дві перетинаються, але всі три не мають спільної точки.

 Ці прямих розбивають -шу площину на частин. Це означає , що всі площини розбивають весь простір на частин.

Таким чином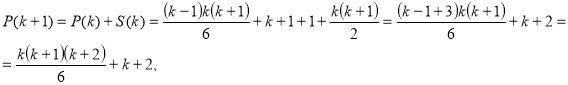

 Що й треба було довести.

2.7. Застосування методу математичної індукції до доведення деяких  теорем

Теорема 1. Квадрат многочленна рівний сумі квадратів всіх його членів , доданих до все можливих подвоєних попарних добутків, тобто

           .

Доведення. 1)База індукції. Якщо ,то формула очевидна.

Якщо , то формулу можна довести безпосередньо перемноживши .

2) Індуктивний перехід. Припустимо, що коли має місце формула :

.

Доведемо, що де - сума всіх можливих попарних добутків , складених із , тобто .

Дійсно ,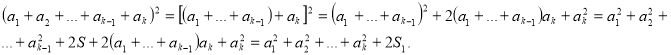

За принципом математичної індукції , істинність формули  доведена для всіх натуральних .

Теорема 2. Число перестановок з елементів обчислюється за формулою

Доведення. 1)База індукції. Якщо ,то формула очевидна.

2) Індуктивний перехід. Припустимо, що коли має місце формула

Покажемо, що . Із даних   елементів візьмемо лише перші і складемо із них всі можливі перестановки, їх буде .

 В кожній з цих перестановок поставимо елемент послідовно перед 1-м елементом, 2- елементом, …, - елементом, після -го елемента. Цим шляхом ми із однієї перестановки з елементів отримали перестановку із елемента. Всього отримаємо перестановок із елемента.

 Отже, .

За принципом математичної індукції , істинність формули  доведена для всіх натуральних .

Теорема 3. Число розміщень із по може бути обчислена за формулою

.

Доведення. 1)База індукції. Якщо , то слід відмітити, що , тому формула справедлива.

2) Індуктивний перехід. Припустимо, що коли має місце формула

. Доведемо, що

Для отримання всіх розміщень із елементів по елемент достатньо взяти всі розміщення з елементів по і до кожного з них приписати в кінці кожен із залишених   елементів. Неважко переконатися, щ складені таким чином розміщення із елементів по елемент всі різні і крім того , всяке розміщення з елементів по елемент міститься  серед отриманих.

 Таким чином

 За принципом математичної індукції , істинність формули  доведена для всіх натуральних .

Теорема 4. Число комбінацій з по обчислюється за формулою

                                                     .

Доведення. 1)База індукції. Якщо , то слід відмітити, що і тому формула справедлива.

2) Індуктивний перехід. Припустимо, що коли має місце формула

.

Доведемо, що .

Для отримання всіх комбінацій з по випишемо всі комбінації з по і до кожного з них в якості - го елемента приєднаємо кожен із елементів, що залишились.

 Таким чином будуть отримані всі комбінації із елементів по , але кожна із них отримаються раз.

 Дійсно , комбінації отримуються, коли до комбінації приєднати елемент , коли до комбінації  приєднати елемент і т.д., коли, нарешті, до комбінації приєднати елемент . Таким чином,

.

 За принципом математичної індукції , істинність формули  доведена для всіх натуральних .

Теорема 5. (Біном Ньютона) Які б не були числа та і яке б не було натуральне число має місце формула :

                                    

Доведення. 1)База індукції. Якщо , то

2) Індуктивний перехід. Припустимо, що коли має місце формула:

                                

 Доведемо , що формула справедлива і при .

 Справді

Приймаючи до уваги , що , отримаємо :

Отже, за принципом математичної індукції, дана формула справедлива для будь – якого натурального .

Теорема 6. Якщо в результаті скінченого числа раціональних дій (тобто додавання, віднімання, множення, ділення)над комплексними числами отримали число , то  в результаті таких же дій над спряженими числами отримаємо число , спряжене з числом .

Доведення. 1)База індукції. Покажемо істинність теореми для двох комплексних чисел. Нехай , .

Тоді ,

 .

Аналогічно це твердження перевіряється для інших арифметичних дій.

2) Нехай тепер дано деякий раціональний вираз від комплексних чисел .Обчислення такого виразу зводиться , як відомо, до послідовного виконання однієї з чотирьох арифметичних дій над двома комплексними числами, причому дії можуть бути занумерованими.

Наприклад, нехай . Для обчислення достатньо  виконати дії :

 Припустимо, що твердження вірне для всіх виразів, які обчислюються не більше діями. Термін «дія» тут означає або дію додавання, або віднімання, або множення , або ділення двох комплексних чисел. Покажемо , що твердження справедливе і тоді , коли над виразами необхідно виконати дію.

 Дійсно, останню () дію ми виконуємо над числами та , які самі обчислюються через виконання не більше ніж дій. В результаті заміни спряженими, числа і також замінюються спряженими та , а тоді і результат  () -  дії над ними , тобто числа ,заміниться на спряжене число .

 За принципом математичної індукції , твердження істинне для будь – якого натурального .

2.8.  Різні схеми застосування методу математичної індукції

Розглянемо одну з форм доведення методом математичної індукції, що відрізняється від попередньої.

Нехай і - числові послідовності. Якщо для деякого натурального числа справедлива нерівність і для всіх справедлива нерівність , то для всіх справедлива нерівність .

Дещо видозміненою формою доведення методом математичної індукції є наступна. Якщо для деякого натурального числа справедлива нерівність і для всіх справедлива нерівність , то для всіх справедлива нерівність .

Приклад 43. Довести нерівність , де

Доведення

Розглянемо дві послідовності  і , де , .

1) База індукції .Якщо  , то і, очевидно,  .

2) Індуктивний перехід. Нехай , тоді

Доведемо, що , тобто таку нерівність:

Замінимо цю нерівність рівносильною, виконавши тотожні перетворення

.

Остання нерівність очевидна, тому й вихідна нерівність правильна.

Приклад 44.Знайти усі натуральні значення , при яких .

Розв’язання.

Введемо позначення . У пошуках гіпотези природно знайти значення для декількох значень .

Маємо:

при ;

при

при ;

при

при ;

при

Тепер можна зробити таке припущення :

при

не кратне 7  при

Методом математичної індукції нескладно довести такі три твердження:

 

.

Проте даний приклад можна було розв’язати , використовуючи метод математичної індукції з кроком 3.

База індукції: не кратне 7.

Для доведення достатньо показати, що .

Приклад 45. Число     таке, що       - ціле. Довести, що  для будь- якого натурального число     є також  ціле.                                                                                                                                                        
Розв’язання.

При твердження є правильним. Припустимо, що при число є цілим.

Справедливою є така рівність

З неї випливає, що число є цілим, якщо цілим є не тільки число , але й число . Але в індуктивному переході такої умови немає.

Бачимо, що для розв’язання цієї задачі схему доведення методом математичної індукції слід відкоригувати таким чином : в « індуктивному переході» зробити припущення , що твердження , яке доводиться , справедливе при і , а далі довести , що воно справедливе при .

 Ця зміна , в свою чергу потребує перевірки в базі індукції  не тільки для , але й для .

Маємо : . Отже, число   є цілим, оскільки цілим є число .

Для розв’язання цієї задачі довелося посилити умову індуктивного переходу , при цьому крок індукції залишився рівним 1.

Тому схему методу математичної індукції можна описати так:

1) Установити справедливість твердження при ;

2) З припущення , що гіпотеза є правильною для всіх , довести її справедливість для .

Приклад 46. Довести, що будь – яке натуральне число можна подати у вигляді суми кількох різних степенів числа 2 (включаючи нульовий).

Розв’язання.

При маємо .

Нехай твердження є справедливим для всіх натуральних таких, що , . Розглянемо натуральне число .

 Якщо це число є степенем числа 2, то теорему «індуктивний перехід» доведено. Якщо, число не є степенем числа 2, то існує натуральне число таке, що . Звідси .

 Якщо припустити, що , то , що суперечить нерівності  . Отже, . Але , отже, .

 Маємо: .Тоді за індуктивним припущенням число можна подати у вигляді суми різних степенів числа 2, при чому серед цих доданків немає числа . Додавши до цієї суми число , отримаємо шукане подання числа .

Приклад 47. Для невід’ємних , де довести нерівність .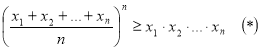

Як правило цю нерівність записують у вигляді і називають нерівністю Коші.

Розв’язання.

  Якщо , то нерівність (*)є правильною. Подальші міркування проводитимуться для випадку , коли .

 При маємо : Справедливість цієї нерівності випливає з нерівності Коші для двох чисел.

 Нехай нерівність (*) є правильною для , тобто

.

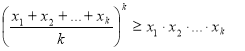Доведемо, що вона є правильною для .

Маємо:

Ми показали, що нерівність (*) є правильною для . Отже, вона є правильною для , а тоді вона є правильною при , при

, при і взагалі , при всіх натуральних значеннях таких, що

 Таким чином хвиля доведеним тверджень розповсюджується за схемою:

Залишилося показати що ця «хвиля» може розповсюджуватись у зворотному порядку  з кроком 1:

Для цього слід припустити, що нерівність (*) є правильною для , і довести, що вона є правильною для .

 Коли нерівність є правильною для будь – яких невід’ємних , то вона є справедливою і для випадку , коли . Запишемо цей випадок:

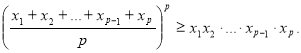
Маємо: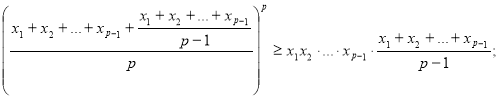

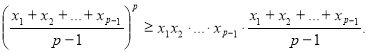
Поділивши обидві частини цієї нерівності на додатне число , отримаємо .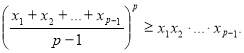

 Цим завершимо доведення нерівності (*).

Приклад 48. Довести, що довільну суму , більшу 7 копійок , можна сплатити монетами вартістю в 3 коп. та 5 коп.

Доведення. 1)База індукції. Суму в 8 копійок , очевидно можна сплатити.

2) Індуктивний перехід. Припустимо, що нам вдалося сплатити суму в копійок вказаними монетами. Якщо серед них є монета в 5 коп., то замінимо її на дві монети по 3 коп. і одержимо суму в   копійку. Якщо ж всі монети суми по 3 коп., то їх не менше трьох, і замінивши три монети по 3 коп. на дві монети по 5 коп., ми також збільшимо суму на 1 копійку.

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Математика. Посібник для факультативних занять / [ Вивальнюк Л.М., Соколенко О.І., Боровик В.Н.] . –К.: Освіта ,1993.- 176 с.

2. Мерзляк А.Г. Алгебра . Підручник для 9 класу з поглибленим вивченням математики / Мерзляк А.Г.,Полонський В.Б. ,Якір М.С. –Харків: Гімназія, 2009. -378 с.

3. Методика факультативних занятий в 9-10 классах. Избранные вопросы математики / [Антипов И.Н, Березин В.Н., Егоров А.А.] –Москва : Просвещение, 1983 .- 176 с.

4. Науково - дослідницька робота учнів  з математики в Малій академії наук /  [Лагно В.І., Мельниченко О.С., Карапузова Н. Д., Ільченко О .О ., Ворона Л.І.] . – Полтава: ПДПУ, 2009. – 256 с.

5. Нелін Є. П. Алгебра і початки аналізу , 10 клас / Нелін Є.П.- Харків: Світ дитинства, 2008. – 448 с.

6. Приймаков О.Г. Вибрані розділи математики / Приймаков О.Г., Молявко О.І. - Харків : Скорпіон, 2004. – 236 с.

7. Семенов В.О. Доведення нерівностей . Числові послідовності: скінчені суми і добутки / Семенов В.О.   – Харків : Основа , 2009. -128 с.

8. Яремчук Ф.П. Алгебра и элементарные функции / Яремчук Ф.П., Рудченко П.А. –Киев: Наукова  думка, 1997.- 686 с.

9. Ясінський В. А. Задачі математичних олімпіад та методи їх розв’язування / Ясінський В. А. – Тернопіль: Навчальна книга , 2006. – 208 с.