"Нестандартные способы решения уравнений, систем уравнений. Уравнения с двумя переменными и системы двух уравнений с тремя переменными"
Урок
Тема. Нестандартные способы решения уравнений, систем уравнений. Уравнения с двумя переменными и системы двух уравнений с тремя переменными
( бинарный урок алгебры в 11 классе).
Цели:
- образовательная: обеспечить овладение основными алгоритмическими приемами в решении уравнений;
- воспитательная: сформировать умение наблюдать закономерности, обобщать, проводить рассуждения.
Ход работы.
l. Вступление. Организационный момент.
Учащиеся к гостям поворачиваются лицом. Учитель произносит слова:
« Приветствуем гостей, пришедших к нам сегодня.
Улыбки старшеклассников желают счастья Вам, здоровья
Мы постараемся на славу потрудиться
Чтоб, милые учителя вам было чем гордиться».
Эпиграф нашего сегодняшнего урока мне хотелось бы сформулировать словами М.В.Ломоносова: «И мыслям надобно учиться, но более
В сто крат важнее – учиться мыслить».
( Эти слова эпиграфом записаны на ватмане и прикреплены возле доски (слева)).
Это значит, что сегодня мы будем учиться применять теоретические и практические знания при решении уравнений, систем. Будем учиться быть внимательными и наблюдательными.
ll. Основная часть урока.
Домашнее задание я проверю, собрав сегодня ваши тетради, а сейчас мы сразу включаемся в работу.
У доски два человека решают самостоятельно уравнения, с последующим комментированием контрольных моментов (способа решения)
-
х2+2х+
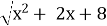 - 12=0;
- 12=0;
Метод уединения радикала приводит к уравнению четвертой степени, поэтому положим
![]() = y, y≥0, х2+2х+8=y;
= y, y≥0, х2+2х+8=y;
х2-8+y-12=0;
![]()
![]() y2+y-20=0; у1+у2=-1; у1=-5.
y2+y-20=0; у1+у2=-1; у1=-5.
у1·у2=-20; у2=4.
![]() Отсюда
Отсюда ![]() =4
=4
х1+х2=-1; х1=-4. х2+2х-8=0.
х1·х2=-20; х2=2.
ОДЗ: х2+2х-8≥0
Ответ:-4;2.
-
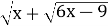 +
+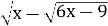 =
=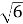 ;
;
ОДЗ: 6х-9≥0;
х+![]() ≥0;
≥0;
х-![]() ≥0.
≥0.
Возводим в квадрат обе части уравнения, получим:
2х+2·lх-3l=6
![]()
![]() х+lх-3l=3
х+lх-3l=3
х![]() (-
(-![]() ) х
) х![]() -
-![]() )
)
х-(х-3)=3 2х=6
3=3 х=3![]() -
-![]() )
)
х![]() -
-![]() )
)
Тождество значит ![]() -
-![]() ; 3)
; 3)
Общий ответ для этих уравнений х![]() (-
(-![]() ), а учитывая ОДЗ, ответом данного уравнения будет х
), а учитывая ОДЗ, ответом данного уравнения будет х![]() .
.
Ответ: ![]()
( 1 ряд делится пополам, и решают вместе с доской). В это время на проекторе класс рассматривает задание № 1 «Найти ОДЗ уравнений» (в конце прилагается). Послушать вопросы и задания к двум номерам, рассмотренных у доски.
Затем 3 и 2 ряды списывают с проектора задание №2 «Определить с помощью графика число корней уравнения».
3 ряд – расм. № 1,2; 2 ряд - № 3,4 (выполняют самостоятельно в тетрадях), а 1 ряд рассматривает со мной на проекторе задание № 3 «Приключения с уравнениями».
Во время этого разбора у доски трое учащихся решают уравнения. (Пока они еще решают, я с места (уже после задания № 3)проверяю количество корней уравнения и могу пригласить к переносной доске изобразить рисунки).
2 и 3 ряды после выполнения задания 2 думают над различными способами решения уравнения х(х+1)(х+2)(х+3)=120.
Решить уравнения:
-
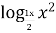 - 14
- 14 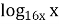 3 + 40
3 + 40 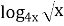 =0
=0
Формула перехода к новому основанию не может применяться, если основания логарифмов равны 1. Поэтому сначала надо проверить х=1- корень уравнения? Только когда утверждаемся, что х=1 – корень, и для х![]() 1, применяем указанную формулу
1, применяем указанную формулу
![]() -
- ![]() +
+ ![]() =0
=0
Пусть ![]() =y, имеем
=y, имеем ![]()
То 2y2-3y-2=0; y'•+y•”=-3 у•'=-4. Тогда у1=-2.
y2+3y•- 4=0; y’•*y•”=-4 у•"=1. у2=-![]() .
.
![]() = -2
= -2 ![]() =
=![]()
![]() = -
= -![]()
![]() = 2
= 2
Отсюда x=![]() =
=![]() и х=4
и х=4
Ответ: 1; 4; ![]() .
.
-
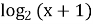 +0,5
+0,5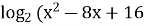 )=1
)=1
Здесь нельзя поверхностно применять свойства логарифма
![]() =2
=2![]() имеет место лишь для х>4, (т.е. сужается ОДЗ и происходит потеря корней).
имеет место лишь для х>4, (т.е. сужается ОДЗ и происходит потеря корней).
Правильной будет следующая запись ![]() =2
=2![]() .
.
Итак, ![]() +
+![]() . (х+1)|х-4|=6.
. (х+1)|х-4|=6.
Решать его надо для двух случаев ОДЗ: -1<х<4 и х>4.
-(х+1)(х-4)=6 -(х+1)(х-4)=6
-(х2-3х-4)-6=0 х2-3х-10=0
-х2+3х-2=0 х3=-2 не является корнем; х4=5;
х1=1; х2=2.
Проверяем принадлежность корней к рассматриваемым промежуткам.
Ответ: 1;2;5.
Если пойти первым путем, то теряются корни 1 и 2.
Решить уравнение ![]() =
=![]() .
.
![]() ·
·![]() =
=![]() ;|·3х, так как х=0-не корень уравнения.
;|·3х, так как х=0-не корень уравнения.
![]() ·
·![]() +3·
+3·![]() =3·х
=3·х![]() -3·х
-3·х![]() ;
;
![]() ·
·![]() +2·х
+2·х![]() -3·х
-3·х![]() +3·х
+3·х![]() +3·
+3·![]() =0;
=0;
![]() ·
·![]() +
+![]() ·
·![]() -3·х
-3·х![]() -3·
-3·![]() =0;
=0;
![]()
![]()
![]()
![]() ·
·![]() +х·(
+х·(![]() -3·
-3·![]() )- 3·
)- 3·![]() =0;
=0;
а в с
D=(![]() )2-4·
)2-4·![]() ·
·![]() =
=![]() 6·
6·![]() +9·
+9·![]() =(
=(![]() )2>0.
)2>0.
х1,2=![]()
х1=-1; х2=3·![]() /
/![]() .
.
Ответ: х1=-1; х2=3·![]() /
/![]() .
.
1 ряд, после выполнения задания № 3 из проектора записывает любое из трех уравнений себе в тетрадь. В то время 2 и 3 ряды слушают объяснения контрольных моментов в этих уравнениях и записывают не достающие у них способы решения х(х+1)(х+2)(х+3)=120(всего 4 способа).
На этом этапе все группы завершают свою работу и со всем классом провожу программированный опрос(карточки для ответа у каждого лежат на парте , а задание отображено на проекторе: задание № 4 «Программированный опрос»).
Через несколько минут ребята сдают свои карточки на первую парту , и я по коду проверяю количество «5», «4», «3».
Правильный код: 4343.
lll. А сейчас переходим ко второй половине нашего урока.
Высвечиваю на проекторе «Нестандартные способы решения уравнений и их систем»(прилагается в конце плана). Обговариваем эти способы с классом. Дальше выписываю на доске 18 уравнений и фронтально (с места) работаем с учащимися по определению способа решения того или иного уравнения и, если удается, то сразу называем его корни.
|
Условия |
Примечания |
|
Графический х1=0 , х2=-2 |
|
ограниченность и монотонность. А как еще можно решить
|
|
монотонность, х=1
|
|
|
если есть решение, то оно единственное 2 - const |
|
|
Х=2 подбором и делаем проверку, корень единственный |
|
7)
|
Использование ограниченности |х+у| здесь идет выход на нахождение общих корней (диофрантово уравнение) |
|
8) |
1) ОДЗ: -1 2) f(-х)=f(х) – четная
f(0)=2; f(1)= f(-1)=
f(х)=
но |
|
9) 3х+4х=5х
(
|
Х=2, Пифагоровы числа Делим на наибольшее число 5х, убывающая функция может принимать свое значение только один раз, 1 - const |
|
3х=2
х= |
Пифагоровы числа |
|
11) 2|х|+ |
Ограниченность 2|х|+
Отсюда 2|х|=1; х=0; 2· |
|
12) 2|х|+ |
Нет решений. Почему? |
|
13) tgх+ сtgх= |
Взаимообратные а+1/а |
|
14) |
Ограниченность обозначений [0;1] Умин=1
Единственный корень х=1 |
|
15) 1+
|
(Из сборника Сканави) ограниченность
1+
Х=
|
|
16) (ДГМА)
|
Неравенство Коши(решим у доски) |
|
17) |
Пойдет как д/з неравенство Коши |
|
18) |
Рейтинговое задание ДонГУ
тригонометрическая подстановка х=
х= |
№ 16
![]() +
+![]() =30-
=30-![]() -4
-4![]()
![]() -
-![]() +(
+(![]() )=30
)=30
Для каждой скобки применим неравенство Коши: а+в/2![]()
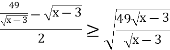 ;
; ![]() +
+![]() 14, аналогично
14, аналогично ![]()
и тогда равенство достигается, когда оба равны по 14 и 16 и решаем отдельно два уравнения
![]() +
+![]() 14 и
14 и ![]() .
.
пусть ![]() =t, t>0 пусть
=t, t>0 пусть ![]() =m, m>0
=m, m>0
![]() + t=14
+ t=14 ![]() +4m=16
+4m=16
![]() =0
=0 ![]() =0
=0
(t-7)2=0 (2m-4)2=0
t=7 m=2
Отсюда ![]() =7 Отсюда
=7 Отсюда ![]() =2
=2
х-3=49 у-4=4
х=52 у=0
Ответ: (52;8).
№ 18
![]() +2х2=1
+2х2=1
Пусть х=![]() , t
, t![]() [
[![]() ] (или х=
] (или х=![]() , t
, t![]() [0;
[0; ![]() ])
])
|
2sin2t+ sin2t-1=0
sin2t=у; |у| 2у2+у-1=0 у1=-1; у2=1/2 |
Отсюда sin2t=-1 и sin2t=
2t=-
t=-
т.к. t
t1=- к=1, то
t2= к=2 |
х1=![]() =-
=-![]()
Имеем тогда: х2=![]()
х3=![]()
Ответ: ![]() ;
; ![]() ;
; ![]() =
=![]()
Эти задания записывают все учащиеся класса и слушают ответы одноклассников. К доске приглашают еще два человека для решения следующих уравнений, а класс работает вместе с отвечающими, но дается параллельно задание(сильным учащимся): Изобразить ОДЗ функции (ДГМА).
№ 1251(экз.сб.школьный)
х2+4х![]() +4=0
+4=0
Решаем как квадратное уравнение
D1=4cos2(ху)-4![]() 0
0
cos2(ху)![]() 0 учитывая ограниченность функции у=cosх [-1;1]
0 учитывая ограниченность функции у=cosх [-1;1]
cos2(ху)=1 Отсюда cos(ху)=1 или cos(ху)=-1
С этими условиями из первоначального уравнения получаем два:
х2+4х+4=0 х2-4х-4=0
х=-2 х=2
Тогда cos(-2у)=1 Тогда cos(2у)=-1
-2у=3![]() к 2у=
к 2у=![]() +2
+2![]() к
к
у=-![]() к, к
к, к![]() Z у=
Z у=![]() , к
, к![]() Z
Z
Ответ: (-2; -![]() к, к
к, к![]() Z), (2;
Z), (2; ![]() +
+![]() к, к
к, к![]() Z).
Z).
№ ДГМА Решить систему
![]()
![]()
![]() х2+1=2
х2+1=2![]() х2=2
х2=2![]() х2
х2![]() ,
,
у2-1=2хz![]() у2-1=2хz
у2-1=2хz![]()
![]() значит, 2
значит, 2![]() -1
-1![]() 4уz
4уz![]()
![]()
![]() 4уz
4уz![]()
Отсюда 4уz![]()
Подставим эту замену в первоначальную систему:
![]()
![]() х2=0 х=0 Тогда z=
х2=0 х=0 Тогда z=![]()
у2-1=0 у=![]()
Ответ: (0;1;1/4) (0;-1;-1/4).
Затем всем учащимся класса предлагается самостоятельно найти целочисленные решения системы №4263 (ДГМА)
![]() х+10=у+z
х+10=у+z
уz=10х+1
А в это время эту же систему один ученик решает на «крыле» доски, чтобы никто не видел решения. Затем класс проверяет свое решение по образцу:
![]() х+10=у+z
х+10=у+z
уz=10х+1
Отсюда можно составить квадратное уравнение (по т. Виета)
к2-(10+х)к+10х+1=0
D=(10+х)2-4(10х+1)=х2-20х+96=(х-10)2-4=0
(х-10)2=4
Отсюда х-10=2 х-10=-2
х1=12 х2=8.
![]() Тогда
Тогда
![]()
![]()
![]() х+10=у+z у=11
х+10=у+z у=11
![]() уz=10х+1 z=11
уz=10х+1 z=11
![]()
![]() х+10=у+z у=9
х+10=у+z у=9
уz=10х+1 z=9
Ответ: (12; 11; 11); (8;9;9).
после проверки этой самостоятельной работы, учащиеся показывают, как они справились с дополнительным заданием.
В системе координат х,у изобразить множество точек, для которых формула имеет смысл z=![]()
![]()
![]()
![]() ОДЗ:
ОДЗ: ![]()

![]()
![]()
![]()
![]()
![]()
![]() y=2-х/2
y=2-х/2 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Формула имеет смысл для
Формула имеет смысл для
![]()
![]()

![]() всех точек, расположенных
всех точек, расположенных
![]()
![]()
![]()
![]()
![]() внутри ромба со стороной
внутри ромба со стороной
у=2-х/2 (в 1 чет), исключая точки, имеющие целочисленные координаты.
IV. Учащимся предлагается записать домашнее задание.
Решить следующие уравнения(взяты со сборника ДГМА)
-
х2+
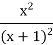 =
=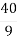
- (2х2-3х+1)( 2х2+5х+1)=9х2
-
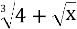 +
+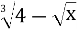 =
=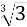
-
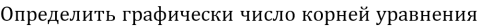
х2-2х-![]() =3
=3
(х-1)![]() -х=1
-х=1
V. Итог урока подводит учитель.
Идея поведения такого урока не была неожиданной. У ребят старших
классов часто наблюдается прагматическое отношение к математике – выучить, чтобы сдать экзамен; сдать экзамен, чтобы поступить в вуз. Думается, что одним из объяснений подобного потребительского отношения является претупление познавательного интереса, прекрасного качества, подаренного человеку природой. Ученики перестали ощущать и ценить (а может быть, никогда и не чувствовали) внутри предметную красоту математики, силу ее эмоционального воздействия. Мне кажется, что действенным средством эстетического воздействия математики на учеников являются задачи, и именно те задачи, которые мы называем красивыми. А что же такое красивая задача? И уместно ли задачи наградить эпитетом «красивая»?
Я предлагаю учащимся посмотреть на плакат, на котором написана формула математической красоты, предложенная В.Г.Болтянским (ж. МШ № 2 , 1982 г.).
Красивая задача = непредсказуемость + неожиданность + удивительная простота + фантазия + удивление+ оптимизм+ труд+…
И предложила учащимся продолжить этот перечень, как итог нашего урока. звучали разные дополнения, а один учащийся предложил на 1-е место поставить «вдохновение».
Дополнить эту формулу можно стихотворением учащегося этого класса Голубенка Александра, которое он написал еще вначале 9-го класса.
Когда говоришь: «Математика»,
То вспоминаешь слова:
«Четкость», «ясность», «порядок»,
Силу людского ума.
Так же как ветер могучий
Силу движенье дает,
Древняя цифр наука
Технику движет вперед.
Вера и труд – вот слагаемые
Нашего счастья, а мы
Следствие лишь теоремы
К жизни стремленья, любви.
Есть красота в математике!
Она, словно чудный алмаз:
Законы тверды, нерушимы,
Свет ее радует глаз.
Но, это ясно конечно,
Не будет жизнь никогда
Четкой последовательностью событий,
Ровной гладью стекла.
Ее предсказать невозможно!
И формул таких не ищи.
Вечно в расчеты врывается
Корень из минус один.
А это стихотворение написано Сашей две недели назад и посвящается своим одноклассникам и математике, которая их объединяла эти три года. Читает стихотворение участница областного конкурса чтецов Скряга Ирина.
Мы можем думать, нам дано мыслить
Проще простого нырнуть
В пресные волны знаков и чисел –
Только бы не утонуть
Мы можем думать, нам дано мыслить
В крепкие клетки страниц
Почерком синим ясность и четкость
Будет легко заманить.
Мы можем думать, нам дано мыслить
Жаль, что не всем дано
Терпкий вкус формул знать, и решений
Пить молодое вино.
Спасибо вам большое ребята. Урок окончен.
Приложения
Задания для проектора
Задание №1 (первый кадр)
Найти ОДЗ уравнений
-
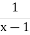 =
=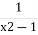
-
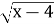 +
+ =3
=3
-
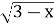 =x
=x
-
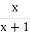 =lg (4-x2)
=lg (4-x2)
-
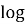 2(x2-x-6)=
2(x2-x-6)=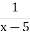
-
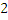 x=-
x=-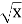
Ответы: (общая часть)
1) x![]() (-
(-![]() ;-1)U (-1;1)U (1;+
;-1)U (-1;1)U (1;+![]()
2) 0
3) x![]() [0;3]
[0;3]
4) x ![]() (-2;-1)U [0;2)
(-2;-1)U [0;2)
5) x ![]() (-
(-![]() ;-2) U (3;5)U (5; +
;-2) U (3;5)U (5; +![]()
6) x ![]() [0;+
[0;+![]()
Добавьте дополнительные условия так, чтобы были равносильны уравнения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание № 2 (второй кадр)
Определите с помощью графика число корней уравнения:
- 2х=3-2х-х2
-
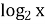 =х2+х-2
=х2+х-2
-
 =1/2х-1/2
=1/2х-1/2
- х5=10х-1
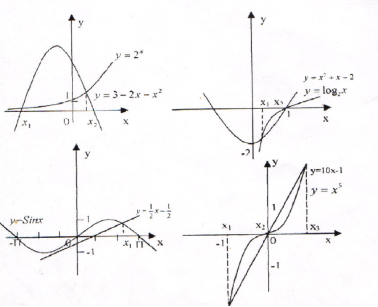
Задание № 3
Приключения с уравнениями (найти ошибку в решении и объяснить ее)
№1: 5x-25+20=4x; 5x-25=4x-20; 5(x-5)=4x(x-5); 5=4 ?
№2: ![]() +
+![]() +
+![]() =1;
=1; ![]() =1;
=1; ![]() =1; 2=0 ?
=1; 2=0 ?
№ 3: ![]() -5=
-5=![]() ;
; ![]() ;
; ![]() ;
;
![]() ; 13-х=7-х; 13=7 ?
; 13-х=7-х; 13=7 ?
Нет корней?
№ 4
![]() х4-1321х-23=0; (1)
х4-1321х-23=0; (1)
х4-1310х-144=0; (2)
![]() (1)- (2) -11х+121=0; х=11.
(1)- (2) -11х+121=0; х=11.
Не является корнем каждого уравнения. Почему?
Задание № 4.
Программированный опрос
№ 1 Какое уравнение имеет по крайней мере один корень на множестве целых чисел?
- 9х2-9х+2=0 3) х6+х3-6=0
- х4-2х2-3=0 4) х4+х2+х=0
№ 2 Какое уравнение имеет корень?
-
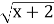 +2=0 3) 10х=
+2=0 3) 10х=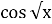
-
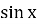 +
+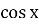 =2 4)
=2 4) 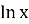 =lх
=lх
№ 3 Дана система уравнений:
![]() у=х2+а
у=х2+а
х2=у2
Какое утверждение ложное?
- не может иметь единственное решение;
- может иметь три решения;
- может иметь четыре решения;
- может иметь более четырех.
№ 4 Какие два уравнения равносильны?
-
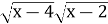 =
=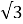 и
и 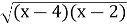 =
=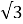
-
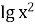 =2 и
=2 и 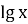 =1
=1
-
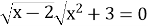 и
и 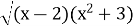 =
=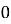
-
х3=1 и
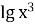 =
=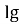 1
1
Правильный код: 4343
lV способ: Он основан на тождестве
х(х+1)(х+2)(х+3)+1=(х2+3х+1)2 и тогда
![]()
![]()
![]() (х2+3х+1)2=121 х2+3х+1=11 есть действительные корни х=2; х=-5
(х2+3х+1)2=121 х2+3х+1=11 есть действительные корни х=2; х=-5
х2+3х+1=-1 нет действит. корней
Ответ: 2;-5.
Таблица
«Нестандартные способы решений уравнений и их систем»
- Использование ОДЗ;
- Использование монотонности;
- Использование ограниченности(оценка областей значения функции);
- Использование классических неравенств:
а) ![]() , где а
, где а![]() (неравенство Коши)
(неравенство Коши)
б) а+![]() , при а
, при а![]()
в) (1+х)к![]() 1+кх, где х
1+кх, где х![]() (неравенство Бернулли)
(неравенство Бернулли)
5. Тригонометрическая подстановка
х=![]() , х=
, х=![]()
Способы решения уравнения
х(х+1)(х+2)(х+3)=120
1 способ: Воспользуемся симметрией левой части, перемножим 1) и 4) множители, а 2) и 3) между собой (х2+3х)(х2+3х+2)=120.
Пусть х2+3х=у у(у+2)=120
Отсюда у1=-12, у2=10, тогда
х2+3х=-12 и х2+3х=10
D=-39-нет дейст. корней х2+3х-10=0
х1=-5; х2=2.
Ответ:-5;2.
ll способ: Симметрией можно воспользоваться иначе. Заметим, что числа х, х+1, х+2, х+3 расположены на числовой оси симметрично относительно числа х+3/2. замена х+3/2=у, тогда уравнение примет вид (у-3/2)(у-1/2)(у+1/2)(у+3/2)=120;
(у2-9/4)(у2-1/4)=120. Пусть у2=z, z![]() 0 и дальше идет обычное решение квадратного уравнения.
0 и дальше идет обычное решение квадратного уравнения.
lll способ: Перемножим все скобки, получим уравнение :
х4+6х3+11х2+6х-120=0.
Применим теорему Безу: найдем делители свободного члена: х=2 и проверим их как корни уравнения. Делим многочлен на (х-2), второе деление на многочлен (х+5).



про публікацію авторської розробки
Додати розробку
