Міні-довідник "Многогранники, тіла обертання"

Про матеріал

В міні-довіднику подані основні формули з тем «Многогранники» та «Тіла обертання». Довідник допоможе повторити та систематизувати відповідний матеріал під час підготовки до уроку, контрольної роботи, ДПА чи ЗНО. Для учнів шкіл, абітурієнтів, студентів, вчителів.

Перегляд файлу

Многогранники (площі поверхні та об’єми)

Многогранники

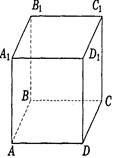
Паралелепіпед

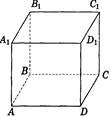
Куб

Призма

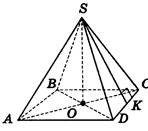
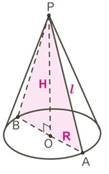
Піраміда

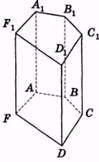
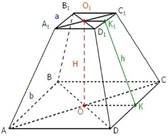
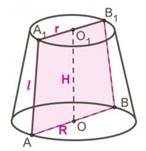
Зрізана піраміда

SK – апофема

КK₁ – апофема

S_пп (площа повної поверхні)

Sпп = Sбіч + 2Sо

S_пп = 6а²

S_пп = S_бп + 2S_о

Sпп = Sбп + Sоп

Sпп = Sбп + Sо + Sо1

S_бп (площа бічної поверхні)

S_бп = Р_о·Н

Sбп = 4а2

S_бп = Р_о Н

S_бп SK

Sбп ·КK1

Площа бічної поверхні довільної піраміди дорівнює сумі площ бічних граней піраміди

V (Об’єм)

V = S_о·Н

V = а³

V = S_о·Н

V = Н

V= S_o S_o₁ )·Н

S_о (площа основи)

Обчислюється за формулою многокутника, який лежить в основі

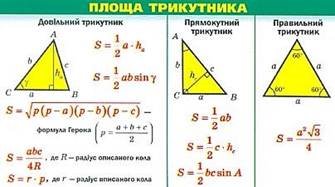
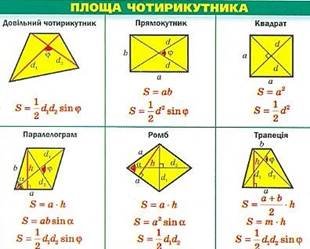
Правильні многокутники

(а – сторона, r – радіус вписаного кола, R – радіус описаного кола)

Многокутник	Співвідношення між		Площа
Многокутник	a i R	r i R	Площа
Трикутник	a = R√3	R = 2r	S = 4
Квадрат	a = R√2	R = r √2	S = a²
Шестикутник	a = R		S =
n - кутник	° a = 2Rsin	° r = Rcos	° S =

Тіла обертання (площі поверхні та об’єми)

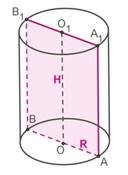
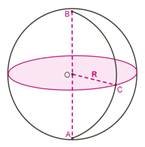
Тіла обертання	Циліндр	Конус		Зрізаний конус		Куля
S_пп (площа повної поверхні)	Sпп = Sбіч + 2Sо	Sпп = Sбіч + Sо		Sпп = Sбп + Sо + Sо1		Sсфери = 4πR2
S_бп (площа бічної поверхні)	S_бп = 2πRН	S_бп = πRl		S_бп = π(R + r) l
S_о (площа основи)	S_о = πR²	S_о = πR²		Sо = πR2, Sо1 = πr2
V (Об’єм)	V = S_оН	V = S_оН		V = )·Н		Vкулі R3
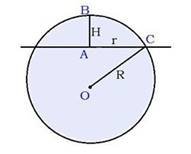
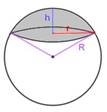
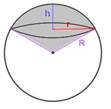
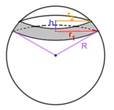
Частини кулі	Кульовий сегме S(_сегм.) = 2πRh V	нт	Кульовий сектор		Кульовий шар