Урок "Правильні многогранники"

                            Горьківська  ЗОШ І-ІІІ ст.

     Правильні многогранники 

                                                                      Урок математики у 11 класі

                                                                      підготувала і провела

                                                                      вчитель математики

                                                                      Золотар Галина Миколаївна

                                           2017/2018 н. р.

Урок по темі: «Правильні многогранники» 

Тип уроку.    Вивчення нового матеріалу.
Мета уроку.  Розглянути кожен із п’яти видів правильних многогранників. Створити умови для формування поняття правильного многогранника; навчити учнів добути  знання про властивості многогранників і познайомити їх  з історією теорії многогранників.

   Розвивати вміння спостерігати, міркувати за аналогією;просторову  уяву; практичні навички по виготовленню правильних многогранників,  інтерес до предмету через використання  інформаційних технологій та здійснення між- предметних зв'язків 

   Виховувати культуру спілкування ,  графічну культуру,  вміння працювати в групі.
Обладнання:  комп'ютери, проектор, презентація (додаток 1), картки з кросвордами, завданнями (додатоки 2,4), моделі правильних многогранників, комп'ютерний тест (додаток3).
 

 Епіграф.  Правильних многогранників надзвичайно мало,

                  але цей дуже скромний за кількістю загін зумів

              пробитись у найбільші глибини різних наук.

                                                                                                                                                                                           Л. Керролл

Хід уроку.

  1.Організаційний момент.

Повідомлення теми, мети уроку та плану роботи на урок (слайди 1,2).

Матеріал про правильні многогранники доповнює і логічно завершує розділ «Многогранники».

  2. Перевірка домашнього завдання. Усне опитування теоретичного матеріалу:

1.Який многокутник називається правильним?

( Правильні многокутники – це многокутники, у яких всі сторони і всі кути рівні.)

2.Який трикутник є правильним?

3. Як обчислити площу правильного трикутника?

4. Який чотирикутник є правильним?

5. Як обчислити площу квадрата?

6. Як обчислити площу правильного п’ятикутника?

  3. Мотивація навчання ( Слайд 3).

Вчитель. 

  Сьогодні ми вивчимо цікаву ,не тільки з точки зору математики, тему "Правильні многогранники". Тут не тільки відкривається дивовижний світ геометричних тіл, що володіють неповторними властивостями, але і цікаві наукові гіпотези.

  Ні одні геометричні тіла не володіють такою досконалістю і красою, як правильні многогранники. Зі слів Бертрана Рассела: “ Математика володіє не тільки істиною, але і вищою красою - красою відточеною й строгою, піднесено чистою і прагне до справжньої досконалості, яка властива лише найбільшим зразкам мистецтва ”.

На цьому уроці нам належить відповісти на такі питання, як, наприклад:

 Які многогранники  називаються правильними? Скільки їх існує?

Де, навіщо і для чого нам потрібні многогранники?

 Можливо, в житті можна обійтися і без них?

  4. Вивчення нового матеріалу та засвоєння нових знань і вмінь.
1)Пояснення нового матеріалу вчителем. (Слайди 4,5).

Назва “ правильні ” йде від античних часів, коли  люди прагнули знайти гармонію, правильність, досконалість в природі і людині. Правильні многогранники - це многогранники, обмежені правильними і рівними многокутниками.
ПРАВИЛЬНИЙ МНОГОГРАННИК – опуклий многогранник, грані якого є правильними многокутниками з однією і тією самою кількістю сторін і в кожній вершині якого сходиться одна і та ж кількість ребер.

2) Практичне завдання №1 (Слайд6) Робота в група.  Об’єднання в групи здійснюється заздалегідь, враховуючи рівень підготовки дітей, їх бажання

. 

3) Звіт груп про роботу - відповіді дітей (супроводжуються слайдами 7-12)

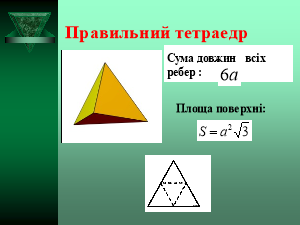
      ТЕТРАЕДР – правильний многогранник, поверхня якого складається з чотирьох правильних трикутників.
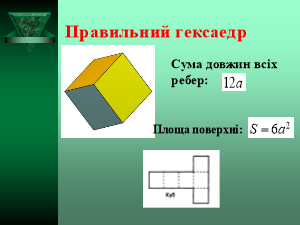
       ГЕКСАЕДР (КУБ) – правильний многогранник, поверхня якого складається з шести правильних чотирикутників (квадратів).

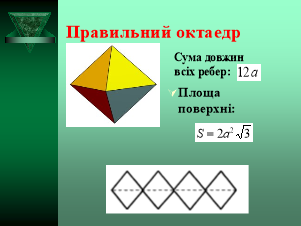
  ОКТАЕДР – правильний многогранник, поверхня якого складається з восьми правильних трикутників.

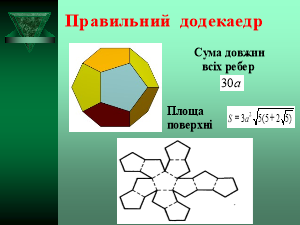
      ДОДЕКАЕДР – правильний многогранник, поверхня якого складається з дванадцяти правильних п'ятикутників.
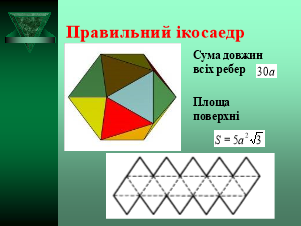
      ІКОСАЕДР – правильний многогранник, поверхня якого складається з двадцяти правильних трикутників.

4) Розповідь вчителя:(Слайд 13) Назви цих многогранників прийшли із Стародавньої Греції, і в них вказується кількість граней:

 Всі правильні многогранники були відомі ще в Стародавній Греції, і їм присвячена заключна, 13-я книга відомих “ Начал ” Евкліда. Як говорилося раніше, ці многогранники часто називають також Платоновими тілами

5)Повідомлення учня (Шульги Аліни) з комп’ютерною презентацією на  темі: «Правильні многогранники у філософській картині світу Платона» ( Слайди 14-18).

Правильні многогранники іноді називають Платоновими тілами, оскільки вони займають чільне місце у філософській картині світу, розробленій великим мислителем Стародавньої Греції Платоном ( 428 - 348 до н.е.).
Платон вважав, що світ будується з чотирьох «стихій» - вогню, землі, повітря і води, а атоми цих «стихій» мають форму чотирьох правильних многогранників. Тетраедр уособлював вогонь, оскільки  його вершина спрямована вгору, як у полум'я, що розгорілося; ікосаедр - як обтічний - воду; куб - найстійкіша з фігур - землю, а октаедр - повітря. У наш час цю систему можна порівняти з чотирма станами речовини - твердим, рідким, газоподібним і полум'яним. П'ятий многогранник – додекаедр символізував весь світ і вважався  найголовнішим.
Це була одна з перших спроб ввести в науку ідею систематизації.
Вчитель: А зараз від наукових гіпотез перейдемо до наукових фактів

 6) Практична робота№2 
Робота в групах. Завдання диференційовані. Більш підготовлені учнів входять у 1 та 3 групи, 4-5 група - учні, які добре працюють в графічному редакторі. Розгортки, які утворяться, необхідно роздрукувати учням для виконання домашнього завдання.

1 група – знайти формули довжин ребер правильних  многогранників .
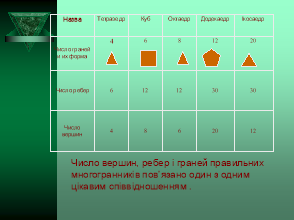
2 група – використовуючи моделі многогранників, заповнити таблицю                          «   Характеристика многогранників » і зробити висновок.

3 група – вивести формули повної поверхні правильних многогранників.
4 група - довести, що правильних многогранників 5.

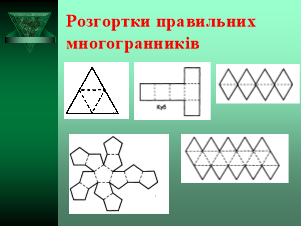
5 група – намалювати розгортки (на комп'ютері).
7). Звіт груп про роботу (10хвилин). Слайди 29,30

Один представник групи  звітує про результати біля дошки (3-4 хвилини для кожної групи).
Учні роблять відповідні записи ( формули площ; теорему Ейлера)
в зошитах.

8) Вчитель: Луї Керрол писав: " Правильних многогранників надзвичайно мало, але цей досить скромний за чисельністю загін зумів пробратися в самі глибини різних наук".
В глибини яких наук пробралися правильні многогранники? Де в житті ми можемо їх зустріти? Слайд 24.

5. Рефлексія діяльності учнів на уроці.
- Що сподобалося на уроці?
- Який матеріал був найбільш цікавий?
- Оцініть свою роботу на уроці: погано працював, добре, відмінно..
- Зв'язок геометрії, з якими науками ви побачили сьогодні на уроці?

- В яких ще сферах діяльності можна зустрітися з правильними многогранниками?    - Як ви думаєте, чи знадобляться вам знання даної теми у вашій майбутній професії?

6. Підведення підсумків. Виставлення оцінок.

 7. Домашнє  завдання:
1). (С. та д. рівні). Виготовити моделі 5 правильних многогранників.

2) (В. рівень)

Задача 1. Площа поверхні правильного ікосаедра дорівнює 360 см². Знайдіть площу однієї грані та ребро ікосаедра.

           
3) Додаткові відомості. Слайди 20-30. Деякі учні отримують завдання підготувати разом з учителями-предметниками реферати і повідомлення з конкретних тем хімії, біології,художньої культури:а) Правильні многогранники в природі.
б)Правильні многогранники в архітектурі і мистецтві.

Література:

1. Підручник: Математика, 11 клас. Рівень стандарту . За редакцією М.І. Бурди, Т.В. Колесник, Н.А. Тарасенкова , Ю.М. Мальованого, Київ: «Зодіак-ЕКО»  , 2011 .

2.  Старова  О.О. Геометрія. 11 клас. Академічний рівень. – Х. : Вид. група «Основа», 2011 . – 144 с. – (Серія «Мій конспект»).