Многогранник та його елементи. Призма,паралелепіпед, піраміда.

ЗМІСТ Многогранник та його елементи. Призма. Паралелепіпед Піраміда. Зображення піраміди Правильні многогранники ЦІКАВІ ФАКТИ ВІДЕО 1. 2.

Тема: Многогранник та його елементи. Призма. Паралелепіпед. Мета: учні повинні мати уявлення про многогранник; знати означення призми та її властивості, види призм; уміти зображати призми і застосовувати властивості призми для розв’язування задач; знати означення паралелепіпеда, його види і властивості та застосовувати їх для розв’язування задач.

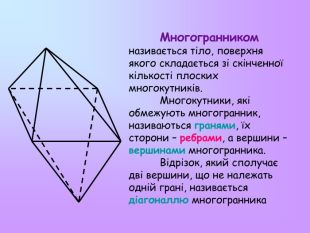
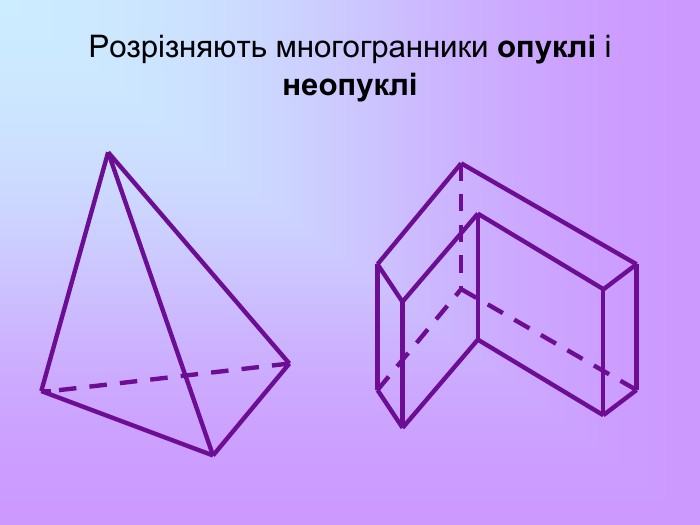
Многогранником називається тіло, поверхня якого складається зі скінченної кількості плоских многокутників. Многокутники, які обмежують многогранник, називаються гранями, їх сторони – ребрами, а вершини – вершинами многогранника. Відрізок, який сполучає дві вершини, що не належать одній грані, називається діагоналлю многогранника

Розрізняють многогранники опуклі і неопуклі

МНОГОГРАННИКИ ПРИЗМА ПАРАЛЕЛЕПІПЕД ПІРАМІДА

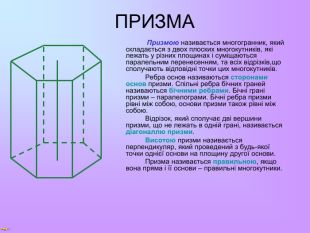
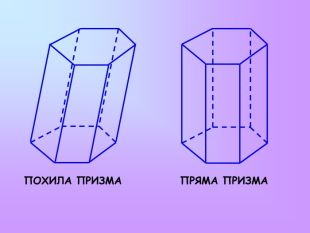
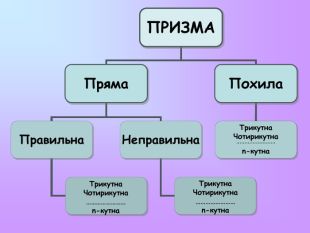
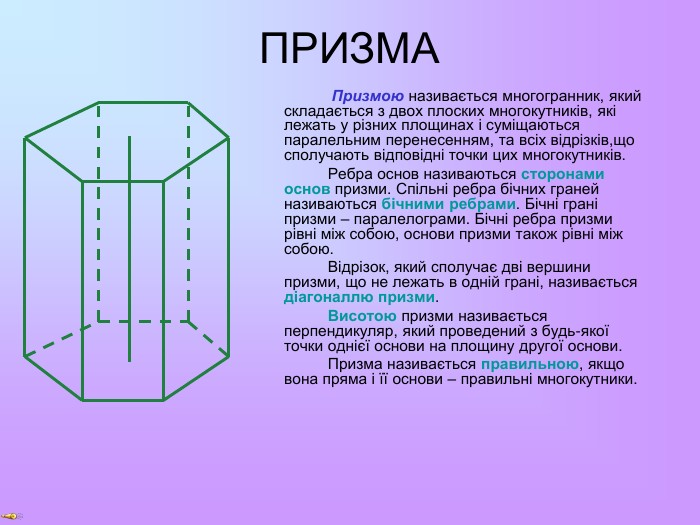
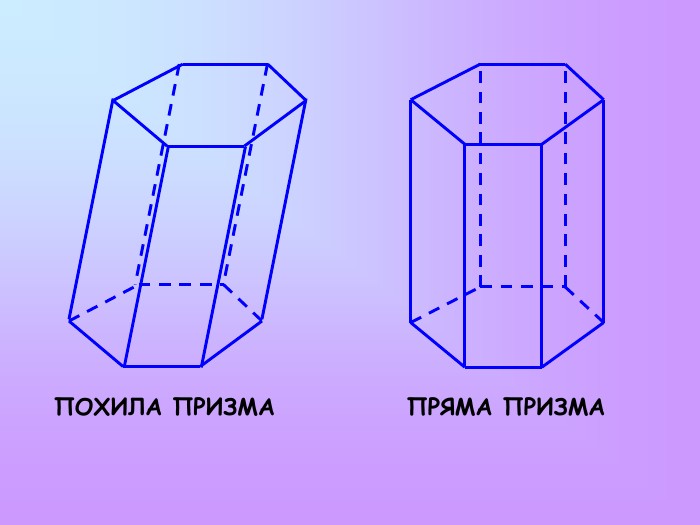
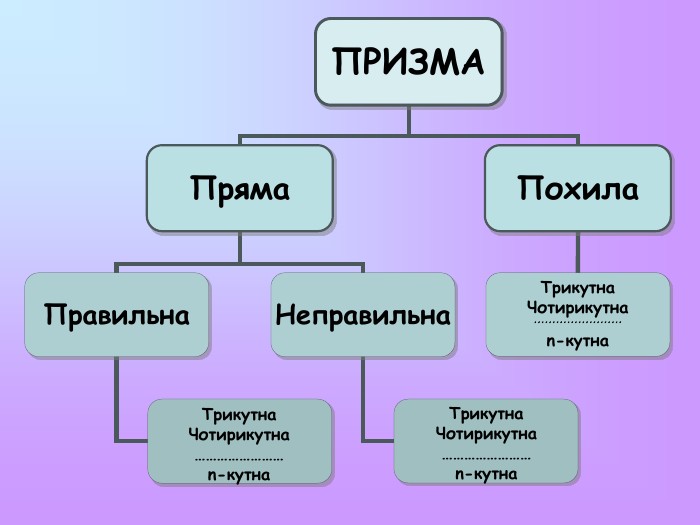
ПРИЗМА Призмою називається многогранник, який складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків,що сполучають відповідні точки цих многокутників. Ребра основ називаються сторонами основ призми. Спільні ребра бічних граней називаються бічними ребрами. Бічні грані призми – паралелограми. Бічні ребра призми рівні між собою, основи призми також рівні між собою. Відрізок, який сполучає дві вершини призми, що не лежать в одній грані, називається діагоналлю призми. Висотою призми називається перпендикуляр, який проведений з будь-якої точки однієї основи на площину другої основи. Призма називається правильною, якщо вона пряма і її основи – правильні многокутники.

ПРЯМА ПРИЗМА ПОХИЛА ПРИЗМА

ПРИЗМА Пряма Похила Правильна Неправильна Трикутна Чотирикутна …………………… n-кутна Трикутна Чотирикутна …………………… n-кутна Трикутна Чотирикутна …………………… n-кутна

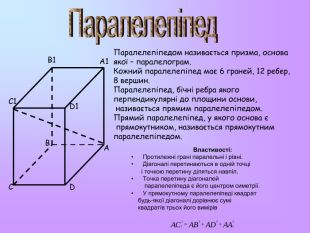
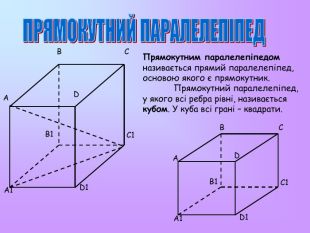
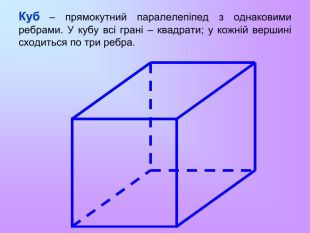
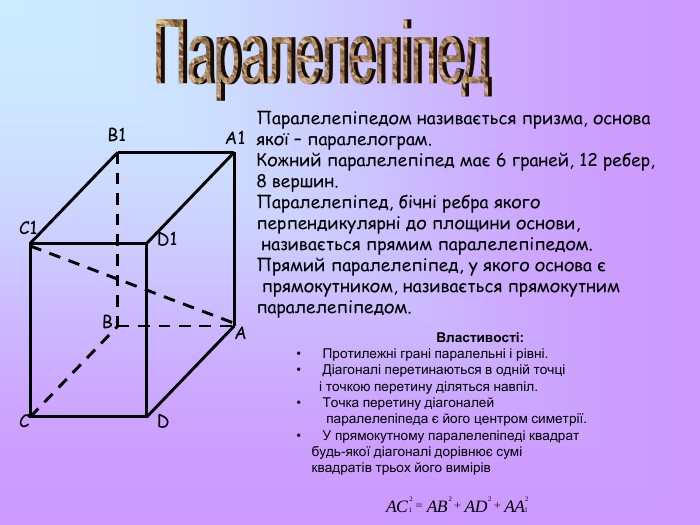
Властивості: Протилежні грані паралельні і рівні. Діагоналі перетинаються в одній точці і точкою перетину діляться навпіл. Точка перетину діагоналей паралелепіпеда є його центром симетрії. У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів Паралелепіпедом називається призма, основа якої – паралелограм. Кожний паралелепіпед має 6 граней, 12 ребер, 8 вершин. Паралелепіпед, бічні ребра якого перпендикулярні до площини основи, називається прямим паралелепіпедом. Прямий паралелепіпед, у якого основа є прямокутником, називається прямокутним паралелепіпедом. A B C D A1 B1 C1 D1

A B C D A1 B1 C1 D1 Прямокутним паралелепіпедом називається прямий паралелепіпед, основою якого є прямокутник. Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом. У куба всі грані – квадрати. A B C D A1 B1 C1 D1

Побудуйте переріз прямої трикутної призми АВСА1В1С1 площиною, що проходить через точки P і Q, які лежать відповідно на ребрах АА1 і В1С1 і точку R, яка належить грані ВВ1С1С. Побудувати переріз куба ABCDA1B1C1D1 площиною, яка проходить через три задані точки N, C, D1. ПОБУДОВА ПОБУДОВА

Мета: учні повинні знати означення піраміди і супутніх понять, означення правильної піраміди, її властивості; застосовувати властивості піраміди для розв’язування найпростіших задач; мати уявлення про перерізи піраміди площиною, вміти їх будувати; вміти розв’язувати задачі на знаходження елементів піраміди та побудову її перерізів площиною. Тема: Піраміда. Зображення піраміди

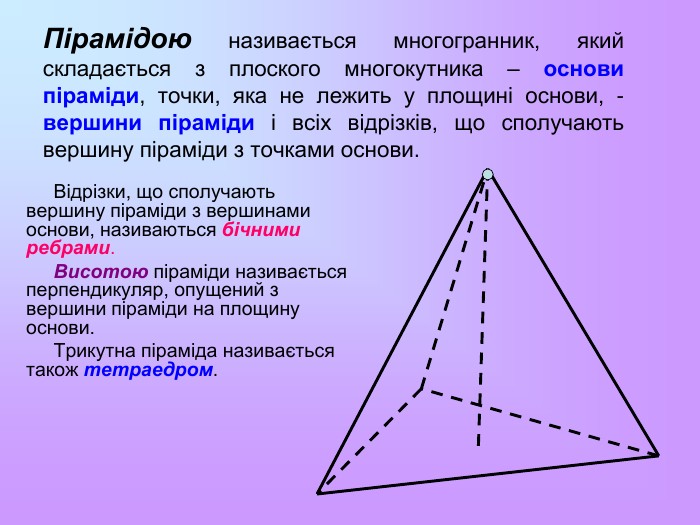
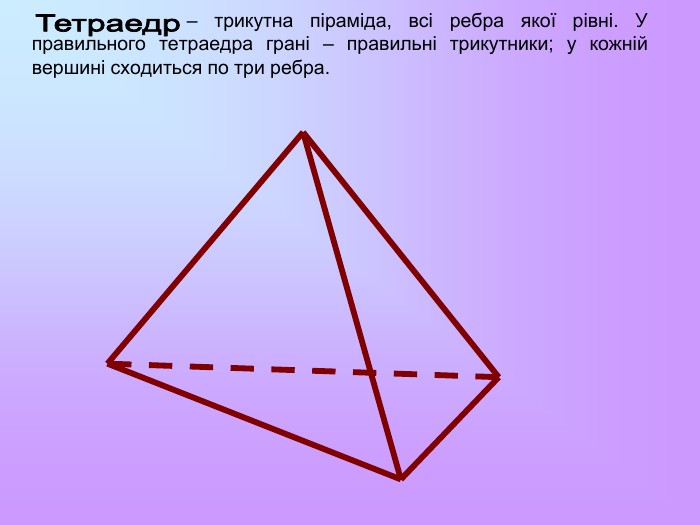
Пірамідою називається многогранник, який складається з плоского многокутника – основи піраміди, точки, яка не лежить у площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами. Висотою піраміди називається перпендикуляр, опущений з вершини піраміди на площину основи. Трикутна піраміда називається також тетраедром.

Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. Віссю правильної піраміди називається пряма, яка містить її висоту. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Оскільки у правильній піраміді бічні ребра рівні, то всі бічні грані – рівні рівнобедрені трикутники.

Побудуйте переріз піраміди SABC площиною, яка проходить через точки P,M,N, які лежать відповідно на ребрах AB, SB, AC. ПОБУДОВА

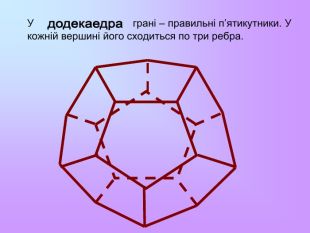
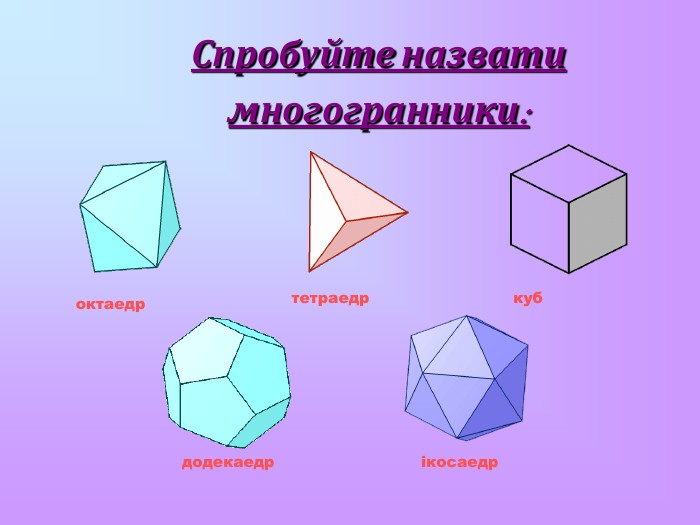
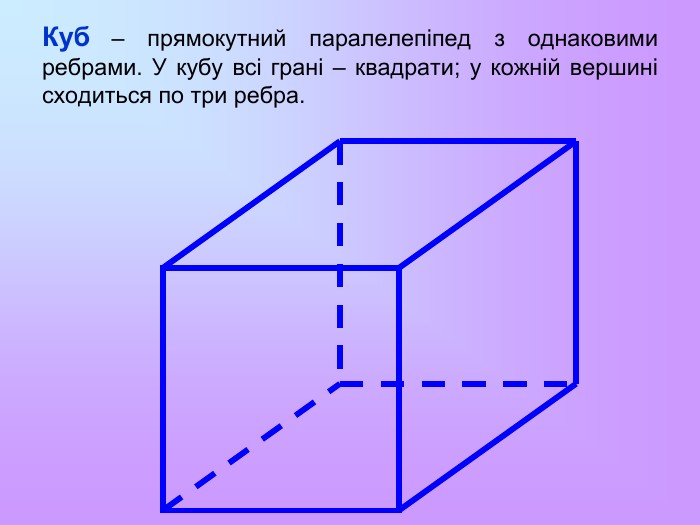
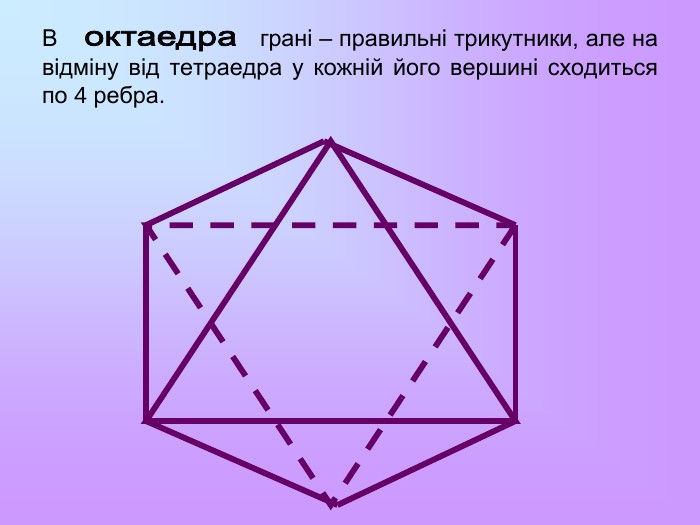
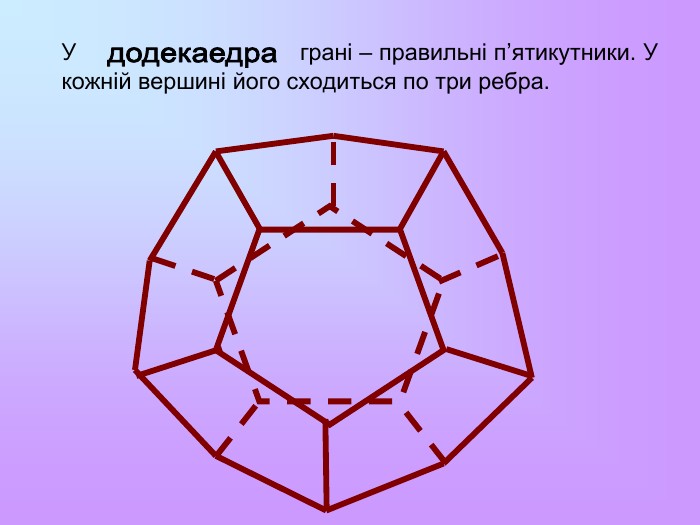
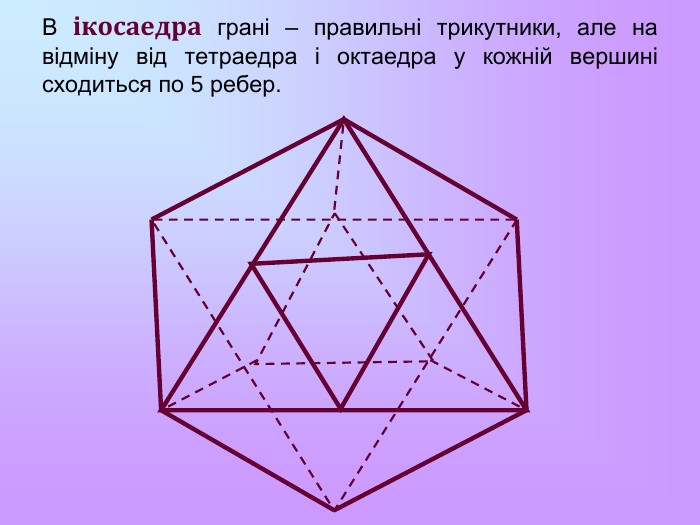
Многогранник називається правильним, якщо всі його грані – рівні правильні многокутники, а всі вершини рівновіддалені від деякої точки. Цю точку називають центром правильного многогранника. Існує 5 типів правильних опуклих многогранників: правильний тетраедр, куб, октаедр, додекаедр, ікосаедр. Назви тетраедр, гексаедр, октаедр, додекаедр, ікосаедр у перекладі з грецької означають чотиригранник, шестигранник, восьмигранник, дванадцятигранник, двадцятигранник відповідно.

Спробуйте назвати многогранники: тетраедр куб октаедр додекаедр ікосаедр

– трикутна піраміда, всі ребра якої рівні. У правильного тетраедра грані – правильні трикутники; у кожній вершині сходиться по три ребра.

Куб – прямокутний паралелепіпед з однаковими ребрами. У кубу всі грані – квадрати; у кожній вершині сходиться по три ребра.

В грані – правильні трикутники, але на відміну від тетраедра у кожній його вершині сходиться по 4 ребра.

У грані – правильні п’ятикутники. У кожній вершині його сходиться по три ребра.

В ікосаедра грані – правильні трикутники, але на відміну від тетраедра і октаедра у кожній вершині сходиться по 5 ребер.

Тип многогран ника Кількість ребер при вершині Кількість сторін грані Кількість граней Кількість ребер Кількість вершин Тетраедр 3 3 4 6 4 Октаедр 4 3 8 12 6 Ікосаедр 5 3 20 30 12 Гексаедр 3 4 6 12 8 Додекаедр 3 5 12 30 20

Коли Платон намагався знайти, якими ж повинні бути елементарні частинки землі, вогню, повітря, води й ефіру, допоміг йому в цьому молодий афінський математик Теетет. Завдяки його відкриттю Платон зміг дійти висновку. Ці 5 форм, не обов’язково в тому порядку повинні були, за Платоном, набувати елементарні частинки землі, води, повітря, вогню та ефіру: вогню – тетраедр, повітря – октаедр, землі – куб, води – ікосаедр, ефір – додекаедр. Призма. Прямокутна система побудови архітектурної форми була обумовлена статичною основою споруд, будівельними матеріалами, головним чином деревом, і найпростішим, що легко піддається вимірюванням, членуванням площини та простору. Людини створила собі світ прямокутних речей, видобуваючи із природи те, що може послугувати її потребам, - це результат діяльності людського розуму.

Рослин призматичної форми, практично, не існує. Ми знайшли лише один приклад. Басейн Нілу – край неосяжних боліт. Найбільш характерна рослина цих боліт – папірус. Папірус відомий як сировина, з якої в Давньому Єгипті виготовляли папір. Папірус має жорсткі тригранні стебла висотою до 4,5 м. І, звичайно, неможливо обійти розмову про шестигранну форму стільників у вуликах. Будова стільників дуже давно цікавила не лише математиків, а й інших вчених. Бджоли своєму житлу надавали такої форми, щоб за мінімальних витрат матеріалу та витрат часу побудувати найбільш простор приміщення і максимально раціонально використати невеликий простір вулика.

Царська гробниця Велика пираміда була збудована як гробниця Хуфу. Він був одним із фараонів, або царів стародавнього Египта, а його гробниця була завершена в 2580 році до н.е. Пізніше в Гізі було збудовано ще дві пирамиди, для сина і внука Хуфу, а також меньші за розмірами пирамиди для їх цариць. Піраміда Хуфу, найбільш віддалена на малюнку, є самою великою. Піраміда його сина знаходиться в середині і виглядає вищою, тому що стоїть на більш високому місці.

Абомінарет (від араб. – маяк), башта (кругла, багатогранна або квадратна в перерізі) для закликання мусульман на молитву. Розрізняють мінарети двох основних типів – 4-гранні (Північна Африка) або круглоствольні (Близький і Середній Схід).

Гірський кристаль (9см), знайдений на Уралі. Геологічні знахідки

Шеліт (5см), знайдений в Китаї.

Знаменитий художник, Альбрехт Дюрер (1471- 1528), в картині «Меланхолія» на передньому плані зобразив додекаедр.  

На картині художника Сальвадора Далі «Таємна Вечера» Христос зі своїми учнями зображені на фоні великого прозрачного додекаедра. .