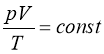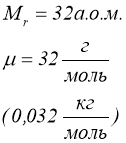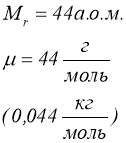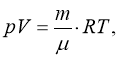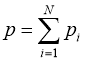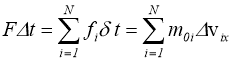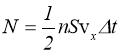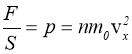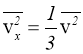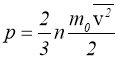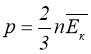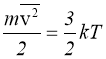1. МОЛЕКУЛЯРНО-КІНЕТИЧНА ТЕОРІЯ
ІДЕАЛЬНОГО ГАЗУ.

 

1.1. ПРЕДМЕТ І МЕТОДИ МОЛЕКУЛЯРНОЇ ФІЗИКИ.

 

Молекулярна фізика вивчає будову і властивості речовини та зміни її стану. При цьому вважають, що будь–яке тіло складається з великого числа частинок – молекул. Такі тіла називають макроскопічними. Методи вивчення властивостей макроскопічних тіл можуть бути різні.

Молекулярно – кінетична теорія (МКТ) розглядає тіло як сукупність великої кількості частинок – молекул, які хаотично рухаються і взаємодіють між собою. Вона пояснює властивості тіл, як сумарний результат дії молекул. МКТ застосовує до сукупності молекул математичні методи статистики, тому її називають також статистичною фізикою.

Другий метод – термодинаміка – вивчає макроскопічні властивості тіл, не цікавлячись їх мікроскопічною картиною. На основі дослідних даних формулюють основні закони, які називають принципами або началами термодинаміки. Ці закони і наслідки з них застосовують до конкретних фізичних явищ.

Термодинаміка і МКТ, розглядаючи зміни речовини з різних точок зору, взаємно доповнюють одна одну.

 

1.2. ОСНОВНІ ПОЛОЖЕННЯ МКТ ТА ЇХ ДОСЛІДНЕ ОБГРУНТУВАННЯ.

 

Існує три основних положення МКТ:

1. Всі тіла складаються з дуже маленьких окремих частинок – молекул, атомів, іонів.

2. Ці частинки перебувають в стані неперервного хаотичного руху.

3. Між частинками тіла одночасно діють сили взаємного притягання та взаємного відштовхування.

 

Атоми і молекули мають розміри порядку d ≈ 10^-8 – 10^-7 см. При визначенні розміру атомів часто використовують позасистемну одиницю довжини ангстрем: 1Ǻ=10^-8см.

Швидкість руху частинок пов’язана з температурою: чим більша швидкість, тим вища температура. Тому цей рух називають також тепловим. Таким чином, швидкість руху молекул визначає тепловий стан тіла – значення його внутрішньої енергії, яка дорівнює сумі кінетичної енергії молекул тіла та потенціальної енергії їх взаємодії. Взагалі до внутрішньої енергії входить і енергія частинок, з яких складається атом – електронів та ядер. Проте в молекулярній фізиці ця частина внутрішньої енергії не враховується.

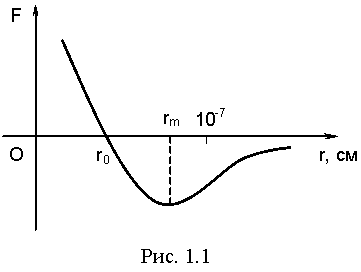Завдяки взаємодії між молекулами відбувається обмін енергією. Залежність сили взаємодії молекул від відстані між ними наведена на рис.1.1.

 

 

 

 

 

 

До непрямих доказів основних положень МКТ відносяться:

1. Значна здатність газів стискуватись свідчить про наявність великих відстаней між молекулами газу.

2. Газ намагається зайняти будь–який, як завгодно великий об’єм; це свідчить про те, що молекули газу рухаються незалежно одна від одної.

3. Взаємне проникнення газів, що дотикаються – дифузія газів – показує, що молекули одного газу рухаються в пустотах між молекулами іншого.

4. Змішування рідин, розчинення твердих тіл в рідинах також пояснюється перемішуванням молекул різних типів. При цьому об’єм суміші може відрізнятись від суми об’ємів речовин, що змішуються; це свідчить про різну компактність молекулярних систем. Наприклад, при змішуванні 100 см³ води і 100 см³ спирту, одержиться 196 см³ суміші; в суміші молекули розташовані компактніше, ніж раніш. До цього ж кола питань відноситься також явище випаровування рідин і твердих тіл.

5. Тиск газу на стінки посудини, в якій він міститься, пояснюється ударами молекул газу. Підвищення тиску при збільшенні густини газу пояснюється збільшенням числа молекул, що бомбардують стінки посудини. Збільшення тиску із збільшенням температури пояснюється зростанням швидкості молекул; це приводить до зростання частоти зіткнень молекул зі стінками посудини та до збільшення сили удару.

6. Рух щонайдрібніших твердих частинок, завислих у рідині чи газі – броунівський рух – пояснюється незрівноваженістю ударів, що їх зазнає броунівська частинка з боку молекул рідини чи газу. Так як розміри і маси молекул малі, то їх поштовхи можуть привести в рух лише дуже легенькі, броунівські частинки.

 

Чи можна побачити молекули?

Світло – це електромагнітна хвиля з довжиною 4000 – 7000 Å. Неозброєним оком можна бачити предмети розміром біля 1мм = 10 ⁷Å (діаметр голки). З допомогою лупи можна розглянути волосину – 10 ⁶ Å; В слабкий мікроскоп видно частинки диму – 10 ⁵ Å. Сильний мікроскоп дає можливість розглянути бактерії розміром від 10 ⁴  до 10 ³  Å. Деталі менших розмірів побачити в принципі неможливо. Рентгеноструктурний аналіз дав можливість вивчити кристалічні гратки твердих тіл. В електронний мікроскоп можна спостерігати органічні молекули (деталі до 4 Å ). Збільшення іонного проектора перевищує межу збільшення електронного мікроскопу в 3-4 рази, тому він дає можливість «бачити» навіть деякі деталі структури атома (розміри окремих атомів 2-4 Å ).

 

3. ІДЕАЛЬНИЙ ГАЗ. РІВНЯННЯ СТАНУ ІДЕАЛЬНОГО ГАЗУ.

 

Термодинамічною системою називають сукупність макроскопічних тіл. Система може складатись з одного або декількох тіл. Найпростішою системою є газ, обмежений деяким об’ємом. Стан системи характеризується величинами, які називають параметрами стану. До них належить тиск p, об’єм V і температура T.

Одиниці вимірювання:

[p] = Па;   [V] = м³;   [T] = К;   (Т = tºС + 273º)

1 Па = 1 Н/м²;   1 дин/см² = 0,1 Па;   1 бар = 10⁵ Па;

1 мм.рт.ст. 1 тор 133 Па;   1 ат = 1 кгс /см² = 0,98 бар;

1 атм = 1,01 бар (760 тор).

Рівняння, що зв’язує параметри стану, називають рівнянням стану.

Найпростіші властивості має газ, взаємодією між молекулами якого можна знехтувати. Такий газ називають ідеальним. При достатньому розрідженні всякий реальный газ близький до ідеального. 

Для розріджених газів емпірично були встановлені закони: Бойля–Маріотта, Гей–Люссака, Шарля. Тому ідеальним називають також газ, для якого точно виконуються ці закони.

Використовуючи газові закони, можна отримати зв’язок між p, V і T, тобто рівняння стану:

(1.1)

 

Для знаходження константи, яка залежить від маси і роду газу, введемо у розгляд кількість речовини і одиницю її вимірювання ­ моль.

Кількість речовини – це фізична величина, що вимірюється числом атомів чи молекул, з яких складається ця речовина. Одиницею вимірювання кількості речовини є моль. Моль – це така кількість речовини, яка містить стільки ж молекул, скільки атомів міститься в 12 г ізотопа вуглецю C¹².

Отже, за означенням, в одному молі різних речовин міститься одне і теж число молекул. Це число називають числом Авогадро :

N_A = 6,02 10²³ моль^–1.

Маса моля називається молярною масою .

Молярна маса виражена в грамах, чисельно дорівнює відносній молекулярній масі .

; ; ; ;

  

 

.

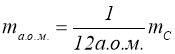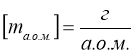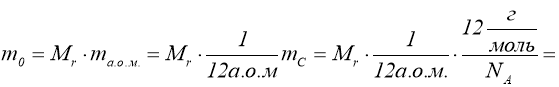
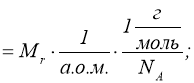
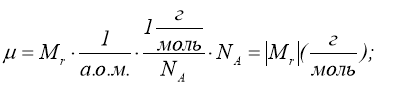
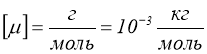О2

СО2

 

Згідно закону Авогадро молі усіх газів при однакових умовах займають однаковий об’єм. При нормальних умовах, тобто при р₀=760 тор = 10⁵ Па, Т₀=273 К (= 0º C) молярний об’єм дорівнює: V_0µ=22,4 л/моль = 22,4·10^-3 м³/моль.

Підставивши в (1.1) значення р₀, V_0µ , Т₀ знайдемо значення константи. Її називають універсальною газовою сталою R:

 

R=8,31 Дж/моль·К.

 

Отже, для одного моля рівняння стану ідеального газу має вид:

 

(1.2)

 

Для будь-якої маси m:

(1.3)

де 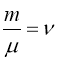- кількість речовини в молях.

Рівняння (1.3) називають рівнянням Клапейрона-Менделеєва. Число молей може бути представлено також і так: 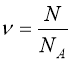, де N – число молекул в масі m. Підставивши останній вираз в (1.3) і виконавши перетворення, одержимо: ;

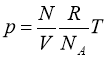Відношення 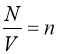- називається концентрацією молекул.

Відношення сталих 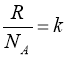- називається сталою Больцмана.

Одержуємо:

(1.4)

 

(1.4) як і (1.3) є рівнянням стану ідеального газу. Стала Больцмана k=1,38·10^-23 Дж/К. Із (1.4): 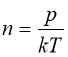; при однакових р, V і Т число молекул різних газів однакове.

Рівні об’єми різних газів містять при однаковому тиску і температурі однакове число молекул. Це твердження називають законом Авогадро.

При н. у. число молекул в 1 м³ газу позначають n₀ і називають числом Лошмідта: n₀ = 2,69·10²⁵ м^-3

Для суміші газів тиск суміші дорівнює сумі парціальних тисків її компонентів:

3 + ...

(1.5)

 

Рівняння (1.5) представляє собою закон Дальтона і може бути одержане з (1.4) і очевидного співвідношення  .

 

4. ОСНОВНЕ РІВНЯННЯ КІНЕТИЧНОЇ ТЕОРІЇ ГАЗІВ.

 

Тиск газу зумовлений тепловим рухом його молекул і виникає завдяки ударам молекул в стінки посудини. Одержимо зв’язок між тиском ідеального газу р і кінетичною енергією поступального руху його молекул, функцією якої повинен бути тиск. Нагадаємо, що тиском називається фізична величина, яка дорівнює відношенню нормальної складової сили до площі майданчика, на який вона діє:

 

 

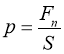
Для спрощення міркувань припустимо, що газ міститься в посудині, яка має форму паралелепіпеда, і перебуває в стані рівноваги. За один удар молекула передає стінці імпульс , де - час, протягом якого триває удар. Для знаходження середнього значення сили тиску проміжок часу треба взяти набагато більше, ніж час удару: » .

Виберемо систему координат, як показано на рис. 1.2, і обчислимо тиск на одну із стінок посудини; площа стінки дорівнює S. Сумарний імпульс

,

(1.6)

 

де N – число молекул, що долетять до стінки за час . Ці молекули розташовані від стінки на відстані , де - проекція швидкості молекули на вісь ОХ. Число молекул N дорівнює:

 

,

(1.7)

 

де n – концентрація молекул. Коефіцієнт ½ вказує на те, що тільки половина молекул летить в напрямі стінки S; друга половина молекул летить в зворотньому напрямі.

Зробимо ще два припущення, що спрощують розрахунки. 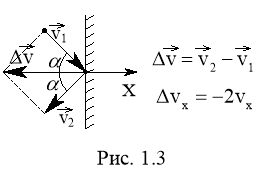Будемо вважати, по-перше, швидкості всіх молекул однаковими, і по-друге, удар молекул в стінку абсолютно пружним, тобто (див. рис. 1.3).

Враховуючи це, а також вираз (1.7), для імпульсу (1.6) одержимо:

 

,

 

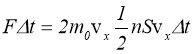звідки після перетворень матимемо:

 

(1.8)

 

Врахуємо  тепер  неоднаковість  швидкостей молекул і замість візьмемо середнє значення цієї величини . Потім, використавши очевидну рівність                            і умову повного безладдя молекулярного руху                              (всі напрямки рівноправні), одержимо:

(1.9)

 

Підставивши (1.9) у (1.8) і виділивши при цьому , маємо:

 

,    або

(1.10)

 

Тиск газу дорівнює двом третинам середньої кінетичної енергії молекул, що містяться в одиниці об’єму газу.

Вираз (1.10) називають  основним  рівнянням  кінетичної теорії ідеального газу.

Важливо підкреслити, що тиск газу визначається середньою кінетичною енергією його молекул. Це означає, що тиск газу - величина, органічно пов’язана з тим, що газ складається з великої кількості молекул.

Крім того, слід відмітити, що середнє значення квадрата швидкості потрібно відрізняти від квадрата середнього значення швидкості . Якщо , то не дорівнює . позначають або u і називають середньою квадратичною швидкістю молекул.

 

 

 

 

 

5. ТЕМПЕРАТУРА ТА ЇЇ ВИМІРЮВАННЯ.

 

З основного рівняння кінетичної теорії газів (1.10) випливає, що при незмінній концентрації молекул n (а, отже, при сталому об’ємі V) тиск газу залежить лише від кінетичної енергії його молекул. В той же час з досліду відомо, що при V = const тиск газу можна змінити лише нагріванням чи охолодженням. Тому можна вважати, що температура визначається середньою кінетичною енергією поступального руху молекул.

Для ідеального газу зручно вважати, що температура дорівнює:

,

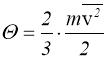тоді рівняння (1.10) набуде виду:

.

Одиницею вимірювання температури в цьому випадку буде Дж. Однак з ряду причин температуру прийнято вимірювати не в одиницях енергії, а в градусах. Коефіцієнтом, що переводить одиниці енергії в градуси, є стала Больцмана:

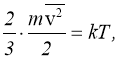
або:

(1.11)

 

Враховуючи (1.11), (1.10) можна подати так:

 

,

(1.12)

 

що співпадає з рівнянням стану ідеального газу в формі (1.4). Таким чином, теоретично одержане рівняння (1.10) дає змогу одержати всі закони ідеальних газів, що і являється критерієм його справедливості.

Перепишемо ще раз (1.11):

.

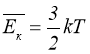Температура – це міра середньої кінетичної енергії поступального руху молекул.

Використовуючи поняття теплової рівноваги, температуру можна означити як величину, що характеризує стан теплової рівноваги: тіла, що перебувають в стані теплової рівноваги, мають однакову температуру і, навпаки, тіла з однаковою температурою перебувають в стані теплової рівноваги.

Вимірювання температури ґрунтується на законі, який стверджує, що якщо два тіла перебувають в стані теплової рівноваги з яким-небудь третім тілом, то обидва тіла перебувають в тепловій рівновазі й між собою.

Температура – не адитивна фізична величина.

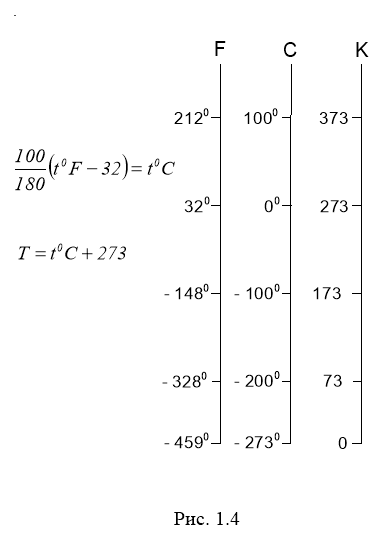Для вимірювання температури користуються тим, що при зміні температури тіла змінюються і його властивості (об’єм V, тиск p, електричний опір R і т.д.). Тому при створенні приладу для вимірювання температури, тобто термометра, вибирають термометричну речовину і визначають величини, що характеризують  його властивості (термометричні величини). Щоб встановити  одиницю вимірювання температури, користуються довільно вибраними реперними (опорними) точками (наприклад, температура танення льоду, температура кипіння води, тощо), яким приписують певні значення температури. На рис. 1.4 зображено найпоширеніші шкали Фаренгейта, Цельсія і Кельвіна.

 

 

 

 

 

 

 

 

Вимірювання об’єму газу.

 

Об’єм газу – це об’єм посудини, в якій газ перебуває. Найпростіше об’єм посудини виміряти, якщо заповнити його рідиною, густина якої відома (вода, ртуть). Зваживши посудину до і після заповнення, знайдемо об’єм:

 

.

 

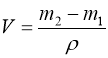При точних вимірюваннях необхідно враховувати теплове розширення і вносити поправки на температуру.

Якщо необхідно виміряти великий об’єм, то використовують волюмометр.

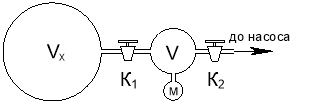До резервуару, об’єм V_x якого потрібно визначити, приєднують резервуар відомого об’єму V. Відкачавши обидва резервуара, перекривають кран К₁ і заповнюють об’єм V повітрям під тиском p₁. Кран К₂ закривають, К₁ відкривають і вимірюють тиск р₂. За законом Бойля-Маріотта:  p₁V=p₂(V+V_x),  звідки знаходять V_x .

 

Вимірювання тиску.

 

Прилади для вимірювання тиску називають манометрами. Якщо прилад призначений для вимірювання атмосферного тиску, то його називають барометром; дуже малі тиски вимірюють вакуумметрами. Діапазон тисків, що вимірюються, дорівнює 4·10⁵ атм – 10^-12 Тор. Для вимірювання тисків від 1 Тор до 1 атм використовують рідинні (переважно ртутні) манометри, для вимірювання високих тисків (до 10⁴атм) використовують манометр Бурдона.