Герун Ольга Валентинівна

 

 

 

Наочні задачі з фізикики в спеціалізованих

тестуючих програмах

 

 

 

Курсова робота

 

 

           

                                                                   

 

 

 

 

 

 

 

 

ЗМІСТ

 

Вступ………………………………………………………………………………….3

Розділ 1. Фізичнізадачі……………………………………………………………….………...5

1. Означення фізичної задачі…………………………………………………….5
2. Класифікація задач з фізики…………………………………………………..6
3.  Загальна послідовність розв^,язування задач……………………….………..8
4. Удосконалення підготовки вчителів до розв^,язування фізичних задач…………………………………………………………………………….9

Розділ 2. Наочні задачі з фізики………………………………………….………..13

   2.1 Засоби наочності у розв^,язуванні фізичних задач………………………….13

   2.2 Поняття про наочні задачі………………………………………….………..18

   2.3 Загальні зауваження до розв^,язування наочних задач……………………..20

Розділ 3. Наочні задачі з молекулярної фізики…………………………………..23

Висновки……………………………………………………………………………30

Список використаної літератури………………………………………………….32

Додатки……………………………………………………………………………..33

 

ВСТУП

 

Засвоїти курс фізики – це означає не тільки достатньо ясно і глибоко оволодіти системою знань, але й вміти застосовувати ці знання в навчальних цілях – для отримання нових знань – так і в практичному житті. Останнє  покладає оволодіння рядом практичних навиків: експериментальних, графічних, розрахункових, наочних і інших.

Навчити учнів розв^,язувати задачі з фізики – це не мета навчання. Розв^,язування задач – найпоширеніша і найбільш доступна форма перевірки практичних навичок учня. Але вчитель не завжди впевнений у тому, що учень розв^,язуючи задачу, розуміє її суть або добре бачить у житті те, про що йдеться в задачі. Адже деякі учні після розв^,язування текстової задачі не можуть накреслити до неї навіть схему або графік. При розв^,язуванні фізичної задачі бачити взаємозалежність явищ і співвідношень, покладених в її основу, набагато важливіше, ніж здобути її числові значення. Відповідь учень дістане, якщо усвідомить задачу.

Розв^,язування задач служить прекрасним методом розвитку мислення, самостійності в судженнях, наполегливості в подоланні труднощів.

Розв^,язування задач з успіхом використовується вчителями під час викладання нового матеріалу і його закріпленні, при проведенні фронтальних лабораторних робіт і особливо фізичних практикумів; задачі являються часто основним методом перевірки засвоєння знань з фізики.

У збірниках задач з фізики умови задач подаються у вигляді тексту і унаочнюються малюнками. В умові текстової задачі завжди дано готові значення величин і їх назви, а в підручнику – їх визначення і залежність у вигляді формул. Учні часто механічно підставляють дані у формулу і обчислюють їх. При цьому на обчислення затрачають часу в кілька разів більше, ніж на обдумування задачі.

Щоб розв^,язування задач було справді однією з форм закріплення знань і поглиблювало пізнання, треба поставити учня перед необхідністю вникнути в суть задачі. Така ситуація створюється, коли учневі пропонують задачу, умова якої викладена у вигляді фотографії, де відображено мить із самого життя.

Щоб розв^,язати таку задачу, треба чітко усвідомити які явища тут зв^,язані, проаналізувати ці явища. Цим пропонується учневі придивитися там, де він не звик дивитися, побачити те, що він не звик бачити раніше.

Отже, замість звичайної текстової задачі учневі пропонується фотографія явища – наочність для задачі. При цьому учень споглядає конкретне явище безпосередньо в процесі його перебігу. Наочні задачі не мають конкретно визначених даних, потрібних для їх розв’язання. Даються лише запитання, на які учень повинен відповісти.

Питання про вміння застосовувати знання на практиці є дуже актуальним. Однак навіть у випадку усвідомленого, не формального засвоєння навчального матеріалу, вміння застосовувати знання не приходить саме собою, цьому потрібно спеціально навчатись. При цьому розв’язування задач займає значне місце.

Моєю метою було розглянути наочні задачі, зокрема  наочні задачі з молекулярної фізики і особливості розв’язування їх.

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1

ФІЗИЧНІ ЗАДАЧІ

 

1.1 Означення фізичної задачі

Задача – це ситуація, яка вимагає  від суб’єкта деякої дії, яка скерована на знаходження невідомого   на основі використання його зв’язків із  відомим. (Г.  Костюк).

Задачі можуть бути навчальні, дидактичні, загальнопедагогічні, психологічні, соціальні, економічні тощо. В дидактиці оперують навчальними задачами. Така задача має своє специфічне призначення.

        Д. Ельконін називає навчальною задачею таку ситуацію, яка дозволяє людині, що її розв’язує, безпосередньо оволодіти відповідними процесами, способами, принципами або ”механізмом” виконання якихось практично значимих дій. Основне призначення навчальної задачі у засвоєнні самої дії, спямованої на оволодіння системою знань.

Методики викладання окремих предметів оперують різними визначеннями поняття “навчальна задача”. Одними з перших фізичну навчальну задачу визначили С. Каменецький і В. Орєхов: “Фізичною задачею в навчальній практиці звичайно називають невелику проблему, яка в загальному випадку розв’язується за допомогою логічних умовиводів, математичних дій та експерименту на основі законів і методів фізики. У методичній і навчальній літературі під задачами розуміють доцільно підібрані вправи, головне призначення яких полягає у вивченні фізичних явищ, формуванні понять, розвиткові логічного мислення учнів та прищеплення їм умінь застосувати свої знання на практиці”. У першій частині цього поняття “задача” визначається через поняття “проблема”. У ньому подаються засоби розв’язку. У другій частині – розкриваються дидактичні можливості фізичних задач. А. Усова і Н. Тулькібаєва підкреслюють, що фізична навчальна задача – це ситуація, яка вимагає від учнів мислительних і практичних дій на основі використання законів і методів фізики, спрямованих на розвиток в учнів фізичного мислення, оволодіння ними знаннями з фізики та уміннями використовувати ці знання на практиці. Задача для учнів є об’єктом вивчення, а для вчителя вона виступає методом навчання. Навчальна задача виконує різні функції: пізнавальну, виховну, розвиваючу, організуючу, контролюючу. Проте виконати всі названі фунуції разом може лише система задач. Більша частина задач зі шкільних збірників та підручників допомагають формувати в учнів фізичні поняття, знаходити взаємозв’язок між фізичними величинами, більш глибоко розуміти суть фізичних законів і явищ. Менше задач, розв’язок яких давав би можливісь розкрити механізм відповідних процесів та явищ.

Різноманітні функції задач визначають їх місце в навчальному процесі та можливості оволодіння учнями методами і способами їх розв’язання. Передумовою того є розуміння учнями суті задачі. Розуміння задачі визначається не тільки розкриттям його змісту, але й її структурою. Деякі автори (Ю. Кутамкін, А. Єсаулов) виділяють у структурі задачі два компоненти:

а) умову, тобто наявну сукупність об’єктів, які впорядковані відповідним чином;

б) вимогу, яка вказує на те, що потрібно шукати в даній задачі. Л.Фрідман у структурі задачі, крім умови та вимоги виділяє ще оператор. Під оператором задачі він розуміє сукупність тих дій (операцій), які потрібно виконати над умовою задачі, щоб реалізувати її вимоги.

Більш узагальнений підхід до питання про структуру задачі здійснений академіком В.Глушковим. Він у задачі виділяє задачну і розв’язуючу системи. До заданої  системи відносяться умова та вимоги задачі До розв’язуючої системи належать наукові методи, способи і засоби, які є передумовами створення конкретних алгоритмів для  розв’язування задач.

1.2 Класифікація задач з фізики

В методичній літературі задачі з фізики прийнято ділити на три види: текстові, експериментальні і графічні. Текстові і графічні задачі в свою чергу діляться на розрахункові і задачі-питанн або, як їх інакше називають, якісні задачі. В багатьох випадках розрахункові задачі поділяються на тренувальні і комбіновані. 

Задачі з фізики можуть класифікуватись за різними ознаками: за змістом, за дидактичною метою, за глибиною дослідження питання, за способом подання умови, за ступенем трудності, за глибиною дослідження питання.

Класифікація за змістом, наприклад, може бути такою: задачі з абстрактним і конкретним змістом. В абстрактних задачах виділяється й підкреслюється фізична суть явищ, відсутні несуттєві деталі. В конкретних задачах добре здійснюється наочність і зв’язок з життям. Задачі можуть бути також з політехнічним та історичним змістом. Якщо в задачах є матеріал, зв^’язаний з розвитком техніки, виробництва, сільського господарства, то їх називають задачами з політехнічним змістом. Коли ж задачі грунтуються на даних історичних дослідів, відкриттів тощо, то їх називають задачами з історичним змістом.

Можна виділити також цікаві задачі та задачі-парадокси.Такі задачі, як правило, містять незвичні, парадоксальні та цікаві факти або явища.

За способом подання умови задачі поділяються на текстові, експериментальні, графічні, задачі-малюнки.

За основним методом розв’язування задачі класифікують на якісні, обчислювальні, графічні та експериментальні. Але такий поділ не може бути строгим, бо у процесі розв’язування більшості задач використовують декілька способів.

Для якісних задач характерний аналіз фізичної суті явищ, які розглядаються в задачі.

В обчислювальних задачах відповіді на поставлені питання знаходять за допомогою обчислень і математичних операцій. Для розв’язування таких задач використовують арифметичнй, алгебраїчний і геометричний способи розв’язку. У процесі вивчення фізики в старших класах найбільш поширеним є  алгебраїчний та графічний способи. За характером логічних операцій під час  розв’язування обчислювальних задач розрізняють аналітичний і синтетичний методи.

При аналітичному способі розв^’язування задачі розпочинають з визначення шуканої величини. Але, як правило, у праву частину алгебраїчного виразу входять одне або кілька невідомих, які потрібно замінити іншими фізичними величинами, причому до того часу, поки всі величини, крім шуканої,  будуть відомі.

При синтетичному – послідовно знаходять зв^,язки між величинами, які задано в умові задачі. У систему таких зв^,язків повинна увійти шукана величина. При такому методі шукана частина проведених дій (кроків) може виявитись зайвою.

Найчастіше використовують аналітико-синтетичний підхід, у якому проявляються обидва ці методи.

Проте класифікація задач є досить умовною, оскільки неможливо чітко розділити, наприклад, розрахункові і якісні задачі – елемент тих і тих є в обох видах задач.

1.3 Загальна послідовність розв^,язування задач

У процесі  навчання учнів розв^,язуванню задач вчителі дотримуються певної послідовності етапів розв^,язування.

Одним з можливих варіантів є такий:

1. Читання умови задачі з поясненням термінів.
2. Пояснення фізичної суті задачі.
3. Короткий запис умови з переводом в єдину систему вимірювання фізичних величин (СІ, СГС).
4. Виконання малюнка відповідно до фізичної моделі задачі.
5. Складання плану розв^,язування.
6. Складання системи рівнянь (тобто математичної моделі задачі), розв^,язуючи яку, знайдемо відповідь на запитання задачі.
7. Розв^,язування задачі в загальному вигляді. Аналіз одержаної формули.
8. Знаходження числового значення шуканої величини та її розмірності.
9. Дослідження та аналіз відповіді.

      Така послідовність дає змогу привчити учнів та студентів до певного порядку під час аналізу та розв^,язування задачі. Крім того, слід зазначити, що така послідовність полегшує завдання викладача навчити учня розв^,язуванню фізичних задач. Додержуючи загальної послідовності, студенти і учні швидше уволодівають навичками й уміннями розв^,язування задач з даної теми. А якщо таку послідовність застосовувати для розв^,язування аналогічних задач з різних тем, то досягається досить глибоке засвоєння нового поняття, нового закону, способу розв^,язування.

1.4 Удосконалення підготовки вчителів до розв^,язування фізичних задач

    Аналіз стану викладання фізики показує, що в про­цесі навчання учнів розв'язувати задачі вчителі зазна­ють труднощів: вони добре їх розв'язують, але недо­статньо знають методику навчання учнів розв'язувати задачі.

    Змінити це, на нашу думку, можна, застосувавши інший підхід до навчання вчителів. Ефективною формою його реалізації є педагогічна гра. Суть її зводиться до того, що, змоделювавши потрібну діяльність і забезпе­чивши відпрацювання її головних компонентів у завдан­нях, які ставляться вчителям самої гри, ми досягаємо оволодіння ними відповідним видом діяльності, її ус­піх залежить від правильного вибору змісту і методів проведення гри.

    Покажемо, як у системі підвищення кваліфікації вчителів можна провести педагогічну гру з теми “Під­готовка вчителів до уроків з розв'язування фізичних задач”.

    М е т а  г р й: на основі врахування реальних можли­востей учнів спрямувати діяльність учителів на вибір диференційованих систем задач для навчання школярів та сформувати у них діяльність по проведенню уроків з розв'язування задач.

    Навчальним матеріалом для гри є методика розв'язу­вання фізичних задач, психологія застосування знань, класифікація відповідних уроків і методика їх прове­дення, форми організації пізнавальної діяльності учнів. Учасників гри на лекціях треба ознайомити з питан­нями, які є навчальним матеріалом.

    Щоб учасники гри свідомо і вільно оперували на­вчальним матеріалом, він повинен стати “предметом здій­снюючої дії”. Ця вимога реалізується в змісті гри і методах її проведення. Відомо, що вчителі часто виби­рають задачі для закріплення, повторення, системати­зації і узагальнення знань та їх контролю без урахуван­ня рівня підготовки учнів, що призводить до негативних наслідків. Учитель повинен знати, чим йому керуватись при підготовці до уроку з розв'язування задач. Саме цього повинна навчити вчителів гра. Крім того, її про­ведення сприятиме формуванню вмінь виявляти законо­мірності педагогічних явищ і діагностувати навчальну підготовку школярів, а також відпрацьовувати алгоритм дій з складання системи задач для учнів.

    Для проведення гри кожному учасникові видається розпорядження, яке інформує вчителя, що і як треба йому робити при підготовці до проведення різних уро­ків з розв'язування задач. Розпорядження містить вка­зівки:

    1.  Актуалізуйте  свої знання з таких  питань:

    —  фізичні задачі як засіб навчання і виховання,  їх місце в навчальному процесі;

    —  типи  задач, способи  і методи  їх  розв'язування;

    —  методика навчання розв'язуванню задач.

    2.  Запам'ятайте, що:

    —  в задачах мають бути реалізовані  принципи вихо­вуючого і розвиваючого навчання,  а  також  дидактичні принципи доступності, систематичності й послідовності;

    —  перед добором задач до уроку  треба   встановити, для якої мети, на відпрацювання яких понять і дій вони вам потрібні.

    3.  Встановіть, чи є у вас такі   задачі.   Якщо немає, то складіть їх самостійно.

    4.  Дослідіть  рівень навчальної  підготовки    уч­нів, рівень їх мотивації і наявність у них інтересу до навчальної діяльності.

    5.  Поставте    у    відповідність      реальні можливості  учнів   і дібрані  задачі.

     Крім того, кожному учасникові гри дається письмове розв'язання задач учнями одного з трьох сьомих класів на тему “Тиск твердих тіл” і пропонується завдання: про­аналізувати якість розв'язання ними задач і встано­вити рівень знань та вмінь цих учнів. Пропонується відповісти на запитання: Чим відрізняються знання і вміння учнів зазначених класів? У чому причина такої різниці? Від чого залежить рівень застосування знань? Які труднощі виникають в учнів під час засвоєння ними поняття тиску? Які шляхи подолання цих труднощів? Відповіді на запитання учасники гри записують у таку таблицю:

	Засвоюва- не поняття	Істотні ознаки засвоюва- них понять	Неістотні ознаки засвоюва- них понять	Передбаче- ні труднощі	Реальні труднощі учнів під час засвоєн- ня по­нять (7-А, 7-Б, 7-В кла­си)	Шляхи подолання усклад-нень

    Внаслідок індивідуальної роботи вчителів із записом ров'язання задач і таблицею вони переконуються в тому, що знання і вміння учнів у різних класах можуть бути різними, хоч методика проведення уроків була од­накова. Доходять висновку про необхідність врахуван­ня реальних можливостей учнів під час вибору мето­дики уроку — добору відповідних фізичних задач.

    Далі учасники гри мають дібрати систему задач, яка забезпечить засвоєння кожним учнем класу у повному обсязі поняття тиску.

     Колективне обговорення запропонованих варіантів таких систем для кожного класу допомагає виділити найдоцільніші з них.

    Так, учителі доходять висновку, що для учнів 7-А класу слід збільшити кількість задач на усвідомлення істотних ознак сили тиску, площі опори і самого поняття тиску. Кількість задач має бути такою, щоб учні могли засвоїти алгоритм їх розв'язання для будь-якого випадку.

    У 7-Б класі увагу учнів треба зосередити на засвоєнні істотної ознаки площі опори, розв'язуванні творчих задач та розвивати в учнів пізнавальний інтерес.

     Учням 7-В  класу треба створювати більші можли­вості для самостійної роботи, щоб вони грунтовно  за­своїли поняття тиску, а також давати, для розв'язання задані  творчого  характеру.    Закінчується гра демонструванням   змодельованих    уроків для   пропонованих класів. Ми розповіли про одну гру, присвячену виробленню основного уміння вчителя — правильно враховувати реальні можливості учнів для розв'язування фізичних задач.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2

НАОЧНІ ЗАДАЧІ З ФІЗИКИ

 

2.1 Засоби наочності у розв^,язуванні фізичних задач

   Навчити учнів розв’язувати задачі – одне із складних завдань викладання фізики. Аналіз стану викладання і успішності з фізики показує, що між теоретичними знаннями і практичними уміннями і навичками учнів існує певний розрив, зокрема між теоретичними знаннями і уміннями розв’язувати фізичні задачі.

До різних видів навчальної діяльності слід добирати відповідні типи задач. Важливо, щоб на уроці розв’язувалися задачі, які відрізняються особливим способом розв’язування, способом задання умови, змістом тощо. Це дає змогу актуалізувати пізнавальну діяльність учнів у процесі розв’язування задач. Тому до уроку розв’язування задач слід добирати якісні, розрахункові, графічні, експериментальні, творчі задачі в їх органічній єдності. Це дає можливість поступово ускладнювати зв’язки між величинами і поняттями, які характеризують процеси або явища, що описуються в задачах. Правильний добір задач робить урок змістовнішим і цікавішим. Крім того вчитель повинен використовувати ряд засобів і прийомів для активізації пізнавальної діяльності учнів на всіх етапах роботи над задачами. До них можна вінести: висунення гіпотез і пропозицій, які спямовані на пошуки способів розв’язування задачі, створення атмосфери дискусії в класі; вказівки на практичне значення задач; використання фрагментів телевізійних передач, кінофрагментів, діапозитивів, транспарантів до графопроектора, фотографій, малюнків, графіків, схем, креслень, приладів і установок тощо; аналіз спостережень, експериментальних задач; використання науково-популярної, довідкової та художньої літератури.

Розв’язування задач – це активний пізнавальний процес, велику роль у якому відіграють спостереження фізичних об’єктів і експеримент. Вони сприяють створенню відповідних образів і уявлень, уточненню умови задачі, одержанню даних, яких не вистачає, встановленню залежності між фізичними величинами, що характеризують процес або явище, яке розглядається в задачі.

Будь-яка задача з фізики, крім тренувальної, несе для учнів певну інформацію. Ана­лізуючи умову задачі, необхідно добиватися, шоб учні розуміли і уявляли собі все те, про що йдеться в умові. Цьому, без­перечно, сприятимуть засоби наочності.

Під засобами наочності ро­зуміють різноманітні засоби, за допомогою яких конкрети­зується і з'ясовується зміст за­дачі, способи і прийоми її розв'язування. Такими засо­бами можуть бути малюнки, схеми, фотографії, діаграми, шкали, карти, моделі устано­вок і приладів, діапозитиви, кодотранспаранти, експери­ментальна перевірка розв'яз­ку.

Використання малюнків, креслень чи схем, з одного бо­ку, є обов'язковою умовою успішного аналізу фізичних за­дач. Одним з недоліків у ро­ботах учнів є відсутність на­званих више засобів наочності. З іншого боку, вибір способу розв'язування задачі залежить від її формулювання і наочно­го оформлення. Встановлено, що залежно від співвідношен­ня наочного оформлення і словесного формулювання розрізняють два способи розв'язування задач: пряме роз­в'язування з відповідно сфор­мульованою вимогою і опосе­редковане — розв'язування за допомогою переосмислення і видозміни наочного оформлен­ня задачі. Під час переосмис­лення відбувається зміна об'єк­та діяльності. Учні, аналізу­ючи нове креслення чи малюнок, виявляють у ньому нові властивості, що допомагає їм знайти правильні шляхи роз­в'язання задачі.

У процесі аналізу задачі, до­бираючи відповідне наочне оформлення, увагу учнів слід акцентувати на тому чи іншо­му способі розв'язування. Цей прийом є корисним саме для задач на оволодіння способа­ми діяльності у тих випадках, коли вчитель демонструє їх уч­ням, а також коли учні самостійно шукають нових спо­собів діяльності.

Практика показує, шо біль­шість учителів приділяє знач­ну увагу засобам наочності під час розв'язування задач. Але не всі типи і види засобів наочності використовуються для постановки і розв'язування за­дач; мало використовуються графіки, фотографії, практич­но зовсім не використовують­ся діаграми, шкали, карти.

Які ж можливості засобів наочності для постановки і розв'язування задач?

       1. Малюнки можуть відігра­вати різну роль під час розв'язу­вання задач: а) як засіб пере­осмислення задачі; б) малюн­ком можна задати умову задачі; в) вимірюючи певні еле­менти малюнка, можна визна­чити шукану величину.

Учні краще розуміють ло­гічний аналіз умови задачі, ко­ли на дошці, екрані або в зо­шитах малюнок виникає по­ступово, а поява кожного еле­мента малюнка супроводжу­ється поясненням учителя. У даному разі слово поєднуєть­ся з певними наочними обра­зами, що полегшує формуван­ня поняття про фізичні про­цеси, взаємозв'язки між ве­личинами, про принципи дії приладів. Якщо малюнок про­понується в завершеному ви­гляді, то він є таким само складним комплексом взає­мозв'язаних характеристик фізичного процесу або явища, про які йдеться в умові задачі. У цьому разі він дає значно менший ефект для розвитку мислення учнів.

       Під час використання малюнків як засобу переосмис­лення задачі можна простежи­ти деякі відмінності їх призна­чення: а) малюнок дає уявлення про певне фізичне яви­ще і визначає хід розв'язуван­ня задачі; б) за допомогою ма­люнка схематично зображають процес і тіла, задані в умові задачі; в) за допомогою ма­люнка конкретизується умова задачі.

      Задачі, умови яких задають­ся за допомогою малюнків, характеризуються тим, що всю інформацію, необхідну для їх розв'язування, учні знаходять самостійно, аналізуючи зоб­ражену ситуацію. Вони за ма­люнком визначають коло ви­хідних даних, шукають мож­ливі шляхи розв'язання задачі. При цьому учні вчаться не просто встановлювати від­повідності між вихідними ве­личинами і літерною сим­волікою формул, а пізнають фізичний зміст розглядуваних явищ і законів, ознайомлю­ються з діючими системами одиниць, їх співвідношення­ми і перетвореннями.

     Щоб розв'язування задач було справді однією із форм засвоєння знань і поглиблю­вало пізнання, треба постави­ти учня перед необхідністю вникати в суть задачі. Така си­туація створюється, коли уч­неві пропонують задачу, умо­ва якої подана у вигляді фо­тографії, де відображено мить із самого життя.

 2. Фотографії як засіб на­очності можуть бути таких видів:  а)фотографії шкал за­собів вимірювання, які вико­ристовуються в задачах для заміни значень величин. Ці значення учень бере із фото­графій засобів вимірювання; б) фотографії фізичних об'єктів, якими можуть бути предмет, механізм, явище (фотографія рухомого автомобіля чи дви­гуна внутрішнього згоряння). У таких випадках треба врахо­вувати масштаб фотографії; в)фотографії як результат ек­сперименту. Такі фотографії, в основному, називають фотодокументальним матеріалом, яким можуть бути: стробо­скопічні фотографії, серії знім­ків явищ у різний час, при швидкісній кінозйомці, фо­тографії осцилограм, треків, спектрів, мікрофотографії, рентгенограми.

     У цьому разі дії учня ана­логічні до тих, коли йому до­водиться розв'язувати задачу, умова якої задана малюнком.

    3. Графіки під час розв'язу­вання задач призначені для:

    а) визначення фізичних вели­чин, значення яких за табли­цями знаходити незручно, а обчислити за формулами учні не можуть;

    б) наочного зображення суті фізичних процесів, які харак­теризуються відповідними фі­зичними величинами, що пе­ребувають між собою у певній функціональній залежності.

 Крім того, значну увагу треба приділяти розв'язу­ванню задач на побудову гра­фіків, що сприятиме розумінню учнями залежності між фізич­ними величинами.

    4. Схеми поділяються на кінематичні, гідравлічні, пнев­матичні, оптичні, електричні. У розділах "Енергія.  Робота і потужність", "Тиск твердих тіл, рідин і газів", "Теплові двигу­ни" та інших розглядаються бу­дова і принцип дії різних ме­ханізмів,  їх малюнки є кіне­матичними схемами.  Тому, вивчивши будову і принцип дії барометра-анероїда, маномет­ра, привода поршневих гід­равлічних насосів і гідравлічно­го преса, гідравлічного і пнев­матичного гальм автомобілів, важелів, можна запропонува­ти учням розв'язати ряд задач.

    До схем належать і гео­графічні карти.

    5.  Географічна карта — це наочний образ, що дає змогу охопити явище у всій його цілісності і складності, з усіма закономірними і випадкови­ми деталями. Використовую­чи карти, можна поставити за­дачі з механіки, електроди­наміки, гідростатики тощо.

Аналіз різних збірників за­дач з фізики показав, шо в них відсутні задачі з використан­ням діаграм і шкал.

    6. Діаграми дають учням на­очне уявлення про співвідно­шення фізичних величин, а та­кож сприяють легшому за­пам'ятовуванню багатьох з них. Можна використовувати діагра­ми різних типів: з об'ємним зображенням величини,  стовп­часті,   лінійні, кругові  та ін. Щоб   легше  розрізняти  тіла

(реновини, величини), на діагра­мах використовують штриховку і колір.

 Розв'язування задач з вико­ристанням діаграм привчає учнів порівнювати фізичні ве­личини, співвідносити їх з іншими.

    7. Шкали — прямі лінії, на яких нанесено звичайний або логарифмічний масштаб, вибра­ний для зображення будь-яких фізичних величин. На прямій відмічають точки, що відповіда­ють числовим даним зображе­них величин, і навпроти цих точок виконують малюнки і по­яснювальні написи.

Розв'язування задач з вико­ристанням шкал сприяє ознайомленню учнів з різними зна­ченнями фізичних величин і легшому їх запам'ятовуванню.

    8. Цінними засобами уна­очнення під час розв'язуван­ня задач є демонстрування дослідів, приладів, установок, моделей, деталей машин.

      Для розв'язування задач не­обхідно використовувати інфор­мацію, одержану під час де­монстрацій на інших уроках, у процесі виконання лабора­торних робіт, на екскурсіях. Це дає змогу спиратися на кон­кретні фізичні явища або про­цеси, "матеріалізувати" умову розглядуваної задачі. Але ма­теріал спостережень не може повністю замінити спеціальні демонстрації, призначені для ілюстрації умови задачі, тому що будь-яка безпосередня де­монстрація більше конкрети­зує умову задачі, ніж відтво­рювані образи попередніх спос­тережень.

    Під час розв'язування за­дач досліди можна використо­вувати на різних етапах роз­в'язання задачі для:

    ознайомлення учнів з фізич­ним явищем. Увага звертаєть­ся не на кількісні характеристики явища, а на його відтво­рення;

    перевірки результатів, одер­жаних у процесі розв'язуван­ня задачі.                     Практика показує, що така ілюстрація найдо­цільніша, бо учні ознайомлю­ються не лише з якісним бо­ком явища, а й перевіряють кількісні його характеристи­ки. При цьому слід уникати таких задач, де можлива знач­на розбіжність між обчисленим і виміряним значеннями фізичної    величини.

    Таким чином, використан­ня засобів наочності під час розв'язування фізичних задач, що подаються у цілісній сис­темі, дає змогу учням не ли­ше активно і планомірно ово­лодівати фізичними знання­ми, а й набувати навичок ви­користовувати ці знання твор­чо. Це виявляється в умінні аналізувати задачу, видозміню­вати задачну ситуацію з метою пристосування її до іншого ме­тоду розв'язування, знаходи­ти нові прийоми і способи, ви­являти і нагромаджувати нову інформацію, досліджувати здо­буті результати.

2.2 Поняття про наочні задачі

За останні роки на уроках фізики став широко застосовуватись роздатковий матеріал. Частина  його випускається видавництвами, частина виготовляється вчителями самостійно.

За принципом  побудови  цей  матеріал  може бути розділений на два типи: 1) традиційні, тобто текстові, які за формою і змістом повторюють задачі із задачників, але тільки виконані на окремих карточках;  і  2) такі, в яких вся інформація, необхідна для розв^,язку задачі, представлена на малюнку ( задачі цього типу називають наочними ).

Дидактичні матеріали першого типу, безумовно, корисні, тому що вони дозволяють здійснити більш диференційований підхід до учнів в процесі організації вправ і закріплення пройденого. Однак в них вихідні величини задані, як правило, в готовому вигляді. Тому діяльність учнів зводиться в основному до відшукання відповідності між даними задачі і відомими їм формулами, внаслідок чого задачі цього типу мало допомагають формуванню умінь самостійно знаходити вихідні дані.

Виконання завдань з дидактичного матеріалу другого типу – це вправи, які допомагають переносу знань в область практики; за ціллю і змістом вони близькі до практичних задач.

При складанні дидактичних карток прийнято наступні поняття:

1. Необхідні похідні дані для вправ беруть із рисунка на карточці.
2. Рисунок на карточці допомагає розвитку і виробленню навиків відліку по шкалах вимірювальних пристроїв чи по графічних зображеннях залежностей між величинами.

 З метою систематичного повторення раніше пройденого матеріалу на основі нового кожна карточка охоплює декілька тем програми.

3. Питання до кожного набору карточок для всіх учнів класу одинакові, щоб постановка їх не затрудняла вчителя. Відповіді на кожне питання і для кожного номера карточки є у вчителя, полегшуючи тим керування учнів і швидку перевірку отриманих відповідей.

         4. Картки  забезпечують самостійну роботу кожного учня.

       5.Картки дають можливість проводити по них програмоване навчання, як машинне, так і безмашинне.

       6. Картки не заміняють собою самостійну роботу учнів з пристроями на лабораторних заняттях.

При традиційній методиці формування практичних умінь і навиків переважають дії з матеріальними об^,єктами, реальними приладами і облаштуванням – це добре, тому що лабораторні роботи завжди виконуються двома учнями. Кількість лабораторних вправ недостатня для того, щоб забезпечити формування деяких, найбільш складних умінь у всіх учнів. Робота з розглядуваним дидактичним матеріалом не заміняє практичні і лабораторні роботи, а повинна їх випереджати.

Наочні задачі ( як і звичайні ) можуть бути декількох видів: якісні і кількісні, тренуючі і творчі. Однак наочні задачі, на відміну від текстових, більшою мірою допомагають формуванню в учнів інтелектуальних частин практичних навиків.

Малюнки повинні бути максимально спрощеними чи схематизованими. Ступінь схематизації з плином часу може збільшуватись.

Малюнки за своєю природою статичні. В багатьох випадках потрібно відобразити динаміку процесу чи різні його етапи. В цьому випадку приходиться застосовувати умовні прийоми, і з ними теж потрібно знайомити учнів. Строгих правил для надання малюнку динамічності не існує. Все залежить від винахідливості і смаку його автора, однак потрібно прагнути до деякої однотипності прийомів, що допоможе учням їх засвоїти.

Вимоги до тексту можна сформулювати наступним чином:

1. умова не повинна містити числових значень фізичних величин; виняток складають табличні дані, фізичні константи  і величини, які важко просто і наочно зобразити;
2. при необхідності текст може містити пояснення ситуації, яка зображена;
3. текст повинен дапомагати виробленню алгоритму розв^,язання задач даного типу, тому умову задачі бажано представити у вигляді послідовних логічних доз;

Задачі з використанням наочності не мають конкретно визначених даних, потрібних для її розв^,язання. Даються лише запитання, на які учень повинен дати відповідь.

2.3 Загальні зауваження до розв^,язування наочних задач

П л а н  р о з ^, я з у в а н н я  з а д а ч:

1. Глибоко проаналізувати задачу, щоб чітко усвідомити, що і як робити.
2. Визначити лінійні розмірі потрібних частин приладу або установки.

У деяких випадках деякі дані подаються в готовому виглядіі (вага тіла,      гутина тощо).

3. Записати в зошит дані для розв^,язування задачі у відповідній  системі за встановленою формулою, як і при розв^,язуванні текстової задачі. Якщо задачу    розв^,язують у системі СІ, то треба перевести одиниці вимірювання у цю систему.
4. Розв^,язати задачу в загальному вигляді, дістати розмірності відповідей.

Знайти числове значення відповідей.

5. Проаналізувати відповіді і знайти їх вірогідність.

            Задачі підбираються так, що, розв^,язуючи їх учень спостерігає перебіг явищ, бачить взаємозалежність явищ, які покладені в основу задачі. Розв^,язувати  задачі слід у тій послідовності, в якій подано завдання до фотографії. До кожної задачі даються запитання, відповіді на які учень повинен дати, користуючись малюнком (чи фотографією). Як, правило, завдання дають у порядку зростання їх складності.

Якщо використання наочності при розв^,язуванні задач занесене в систему, то з цих задач можна починати перевірку домашнього завдання. На будь-якому уроці паралельно з усним чи письмовим опитуванням можна запропонувати учням розв^,язати задачу з використанням наочності. При цьому учням іноді треба дати папір, масштабну лінійку і фотографію з теми минулих уроків. Після ознайомлення з фотографією учень повинен, наприклад, пояснити, що зображено на фотографії, проаналізувати те, що бачить, дати визначення, з^,ясувати принцип дії приладу, зробити найпростіші обчислення, сформулювати закон, який лежить в основі цих явищ, відображених на фотографії, відповісти на інші запропоновані вчителем запитання. У протилежному випадку фотографія є тим завданням (або його частиною), яке вчитель хоче поставити перед учнем.

Фотографію можна використати в процесі пояснення нового матеріалу. Під час пояснення нового матеріалу вчитель роздає фотографії із спеціального набору, що є в нього, або із збірника задач. Щоб закріпити вивчений матеріал, учитель пропонує учням за фотографіями виконати нескладні обчислення або усно дати висновки з теми, що вивчається.

Задачі з використанням наочності можна пропонувати на самостійні або контрольні роботи. Їх можна використовувати і під час повторення матеріалу. Це можна зробити по-різному. Наприклад, можна зробити огляд теми за допомогою діафільму задач або у вигляді окремих фотографій на паперовій стрічці для епідаскопа, де одночасно аналізується задача і ставиться завдання для всього класу.

Задачі з використанням наочності можна застосовувати як запитання під час заліків з окремих тем. При цьому запитання у вигляді фотографій, а також текстові запитання вивішують на видному місці за кілька днів перед заліками.

Задачі з використанням наочності можна давати як домашнє завдання (краще після закінчення теми). У домашніх умовах учень, розібравшись у задачі, розв^,яже її краще, з поясненням. Такі домашні роботи можна давати на тривалий час. Їх виконують як звичайне розв^,язування задачі (з поясненням) або у формі твору з фізики, темою якого є той комплекс явищ, що його відображує фотографія. Завдання, що даються додому, можуть мати поурочний характер, тематичний або характер огляду ряду тем.

Задачам з використанням наочності серед різних видів задач належить особливе місце. Вони мають дослідницікий характер. Очевидно ця особливість робить їх “більш фізичними”: у них на перший план висувається аналіз явищ, а не використання математичних засобів для розв^,язування.

Готуючи дані для розв^,язування задачі, учень бачить, що явища в природі не існують окремо, розділено, вони взаємозв^,язані, взаємообумовлюються одне з одним. Найменша зміна однієї величини зумовлює зміну, а то й зникнення або появу іншої.

Перевагою задач такого типу порівняно з експериментальними задачами є також те, що їх можна розв^,язувати фронтально, оскільки фотографії можна розмножити в будь-якій кількості.

РОЗДІЛ 3

 

НАОЧНІ ЗАДАЧІ З МОЛЕКУЛЯРНОЇ ФІЗИКИ

   

       В шкільному куцрсі фізики учні вивчають різні її розділи. Зокрема вивчають важливий розділ – молекулярна фізика, яка розглядає будову і властивості речовин в твердому, рідкому й газоподібному станах і залежність фізичних властивостей тіл від їх будови та особливостей молекулярного руху. Стосовно будови і властивостей речовин молекулярна фізика виходить з так званих молекулярно-кінетичних уявлень. Згідно з цими уявленнями будь-яке тіло – тверде, рідке чи газоподібне – складається з величезної кількості молекул, що перебувають у невпорядкованому (хаотичному) русі, інтенсивність якого залежить від температури.

       При вивченні в середній школі основ молекулярно-кі­нетичної теорії  розв'язуються   задачі таких трьох типів:

    1)  на засвоєння основних положень молекулярно-кіне­тичної теорії, експериментальних фактів та явищ, що її обґрунтовують, і на формування конкретних уявлень про розміри молекул, їх швидкості, величину їх мас, про число молекул в  грам-молекулі   речовини тощо та про способи визначення цих величин;

    2)  на   застосування    основного   рівняння   кінетичної теорії;

    3)  на застосування рівняння стану газу в загальному випадку і для часткових випадків.

    При розв'язуванні задач, особливо перших двох типів, важливо мати  на   увазі   спрощення, які   часто   застосовуються при вивченні основ молекулярно-кінетичної тео­рії. До таких спрощень належать: 1) замість розгляду справжнього розподілу молекул за складовими їх швидко­стей припускають, що молекули газу рухаються в трьох взаємно перпендикулярних напрямах. Внаслідок однакової ймовірності будь-якого напряму для швидкості молекули припускають, що по-кожному з трьох взаємно перпенди­кулярних напрямів рухається третина всіх молекул; 2)справжній розподіл молекул за числовим значенням швидкості часто замінюють припущенням про рівність швидкостей всіх молекул за числовим значенням; 3) при розгляді ударів молекул об площадку справжню кількість ударів замінюють середньою.

 Ефективнісь практичних занять з розв’зування фізичних задач значно зростає, якщо учнів навчати, як саме треба розв’язувати задачі того чи іншого типу.  Використовуючи той чи інший метод під час розв’язування відповідної задачі, учні стають ніби дослідниками, відкривачами нових явищ, починають працювати творчо, з натхненням, з цікавістю.

Дуже ефективним для розвитку розумової діяльності учнів є використання додаткового дидактичного матеріалу з фізики.

Дидактичний матеріали з молекулярної фізики  багатьох авторів був випущений у вигляді карток-завдань для різних класів. Так, в посібнику Скреліна Л. І. Можна розглянути набір дидактичних карток для самостійної роботи учнів 10 класу на уроках фізики. Запропонований набір дидактичних карток складається з 12 серій, по 12 карток в кожній серії. З них 10 карток основні й дві доповнюючі. На карточках викладено умову задачі не в формі тексту, а у вигляді малюнка. До кожної задачі потрібно давати 12 запитань,  в зв’язку з існуючою дванадцятибальною системою оцінювання в школі. Завдання є неважкі, тому за кожну правильну відповідь на одне питання, учень отримує по 1 балу. Відповіді на ці питання учень повинен дати, користуючись малюнком. Ці задачі можна використовувати при перевірці знань учнів з конкретної теми.

Для забезпечення кращого контакту між учнями і вчителями під час роботи рекомендується повісити плакат із збільшеним зображенням малюнка якоїсь карточки з даної серії. Щоб учні краще сприймали малюнок карточки, корисно на демонстаційному столі зібрати установку, яка відповідає тій, що зображена на дидактичних картках даної серії.

Ми розглянули три серії карток з цього дидактичного матеріалу. Опишемо коротко кожну з них.

 

1 Серія  - тиск повітря і пари

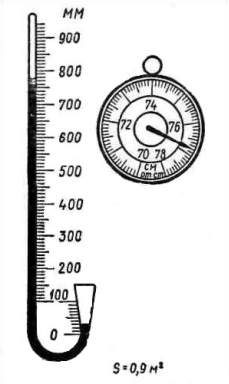
На правому малюнку карточки зображений барометр-анероїд, який показує істинний атмосферний тиск, на лівому – барометрична труба з ртуттю, в яку після отримання вакууму впустили деяку кількість води. Частина цієї води утворила над ртуттю насичену водяну пару. Про існування цієї пари можна судити з того, що деяка кількість води знаходиться над поверхнею ртуті і  за відповідним зниженням рівня ртуті внаслідок тиску водяної пари.

 Нариклад для карточки № 6 відповіді учня будуть виглядати так:

1. Ціна поділки шкали барометра-анероїда – 1 мм рт. ст.
2. Нижня межа вимірювання тиску барометром-анероїдом – 730 мм рт. ст.
3. Верхня межа вимірювання тиску барометром-анероїдом - 780 мм рт. ст.
4. Атмосферний тиск повітря за цим барометром в мм – 768 мм рт. ст.
5. Атмосферний тиск повітря в ат. –  1,007 ат.
6. Сила тиску атмосфери на площину – 0,9 м², рахуючи 1 мм рт. ст. =133 Па:          F = 133 Па ∙768 ∙0,9м² = 91929 н = 92 кн.
7. Різниця гідростатичних тисків стовпчиків ртуті в барометричній трубі – 730 мм рт. ст.
8. Тиск насиченої водяної пари над ртуттю.

             P_{нас. пари}  = 768 мм рт. ст. – 730 мм рт.            ст. = 38 мм рт. ст.

9. Температура цієї пари і навколишнього атмосферного повітря (знах. за табл. чи плак.) 33 ^оС.
10. Тиск водяної пари в повітрі:

Р_{вод. пари} = 38 мм рт. ст. ·0,5 = 19 мм рт. ст.

11. Тиск сухого повітря.

      Р_{сух. пов.} = 768 мм рт. ст. – 19 мм рт. ст. = 749 мм рт. ст.

12. Точка роси = -21 ^оС.

Для відповіді на питання 6 і 9 треба використати таблицю тиску насиченої водяної пари чи плакати, на яких зображена залежність тиску цієї пари від температури.

2 Серія – вимірювання тиску газу манометрами

На кожній карточці 2 серії  зображені дві посудини, з’єднані між собою в нижній частині трубкою з краном. Рідинний ртутний манометр вказує тиск газу в лівій посудині, а металевий манометр – тиск в правій посудині.

На більшості карток зображені відкриті рідинні манометри, які показують різницю між тиском газу в посудині і тиском навколишнього атмосферного повітря. Цей останній тиск прийнято за одну атмосферу і при обчисленнях приймається рівним Па (паскаль).

На карточках № 8, 10 і 12 показані закриті манометри. Вони відразу дають величину тиску в посудині незалежно від зовнішнього атмосферного тиску.

Металеві манометри, якими вимірюється тиск газу в правому манометрі, теж поділяються на два типи:  “атu” і “ата”. Надпис над манометром “атu” (карточки № 1, 2, 3, 5, 6, 9, 11) умовно означають “надлишковий тиск”, тобто величину, на яку тиск повітря в посудині перевищує атмосферний тиск. Надпис “ата” (карточки № 4, 7, 8, 10, 12) вказують істинне значення тиску газу ( абсолютний) без врахування зовнішнього атмосферного тиску.

 Тиск на металевих манометрах вимірюється в технічних атмосферах (ат) : 1 ат = 1 кгс/см = 9,81·10⁵ Па, для спрощення розрахунків рекомендується заокруглити до 100 000 Па (10⁵ Па). З цією ж метою рекомендується тиск 1 мм рт. ст. = 133,322 Па заокруглити до 133 Па.

Температуру, при якій знаходяться два гази в посудинах, рахувати рівною 27ºС.

Наприклад, для карточки № 5 відповіді учня будуть виглядати так:

 

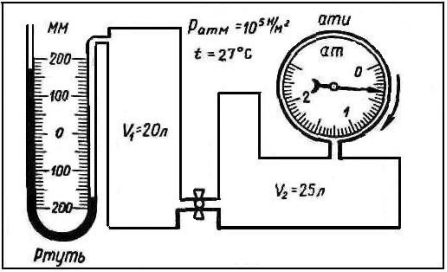
Рис. 3.2. Приклад карточки 2 серії (№ 5)

1. Ціна поділки шкали рідинного манометра – 10 мм рт. ст.

2. Ціна поділки шкали металевого манометра – 0,05 ат.

3. Верхня межа вимірювання тиску металевим манометром – 2,5 ат.

4. Різниця рівнів ртуті в рідинному манометрі – h = 340 мм.

5. Різниця рівнів ртуті в рідинному манометрі в Па.-  45220 Па.

6. Абсолютний тиск газу в об’ємі V₁ = 20 л.

      р₁ = р_атм + h,    р₁ = 100 000 Па + 133 Па · 340 = 145 220 Па,    р₁ = 1,45 ат.

7. Абсолютний тиск газу в об’ємі V₂ = 26 л.

      р₂ = 1 ат + 0,35 ат = 1,35 ат.

8. Абсолютний тиск газу в обох посудинах після відкриття крану:

      р ( V_{1  +} V₂) = р₁V₁ + р₂V₂

     р = 1,45 ат ·20 л + 1,35 ат · 25 л /20 л + 25л  = 1,4 ат

9. Покази металевого манометра після відкриття крану: 1,4 ат – 1 ат = 0,4ат.   10. Різниця рівнів ртуті на ртутному манометрі після відкриття крану:

     0,4 · 100 000 / 133 Па = 300 мм.

11. Абсолютний тиск газу після охолодження до –73 ^оС = 200 ^оК

              але     V₁=V     тоді  

12. Мас  газу      

 

 

3 Серія – Графіки ізотерми і адіабати газу

На карточках 3 серії подані зображення графічної залежності тиску однієї й тієї ж маси газу від його об’єму: а) при ізотермічному, б) при адіабатичному процесах.

Універсальну газову сталу для спрощення розрахунків брати рівною -

8000 дж / (град · моль) чи 0,08 л · ат / (град · моль).

Молекулярну масу газу брати з таблиці.

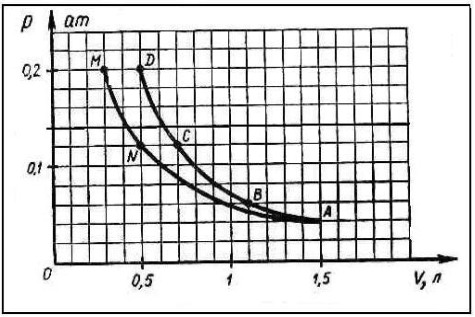
Наприклад для карточки № 8 відповіді учня будуть виглядати так:

Рис. 3.3. Приклад карточки 3 серії (№ 8).

1. Сторона клітинки відповідає об’єму -  0,01 л.
2. Сторона клітинки відповідає тиску -   0,02 ат.
3. Ізотермою на графіку являється крива ANM, так як добуток газу на  об’єм в усіх станах, відмічених точками на цій кривій, залишається незмінним і рівним 0,06 л · ат:  рV = 0,06 л · ат.
4. Різниця об’ємів між станами А і М -  1200 см³.

5.Різниця добутків тиску газу на його об’єм між станами Д і М

    (0,2 л ·0,5 ат) – (0,2 л ·0,3 ат) = 0,04 л · ат = 40 дж.

6. Різниця тисків між станами М і А -    0,16 ат.

7. Різниця тисків між станами м і А -    120 мм рт. ст.

8. Температура газу в стані Д , якщо в стані А температура газу Т_А=300 ^оК.                                      

9.Різниця температур між станами М і D газу рівна                                        Т_D – Т_М = 500 ^оК – 300 ^оК = 200 ^оК.

10.Різниця  температур між станами М і  D газу рівна  -73 ^оС.

11. Маса газу вирахувана за рівнянням Мєнділєєва – Клапейрона:

12. Густина газу в стані С :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 1.Розв’язування задач є однією з найважливіших ділянок роботи в системі навчання фізики в школі. Задачі є інструментом формування фізичних понять, розвитку мислення учнів, їхньої самостійності, засобом контролю якості і глибини засвоєння навчальної інформації тощо.

Фізична задача – це ситуація, яка вимагає від учня мислительних і практичних дій, що грунтуються на знанні ним понять і законів фізики, і направлена на закріплення, поглиблення і розвиток цих знань, на формування  умінь застосовувати їх на практиці, а також на розвиток наукового мислення.

         2. Існують різноманітні типи задач, а отже, і різні їх класифікації: за                                змістом, за способом подання умови, за дидактичною метою, за основним методом розв’язування, за глибиною дослідження питання, за ступенем трудності.

         3.У процесі розв’язування задач дотримуються певної послідовності етапів розв’язування.

         4.У процесі навчання учнів розв’язувати задачі, вчителі зазнають труднощів: вони добре їх розв’язують, але недостатньо знають методику навчання учнів розв’язувати задачі.

       5.Вчитель повинен використовувати ряд засобів і прийомів для активізації пізнавальної діяльності учнів на всіх етапах роботи над задачами: висунення гіпотез і пропозицій; вказівки на практичне значення задач; використання фрагментів телевізійних передач, кінофрагментів, діапозитивів, транспарантів до графопроектора, фотографій, малюнків, графіків, схем, креслень, приладів і установок тощо; аналіз спостережень, експериментальних задач; використання науково-популярної, довідкової та художньої літератури.

6.Під наочними задачами розуміють такі задачі, для розв’язання яких всі дані учні отримують самостійно, сприймаючи зором ситуацію, яка відображена на малюнку чи фотографії.

  Перевагою задач такого типу порівняно з експериментальними задачами є також те, що їх можна розв’язувати фронтально, оскільки фотографії можна  розмножити в будь-якій кількості.

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

1. Босенко Ф.З. Наочність при розв^,язуванні задач з фізики:Методичний посібник для вчителів. – К.: Рад. Школа, 1971 – 120с.
2. Виговська О.І. Удосконалення підготовки вчителів до розв^,язування фізичних задач. // Розв^,язування задач з фізики: Збірник статей /За ред. Є.В. Коршака – К.: Рад. Школа, 1989. – С. 54-57.
3. Калапуша Л., Кобель Г., Швай О.Моделювання у процесі розв^,язування задач з фізики.  Л.: Редакційно - видавничий  відділ  ВДУ ім. Лесі  Українки,  1997. – С.22 –25.
4. Коршак Є.В., Гончаренко С.У., Коршак Н. М. Методика розв^,язування задач з фізики. К.: Вища школа, 1976. – 239 с.
5. Сиротюк В. Засоби наочності у розв^,язуванні фізичних задач. // Фізика та астрономія в школі. – 1997. -№3. – С. 50-54.
6. Скрелин Л. И. Дидактический материал по физике, 9 класс: Пособие для учителей. – М.: Просвещение, 1976 – 143.
7. Ушаков М.А. Наглядные задачи по физике. //Фізика в школі. – 1982 - №2 – С. 31 – 33.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Д  О   Д   А   Т   К  И