Науково-дослідницька робота «Фрактальність берегової лінії Азовського моря».

Міністерство освіти і науки України
Департамент освіти і науки Донецької облдержадміністрації
Обласна науково-практична конференція учнівської молоді
«Біологічні дослідження та винахідництво»

Секція «Винахідницькі та раціоналізаторські проекти еколого-

натуралістичного напряму».

ФРАКТАЛЬНІСТЬ БЕРЕГОВОЇ ЛІНІЇ

АЗОВСЬКОГО МОРЯ

Роботу виконала:

Журба Кіра,  учениця 6 класу

Новоекономічної   ЗОШ  І-ІІІ ступенів

Покровської райради  Донецької області

Педагогічний керівник:

                                              Калашник Наталія Іванівна,

                                 вчитель математики

                                                            Новоекономічної ЗОШ І-ІІІ ступенів

                                                                       Покровської райради Донецької області

                                                       Слов’янськ    -  2019

Тези
    науково-дослідницької роботи на тему:

 «Фрактальність берегової лінії Азовського моря».

Автор:

Журба Кіра, учениця 6 класу

Новоекономічної ЗОШ І-ІІІ ступенів Покровської райради Донецької області

Педагогічний керівник:

Калашник Наталія Іванівна,  вчитель математики

 Новоекономічної ЗОШ І-ІІІ ступенів Покровської райради Донецької області

Метою роботи є аналіз теоретичних питань з даної теми, з’ясовування в  яких галузях застосовуються фрактали; проведення дослідів з вимірювання та фрактального дослідження  довжини берегової лінії Азовського моря на території України та виготовлення рукотворних фракталів.

Актуальність дослідження: оскільки фрактальна наука ще досить молода та не вивчається в шкільній програмі, то вона відома невеликому кругу людей. Але через здатність описувати предмети та явища з точністю до найдрібніших деталей, вона є перспективним напрямком науки,  і  тому тема є актуальною.

Новизна роботи полягає  у вивченні теоретичних питань, аналізі  застосування  фракталів у різних галузях; проведенні дослідів з вимірювання та фрактального дослідження  довжини берегової лінії Азовського моря на території України та виготовленні рукотворних фракталів.

Об’єктом дослідження є фрактали.

Предметом дослідження є довжина берегової лінії Азовського моря;  конкретні приклади використання фракталів у різних галузях; рукотворні фрактали.

Завдання науково-дослідницької роботи:

• визначити  поняття  фрактала; історію виникнення фракталів, їх вивчення;
• виявити сфери  практичного використання фракталів;
• дослідити довжину берегової лінії Азовського моря України, застосовуючи фрактальна техніку;
• виготовити рукотворні фрактали.

Наукова гіпотеза роботи: дослідження фракталів відкриває широкі можливості вивчення оточуючого світу. Вправи з виготовлення фракталів дозволяють  впоратись із тривогою, складають умови щоб заглибитись у себе,  поглиблюють  знання з математики,  інформатики та відновлюють  душевну рівновагу.

Проведене дослідження дозволило зробити такі висновки: у ході дослідження гіпотеза підтвердилася. Отже, концепція фракталів стає не тільки частиною "чистої науки", але й елементом загальнолюдської культури. Фрактальна наука ще дуже молода, і їй пророкують велике майбутнє. Краса фракталів далеко не вичерпана і ще подарує людству чимало шедеврів - тих, які радують зір, і тих які дають насолоду розуму

Зміст.

ВСТУП                                                                                                                                       4-5 стор.

Розділ 1.   Історія дослідження берегових ліній                                            6-8 стор.         

Розділ 2.  Дослідження  берегової лінії Азовського моря на Україні     9-10 стор.

Розділ 3.Рукотворні фрактали                                                                 11 стор.

Висновки                                                                                                     12 стор.

Використані ресурси                                                                                  13 стор.

Додатки                                                                                                             14-16 стор.

ВСТУП

БЕЗКОНЕЧНИК

Кури в полі сіють просо,

як заведено давно.

А півні те просо косять,

зрешетують на пшоно.

Із пшона наварять каші

жовторотій дітлашні...

Виростуть курчата наші,

стануть кури та півні —

і почнеться все спочатку,

все спочатку по порядку:

кури сіятимуть просо,

 як заведено давно,

а півні те просо скосять,

зрешетують на пшоно.

Із пшона наварять каші

жовторотій дітлашні,

виростуть курчата наші,

стануть кури та півні —

і почнеться все спочатку,

все спочатку по порядку...

Іван Світличний

Дуже часто, самі не підозрюючи того, ми маємо справу з фракталами. Ми звертаємось до геометрії, коли працюємо з формою та розмірами, предметами, їх розміщенням в просторі. А що таке геометрія? Наука про форми і розміри предметів, а також взаємне розміщення фігур називається геометрією. Застосування цієї науки в житті зустрічається дуже часто: в будівництві, ландшафтному дизайні, архітектурі та інтер'єрі. Фрактали застосовують  для прикрас у кімнатах – декорують стіни та натяжні стелі;  посуд, одяг, транспорт – тюнер автомобілів  та мотоциклів.  За допомогою фрактальних технологій вимірюють довжини берегових ліній.  Все це спонукало нас до вибору теми науково-дослідницької роботи «Фрактальність берегової лінії Азовського моря».

Метою роботи є аналіз теоретичних питань з даної теми, з’ясовування в  яких галузях застосовуються фрактали; проведення дослідів з вимірювання та фрактального дослідження  довжини берегової лінії Азовського моря на території України та виготовлення рукотворних фракталів.

Актуальність дослідження: оскільки фрактальна наука ще досить молода та не вивчається в шкільній програмі, то вона відома невеликому кругу людей. Але через здатність описувати предмети та явища з точністю до найдрібніших деталей, вона є перспективним напрямком науки,  і  тому тема є актуальною.

Новизна роботи полягає  у вивченні теоретичних питань, аналізі  застосування  фракталів у різних галузях; проведенні дослідів з вимірювання та фрактального дослідження  довжини берегової лінії Азовського моря на території України та виготовленні рукотворних фракталів.

Об’єктом дослідження є фрактали.

Предметом дослідження є довжина берегової лінії Азовського моря;  конкретні приклади використання фракталів у різних галузях; рукотворні фрактали.

Завдання науково-дослідницької роботи:

• визначити  поняття  фрактала; історію виникнення фракталів, їх вивчення;
• виявити сфери  практичного використання фракталів;
• дослідити довжину берегової лінії Азовського моря України, застосовуючи фрактальна техніку;
• виготовити рукотворні фрактали.

Наукова гіпотеза роботи: дослідження фракталів відкриває широкі можливості вивчення оточуючого світу, а тому, користуючись фрактальним методом,  заміри Азовського узбережжя  максимально приблизяться до дійсності.  Вправи з виготовлення фракталів дозволяють  впоратись із тривогою, складають умови щоб заглибитись у себе,  поглиблюють  знання з математики,  інформатики та відновлюють  душевну рівновагу.

Розділ 1.   Історія дослідження берегових ліній

Незадовго до 1951 року  Льюїс  Фрай  Річардсон  в  ході  дослідження передбачуваного впливу довжини державних кордонів на вірогідність початку військових конфліктів помітив наступне: Португалія заявила, що її сухопутний кордон з Іспанією дорівнює 987 км, а Іспанія визначила його рівним 1 214 км. Цей факт послужив відправною точкою для вивчення проблеми берегової лінії.

Основним методом оцінки довжини кордону або берегової лінії було накладення N рівних відрізків завдовжки / на карту або аерофотознімок за допомогою циркуля. Кожен кінець відрізку повинен належати вимірюваній лінії. Досліджуючи розбіжності в оцінці меж, Річардсон виявив те, що зараз називається ефектом Річардсона: масштаб вимірів обернено пропорційний до загальної довжини усіх відрізків. Тобто чим коротше використовувана лінійка, тим довше вимірювана межа. Таким чином, іспанські і португальські географи просто керувалися вимірами різних масштабів.

Найбільш вражаючим для Річардсона виявилося те, що коли величина l прагне до нуля, довжина узбережжя прагне до нескінченності. Спочатку Річардсон вважав, спираючись на геометрію Евкліда, що ця довжина досягне фіксованої величини, як це відбувається у випадку з правильними геометричними фігурами. Наприклад, периметр правильного багатокутника, вписаного в коло, наближається до довжини самого кола зі збільшенням числа сторін (і зменшенням довжини кожної сторони). У теорії геометричних вимірів така гладка крива, як коло, яке може бути приблизно представлене у вигляді невеликих відрізків із заданою межею, називається спрямлюваною кривою.

Понад десять років після завершення Річардсоном своєї роботи Мандельброт розробив нову гілку математики — фрактальну геометрію — для опису таких існуючих в природі комплексів, що не випрямляються, як нескінченна берегова лінія. Його власне визначення фрактала як основи його дослідження таке:

Ключовою властивістю фракталів є самоподібність, що полягає в прояві однієї і тієї ж загальної фігури на будь-якому масштабі.

Берегова лінія сприймається як чергування заток і мисів. Гіпотетично, якщо ця берегова лінія має властивість самоподібності, то незалежно від того, наскільки сильно масштабується та або інша частина, все одно проявляється аналогічна картина менших заток і мисів, накладена на більші затоки і миси, аж до піщинок. На таких масштабах берегова лінія виявляється ниткою, що миттєво змінюється, потенційно нескінченно, із стохастичним розташуванням заток і мисів. У таких умовах (на відміну від гладких кривих) Мандельброт стверджує: «Довжина берегової лінії виявляється недосяжним уявленням, що ковзає між пальцями тих, хто намагається його зрозуміти».

Довжина берегової лінії залежить від способу її вимірювання. Оскільки для ділянки суші можна виділити вигини будь-якого розміру, від сотень кілометрів до доль міліметра і менше, не можна очевидним чином підібрати розмір найменшого елементу, який має бути узятий для вимірювання. Отже, не можна однозначно визначити і периметр цієї ділянки. Існують різні математичні наближення для розвязання цієї задачі.

У 1977 р. американський математик Бенуа Мандельброт поставив перед собою наступне питання: чому рівна довжина берегової лінії Великобританії? Виявилось, що коректно відповісти на це "дитяче питання" не вдається. У 1988 р. норвезький учений Енс Федер вирішив з'ясувати, чому рівна довжина берегової лінії Норвегії. Звернете увагу на те, що побережжя Норвегії сильно порізане фіордами. Інші учені ставили собі аналогічні питання про довжини берегових ліній побережжя Австралії, Південної Африки, Німеччини, Португалії і інших країн.

Ми можемо зміряти довжину берегової лінії тільки приблизно. У міру того як ми зменшуємо масштаб, нам доводиться вимірювати все більше маленьких мисів і бухт - довжина берегової лінії збільшується, і об'єктивної межі зменшенню масштабу (і, тим самим, збільшенню довжини берегової лінії) просто не існує; ми вимушені визнати, що ця лінія має нескінченну довжину. Ми знаємо, що розмірність прямої лінії рівна одному, розмірність квадрата - двом, а розмірність куба - трьом. Мандельброт запропонував використовувати для вимірювання "жахливих" кривих дроби розмірності. Коефіцієнт D називається фрактальною розмірністю. Слово фрактал походить від латинського слова fractal - дріб, нецілий. Множина називається фрактальною, якщо воно має нецілу розмірність. Для Норвегії D=1,52, а для Великобританії D=1,3. Таким чином, берегова лінія Норвегії і Великобританії - фрактал з фрактальною розмірністю D. Розрахунки були також проведені і для кола, і фрактальна розмірність кола D=1, що і слід було чекати. Таким чином, фрактальна розмірність - узагальнення звичайної розмірності.

    Норвезький учений Е. Федер, запропонували інший спосіб вимірювання довжини берегової лінії. Карту покрили квадратною сіткою, осередки якої мають розміри е ?  Видно, що число N(e) таких осередків, які покривають берегову лінію на карті, приблизно рівне числу кроків, за яке можна обійти по карті берегову лінію циркулем з розчином e. Якщо е зменшувати, то число N(e) зростатиме. При зменшенні кроку зміряна довжина зростає. Виявилось, що взаємозв'язок зміряної довжини L(e) і кроку e може бути описана наближеним співвідношенням.

Розділ 2.  Дослідження  берегової лінії Азовського моря на Україні

 Один з відомих прикладів застосування фрактала — нескінченна довжина берегової лінії будь - якого острова чи частини материка.

Надихнувшись вимірюванням берегових  ліній вченими, ми  провели дослідження довжини української берегової лінії Азовського моря, використовуючи фізичну карту України з М 1: 1000000.

 Перший дослід. Виміряли довжину української берегової лінії Азовського моря лінійкою на фізичній карті України та  використавши масштаб, знайшли її довжину 12,8 см на карті, натуральна довжина -   - 1280 км.

Другий дослід. Лінійку замінили ниткою. Довжина збільшилася, стала – 13,9 см на карті, натуральна довжина -  1390 км.

 Третій дослід. Користувалися при вимірюванні мокрою ниткою, яка більш  слухняно  закладалася на карті в дрібні западини і бухти.  Довжина експертної території знову збільшилася і стала 14,8 см на карті, натуральна довжина - 1480   км.

Четвертий дослід. У якому довжину берегової лінії вимірювали циркулем, змінюючи довжину відстані між кінцями прилада (радіус). Результати занесені до таблиці 1.

                                                                                                               Табл.1

П’ятий дослід. Знаходження даних про протяжність Азовського моря на території України  в Інтернеті.  На сайті у Заставного Ф.Д. «Фізична географія України» [12] повідомляється, що  Азовське море омиває південно-східні береги України. Це внутрішнє море басейну Атлантичного океану. Його площа становить 39 тис. км кв, пересічна глибина 7-10 м, максимальна — 15 м. Його протяжність 1480 км.

На сайті «Народна освіта»[13] - «Загальна протяжність берегової лінії — 2686 км (у межах України — 1472 км, 56%)».

Матеріал з Вікіпедії [14] — вільної енциклопедії: «Найбільша його довжина — 343 км, найбільша ширина — 231 км; довжина берегової лінії — 1472 км; площа поверхні — 37605 км² (у цю площу не входять острови і коси, що займають 107, 9 кв. км).»

Фрактальний світ добре відображає реальний, оскільки властивості фракталів демонструють багато природних об’єктів. Тому часто говорять, що книга природи написана мовою фракталів. Така дивна схожість реального і фрактального світів обумовлена, перш за все, тим, що властивості фізичного світу змінюються повільно із зміною масштабів. У піску на березі багато властивостей спільних із властивостями гальки, гори мають багато спільного із каменями, що їх складають, маленький струмочок  багато в чому схожий на велику річку. Саме така незмінність відносно масштабу – характерна риса фракталів. Проведене дослідження берегової лінії Азовського моря на Україні наочно демонструє  якість вимірювання при застосуванні фрактальної технології.

 Розділ 3.Рукотворні фрактали

До рукотворних відносяться ті фрактали, які були придумані вченими, виготовлені людиною, які  при будь-якому масштабі володіють фрактальними властивостями.

Вивчивши  фрактальна правила, ми виготовили декілька геометричних та стохастичних експонатів, що розміщені в додатку.

Для їх виготовлення ми користувалися різними техніками:

• орнамент - фрактальний малюнок, малюється з заплющеними очима. Використовується в психології для діагностики його автора (додаток. Рис.1);
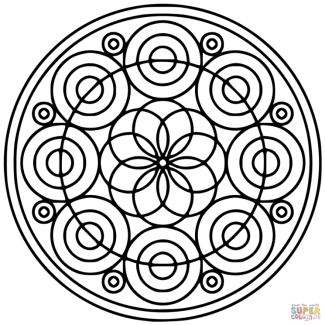
• плетіння мандали - сакрального символу  індуїзму та буддизму. Це складна  фрактально- геометрична фігура – модель Всесвіту,  вона має глибокий зміст (додаток. Рис.2);
• виготовлення об’ємних фігур за допомогою холодних 3D ручок - трикутна піраміда, приклад  фрактала, бо кожний з трикутників  складається з менших трикутників (додаток. Рис.3);                                                                     Рис.6
• орігамі -  рукотворний  фрактал відноситься до  геометричних фракталів. Це вирізані куби , які за будовою нагадують піраміду (додаток. Рис.4);
• геометричне креслення  - круговий фрактал , це декілька кругів, вписаних одне в одне так, щоб не перетинатися (додаток. Рис.5).

Зупинимося на поясненні поняття «мандала». Мандала — це геометричний символ складної структури, який інтерпретується як модель Всесвіту, «карта космосу», вираження усього. Типова форма мандали — зовнішнє коло з вписаним у нього квадратом, куди поміщено внутрішнє коло (часто сегментоване), або ж представлене у формі лотосу. (Рис.6)                                                                                                          

На наш погляд фрактали вийшли цікавими, яркими та наочними. Вони знадобляться учням та вчителям для ознайомлення з теорією фракталів.

Висновки

     Присутність фрактала з першого погляду можна і не помітити, якщо не заглиблюватись у досконале вивчення математики. Ця наука, дійсно, не має меж і постійно спонукає до різноманітних досліджень.

Фрактал — це математична величина, що зустрічається досить часто.  Абсолютно точна, алгебраїчна величина, яка творить собою неймовірні фігури, візерунки та складає цікаві орнаменти, що ми зустрічаємо кожного дня. Це і листя папороті, і маленькі сніжинки та ще багато іншого.

З кожним роком поняття фрактала стає відоме все більш широкому колу людей. І зараз цей термін важко залишити без належної уваги. У природі є багато чого, що має прямий зв’язок до цього терміну.

Наостанок зазначимо, що у ході дослідження гіпотеза підтвердилася. Дослідження фракталів відкриває широкі можливості вивчення оточуючого світу, а тому, користуючись фрактальним методом,  заміри Азовського узбережжя  максимально приблизилися до дійсності і навіть стали більшими..

 Виготовлені рукотворні фрактали: кругова, мандала, об`ємна – трикутник Серпінського, при виготовленні яких підтвердилась друга частина  гіпотези, що подібні вправи дозволяють  впоратись із тривогою, заглибитись у себе;  поглиблюють  знання з математики, мистецтва та відновлюють  душевну рівновагу.

Отже, концепція фракталів стає не тільки частиною "чистої науки", але й елементом загальнолюдської культури.

Фрактальна наука ще дуже молода, і їй пророкують велике майбутнє. Краса фракталів далеко не вичерпана і ще подарує людству чимало шедеврів - тих, які радують зір, і тих які дають насолоду розуму

Використані ресурси.

1. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.
2. . Федер Е. Фракталы. — М: «Мир», 1991.
3.  Фоменко А. Т. Наглядная геометрия и топология. — М.: изд-во МГУ, 1993.
4. Мандельброт Б. Фрактальна геометрія природи / Бенуа Мандельброт. – Москва : Інститут комп'ютерних досліджень. –2002. – 656 с.
5. Корнійчук О. Мотивація в системі навчання математичних дисциплін / Олена Корнійчук // Витоки педагогічної майстерності. Сер. Педагогічні науки. – Полтава : ПНПУ ім. В.Г. Короленка, 2012.– Вип. 10. – С. 144-148.
6. https://uk.wikipedia.org/wiki/%D0%9C%D0%B0%D0%BD%D0%B4%D0%B0%D0%BB%D0%B0 «Мандала»
7.  http://en.wikipedia.org/wiki/Fractal
8.  http://en.wikipedia.org/wiki/Mandelbrot_set
9.  http://en.wikipedia.org/wiki/Julia_set
10.  http://en.wikipedia.org/wiki/Newton_fractal
11.  http://en.wikipedia.org/wiki/Fractal_art
12.  http://commons.wikimedia.org/wiki/Fractal  Заставний Ф.Д.Фізична географія України.
13. http://narodna-osvita.com.ua/3400--39-azovske-more.html Народна освіта §«Азовське море».
14. https://uk.wikipedia.org/wiki/%D0%90%D0%B7%D0%BE%D0%B2%D1%81%D1%8C%D0%BA%D0%B5_%D0%BC%D0%BE%D1%80%D0%B5 Азовське море. Матеріал з Вікіпедії — вільної енциклопедії.

Додатки.

Рис.1

Рис.2

Рис.3

                     Рис.4

                                                                                                            Рис.5.