Науково-дослідницька робота «Розв’язування систем лінійних алгебраїчних рівнянь»

Відділ освіти виконкому Тернівської районної в місті ради

Криворізька загальноосвітня школа

I-III ступенів №61

Дніпропетровської області

 

 

 

 

 

 

 

 

Науково – дослідницька робота

 

«Розв’язування систем лінійних алгебраїчних рівнянь»

 

 

 

     

 

 

 

 

Виконала роботу учениця 9 класу

КЗШ № 61

Науковий керівник:

вчитель математики

Шаміна Лариса Станіславівна

Вища категорія

 

 

 

 

 

 

 

м. Кривий Ріг

Зміст

Вступ …………………………………………………………………….3

Розділ I Система лінійних рівнянь…………………………………...4-6

Розділ II  Розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса…………………………………………………………………..7-10

Розділ III Розв’язування систем лінійних алгебраїчних рівнянь матричним методом…………………………………………………..11-13

Розділ IV Розв’язування систем лінійних алгебраїчних рівнянь за правилом Крамера……………………………………………………14-15                                                                                                          

Розділ V Застосування методів на прикладах……………………....16-23

Розділ VI Приклади для самостійного розв’язування……………....24

Висновок……………………………………………………………….25

Список використаної літератури…………………………………...26

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

Об’єкт дослідження:     система трьох лінійних рівнянь з                                                                                 трьома змінними 

Предмет  дослідження:     розв’язування систем лінійних                                                                               рівнянь з трьома невідомими.

Мета дослідження:        поглибити знання і вміння                                                                                        розв’язування систем лінійних                                                                                                              рівнянь з трьома невідомими.

Методи дослідження:    аналітичний,

      пошуковий,

      синтетичний.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ I Система лінійних рівнянь

Лінійним рівнянням називають рівняння виду

a₁x₁+a₂x₂+a₃x₃+...+a_nx_n=b,

де (а₁, а₂, ... а_n) - довільні дійсні числа, які називаються коефіцієнтами при невідомих (х₁, х₂, ... х_n);

b- вільний член, який може набувати довільного дійсного значення.

 Якщо розглядати декілька лінійних рівнянь разом і ставити завдання знайти значення невідомих, які задовольнятимуть одночасно кожне з цих рівнянь, то

матимемо систему лінійних рівнянь (СЛР):

 

      a₁₁x₁+ a₁₂x₂ +a₁₃x₃+…+ a_1nx_n= b₁;

a₂₁x₁+ a₂₂x₂+ a₂₃x₃+…+ a_2nx_n= b₂;                    (1)

      ………………………………

      a_m1x₁+ a_m2x₂+ a_m3x₃+…+ a_mnx_n= b_n;

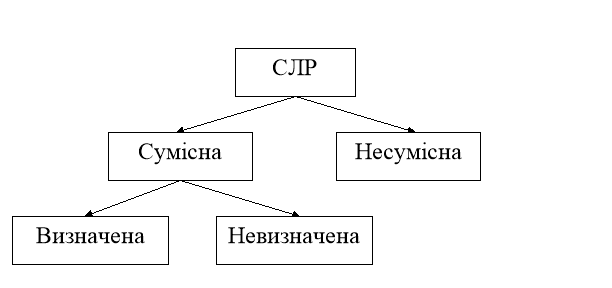
СЛР (1) в залежності від її елементів може мати:

1. один розв’язок;
2. безліч розв’язків;
3. зовсім не мати розв’язку.

У перших двох випадках СЛР називається сумісною, в третьому випадку - несумісною.

Сумісна СЛР називається визначеною, якщо вона має єдиний розв’язок, і називається невизначеною, якщо вона має безліч розв’язків.

Дві системи лінійних рівнянь з однаковим числом невідомих називаються рівносильними (еквівалентними), якщо вони мають однакові розв’язки або обидві несумісні.

Від заданої СЛР до рівносильної її системи можна прийти за допомогою елементарних перетворень, до яких відносяться:

1. перестановка (транспозиція) двох довільних рівнянь системи місцями;
2. множення обох частин довільного рівняння на відмінне від нуля число (або ділення);
3. додавання до довільного рівняння системи іншого рівняння, помноженого, на відмінне від нуля число.

 

Для довільної системи лінійних рівнянь виконується: система або несумісна, або система яка має єдиний розв’язок, або система яка має безліч розв’язків.

 

 

 

 

Розглянемо СЛР (1) для трьох невідомих:

     a₁x+ b₁y+ c₁z= d₁;

     a₂x+ b₂y+ c₂z= d₂;                                             (2)

     a₃x+ b₃y+ c₃z= d₃;

     де a₁, b₁, ... , b₃, c₃- задані коефіцієнти;

     d₁, d₂, d₃- задані вільні члени;

      x, y, z- невідомі.

Множина чисел x₀, y₀, z₀ називається розв’язком СЛР (2), якщо при   

       підстановці x=x₀, y=y₀, z=z₀ в СЛР (2) отримаємо числові тотожності.

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ II Розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса.

 

Одним з широко відомих методів розв’язування СЛР є метод Гауса, який полягає в послідовному виключенні невідомих шляхом елементарних перетворень:

1. переміна місцями рівнянь системи;
2. почленне множення обох частин одного з рівнянь на відмінне від нуля число;
3. додавання до обох частин одного з рівнянь відповідних частин іншого рівняння.

Почнемо розв’язання СЛР (2) з виключення невідомого х в другому, а тоді і в третьому рівняннях. Для цього помножимо обидві частини першого рівняння системи (2) на (-а₂), а обидві частини другого рівняння на а₁, після чого додамо відповідні частини цих рівнянь. Результат цих елементарних перетворень матиме вигляд:

-а₁а₂х- b₁a₂y- c₁a₂z= -d₁a₂

+

 A₂a₁x+ b₂a₁y+ c₂a₁z= d₂a₁

___________________________

0·x+ (a₁b₂- a₂b₁)y+ (a₁c₂-a₂c₁)z= a₁d₂+ a₂d₁,

або, позначивши

 

b´₂= a₁b₂- a₂b₁,  c´₂= a₁c₂- a₂c₁,  d΄₂= a₁d₂- a₂d₁,

запишемо нове рівняння:

0·x+ b΄₂y+ c΄₂z= d΄₂

Отже, в другому рівнянні ми виключили невідоме х, тобто коефіцієнт при х став рівним нулю.

Аналогічно одержуємо b΄₃= a₁b₃- a₃b₁,

                                         c΄₃= a₁c₃- a₃c₁,

                                         d΄₃= a₁d₃- a₃d₁.

Після цього третє рівняння матиме вигляд 0·x+ b΄₃y+ c΄₃z= d΄₃.

Запишемо нову систему, еквівалентну системі (2):

 a₁x+ b₁y+ c₁z= d₁,

         b΄₂y+ c΄₂z= d΄₂,                  (3)

         b΄₃y+ c΄₃z= d΄₃.

Вважаючи, що b΄₂≠0, виберемо його провідним елементом і виключимо y в третьому рівнянні за відомим правилом.

Складаємо нову систему, яка еквівалентна системі (3), а значить, і СЛР (2)

 a₁x+ b₁y+ c₁z= d₁,

         b΄₂y+ c΄₂z= d΄₂,                  (4)

         c΄΄₃z= d΄΄₃.

Таким чином, систему (2) ми звели до еквівалентної, що має трикутну форму, системи (4), яка вже розв’язується легко. Знаходження x, y, z  із СЛР (4) називається зворотним ходом.

На практиці розв’язання систем лінійних рівнянь зручно вести за допомогою обчислювальної таблиці:

№	Коефіцієнти при			Вільні члени	Суми	Контроль
	х	у	z
	1	2	3	4	5	6
1	а1	b1	c1	d1	S1
2	а2	b2	c2	d2	S2
3	а3	b3	c3	d3	S3
4	0	b2'	с2'	d2'	S2'	2'
5	0	b3'	с3'	d3'	S3'	3'
6	0	0	с3''	d3''	S3''	3''

 

В таблиці    S₁ = a₁+b₁+c₁+d₁,

   S₂ = a₂+b₂+c₂+d₂,     - це суми елементів відповідних рівнянь.

           S₃ = +b₃+c₃+d₃,

В рядках 4 і 5 елементи перетворених за правилом прямокутника другого і третього рівнянь системи (2), а

  S₂' = b₂'+c₂'+d₂'_,

                  S₃' = b₃'+c₃'+d₃',

В шостому рядку елементи перетвореного третього рівняння системи

                 S₃'' = c₃''+d₃'',

У стовпчику «контроль» записані результати перетворень за правилом прямокутника значень сум S₂ і S₃,тобто

     ₂' = a₁S₂ - a₂S₁= a₁ (a₂+b₂+c₂+d₂) - a₂(a₁+b₁+c₁+d₁)= (a₁a₂ - a₂a₁) +

(a₁b₂- a₂b₁) + (a₁c₂- a₂c₁) + (a₁d₂- a₂d₁) = 0 + b₂'+c₂'+d₂'= S₂'

                ₃' = a₁S₃ - a₃S₁ = S₃'

Аналогічно             ₃'' = b₁S₃' - b₃S₂' = S₃''

 Те, що суми S і      у стовпчиках 5 і 6 збігаються свідчить про вірність поточних результатів обчислень.

 Після заповнення всіх рядків 1-6 таблиці на основі даних в рядках 1,4,6 записуємо трикутну систему, з якої тоді починається зворотній хід.

 Метод Гаусса досить зручний для розв’язування вручну систем лінійних рівнянь з невеликою кількістю невідомих. Він з успіхом може бути використаний також для розв’язування лінійних систем на ЕОМ.      

 

 

 

 

 

 

Розділ III Розв’язування систем лінійних алгебраїчних рівнянь матричним методом.

Розглянемо систему лінійних рівнянь:

 a₁₁x + а₁₂y + а₁₃z = b₁                                      

 a₂₁x + а₂₂y + а₂₃z = b₂

 a₃₁x + а₃₂y + а₃₃z = b₃

Запишемо такі матриці;

 

          a₁₁  а₁₂  а₁₃               

А =   a₂₁  а₂₂  а₂₃

        a₃₁  а₃₂  а₃₃

         х                        b₁

Х =   у               В =   b₂

         z                        b₃

де А складена з коефіцієнтів при невідомих – матриця системи, В – матриця вільних членів, Х матриця невідомих. Знайдемо добуток

 

           a₁₁  а₁₂  а₁₃       х      a₁₁х  а₁₂х  а₁₃х              

А =     a₂₁  а₂₂  а₂₃        у     a₂₁у  а₂₂у   а₂₃у       

          a₃₁  а₃₂ а₃₃       z      a₃₁z  а₃₂z  а₃₃z        

 

 Користуючись означенням рівності матриць, ми бачимо, що система ЛР є не що інше, як рівність відповідних елементів матриць стовпців АХ і В. Тому початкова система набуває форму матричного рівняння АХ = В

 Для розв’язання останнього помножимо зліва рівняння на обернену матрицю  А^-1 , вважаючи, що det А≠0, отримаємо

 А^-1 АХ= А^-1 В

Але А^-1 А = Е, а ЕХ=Х, тоді розв’язок матричного рівняння запишеться Х = А^-1 В

 Покажемо, що з формули можна отримати формули Крамера. Дійсно, підставляючи в розв’язок матричного рівняння вирази А^-1 і В, маємо

 

           х         1    А₁₁  А₂₁  А₃₁           b₁          1       А₁₁b₁  А₂₁b₁  А₃₁b₁

А =     у   =   ―   А₁₂  А₂₂   А₃₂          b₂     =   ―     А₁₂b₂  А₂₂b₂   А₃₂b₂    

          z                 А₁₃  А₂₃  А₃₃        b₃                 А₁₃b₃  А₂₃b₃  А₃₃b₃

  

 За теоремою про зміщення кожний елемент останньої матриці дорівнює значенням допоміжних визначників х, у, z, які були введені при розв’язуванні систем за формулами Крамера.

 Тому далі маємо:

           х         1      х

Х =     у   =   ―     у      x =       ;  y =        ; z =      

  z                  z                                               

 

 Звернемо увагу на те, що в формулі співмножник А^-1, залежить тільки від коефіцієнтів при невідомих, а В тільки від вільних членів. Тому, коли приходиться розв’язувати системи такого вигляду, з однаковими лівими частинами і різними вільними членами, то в таких випадках матричний розв’язок стає зручнішим: обернену матрицю А^-1знаходимо тільки один раз і перемножуємо на нову матрицю В.

Алгоритм розв’язання

1. Скласти матрицю А,В,Х.

2. Обчислити визначник матриці А

3. Скласти А^Т  - транспоновану матрицю для матриці А.(Для цього необхідно в матриці А записати рядки стовпцями)

4. Обчислюємо алгебраїчні доповнення А_ij елементів визначника матриці А^Т за формулою А_ij = (-1)^p · Mij

де Mij – мінор, р = i + j,  ij – індекси при коефіцієнтах

5. Скласти А^-1 – обернену матрицю, яка складається з алгебраїчних доповнень.

 

       х        1

6.    у   = ― ·А^-1 ·В

      z      

 

 

 

Розділ IV Розв’язування систем лінійних рівнянь за методом Крамера

Система трьох лінійних рівнянь з трьома невідомими має вигляд:

a₁x + b₁y + c₁z = d₁                                      

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃

 

де a_i , b_i , c_i ,d _i – довільні числа (i = 1,2,3), x, y, z – шукані невідомі.

Складемо із коефіцієнтів при невідомих таблицю:

 a₁  b₁  c₁

 a₂  b₂  c₂

 a₃  b₃  c₃

 

Вона називається матрицею третього порядку. Міркуючи, аналогічно, отримуємо визначник третього порядку .

 

              a₁  b₁  c₁

 =      a₂  b₂  c₂       = a₁b₂c₃ + a₃b₁c₂ + a₂b₃c₁ – a₃b₂c₁ – a₁b₃c₂ – a₂b₁c_3.

              a₃  b₃  c₃

 

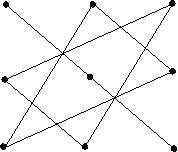
Такі визначники третього порядку зручно обчислювати дотримуючись схеми:

 

 

 

 

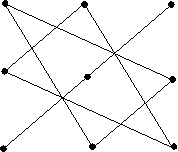
            Схема 1                                               Схема 2

Відрізками з’єднані три елементи, які перемножуються. Зі знаком «+» (схема 1) беруться добутки елементів головної діагоналі і вершин трикутників, в яких сторона паралельна головній діагоналі.

Зі знаком « – » (схема 2) беруться добутки елементів допоміжної діагоналі і вершин трикутників, в яких сторона паралельна допоміжній діагоналі.

Якщо тепер по черзі кожен стовпець замінити вільними членами, то дістанемо три нові визначники:

 

      d₁  b₁  c₁

_x  =     d₂  b₂  c₂       = d₁b₂c₃ + b₁c₂d₃ + d₂b₃c₁– d₃d₂c₁– b₃c₂d₁– d₂b₁c₃

      d₃  b₃  c₃

 

              a₁  d₁  c₁

_y  =     a₂  d₂  c₂      = a₁d₂c₃ +a₃d₁c₂+ a₂d₃c₁– a₃d₂c₁ –а₁d₃c₂ – a₂d₁c_3,

                     a₃  d₃  c₃ 

 

              a₁  b₁  d₁

_z =      a₂  b₂  d₂       = a₁d₂d₃ + a₃b₁d₂ + a₂b₃d₁ – a₃b₂d₁ – a₁b₃d₂ – a₂b₁d_3,

              a₃  b₃  d₃ 

 

Тоді, якщо  ≠ 0, дістанемо формули Крамера x =       ;  y =        ; z =       .

Якщо ж   = 0, то можливі такі випадки:

а) _х  ≠ 0, або _у  ≠ 0 або _z  ≠ 0. Тоді система розв’язків не має.

б) _х  = _у  = _z  = 0 – система має безліч розв’язків.

 

 

 

Розділ V Застосування методів на прикладах

1. Метод Гаусса.

№ 1. Розв’язати систему лінійних рівнянь.

x - 4y + 3z = 5;

2x - 7y + 2z = 3;

3x - 8y + 4z = 9;                                     

 

      

 1  -4   3   5

 2  -7   2   3

 3  -8   4   9

 

Помножимо перше рівняння на (-2) і додамо його до другого. Помножимо перше рівняння на (-3) і додамо його до третього. Отримаємо:  

 

 1  -4   3   5

 0   1   -4  -7

 0   4   -5  -6

 

Помножимо друге рівняння на (-4) і додамо його до третього.

Отримаємо:

 

 1  -4   3   5

 0   1   -4  -7

 0   0   11  22

 

 

 x - 4y + 3z = 5;              x = 3;

     7y - 4z = -7;               y = 1;

          11z = 22;               z = 2.

                   

Відповідь: ( 3; 1; 2).        

№2 Розв’язати систему лінійних рівнянь (за допомогою обчислювальної таблиці).

 

 

 

№ п/п	Коефіцієнти при			Вільні члени	Суми	Контроль
	x	y	z
	1	2	3	4	5	6
1	1	-4	3	5	5
2	2	-7	2	3	0
3	3	-8	4	9	8
4		1	-4	-7	-10	-10
5		4	-5	-6	-7	-7
6			11	22	33	33

 

 

 

Рядок 4

(4, 2):  – 2 · (– 4) – 7 = 1;

(4, 3):  – 2 · 3 + 2 = 4;

(4, 4):  5 · (– 2) + 3 = – 7;

(4, 5):  1 – 4 – 7 = – 10;

(4, 6):  5 · (– 2) + 0 = – 10.

 

Рядок 5

(5, 2):  – 4 · (– 3) – 8 = 4;

(5, 3):  – 3 · 3 + 4 = – 5;

(5, 4):  5 · (– 3) + 9 = – 6;

(5, 5):  4 – 5 – 6 = – 7;

(5, 6):  5 · (– 3) + 8 = – 7.

 

Рядок 6

(6, 3):  – 4 · (– 4) – 5 = 11;

(6, 4):  – 7 · (– 4) – 6 = 22;

(6, 5):  11 + 22 = 33;

(6, 6):  – 4 · (– 10) – 7 = 33.

 

За даними рядків 1, 4, 6 записуємо трикутну систему

    x – 4y + 3z = 5;

            y – 4z = – 7;

                11z = 22;

 

 

Зворотний хід.

z = 22  11 = 2;

y = – 7 + 4 · 2 = 1;

x = 4 · 1 – 3 · 2 + 5 = 3.

Відповідь: ( 3; 1; 2 ).

 

 

 

 

 

 

2. Матричний метод

 

x - 4y + 3z = 5;

2x - 7y + 2z = 3;

3x - 8y + 4z = 9;                                     

 

       1  -4   3  

А =   2  -7   2  

       3  -8   4  

 

          х                          8

Х =    у               В =     6

          z                          2

 

 

       1  -4   3  

|А| =   2  -7   2   = 11;

       3  -8   4  

 

 

       1   2   3  

А^Т =  -4  -7 -8  ;

       3   2   4  

 

        

А₁₁ =  -7 -8    = -12;

         2   4  

 

        

А₁₂ = -  -4 -8    = -8;

           3   4  

 

       

А₁₃ =   -4 -7    = 13;

         3   2  

 

       

А₂₁ = -   2  3    = -2;

           2  4  

 

 

А₂₂ =   1   3    = -5;

         3   4  

 

 

А₂₃ = -   1   2    = 4;

           3   2  

 

 

А₃₁ =   2   3    = 5;

        -7  -8  

 

 

А₃₂ = -   1   3    = -4;

           -4  -8  

 

 

А₃₃ =   1   2    = 1;

        -4  -7

 

 

       -12  -8   13  

А^-1 =  -2   -5    4    

        5   -4    1  

 

 

 

         х                    -12  -8   13     5                  -60  -24  +117                 33       3

         у    =  1/11    -2   -5    4    ·   3 = 1/11   -10  -15  +36     = 1/11   11  =   1

         z                     5   -4    1        9                   25  -12  +9                     22       2   

       

х = 3

у = 1

z = 2         

       

 

Відповідь: ( 3; 1; 2).         

 

 

 

 

 

 

 

 

 

3. Метод Крамера

 

 

№ 1. Розв’язати систему лінійних рівнянь.

x - 4y + 3z = 5;

2x - 7y + 2z = 3;

3x - 8y + 4z = 9

 

           1   -4    3                                

 =    2   -7    2   = -28 -48 -24 + 63 +32 +16 =11;

           3   -8    4

     

 

             5   -4    3                                

  _x=   3   -7    2   = -140 – 72 – 72 + 189 +48 + 80= 33;

             9   -8    4

     

 

             1    5    3                                

  _y =  2    3    2   = 12 + 30 + 54 – 27 – 40 – 18 = 11;

             3    9    4

     

 

             1    -4    5                                

  _z =  2    -7    3    = - 63 – 36 – 80 + 105 + 24 + 72 =22;

             3    -8    9

     

  

   x =       ;  y =        ; z =          

            

   x = 3; у =1; z = 2                  

  Відповідь: ( 3; 1; 2).         

 

           

 

 

 

 

 

 

№2. Розв’язати систему лінійних рівнянь.

    

      9x + 3y + 6z = 18;

     6x - 3y - 3z = 6;

     12x - 6y - 6z = 18;                                     

      

            9    3    6                                

 =    6   -3   -3   = 0;

           12  -6   -6

     

 

            18    3    6                                

  _x=   6   -3   -3   ≠ 0;

            18  -6   -6

            

 

             9   18  6

_y =    6   6   -3    ≠ 0;

            12  18  -6 

 

   9    3   18

_z =   6   -3   6    ≠ 0;

           12  -6  18

 

 = 0; _х  ≠ 0, або _у  ≠ 0 або _z  ≠ 0 - система розв’язків не має

Відповідь: Система розв’язків не має.

 

 

 

 

 

 

 

 

№ 3. Розв’язати систему лінійних рівнянь.

      2x - 5y + z = -2;

     4x + 3y - 6z = 1;

     2x + 21y - 15z =8;                                     

      

            2   5   1

 =    4   3  - 6   = 0;

           2  21 - 15                                   

 

           -2   -5   1                                

_x=   1    3   -6   = 0;

           8   21 -15

            

            2  -2   1

_y =   4   3   -6    = 0;

            2  21 -15 

 

    2   5  -2

_z =    4   3    1    = 0;

             2  21   8

 

 = _х  = _у  = _z  = 0 – система має безліч розв’язків

 

Відповідь: Система має безліч розв’язків.

 

 

 

 

 

 

 

Розділ VI Приклади для самостійного розв’язування.

          2x - 2у – z =3;

1.       3х + 4у - 5z = 1;

         -5х – 4у + 3z = -15;

 

    

          4x + 4у + z = -27;

2.       -5х + 5у + 4z = -1;

          2х – у - 3z = -5;

 

 

          -4x - 4у + 2z = -12;

3.       -5х + 4у + 5z = -22;

          -2х + 3у - z = -9;

 

 

          2x - у + 5z = -2;

4.       4х + у + 5z = 12;

          4х - 4у - 5z = 22;

 

  

          4x + у - 3z = -34;

5.       -5х - 2у + 2z = 41;

          2х - 4у - 3z = 1.

 

 

 

 

 

 

 

Висновок

 Отже можна зробити такий висновок, що системи лінійних рівнянь з трьома невідомими  можна розв’язувати такими методами: Крамера, Гаусса, матричним методом.

 Всі ці методи єднає одна схожа система розв’язку. Наприклад при матричному способі розв’язку за теоремою про зміщення кожний елемент останньої матриці дорівнює значенням допоміжних визначників х, у, z, які були введені при розв’язуванні систем за формулами Крамера.

 Метод Гаусса досить зручний для розв’язування вручну систем лінійних рівнянь з невеликою кількістю невідомих. Він з успіхом може бути використаний також для розв’язування лінійних систем на ЕОМ.  

 Матричний метод зручний тим, що у нього досить зрозумілий та простий алгоритм розв’язання.

Метод Крамера найбільш простий при застосуванні схем, за якими можна обчислювати визначники третього порядку.

 Всі ці методи досить зручні та цікаві, користуючись ними, я навчилась, розв’язувати системи лінійних рівнянь з трьома невідомими іншими способами, а не традиційними, які ми вивчаємо в школі.

 

 

 

 

Список використаної літератури

1. Гудименко Ф. С., Борищенко Д. М., Волкова В. О., Ющенко О. А.  Збірник задач з вищої математики. К., 1967.

2. Горделадзе Ш. Г., Кухарчук М. М., Яремчук Ф. П. Збірник конкурсних задач з математики. – К., 1998.

3. Дубовик В. П., Юрик І. І., Вища математика: Навчальний посібник – К.: Видавництво А. С. К., 2003. – 684 с.

4. Курош А. Г. Курс вищої алгебри. – К., 1990.

5. Барановська Г. Г., Ясінський В. В. Практикум з математики. Алгебра: На допомогу абітурієнту. – К.: Київська правда, 1997.