Урок "Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції. Розв’язування вправ."
Тема уроку. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції. Розв’язування вправ.
Мета уроку: формування знань учнів про поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів виконувати дії для знаходження названих властивостей функцій. За допомогою вивчених означень та вироблених умінь дослідити відомі учням елементарні функції на предмет проміжків зростання та спадання.
Тип уроку: формування знань, умінь та навичок.
Наочність та обладнання: презентація, роздатковий матеріал (індивідуальні аркуші із завданнями для самостійної роботи, різнокольорові ручки (зелена, синя, червона, фіолетова, коричнева), заготовки для відшукання властивостей елементарних функцій), Інтернет (блог вчителя математики та он-лайн програма LearningApps), набір демонстраційного креслярського приладдя, опорний конспект.
Хід уроку
I. Організаційний етап
— вступне слово вчителя:
Доброго дня, шановні учні! Ще 2400 років тому китайський педагог Конфуцій сказав:
„Те, що я чую , я забуваю.
Те, що я бачу і чую, я трохи пам'ятаю.
Те, що я чую, бачу і обговорюю, я починаю розуміти.
Коли я чую, бачу, обговорюю й роблю, набуваю знань і навичок.”

Тож закликаю вас до співпраці!
- але на початку уроку я хочу, щоб ви продемонстрували свій настрій на подальшу роботу на уроці, шляхом обрання однієї з поданих кольорових ручок, відповідно якими ви і будете працювати цілий урок. Кожен колір розшифровує ваш настрій. (рефлексія)
II. Перевірка домашнього завдання
Перевірку виконання письмових вправ провести у формі самоперевірки за зразком. (слайд )

III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Після перевірки виконання домашнього завдання та корекції можливих помилок ви усвідомлюєте необхідність подальшої роботи із закріплення як знань, так і вмінь по даній темі, які були сформовані на попередньому уроці.
Отже, метою нашого уроку є:
- формування знань учнів про поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку;
- знайти способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично;
- закріпити вміння учнів виконувати дії для знаходження названих властивостей функцій;
- за допомогою вивчених означень та вироблених умінь дослідити відомі учням елементарні функції на предмет проміжків зростання та спадання.

Таким чином, виділяємо два основні напрямки роботи на уроці, тобто формулюємо основні завдання на урок:
- закріпити знання та вміння основних понять, набутих на попередньому уроці (слайд хмара тегів) — виділіть самостійно основні поняття нашого уроку;

- за допомогою цих знань та вмінь дослідити елементарні функції, та записати отримані висновки у вигляді опорних тверджень.
Отож, летимо формувати ваші знання, уміння та навички.
ІV. Актуалізація опорних знань
Слайд посилання на блог вчителя (інтернет-програма LearningApps)
По горизонталі:
- Якщо більшому значенню аргументу відповідає менше значення функції, то функція - … (спадає)
- Як називається прилад, який сам викреслює графіки функцій? (кардіограф)
- Незалежна змінна. (аргумент)
По вертикалі:
- Якщо більшому значенню аргументу відповідає більше значення функції, то функція… (зростає)
- Процеси і явища повторюваного характеру. (періодичність)
- Чим частіше всього задають функціональні відповідності? (формулою)
- Яке слово у логіці розуміють під словом доказ, підстава? (аргумент)
- Значення аргументу, для яких значення функції дорівнює 0 - це .... функції (нулі)
- Якщо виконується рівність f(-x)=f(x), то функція ... (парна)
- Графік парної функції ... відносно осі у (симетричний)
- Якщо виконується рівність f(-x)=-f(x), то функція ... (непарна)
Кросворд

V. Формування умінь та навичок учнів.
Розвязування вправ. Колективна робота
Зміст вправ, які планується розв'язати на даному уроці, майже такий самий, що і зміст вправ попереднього уроку:
- знайти нулі, проміжки знакосталості, проміжки зростання та проміжки спадання деякої функції, заданої графічно;
- за допомогою обчислень знайти нулі функції, заданої формулою y = f(x);
- за допомогою обчислень визначити, зростає чи спадає дана функція на заданому проміжку.
«Розминка» (усно):
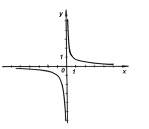
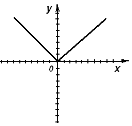
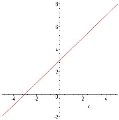
- Знайдіть нулі функції, проміжки спадання, зростання та проміжки знакосталості функції згідно даного графіка:
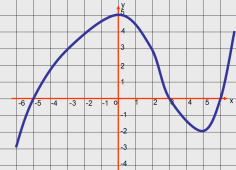 нулі:
нулі: ![]()
додатні: ![]()
від’ємні: ![]()
спадає: ![]()
зростає: ![]()
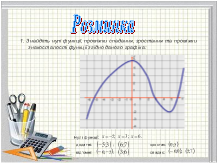
- Згідно даного графіка визначіть чи функція парна чи непарна.
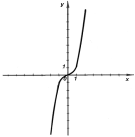

Письмові вправи
№265(б, в)
Запитання:
- Як знайти нулі функції, якщо вона задана формулою?
- Коли дробовий вираз дорівнює 0?
- Отже, ми прирівнюємо до нуля …?
Знайдіть нулі функції:
![]()
![]()
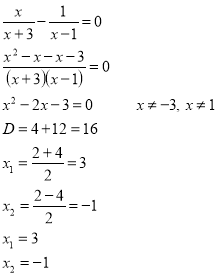
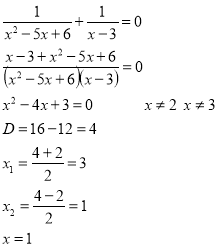

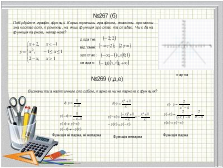
№267(б)
Запитання:
-
На скільки частин умовно поділимо нашу вісь
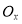 ?
?
-
Графіком функції
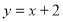 буде…
буде…
-
Графіком функції
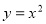 буде…
буде…
-
Графіком функції
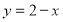 буде…
буде…
Побудуйте графік функції. Користуючись графіком, вкажіть: проміжки знакосталості, проміжки, на яких функція зростає та спадає. Чи є дана функція парною, непарною?
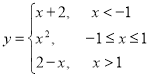

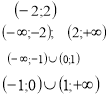 Функція парна
Функція парна 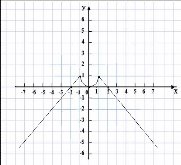
№269(г, д, е)
Запитання:
- Яка функція називається парною; непарною.
-
Отже, знаходимо
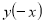 .
.
Визначити аналітичним способом, парною чи непарною є функція?
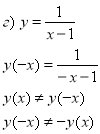
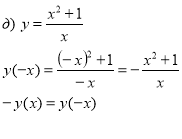
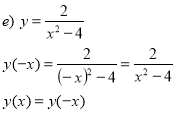
Ні парна, ні непарна непарна парна
Проте до названих вправ додаємо вправи на дослідження елементарних функцій (лінійної, оберненої пропорційності, квадратичної функції та функції у = ![]() ), знайомих учням із 7 та 8 класів, на зростання та спадання, а також на проміжки знакосталості. Результати цих досліджень продемонструвати на екрані.
), знайомих учням із 7 та 8 класів, на зростання та спадання, а також на проміжки знакосталості. Результати цих досліджень продемонструвати на екрані.
Отримані відповіді записати на відповідних листках.

VI. Перевірка знань, умінь та навичок.
1. Самостійна робота із взаємоперевіркою.
Текст самостійної роботи поданий у додатку 1

2. Взаємоперевірка результатів.
І варіант: А; В; Б; Г; А; А; В; В; Б; В; Б; А.
ІІ варіант: Б; Г; Б; А; Г; Б; Г; А; А; Б; А; Б.

VIII. Пояснення домашнього завдання
- Вивчити зміст означень, розглянутих на попередньому уроці, та виділені на цьому уроці властивості елементарних функцій (2 п. 8, 9).
- Розв'язати вправи на застосування вивчених означень та фактів.
№ 266,268 додатково №270
- Повторити зміст поняття «графік функції».

IX. Підсумки уроку

-
Дякую. Досить змістовно


про публікацію авторської розробки
Додати розробку
