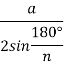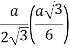Навчальний посібник "Геометрія 9 клас ІІ семестр"

Про матеріал

Посібник розроблений згідно Комбінованої системи М.П. Гузика і може бути використаний як додатковий матеріал для учнів на уроки. Кожна тема посібника має таку структуру: - перший урок – урок розбору блоку навчальної інформації; - наступні уроки – уроки фронтального опрацювання матеріалу, - між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу; - в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.

Перегляд файлу

Блок №4. Правильні многокутники

Урок №1

Правильні многокутники

«Математик, подібно до художника чи поета, -

творець форм… Перше випробування – краса»

Г. Харді

Питання

Правильні многокутники.
Довжина кола. Площа круга.

Література

Істер О.С. Геометрія: Підручник для 9 класу, §15 – 17, стор. 139 – 168.

1. Правильні многокутники

1.1

Многокутник називається правильним, якщо у нього всі сторони рівні і всі кути рівні між собою.

1.2

Кут правильного n – кутника обчислюється за формулою

=120⁰

1.3

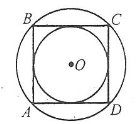
Теорема (властивість правильного многокутника)

Якщо многокутник правильний, то навколо нього можна описати коло і в нього можна вписати коло.

1.4

У правильному многокутнику центри вписаного і описаного кіл збігаються. Спільний центр цих кіл називається центром правильного многокутника.

1.5

Перпендикуляр, проведений з центра правильного многокутника до його сторони, називається апофемою цього многокутника. Апофема є радіусом вписаного кола.

1.6

Кут, утворений двома радіусами, проведеними у суміжні вершини правильного многокутника, називається його центральним кутом.

1.7

Центральний кут правильного многокутника обчислюється за формулою:

1.8

Формули радіусів вписаних і описаних кіл

n = 3

n = 4

n = 6

2. Довжина кола. Площа круга

2.9

Відношення довжини кола до його діаметра одне й те саме для кожного кола.

2.10

Довжина кола, площа круга

- довжина кола

- довжина дуги кола

– площа круга

2.11

Круговим сектором називається частина круга, обмежена двома радіусами і дугою.

2.12

Площа сектора:

2.13

Круговим сегментом називається частина круга,обмежена хордою і дугою

2.14

Площа кругового сегмента дорівнює різниці площі сектора круга і площі трикутника.

Урок №2

«Бог найвищий у силі Своїй, -

хто навчає, як Він?»

Йова 36:22

Фронтальне опрацювання матеріалу

Формули радіусів вписаних і описаних кіл правильних многокутників

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.8 блоку № 4.
Закінчи речення:

Правильним називається многокутник у якого...
Градусна міра кута правильного многокутника дорівнює...
Правильний трикутник – це…
Його кут дорівнює...
Правильний чотирикутник – це...
Його кут дорівнює...
Кожен кут правильного шестикутника має величину...
Сторона правильного шестикутника дорівнює...

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 2.

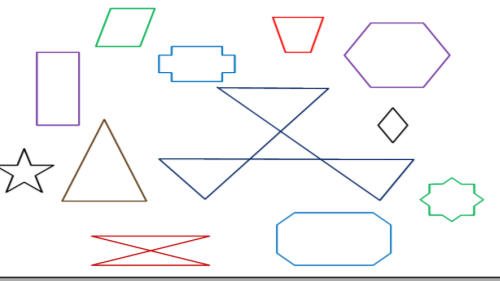
1) Скільки на малюнку є не опуклих многокутників?

2) Які з запропонованих фігур не є опуклими многокутниками та чому?

Завдання 3.

Виконай письмово вправи:

3.1. Обчисліть кут правильного n-кутника, якщо: 1) n = 5; 2) n = 12; 3) n = 18.

3.2. Знайдіть центральний кут правильного n-кутника, якщо: 1) n = 20; 2) n = 24; 3) n = 10.

3.3. Знайдіть кут правильного n-кутника, якщо його зовнішній кут дорівнює: 1) 60°; 2) 26°; 3) 34°.

3.4. Знайдіть кількість сторін правильного n-кутника, якщо його кут дорівнює: 1) 135°; 2) 150°; 3) 140°.

Завдання 4.

Виконай письмово вправи стор. 147 підручника: 745, 746.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 5.

Усно дай відповідь на питання:

Чому бджоли «вибрали» собі для комірок форму правильного шестикутника?

Урок №3

«бо Господь дає мудрість,

з Його уст – знання й розум!»

Книга Приповістей Соломонових 2:6

Фронтальне опрацювання матеріалу

Довжина кола. Площа круга. Практичні задачі

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори блок № 4.
Усно дай відповідь на питання:

Який многокутник називається правильним?
Чому дорівнює градусна міра кута правильного многокутника?
Яку властивість має правильний многокутник?
Що називають центром правильного многокутника?
Що таке апофема правильного многокутника?
Що називають центральним кутом правильного многокутника? Чому він дорівнює?
Що таке число π?
Як записуються формули довжини кола, довжини дуги, площі круга?

Завдання 2.

Практична робота

Намасти нитку клеєм і наклади її на коло так, як показано на малюнку.

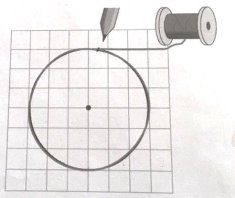
$C:\Users\алло\Desktop\viber image.jpg$

Зроби на нитці позначку або відріж нитку там, де вона збіглася зі своїм кінцем.
Відклей нитку і за допомогою лінійки виміряй її довжину. … У такий спосіб ти виміряв (виміряла) довжину кола.

$C:\Users\алло\Desktop\viber image.jpg$

Виміряй діаметр цього кола. …

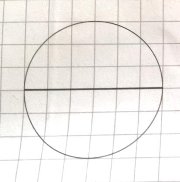
$C:\Users\алло\Desktop\viber image.jpg$

Знайди відношення довжини кола до його діаметра. …
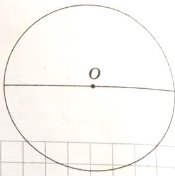
Виконай такі ж вимірювання для зображених кіл.

$C:\Users\алло\Desktop\viber image.jpg$ $C:\Users\алло\Desktop\viber image.jpg$

Порівняй відношення у пунктах 5 і 6. Запиши висновок.

$C:\Users\алло\Desktop\viber image.jpg$

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Виконай письмово вправи:

$C:\Users\алло\Desktop\IMG_0015.jpg$ $C:\Users\алло\Desktop\IMG_0017.jpg$ 3.1. Підприємство – виробник овочевих консервів – замовило етикетку для банок зі своєю продукцією. Відомо, що діаметр дна банки дорівнює 10 см. Знайди довжину етикетки.

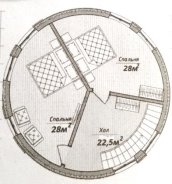
3.2. Визнач за планом квартири довжину міжкімнатних стін.

3.3. Щоб засіяти газону, потрібно 20 г насіння трави. Кілограм такого насіння коштує 350 грн. Скільки грошей потрібно витратити на насіння, щоб засіяти травою круглу ділянку, радіус якої 20 м?

3.4. Бабуся хоче пошити скатертину на круглий стіл, діаметр якого дорівнює 1,6 м.

$C:\Users\алло\Desktop\IMG_0016.jpg$

Визнач:

Чи вистачить тканини розміром ?
Чи може діаметр цієї скатертини дорівнювати 1,6 м?
Яким має бути радіус скатертини, щоб вона звисала зі столу на 20 см?
Скільки тканини бабуся витратить на пошиття скатертини, яка звисатиме на 20 см?
Якого розміру відріз тканини потрібно купити бабусі?
Скільки тканини піде на відходи, якщо бабуся купить тканину розміром ?

Урок №4

«бо Господь дає мудрість,

з Його уст – знання й розум!»

Книга Приповістей Соломонових 2:6

Фронтальне опрацювання матеріалу

Довжина кола. Площа круга та його частин

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори блок № 4.
Усно дай відповідь на питання:

Який многокутник називається правильним?
Чому дорівнює градусна міра кута правильного многокутника?
Яку властивість має правильний многокутник?
Що називають центром правильного многокутника?
Що таке апофема правильного многокутника?
Що називають центральним кутом правильного многокутника? Чому він дорівнює?
Що таке число π?
Як записуються формули довжини кола, довжини дуги, площі круга?

Завдання 2.

Усно виконай вправи:

Серед наведених формул вкажи формулу площі круга радіуса R.

А	Б	В	Г

Знайди градусну міру кута правильного п’ятнадцятикутника.

А	Б	В	Г
100⁰	156⁰	110⁰	120⁰

Знайди довжину кола з радіусом 4 см.

А	Б	В	Г
2π см	4π см	π см	6π см

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Виконай письмово вправи:

Знайди площу круга радіусом 4 см.
Площа круга дорівнює 72π см². Знайди довжину дуги, що обмежує круговий сектор, площа якого дорівнює 66π см ².
Знайди відношення довжини кола, описаного навколо правильного чотирикутника, до довжини кола, вписаного в нього.
Знайди радіус кола, вписаного у правильний трикутник, периметр якого дорівнює см.
Знайди периметр правильного трикутника, якщо радіус описаного кола дорівнює 3 см.

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

Знайди площу круга радіусом 5 см.
Знайди радіус кола, вписаного у правильний чотирикутник, периметр якого дорівнює 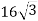см.
Знайди периметр правильного трикутника, якщо радіус описаного кола дорівнює 2 см.
Площа круга дорівнює 72π см ². Знайди довжину дуги, що обмежує круговий сектор, площа якого дорівнює 66π см ².
Знайди відношення довжини кола, описаного навколо правильного трикутника, до довжини кола, вписаного в нього.

Урок №6

«О, коли б ми в ганебних справах були такі ж соромливі і боязкі,

як це часто ми буваємо боязкі і хибно соромливі у порядних вчинках!»

Григорій Сковорода

Внутрішньопредметне узагальнення матеріалу

Правильні многокутники

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 4.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно виконай вправи:

Знайди центральний кут правильного 72-кутника.

А	Б	В	Г
15º	12º	5º	100º

Знайди градусну міру кута правильного 36-кутника.

А	Б	В	Г
120⁰	170⁰	36⁰	58⁰

Знайди площу круга, радіус якого дорівнює 3 см.

А	Б	В	Г
3π см ²	9π см ²	6π см ²	8π см ²

Завдання 3.

Письмово виконай вправи:

Знайди площу круга, якщо довжина кола,що його обмежує, дорівнює 12 см.
Знайди градусну міру дуги кола, радіус якого становить 20 см, а довжина дуги дорівнює 4 см.
Знайди довжину кола, вписаного у правильний шестикутник, периметр якого дорівнює см.
Довжина кола, описаного навколо правильного трикутника, дорівнює 12 см.Знайди периметр трикутника.
Навколо квадрата зі стороною 4 см описано коло, навколо кола описано правильний шестикутник, навколо якого описано ще одне коло. Знайди радіус цього кола.
Навколо правильного шестикутника зі стороною 3 см описано коло, навколо кола описано правильний трикутник, навколо якого описано ще одне коло. Знайди радіус цього кола.
Навколо правильного трикутника зі стороною см описано коло, навколо кола описано правильний шестикутник, навколо якого описано ще одне коло. Знайди радіус цього кола.

Урок №8

Творчий залік

Створення розповіді за методом сторітелінгу

Сторітелінг (storytelling) – це мистецтво розповідати історії з метою навчання, керування шляхом донесення змісту повідомлення за допомогою спеціальної методики.

Ваше завдання – створити розповідь або казку про основні геометричні фігури, відомі вам, використовуючи метод сторітелінгу.

Щоб її створити, вам потрібно чітко знати тему, розробити сюжет, вигадати непересічного героя, додати трохи цікавих подій та вивести правильні висновки. В цілому алгоритм дій буде наступним:

Визначення теми та мети розповіді – від цього залежить вибір сюжету історії.
Розробка детального сюжету та основних подій оповіді.
Вибір головного героя – подумайте над його іменем, характером, зовнішністю тощо.
Вигадка інтриги (чим більш несподіваною вона буде, тим краще!). На цьому етапі вже можна складати перший варіант історії.
Прочитайте готовий варіант та додайте метафори.

Історія може бути вигаданою від початку і до кінця, але також можна використовувати цілком реальні події. Так буде навіть краще, адже випадки з життя завжди викликають величезну цікавість. Зверніть увагу: розповідь має бути емоційною та динамічною, події мають йти одна за одною. Також ви повинні розкрити основні означення, властивості геометричних фігур.

Приклад історії:

На схилі років сер Ісаак Ньютон розповів, як саме йому вдалося відкрити закон всесвітнього тяжіння. Так, у цій історії знайшлося місце яблуку. Ні, воно не падало великому вченому на голову.

Ньютон вже не перший рік працював над законами руху та розмірковував над тим, що твердження про існування окремо земної та небесної гравітації, можливо, є не самим правильним варіантом. Але що тоді правильно та як представити свої міркування у вигляді формул? Відповіді у Ньютона не було аж до того самого дня, коли у його життя втрутився його величність випадок.

Заходячи якось ввечері до батьківського саду, Ісаак Ньютон навіть не здогадувався, чим завершиться ця прогулянка. Навіть розглядаючи місяць, який з’явився на небі задовго до приходу ночі, він не думав про особливості гравітації. Але коли поруч з ним впало красиве соковите яблуко, все стало зрозуміло. Ньютон зробив цілком правильне припущення, що, можливо, це одна й тама сама сила змушує яблуко падати на землю, а Місяць – залишатися на орбіті.

Ці висновки були революційними. Саме тоді було покладено край розділенню Землі та Всесвіту.

Блок №5. Геометричні переміщення

Урок №1

Геометричні переміщення

«Натхнення потрібне в поезії, як і в геометрії»

О.С. Пушкін

Питання

Переміщення та його властивості. Рівність фігур
Симетрія відносно точки і прямої. Поворот. Паралельне перенесення.

Література

Істер О.С. Геометрія: Підручник для 9 класу, §18 – 22, стор. 169 – 194.

1. Переміщення та його властивості
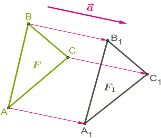
1.1	Перетворенням фігури F у фігуру називається така відповідність, за якої: 1) кожній точці фігури F відповідає певна точка фігури; 2) кожній точці фігури відповідає деяка точка фігури F; 3) різним точкам фігури F відповідають різні точки .
1.2	Переміщенням (рухом) називається таке перетворення однієї фігури в іншу, під час якого зберігається відстань між точками.
1.3	Властивості переміщення: 1) при переміщенні точки, що лежать на прямій переходять у точки, що лежать на прямій, і зберігається порядок їх взаємного розташування; 2) переміщення прямі переводить у прямі, промені – у промені, відрізки – у рівні їм відрізки; 3) переміщення переводить кут у рівний йому кут.
1.4	Дві фігури називаються рівними, якщо вони при переміщенні переходять одна в одну.
2. Симетрія відносно точки і прямої. Поворот. Паралельне перенесення.
2.5	Дві точки та називаються симетричними відносно точки О, якщо О є серединою відрізка .
2.6	Перетворення, при якому кожна точка фігури переходить у симетричну їй точку відносно даної точки О, називається перетворенням симетрії відносно точки О (центральна симетрія).
2.7	Точки *(a; b)* і *(– a; – b)* симетричні відносно початку координат.
2.8	Дві точки іплощини називаються симетричними відносно прямої l, якщо ця пряма перпендикулярна до відрізка і проходить через його середину.
2.9	Перетворення, при якому кожна точка фігури переходить у симетричну їй точку відносно даної прямої, називається симетрією відносно прямої (осьова симетрія).
2.10	Дві точки є симетричними: 1) відносно осі ОХ, якщо їх координати (a; b) і (a; – b); 2) відносно осі ОУ, якщо їх координати (a; b) і (– a; b); 3) відносно прямої y = x, якщо їх координати (a; b) і (b; а).
2.11	Поворотом навколо точки О на кут називають перетворення, при якому точка А переходить у точку так, що , і . О – центр повороту, α – кут повороту.
2.12	Перетворення, при якому всі точки фігури зміщуються в одному й тому самому напрямі на одну й ту саму відстань, називається паралельним перенесенням.
2.13	У прямокутній системі координат паралельне перенесення, яке переводить точку (х; у) у точку (; ) задається формулами: *= х + а,* *= у +* b, де а і b – деякі числа, одні й ті самі для заданого паралельного перенесення.
2.14	Теорема. Перетворення симетрії відносно точки, перетворення симетрії відносно прямої, поворот і паралельне перенесення є переміщенням.

Урок №2

«Глядіть, щоб ніхто нікому не віддавав злом за зло,

але завжди дбайте про добро один для одного й для всіх!»

1послання ап. Павла до солунян 5:15

Фронтальне опрацювання матеріалу

Переміщення та його властивості

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 1.4 блоку № 5.
Усно дай відповідь на питання:

Що називають перетворенням фігур?
Яке перетворення фігури називають переміщенням?
Назви основні властивості переміщення.
Під час переміщення точки А, В і С переходять відповідно у точки 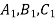. Точка С лежить між точками А і В. Яке взаємне розміщення точок ?
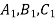В яку фігуру переходить під час переміщення промінь?
В яку фігуру переходить під час переміщення відрізок довжиною 3 см?
Які фігури називаються рівними?

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Виконай письмово вправи, стор. 173 – 174 підручника: 889, 891, 895, 900, 901.

Урок №3

«Люди – єдині істоти на землі,

які потребують допомоги Бога,

але ведуть себе так, ніби Бога немає»

Джоні Депп

Фронтальне опрацювання матеріалу

Симетрія відносно точки і прямої

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.10 блоку № 5.
Усно дай відповідь на питання:

Що називають перетворенням фігур?
Яке перетворення фігури називають переміщенням?
Назви основні властивості переміщення.
Які фігури називаються симетричними відносно точки?
Дайте визначення центральній симетрії.
Які фігури називаються симетричними відносно прямої?
Дайте визначення симетрії відносно прямої.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Усно виконайте вправи:

Чи є дані точки симетричними?

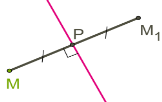
Яка симетрія зображена на малюнках?

1-web

3938 0129

Завдання 2.

3.1. Письмово виконайте вправи стор. 177: 909, 914, 919 (1).

3.2. Письмово виконайте вправи стор. 183: 932, 937 (1), 941.

Урок №4

«Всі хочуть змінити світ,

але ніхто не хоче змінитися сам»

Л. М. Толстой

Фронтальне опрацювання матеріалу

Поворот

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.11 блоку № 5.
Усно дай відповідь на питання:

Що називається перетворенням фігури F у фігуру ?
Що називають переміщенням або рухом?
Сформулюй властивості переміщення.
Які точки називаються симетричними відносно даної точки?
Що називають центральною симетрією?
Які точки називають симетричними відносно прямої?
Що називають осьовою симетрією?
Що називають поворотом?
1. Запам’ятайте правила для повороту. Допишіть їх у ваш блок.

Якщо точка В(х₁; у₁) є образом точки А(х; у) при повороті на 90° відносно початку координат:

а) за годинниковою стрілкою, то виконується умова

б) проти годинникової стрілки, то виконується умова

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Усно виконай вправи 949, 951, стор. 187 підручника.

Завдання 3.

Письмово виконай вправи, стор. 187, 188 підручника: 953, 955, 957, 959.

Урок №5

«Тільки дотримуючись законів геометрії,

архітектори давнини могли створити свої шедеври…

Минули століття, але роль геометрії не змінилась.

Як і раніше вона залишається граматикою архітектора»

Ле Корбюзьє

Фронтальне опрацювання матеріалу

Паралельне перенесення

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези блоку № 5.
Усно дай відповідь на питання:

Що називається перетворенням фігури F у фігуру ?
Що називають переміщенням або рухом?
Сформулюй властивості переміщення.
Які точки називаються симетричними відносно даної точки?
Що називають центральною симетрією?
Які точки називають симетричними відносно прямої?
Що називають осьовою симетрією?
Що називають поворотом?
Яке перетворення називають паралельним перенесенням?
Запишіть на дошці формули паралельного перенесення.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Усно виконай вправи 974, стор. 191 підручника.

Завдання 3.

3.1. Письмово виконати вправу 980, стор. 192 підручника.

Паралельне перенесення задано формулами . Знайдіть координати: 1) точки, в яку переходить точка ;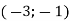

2) точки, образом якої є точка .

Чи існує паралельне перенесення, внаслідок якого точка переходить у точку , а точка у точку ?
Паралельне перенесення задано формулами . Знайдіть координати точки:

1) в яку переходить центр кола ;

2) образом якої є точка перетину прямих .

Задайте формулами паралельне перенесення, внаслідок якого точка (8; 3) переходить у середину відрізка з кінцями .

$C:\Users\секретар\Desktop\3b2435b942b6943beaaf-1.jpg$ Готуємось до індивідуального опрацювання матеріалу

Дано точку А 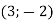. Побудуй симетричну їй точку відносно точки В .
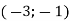Паралельне перенесення задано формулами . В яку точку при цьому паралельному перенесенні перейде точка А ?
Виконай поворот відрізка АВ навколо точки О, яка йому не належить, на 60⁰ проти годинникової стрілки.
Запиши рівняння кола, в яке переходить коло 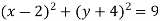при симетрії відносно осі абсцис.
Дано точки Чи існує переміщення, при якому відрізок ВС переходить у відрізок KL?

Урок №7

«О, коли б ми в ганебних справах були такі ж сором’язливі і боязкі,

як це часто ми буваємо боязкі і хибно сором’язливі у порядних вчинках!»

Григорій Сковорода

Внутрішньопредметне узагальнення матеріалу

Геометричні переміщення

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 5.
Дай письмово відповідь на питання, запропоновані вчителем.

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 2.

Усно виконай вправи:

Знайдіть координати точки О, відносно якої симетричні точки

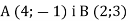
А	Б	В	Г

Серед точок виберіть дві, які симетричні відносно осі абсцис.

А	Б	В	Г
А і В	А і С	В і С	С і D

Серед наведених геометричних фігур вкажіть ту, яка не має осей симетрії.

А	Б	В	Г
Прямокутник	Паралелограм	Коло	Відрізок

Завдання 3.

Письмово виконай вправи:

При паралельному перенесенні точка переходить у точку . Знайдіть координати точки , у яку переходить точка при цьому паралельному перенесенні.
Сторони трикутника дорівнюють 6 см, 8 см, 12 см. Знайдіть найбільшу сторону подібного йому трикутника, якщо його найменша сторона дорівнює 18 см.
Виконайте поворот трикутника АВС навколо точки С на 60⁰ проти годинникової стрілки.
Дано відрізок з кінцями у точках . Побудуйте відрізок, симетричний відрізку АВ відносно початку координат, та знайдіть координати його кінців.
При паралельному перенесенні точка А переходить у середину відрізка з кінцями В 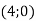, С 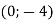. Записати рівняння кола, в яке при цьому паралельному перенесенні перейде коло.

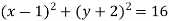Урок №9

Творчий залік

Все навколо – геометрія

Термін реалізації – 1 місяць

Кількість учасників – 15 учнів

Освітня галузь – «Геометрія». Тема – «Геометричні переміщення».

Перебіг роботи

Клас ділиться на 4 групи за бажанням і вподобанням учнів. У кожної групи є своє завдання, яке учні виконують на протязі терміну реалізації. Створеним групах необхідно на підсумковому занятті захистити свою роботу, представивши учням класу свою працю у вигляді підсумкового продукту – або презентації, або виготовленої роботи.

1 група «Дослідники»

Вам необхідно провести статистичне дослідження, чи існує симетрія у будові тіла людини і показати це на прикладі учнів вашого класу. Завдання для групи:

Знайти інформацію про середньостатистичні пропорційні параметри тіла людини (шия, плече, стегно, ікра, груди, бедра, талія);
Виміряйте параметри всіх членів вашої групи;
Складіть відповідні таблиці;
Зробіть аналіз на основі ваших даних, чи у кожного члена групи пропорційне тіло;
Результати досліджень подайте у вигляді таблиці, графіку, або діаграми.
Захистіть свій проект за допомогою презентації. Вашу роботу оформіть у брошуру.

Наприклад:

У даний час у нашій країні використовуються нормативи пропорційної статури жінки, складені ще в кінці 19 століття доктором А. К. Анохіним. Згідно з цими нормативами, на 1 см зросту жінки має припадати:

шия - 0,18-0,2 см;

рука (плече) -0,18-0,2 см;

нога (стегно) - 0,32-0,36 см (максимум);

нога (ікра) - 0,21-0,23 см;

груди (не погруддя) - 0,5-0,55 см і більше;

таз - 0,54 см (мінімум) - 0,62 см (максимум);

талія - 0,35-0,40 см

Помножте свій ріст (у сантиметрах) на вищенаведені цифри.

А потім проведіть відповідні вимірювання ваших частин тіла. За результатами зрозумієте, наскільки ви укладаєтеся в нормативи.

Нормативи пропорційної статури чоловіка відшукайте, використовуючи інтернет-ресурси.

2 група «Історичні фотографи»

Вам необхідно створити альбом старих і сучасних фотографій найвизначніших історичних архітектурних пам’яток Луцька та Ківерець.

На кожній фотографії відшукати вид геометричного переміщення: симетрія, поворот та ін., і показати це на фото.
Вашу роботу оформити у фотоальбом. Для захисту проекту використайте презентацію.

Наприклад:

$F:\Симетрія\Симетрия\IMG_2109.jpg$

3 група «Етнографи»

Вам необхідно відшукати геометричні переміщення у традиціях і побуті українського народу: у вишивці різних регіонів України, у писанках різних регіонів України, у старовинних українських будинках, у предметах українського побуту. Для захисту проекту використайте презентацію з малюнками та інформацію про зображене. Обов’язково виготовте на ваш вибір: або писанки, або зразки вишивки кожним учасником групи.

Безымянный.png

4 група «Драматурги»

Вам необхідно створити заготовки для лялькового театру-вертепу або пальчикового театру із фетру. За виготовленими заготовками виготовити кожну ляльку. Показати вид симетрії на кожній ляльці. Поставити казку із персонажів, виготовлених вами особисто. Регламент казки – від 5 до 10 хвилини.

5 група «Архітектори»

Вам необхідно створити скриню для того, щоб зберігати театральних героїв учасників групи 4. Скриня має форму прямокутного паралелепіпеда.

Потрібно скачати розгортку паралелепіпеда;
Зробити необхідні виміри;
Обчислити об’єм скрині.
Відповідно до властивостей симетрії розмістити у скрині предмети побуту героїв казки. Для цього вам необхідно порадитися з учасниками групи 4 про їхніх героїв, і відповідно до цього облаштувати їхній побут.

Повторення матеріалу, вивченого протягом року

Урок №1

«Математику неможливо вивчати,

спостерігаючи, як це робить сусід!»

Айвен Нівен, американський математик

Внутрішньопредметне узагальнення матеріалу за рік

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 1.

Усно виконай вправи:

Площа квадрата дорівнює 64 см ². Знайди площу ромба, сторона якого дорівнює стороні квадрата, а гострий кут – 30°.

А	Б	В	Г
128 см ²	64 см ²	32 см ²	32 см ²

Знайди площу трикутника, якщо його сторони дорівнюють 4 см, 5 см, 7 см.

А	Б	В	Г
	см ²	28 см ²	см ²

Запиши рівняння кола, радіусом 3 см та центром О (3; 2).

А	Б	В	Г

Завдання 2.

Письмово виконай вправи:

Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайди висоту трикутника, проведену до гіпотенузи.
Площа рівностороннього трикутника дорівнює 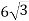см ². Знайди радіус кола, описаного навколо трикутника.
Проекції катетів на гіпотенузу відповідно дорівнюють 9 см і 3 см. Знайди менший катет трикутника.
Знайди площу ромба зі стороною 5 см, якщо різниця діагоналей дорівнює 2 см.
Довжини двох сторін трикутника, кут між якими дорівнює 120°, відносяться як 2 : 7, а третя сторона дорівнює 18 см. Знайди площу трикутника.

~ 1 ~

Середня оцінка розробки

Структурованість

4.0

Оригінальність викладу

4.0

Відповідність темі

5.0

Загальна:

4.3

Всього відгуків: 1

Оцінки та відгуки

Мазур Олена 27.03.2021 в 13:10

Загальна:

4.3

Структурованість

4.0

Оригінальність викладу

4.0

Відповідність темі

5.0

docx

Завантажити

Зберегти на потім

Додав(-ла)

Суворова Олеся Миколаївна

Пов’язані теми

Геометрія, 9 клас, Матеріали до уроків

До підручника

Геометрія 9 клас (Істер О. С.)

Додано

3 лютого 2019

Переглядів

7088

Оцінка розробки

4.3 (1 відгук)