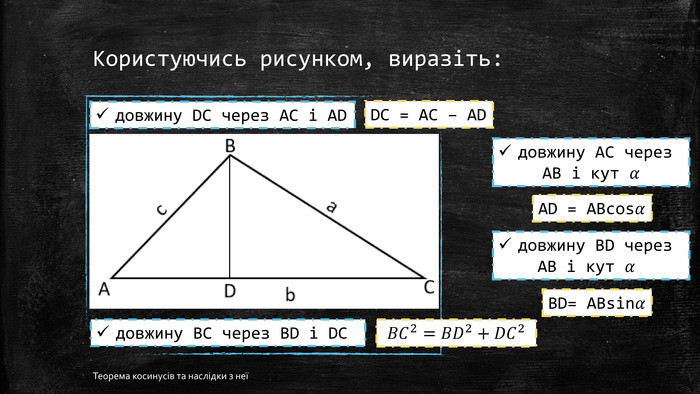
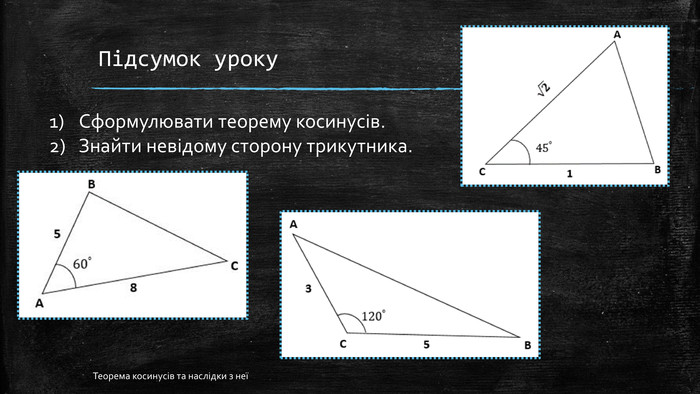
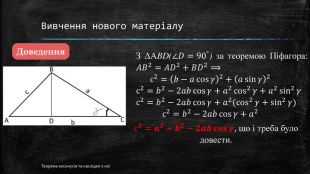
Презентація "Теорема косинусів та наслідки з неї"
Про матеріал
Презентація до уроку "Теорема косинусів та наслідки з неї" містить необхідний мінімум з даної теми, щоб закласти впевнений старт при вивченні даної теми. Основа є, і її можна використати для створення свого найкращого уроку! Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку