Навчальний посібник: "Практичні роботи з геометрії 7 клас"

УПРАВЛІННЯ ОСВІТИ

ВІННИЦЬКОЇ МІСЬКОЇ РАДИ

МІСЬКИЙ МЕТОДИЧНИЙ КАБІНЕТ

 

 

 

 

 

Практичні роботи з геометрії

для 7 класу

 

 

 

 

Ясевіна Тетяна Тимофіївна

вчитель математики, спеціаліст вищої кваліфікаційної категорії, старший вчитель

закладу «Середня загальноосвітня

школа І – ІІІ ступенів №4

ім. Д.І.Менделєєва м. Вінниці»

м. Вінниця вул. Гоголя, 18

т. 0432562445

 

 

 

 

 

м. Вінниця

2010 – 2011н.р.

Автор – укладач: Ясевіна Т.Т., вчитель математики закладу «Середня загальноосвітня школа І-ІІІ ступенів №4 ім. Д.І.Менделєєва м. Вінниці»

Практичні роботи з геометрії для 7 класу/Методичний посібник/Т.Т.Ясевіна. – Вінниця, 2011.- 79 с.

 

 

 

 

Рецензенти:

Ковальчук Л.А., методист з навчальних дисциплін міського методичного кабінету управління освіти Вінницької міської ради.

Радер М.Л., вчитель математики закладу «Середня загальноосвітня школа І-ІІІ ступенів №4 ім. Д.І.Менделєєва м. Вінниці», вчитель вищої кваліфікаційної категорії, вчитель – методист.

 

 

Рекомендовано науково – методичною радою

міського методичного кабінету

управління освіти Вінницької міської ради

(Протокол №        від                       )

 

 

 

 

Посібник укладено з урахуванням технології інтенсифікації навчання. Особлива увага приділяється практичній спрямованості курсу геометрії 7 класу. Посібник містить розробку 20 практичних робіт з геометрії 7 класу, згідно чинної програми.

Методичний посібник призначено для вчителів математики, студентів, а також для учнів загальноосвітніх шкіл.

 

 

ЗМІСТ

	ВСТУП		5
РОЗДІЛ І.  ЯК ПРАВИЛЬНО КОРИСТУВАТИСЯ КРЕСЛЯРСЬКИМ ПРИЛАДДЯМ			8
РОЗДІЛ ІІ. ПРАКТИЧНІ РОБОТИ			11
	Практична робота №1		11
	Практична робота №2		14
	Практична робота №3		17
	Практична робота №4		19
	Практична робота №5		22
	Приклад уроку з використанням практичної роботи		24
	Практична робота №6		27
	Практична робота №7		30
	Практична робота №8		33
	Практична робота №9		37
	Практична робота №10		39
	Практична робота №11		44
	Практична робота №12		47
	Практична робота №13		51
	Практична робота №14		53
	Практична робота №15		56
	Практична робота №16		58
	Практична робота №17		61
	Практична робота №18		63
	Практична робота №19		65
	Практична робота №20		67
РОЗДІЛ ІІІ. ПЕРЕВІР СВОЇ ЗНАННЯ			70
		Кросворд 1	70
		Кросворд 2	70
		Кросворд 3	71
		Кросворд 4	72
		Кросворд 5	73
		Відповіді до кросвордів	74
ВИСНОВКИ			75
ЛІТЕРАТУРА			76

 

 

 

Ясевіна Тетяна Тимофіївна –

вчитель математики закладу «Середня загальноосвітня школа І-ІІІ ступенів №4 ім. Д.І.Менделєєва м. Вінниці», вчитель вищої кваліфікаційної категорії, старший вчитель; класний керівник 8 – В класу, голова МО класних керівників 8 – 11 класів.

 

 

 

 

 

Педагогічне кредо:

«…Учитель повинен свідомо йти в ногу із сучасністю, пройматися й надихатися силами, що пробудилися в ній»

ВСТУП

«Світ, що нас оточує, - це світ геометрії.

Тож давайте його пізнавати»

Д. Гільберт

Геометрія надає вчителю унікальну можливість розвивати дитину на будь-якій стадії формування її інтелекту. Основні її складові (фігури, логіка і практичне застосування) дозволяють гармонійно розвивати образне й логічне мислення дитини будь-якого віку, виховувати у неї навички практичної діяльності.

Геометрія як наука допомагає оволодівати методами пізнання, науковим стилем мислення, просторовою уявою та уявленнями, математичною інтуїцією.

Для забезпечення якісної геометричної освіти школяра потрібно, щоб увесь курс шкільної геометрії був єдиним цілим. Вивчення систематичного курсу геометрії починається в 7 класі, але вже у 5-х, 6-х класах учні знають близько 40 геометричних понять.

Виконання практичних робіт з геометрії ( зокрема, планіметрії) надає учням можливість в значній мірі оволодіти наочно-інтуїтивним рівнем розвитку геометричного мислення з використанням елементів дедуктивного для успішного розвитку абстрактного логічного мислення в старших класах при вивченні стереометрії.

Через практичні роботи здійснюється діяльнісний підхід до навчання, який полягає в тому, що дитина повинна мислити і діяти, тобто конструювати, виготовляти, складати, виконувати побудови, моделювати і думати. Поступово від зовнішніх дій з матеріальними предметами учень переходить до мисленого оперування ними.

Структура пізнавальної діяльності учнів під час виконання практичних робіт з геометрії така:

1. Отримання навчально-практичного завдання.
2. Виконання практичного завдання.
3. Узагальнення результату, отриманого в процесі виконання практичної роботи.
4. Абстрагування, тобто формування геометричних понять.
5. Систематизація та інтерпретація геометричних знань.

За дидактичними функціями практичні роботи поділяються на навчальні, пізнавальні та перевірочні.

Ефективність пізнавальної діяльності учнів підвищується під час проведення навчальної практичної роботи, що для учнів є творчою. Виконання завдання й узагальнення отриманих результатів приводить їх до нового математичного поняття. За таких умов навчально-пізнавальна діяльність є розвиваючою, а нові знання не надходять ззовні, а є внутрішнім продуктом практичної діяльності учнів.

Перевірочні практичні роботи проводяться в тих випадках, коли потрібно визначити рівень знань учнів і закріпити теоретичні знання.

В процесі виконання практичної роботи може здійснюватися ознайомлення з новим теоретичним матеріалом (пізнавальні практичні роботи). Після введення нових понять шляхом узагальнення результатів практичної роботи подальший розвиток їх ґрунтується вже на досвіді, який мають учні.

В результаті виконання практичних робіт учні повинні отримати уявлення й оволодіти такими знаннями, вміннями і навичками:

1. Знати означення одних основних геометричних понять і отримати уявлення про інші;
2. Зображати знайомі фігури за їх описом;
3. Розрізняти відомі фігури і їх елементи на кресленнях, моделях і в оточуючих предметах;
4. Мати навички роботи з вимірювальними і креслярськими інструментами;
5. Вимірювати геометричні величини, виражати одні одиниці вимірювання через інші;
6. Виконувати побудови за допомогою даного набору креслярських інструментів; розв’язувати нескладні задачі, що зводяться до виконання основних побудов за допомогою лінійки і циркуля;
7. Обчислювати значення геометричних величин (довжин, кутів, площ, об’ємів), застосовуючи вивчені властивості і формули;
8. Проводити нескладні міркування і робити висновки у процесі розв’язування задач, передбачених програмою;
9. Користуватися геометричною символікою;
10. Встановлювати зв'язок геометричних фігур і їх властивостей з оточуючими предметами.

Після кожної практичної роботи подано 6 тренувальних вправ, розв’язування яких полегшить засвоєння і запам’ятовування вивченого.

Тренувальні вправи допомагають відпрацьовувати практичні вміння і навички учнів, які вони здобули в результаті виконання практичних робіт. Ці вправи можуть використовуватися як індивідуальні завдання при опитуванні, так і  в якості домашніх завдань.

Методика поєднання практичних  робіт і тренувальних вправ значно підвищує ефективність формування геометричних понять, допомагає учням «відчути» геометрію.

Практичні роботи з геометрії  - 7 надають можливість кожному учневі працювати самостійно, готуючись до Зовнішнього незалежного оцінювання із певних тем тоді, коли ці теми вивчаються.

РОЗДІЛ І

ЯК ПРАВИЛЬНО КОРИСТУВАТИСЯ КРЕСЛЯРСЬКИМ ПРИЛАДДЯМ

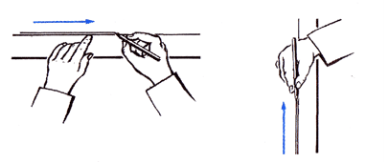
1. Підготовка олівця до роботи

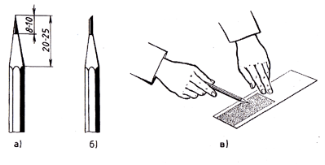
2.               Правильне положення рук і олівця під час роботи з лінійкою

3.        Підготовка циркуля до роботи

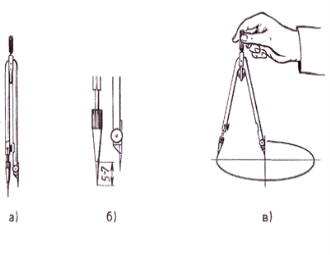
		1) Круговий циркуль.: використовується для проведення кіл середніх та великих діаметрів. В одній із ніжок він має олівцеву вставку, в іншій – голку (мал. а). Стержень олівцевої вставки повинен виходити назовні на 5 – 7 мм. В круговому  циркулі  ніжка
з олівцем  повинна бути дещо довша за ніжку з голкою, оскільки це полегшує проведення кіл (мал. б, в).

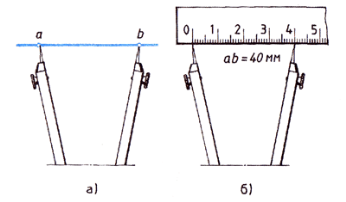
2.     Вимірний циркуль використовується для вимірювання, відкладення та поділу відрізків. Він має дві шарнірно з’єднані ніжки з голками (мал. а). Перед роботою з вимірним циркулем необхідно ніжки поставити на одному рівні (мал. б). Всі дії вимірним циркулем виконуються однією рукою.

4. Різновиди кутників. Перевірка наявності прямого кута в кутнику за допомогою лінійки.

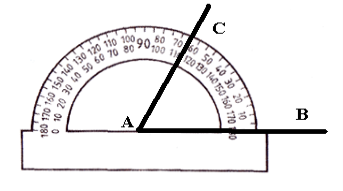
5. Транспортир – це інструмент для вимірювання та побудови кутів.

Кут ВАС дорівнює 65° - гострий.

Щоб виміряти кут ВАС треба прикласти транспортир так, щоб центр його співпав з точкою А, промінь АВ пройшов через початок відліку на шкалі. Тоді промінь АС вкаже на верхній шкалі градусну міру кута ВАС.

6. Готовальня з набором креслярського приладдя.

1 – пенал; 2 – олівцева ніжка до креслярського кронциркуля; 3 – подовжувач до креслярського циркуля; 4 - рейсфедер лінійний; 5 – кронциркуль з рейсфедером; 6 – викрутка; 7 – циркуль для розмітки; 8 – циркуль креслярський з олівцевою вставкою; 9 – ручка – подовжувач; 10 - рейсфедер лінійний; 11 – рейсфедер до креслярського циркуля; 12 – центрик; 13 – ніжка-голка до креслярського циркуля; 14 – вимірювач.

 

РОЗДІЛ ІІ

ПРАКТИЧНІ РОБОТИ

Практична робота №1

Тема: Точки і прямі, їх властивості.

Мета: навчитися зображати та знаходити на рисунках точки, прямі, позначати їх буквами; розглянути взаємне розміщення точок і прямих.

Обладнання: олівець, лінійка.

Хід роботи.

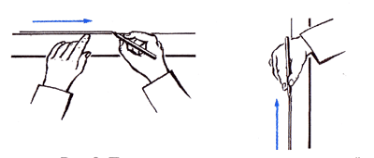
Вказівка. Щоб накреслити частину прямої, лінійку притримують і притискують до паперу, аби вона була нерухомою, чотирма розведеними пальцями (без великого). Рука має знаходитися ближче до середини лінійки. Олівець тримають у правій руці і злегка притискують до ребра лінійки і до паперу та трішки нахиляють у бік руху і від себе. Нігтьовий суглоб мізинця має ковзати по лінійці.

Мал. 1
А                                     В Мал. 2	Завдання І. Проведіть пряму лінію через ці точки. Спробуйте провести ще одну пряму через ці ж точки. Зробіть висновок.
а      В     М                    С Мал. 3	Завдання ІІ. На прямій а позначте ще декілька точок. Скільки всього точок можна позначити на одній прямій?
А   Мал. 4	Завдання ІІІ. Через точку А проведіть ще декілька прямих. Скільки всього прямих можна провести через одну точку?
Завдання IV. Накресліть пряму с. Позначте точку А, яка належить прямій с і точку В, яка не належить цій прямій. Проведіть пряму АВ. а) Яке взаємне розміщення прямих с і АВ? б) Чи завжди через точки А і В можна провести пряму? в) Скільки прямих можна провести через точки А і В. Чому?

 

 

 

 

Тренувальні вправи.

а                     М Мал. 1	Дано пряму а і точку М на ній (мал. 1). Проведіть пряму, що перетинає дану пряму в точці М. Скільки таких ліній можна провести?
С                               К   Мал. 2	Дано пряму b і точку С поза нею (мал.2). Через точку С проведіть пряму, що перетинає пряму  b в даній точці К, що лежить на b. Скільки таких прямих можна провести?
В     А             М               С                                     D Мал. 3	Знайти на мал. 3 а)прямі, які не проходять через точку А; б) прямі, які проходять через точку В; в) прямі, яким точка М не належить; г) прямі, які перетинаються в  точці С, але не проходять через точку А; д) довільні три точки, які не належать одній прямій.

4. Побудувати 5 прямих так, щоб вони утворювали п’ять точок перетину.
5. Побудувати прямі m  і n, точку О, яка належить даним прямим, точку Е, яка не належить даним прямим, точку К, яка належить прямій n і не належить прямій m.

B                     C   A                     Е                          D Мал. 4

Знайти точки перетину прямих (мал.4): 1) BC і DE; 2) CD і AB; 3) DE і AB; 4) AE і BC. Отримані точки перетину прямих позначте буквами О, М, Р, К.

 

Практична робота №2

Тема: Відрізок. Основні властивості вимірювання відрізків.

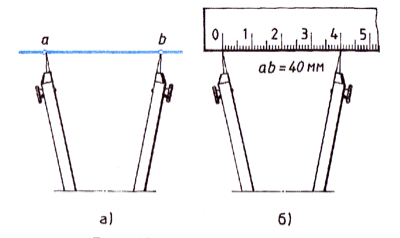
Мета: навчитися правильно вимірювати довжину відрізка за допомогою лінійки або циркуля. Перевірити виконання властивостей вимірювання відрізків.

Приладдя: олівець, лінійка, креслярський та вимірювальний циркуль.

Завдання І.

1. Проведіть пряму а.
2. Позначте на ній точки А і В.
3. Виміряйте відрізок АВ.
4. Позначте на відрізку АВ точку С.
5. Виміряйте відрізок АС і відрізок СВ.
6. Знайдіть суму довжин відрізків АС і СВ і порівняйте її з довжиною відрізка АВ. Який висновок можна зробити з цього порівняння?

Завдання ІІ.

Вказівка. Для вимірювання і відкладання відрізків можна користуватися як креслярським циркулем (у якого одна ніжка має вигляд голки, а друга закінчується олівцем), так і вимірним (у якого обидві ніжки закінчуються голками) (мал.1)

Мал.1

1. Порівняйте («на око» і циркулем ці відрізки) (мал. 2)

                                                            С

 

 

      А                        В                         D

Мал.2

2. Порівняйте («на око» і циркулем) (мал. 3) відстані між дзьобами першої та другої пташок з відстанню між дзьобами другої та третьої пташок. Зробіть висновок.

                                   

Мал. 3

3. На відрізку АВ позначте точку С, а на відрізку АС – точку D, який з відрізків більший: АD чи АВ? Поясніть чому.
4. Точка М належить відрізку АВ і точка К належить відрізку АВ. Точка М лежить між точками К і В. що довше: АМ чи АК?

Завдання ІІІ.

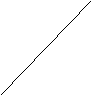
1. Назвіть усі відрізки, зображені на мал. 4.

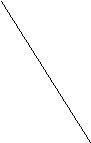
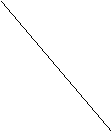
A                                                D                             T

                                            F           E                                 N    O          S

       B                   E                                  N    K

 

                C                                                M                            M

                                                                                      

Мал. 4

2. Знайдіть «на око» точку перетину відрізків АС і BD. Результат перевірити за допомогою лінійки (мал. 5).

      A                                    B

 

 

 

                  D                     C

Мал. 5

Тренувальні вправи

1. Чи може точка С лежати між точками А і В, якщо АВ=9 см і

1. АС=2 см, СВ=7 см
2. АС=2,7 см, СВ=6,4 см
3. АС=10 см, СВ=1 см?

2. Точка С належить відрізку АВ. АС=10 см, СВ=5 см. Знайти довжину відрізка АВ.
3. Точка М належить відрізку ВК, ВМ=15 см, ВК=26 см. Знайти довжину відрізка МК.
4. На відрізку АВ, довжина якого 42 см, взяли точку М. Знайти довжину відрізка ВМ, якщо АМ:ВМ=3:4.
5. На відрізку АВ, довжина якого 20 см, позначили точку М.

1. Відрізок АМ на 5 см довший МВ. Знайти довжини АМ і МВ.
2. Знайдіть відстань між серединами відрізків АМ і МВ.

6. Використовуючи малюнок 1 розв’язати задачі:

1. Дано: АВ=СD. Довести, що АС=ВD.
2. Дано: АС=ВD. Довести, що АВ=СD.

         

            А        В                                    С        D

                                       мал. 1

Практична робота №3

Тема: Відкладання відрізків і кутів.

Мета: навчитися відкладати відрізки та кути у заданій півплощині.

Приладдя: лінійка, олівець, вимірний циркуль.

Хід роботи.

1. Проведіть горизонтальну пряму, позначте на ній точки О і В;
2. На промені ОВ від його початкової точки відкладіть відрізок, що дорівнює 5 см;
3. Від променя ОВ у нижню півплощину відкладіть ∠ВОА=150º;
4. Скільки відрізків даної довжини можна відкласти на півпрямій від її початкової точки?
5. Скільки кутів даної величини можна відкласти від півпрямої у дану півплощину?

Тренувальні вправи.

1. Побудуй «на око» відрізки, довжини яких 3 см, 4 см,  6,5 см, що відкладені від точки А. Правильність побудови перевір лінійкою.
2. Побудуй «на око» кути, що дорівнюють 30º, 60º, 45º, 120º, відкладені від променя а. Правильність побудови перевір транспортиром.
3. Проведіть пряму а (горизонтально). Позначте у верхній півплощині точки А і В, а в нижній С і D. З’єднайте ці точки між собою відрізками. Назвіть відрізки, що перетинають пряму а і відрізки, що не перетинають її.
4. Поясніть, чому відрізки АВ і СD (із задачі 3) не перетинають пряму а, а останні – перетинають.
5. Пряма с перетинає відрізки РQ і QR. Чи перетинає вона відрізок PR. Відповідь пояснити.
6. Від променя АВ відклали два різних кути ВАС і ВАD однакової градусної міри. Чи перетинає пряму АВ відрізок СD?

Практична робота №4

Тема: Кут. Властивості  вимірювання кутів. Бісектриса кута.

Мета: навчитися будувати та вимірювати кути за допомогою транспортира; знаходити внутрішню та зовнішню області кутів; перевірити властивості вимірювання кутів та властивість бісектриси кута.

Обладнання: лінійка, олівець, транспортир, 3 кольорові олівці.

Хід роботи.

Завдання І.

1. Проведіть пряму;
2. Позначте на ній будь-яку точку;
3. Чи є утворена фігура кутом?
4. Побудуйте (ab) =135º;
5. Проведіть між сторонами (ab) промінь р так, щоб один з утворених кутів був прямим;
6. За допомогою транспортира виміряйте другий кут, який утворився після побудови;
7. Знайдіть суму величин  (ар) і  (bр), порівняйте її з величиною (ab);
8. Запишіть результати порівняння.

Завдання ІІ.

К          М               В             А            С                                  N                                    Р Мал. 1

Які з точок належать внутрішній області кута, а які зовнішній області цього кута (мал. 1)?

1. За допомогою транспортира перевірте рівність кутів А і М; В і С; К і Р (мал. 2). Частини внутрішніх областей відповідно рівних кутів розфарбуйте відповідно однаковими кольорами (потрібно 3 кольорових олівці).

В   А                                К

С                                               Р                   М

Мал. 2

Завдання ІІІ

С     А                       В Мал. 3

Користуючись транспортиром, в АВС проведіть бісектриси кутів А і В. Через точку перетину бісектрис і вершину С проведіть пряму. Виміряйте утворені частини кута С. Запишіть результат.

 

Тренувальні вправи

1. Користуючись транспортиром, знайти градусні міри кутів, зображених на мал. 4 - 6. Визначте вид кожного кута.

 

 

 

 

          Мал. 4                                Мал. 5                                   Мал. 6

2. Побудуйте кути, градусна міра яких дорівнює: а) 83º; б) 157º.
3. Розгорнутий кут поділено на дві частини, градусні міри яких відносяться 3׃7. Знайти ці частини.

С  В D                            А F             Мал. 7

Дано САВ =DAF. Доведіть, що САD=ВАF (мал. 7)

5. Кут між бісектрисою кута і продовженням однієї з його сторін дорівнює 124º. Знайдіть даний кут.

А      D         В                            С Мал. 8

Дано: АВС=110º; АВD=35º (мал. 8). Знайти: DВС.

 

Практична робота №5

Тема: Суміжні і вертикальні кути.

Мета: навчитися будувати суміжні і вертикальні кути, знаходити їх на малюнках, застосовувати властивості цих кутів при виконанні завдань практичних робіт.

Приладдя: олівець, лінійка, транспортир.

Хід роботи.

Завдання І.              1 Мал. 1

Продовжіть одну сторону кута 1 за його вершину. Як називаються кут 1 і отриманий кут? (мал. 1)

Завдання ІІ. Чи є на мал. 2 суміжні кути?

 

                                                                   5                7

                                                                      6                8

1    2                          3      4                                                           9  10

а                                   б                          в                      г                         д

Мал. 2

Завдання ІІІ.

С                 В     А                         D Мал. 3	Проведіть прямі АВ і СD, точку їх перетину позначте 0буквою О. Запишіть пари отриманих вертикальних кутів (мал. 3).
В              М                     К      D               О                                Р   А           F                 С Мал. 4	На мал. 4 знайти кілька пар суміжних кутів та кілька пар вертикальних кутів. Запишіть їх.

2. Побудуйте прямий, гострий та тупий кути. Для кожного з побудованих кутів побудуйте вертикальний кут. Знайдіть їх градусні міри.

Тренувальні вправи.

1. Накресліть два нерівних суміжних кути так, щоб їх спільна сторона була вертикальною.
2. Накресліть за допомогою транспортира АОВ=120º. Побудуйте кут, суміжний з АОВ із спільною стороною АО. Обчисліть його градусну міру.

2           1                           3   Мал. 5

Три прямі перетинаються в одній точці (мал. 5). Знайдіть кут 1, якщо 2+3=150º.

4. Один з кутів, які утворюються при перетині двох прямих у 4 рази більший за інший. Знайдіть ці кути.

α     β                  О Мал. 6

Різниця суміжних кутів αβ=30º. Знайдіть ці кути (мал. 6).

6. Знайдіть суміжні кути, якщо їх градусні міри відносяться як 2׃5.

Приклад уроку з використанням практичної роботи

Тема: Суміжні і вертикальні кути, їх властивості.

Мета:

навчальна: сформувати в учнів поняття про суміжні і вертикальні кути, навчити знаходити їх на рисунках; вивчити властивості цих кутів та застосовувати їх при розв’язуванні геометричних задач та виконанні практичної роботи.

виховна: виховувати вміння працювати самостійно та в колективі  (в групі), розширити математичний словник (термінологічний, символічний).

розвиваюча: розвивати логічне мислення.

Тип уроку: урок закріплення нових знань, вмінь та навичок.

Хід уроку.

1. Організаційний момент. Підготовка креслярського приладдя.
2. Перевірка домашнього завдання (робота в парах).

b                                a                      1              2   4                3       Мал.1	№1 Дано: a∩b 1+3=50º Знайти: 1, 3. Розв’язання. Два кути, які утворилися в результаті перетину двох прямих, вертикальні або суміжні. Дані кути не можуть бути суміжними, оскільки їх сума дорівнює 50º, а сума суміжних кутів становить 180º. Отже, вони вертикальні, вони рівні. Тоді кожний із них буде по 25º. Відповідь: 25º.
1    2                    4     3   Мал. 2	№2 Дано: 2=4х1 Знайти: 1, 2. Розв’язання. 1 і 2 – суміжні. 1 + 2=180º (за властивістю суміжних кутів) 1+41=180º; 1=180º׃5; 1=36º, 2=144º. Відповідь: 36º, 144º.

3. Актуалізація опорних знань учнів (фронтальне опитування).
   • Які кути називаються суміжними? Їх властивості.
   • Чи можуть два суміжні кути бути: а) гострими; б) тупими; в) прямими?
   • Які кути називаються вертикальними? Їх властивості.
   • Розв’язування задач усного рахунку з коментуванням відповіді.
4. Мотивація навчальної діяльності учнів.
5. Повідомлення теми і мети уроку.
6. Розв’язування задач.

2                 1          3                      4             Мал. 3	№1 Дано: a∩b, 2+3+4=335º. Знайти: 1, 2, 3, 4. Розв’язання. Розглянемо 2, 3. Вони суміжні. 2+3=180º. 180º+4=335º. 4=335º-180º=155º. 2=4 (як вертикальні), 2=155º. 3=180º-155º=25º. 3=1 (як вертикальні), 25º. Відповідь: 25º, 155º.
1                3           2   Мал. 4	№2 Дано: 1=2, 1=40º. Знайти: 3. Розв’язання. За умовою 1=2, тому 2=40º. 1+2 і 3 – суміжні, 3=180º-80º=100º. Відповідь: 100º.
а    1                                  2                          4       3                                     b Мал. 5	№3 Дано: прямі a і b -перетинаються, 3 у 8 разів менший за 2. Знайти: 1.   Розв’язання.    Нехай 3=х, а 2=8×х 2+3=180º (як суміжні). 8х+х=180º х=20º 3=20º 1=3 (як вертикальні). 1=20º. Відповідь: 20º.

7. Практична робота.

Побудувати прямий, гострий та тупий кути. Для кожного з побудованих кутів побудувати вертикальний кут.

8. Підведення підсумків уроку. Бліц турнір (робота в групах).

Бліц турнір

1. Чи можуть кути 120º і 50º бути суміжними?
2. Чи можуть кути 125º і 55º бути суміжними?
3. Чи можуть кути 181º і 1ºбути суміжними?
4. Чи можуть кути 90º і 90º бути суміжними?
5. Чи при вальне твердження: «Якщо один із суміжних кутів збільшити в два рази, то другий кут зменшиться у два рази»?
6. Що можна сказати про кожний з вертикальних кутів, якщо:
   • Їх сума більша за 180º;
   • Їх сума дорівнює 180º;
   • Їх сума менша 180º?

9. Оцінювання учнів.
10. Домашнє завдання (три рівні складності).

Практична робота №6

Тема: Перпендикулярні та паралельні прямі.

Мета: навчитися будувати та розрізняти на малюнках перпендикулярні та паралельні прямі.

Обладнання: таблиці «Паралельні прямі»; «Перпендикулярні прямі», лінійка, олівець, кутник креслярський, транспортир.

Хід роботи.

Завдання І.

С     A                             О                        B        D Мал. 1

Один з кутів, утворених при перетині двох прямих, прямий (мал. 1). Чому дорівнює решта кутів? AOC - ? СОВ - ? AOD - ? BOD - ? Як називаються прямі АВ та CD?

Завдання ІІ.

В                  D     А       С М          Е                                        Р    К Мал. 2

Розгляньте мал. 2. Чи перетинаються прямі АВ і CD; КЕ і МР? Як називаються прямі КЕ і МР?

Завдання ІІІ.

М   А                                              В Мал. 3

За допомогою креслярського кутника (мал. 3) через точку М проведіть пряму:  перпендикулярну до прямої АВ;  паралельну прямій АВ.

                                                                               а

 

                                     а

                                                                             А                           В

 

А                                      В

                                                                          

Завдання IV.

Визначити, які з прямих на мал. 4: а) паралельні; б) перетинаються; в) перпендикулярні. При необхідності використайте кутник та лінійку.                а      b                         m    n                                                                 a                                                                                         u                    c                                                                   v                      d                                                                      с      d     e         b                                                                                         Мал. 4

 

Тренувальні вправи.

1.     А                 а                                  b Мал.. 5	На мал. 5 дано дві прямі а та b, що перетинаються і точка А, що не належить цим прямим. За допомогою лінійки та кутника побудуйте прямі, що паралельні прямим а та b, та проходять через точку А.
2.                  ?      90°                       ?   Мал. 6	Два рівні тупі кути мають одну спільну сторону, а дві інші сторони взаємно – перпендикулярні. Знайти величини цих кутів (мал. 6).
3.              С                    3        4                2   A                  O        B Мал. 7	На мал. 7: 1=2; 3=4. Довести, що АВ⊥ОС.
4.                      В       А   Мал. 8	Через точки А і В проведіть прямі АС⊥а, BD⊥а (мал.8). Чому прямі АC і BD не перетинаються?
5.      D´                     C´     A´                      B´                D                   C   A                         B Мал. 9	Дано зображення куба (мал. 9). Знайти паралельні відрізки у квадратах, які є гранями куба.
6. Побудувати довільний ∆FST. За допомогою косинця та лінійки через вершину S провести  пряму, паралельну FT.

Практична робота №7

Тема: Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих.

Мета: навчитися знаходити внутрішні різносторонні, внутрішні односторонні, відповідні кути, утворені при перетині двох прямих січною; застосовувати ознаку паралельності прямих на практиці.

Приладдя: кутник, олівець, лінійка.

Хід роботи.

Завдання І.

с                        1   2 а                   4   3                   5   6 b            8  7 Мал. 1	Пряма с перетинає прямі а і b (мал. 1). Запишіть пари кутів, які утворилися при перетині прямих а і b. Внутрішні односторонні кути ____________ Внутрішні різносторонні кути____________ Відповідні кути ____________________ Як називається пряма с?
.           Мал. 2	Завдання ІІ. Подивіться вздовж даних ліній, вони здаються паралельними (мал. 2). Спостерігаєте зверху – прямі збігаються або розходяться. Оцінюючи розміщення прямих «на око», можна помилитися. Паралельність прямих потрібно доводити.
k                                      3                            1 4           m                            2                                             n Мал 3	Завдання ІІІ. Побудуйте дві прямі m і n та їх січну k так, щоб 1=2 (мал. 3). Доведіть: 1) 3=2; 2). 2+4=180º.

Доведення. (Вставте слова,яких не вистачає). 1 і 2 – це ___________ кути. За умовою 1=2, тому m і n  - ___________. 1) 3=2, як _____________. 2) 2+4=180º, тому що 2 і 4 – це _______________.

Якщо внутрішні різносторонні кути рівні то: 1) _______________ кути рівні; 2) сума _______________ кутів дорівнює 180º.

 

Тренувальні вправи

р                  1                          m                 2                        3                                               n Мал. 4	Дано: 1+3=180º (мал. 4). Довести: m||n.
а                               х       b        70º   Мал. 5	Яким має бути кут х, щоб а і b були паралельними (мал. 5)?

3. Один з кутів, що утворився при перетині двох паралельних прямих січною, дорівнює 68º. Знайдіть інші сім кутів.

В                                С                              О А                                    D Мал. 6	Дано: ВО=ОD; АО=ОС (мал. 6) Довести: АВ||СD.
В                            С     А                             D Мал. 7	Дано: АВ=СD; ВС=АD (мал. 7). Довести: АВ||СD і ВС||АD. Вказівка: проведіть діагональ і доведіть рівність трикутників.
А                   В                  С   Е                            D Мал. 8	Дано: (мал. 8) АВ||DЕ; ВАС=130º; СDЕ=60º. Знайти: кут АСD.

Практична робота №8

Тема: Трикутник і його елементи. Види трикутників.

Мета: навчитися будувати та знаходити на малюнках гострокутні, прямокутні, тупокутні трикутники та їх елементи.

Приладдя: кутник, лінійка, циркуль, кольорові олівці, транспортир.

Хід роботи.

Завдання І

В     А                                        С Мал. 1	Знайти на малюнку 1 основні елементи трикутника: Вершини (позначте їх кольоровим олівцем); Сторони (підпишіть їх на малюнку); Кути (позначте їх дугами і запишіть символами).
В             А                           С Мал. 2	Завдання ІІ В АВС зробіть побудови (мал. 2): Проведіть перпендикуляр ВD вершини В до прямої АС; Знайдіть середину К сторони АС і з’єднайте точку К з вершиною В; Проведіть пряму, що ділить кут В навпіл, до перетину її зі стороною АС в точці О. запишіть назви відрізків: ВD - ________; ВК - ____________; ВО - ____________.
А                                    С     мал. 3	Завдання ІІІ За допомогою креслярського трикутника проведіть перпендикуляр до відрізка АС  через точку С (мал. 3). На цьому перпендикулярі відкладіть відрізок СВ=3 см. Проведіть відрізок АВ. Трикутник АВС називається прямокутним. Сторони АС і СВ, що утворюють прямий кут, називаються катетами, сторона АВ називається гіпотенузою (підпишіть їх на отриманому малюнку).
В                   D     A                                C Мал. 4	В прямокутному трикутнику АВС проведіть CD﬩АВ за допомогою креслярського трикутника (мал.4). а) Між точками В і D позначте точку М і проведіть відрізок СМ. За допомогою транспортира виміряйте всі кути СМА. Запишіть результати: АМС=______; МСА=________; МАС=_________.

Трикутник АМС називається гострокутним: у ньому всі кути гострі.

b) На відрізку AD виберіть довільну точку К і проведіть відрізок КС. Виміряйте кути АКС. Запишіть результати: АКС=_______; КСА=_______; КАС=________. Трикутник АКС називається тупокутним: він має один тупий кут. Який?

Тренувальні вправи

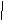1. Серед зображених на малюнках трикутників знайдіть гострокутні, тупокутні і прямокутні (мал. 5).

 

 

 

 

 

                                                                                                        

Мал. 5

2. Скільки трикутників на кожному малюнку (мал. 6)?

                    В                                              N

 

 

 

 

A           D                      C            M           F         K              P

                                                                         

Мал. 6

В         А                                С                Е                       D Мал. 7		Перерахуйте всі трикутники, дві вершини яких знаходяться в точках А і В (мал. 7).
В                  А                              С Мал. 8	В АВС проведіть всі три медіани за допомогою лінійки з поділками (мал. 8).
5.     В                                                    В1       А                          С    А1              С1 Мал. 9			За допомогою кутника й лінійки проведіть відрізок BD﬩СА. Відрізок BD називається висотою АВС. В А1В1С1проведіть висоту з вершини В1 (мал. 9).
6.              В                                            В1           А                             С    А1                 С1 Мал. 10			В АВС за допомогою лінійки і кутника проведіть висоту з вершини А й підпишіть її «висота». В А1В1С1 проведіть дві висоти. Скільки висот можна провести в трикутнику? Чи перетинаються вони в одній точці? (мал. 10).

 

Практична робота №9

Тема: Існування трикутника, що дорівнює даному.

Мета: навчитися будувати трикутник рівний даному.

Обладнання: лінійка, олівець, картон, ножиці.

Хід роботи.

1.               Зобразіть на картоні який-небудь трикутник, виріжте його.
2.               Накладіть на папір вирізаний трикутник і обведіть його, позначте вершини цього трикутника буквами А, В, С; ті ж самі букви поставте у відповідних кутах картонного трикутника.
3.               На тому самому аркуші паперу проведіть промінь MN .
4.               Розмістіть картонний трикутник так, щоб вершина А збігалася з точкою М, вершина В лежала на промені MN, а вершина С була у верхній півплощині відносно прямої MN.
5.               Обведіть картонний трикутник. Вершини трикутника, намальованого на папері, які відповідають вершинам трикутника АВС, позначте М, Р і Q.

∆АВС=∆MPQ.

Тренувальні вправи.

В     А                                  С Мал. 1

Побудуйте такий трикутник, у якого одна сторона співпадала б зі стороною ВС даного трикутника (мал. 1), інша сторона дорівнювала б стороні АС, але не співпадала б з нею, а третя – дорівнювала б стороні АВ.

2) ∆ABC=∆MKP, BC=6 м, С=26°, В=92°. Які кути і яку сторону ∆МКР можна визначити за цими даними?

3) ∆SKT=∆EAK, АК=8 см, S=20°. Яка із сторін ∆SKT дорівнює 8 см, а який з кутів ∆EAK дорівнює 20°?

4) Трикутники АВС і PQR рівні. Відомо, що АВ=3 дм, ВС=4 дм, PR=6 дм. Знайти невідомі сторони цих трикутників.

5) Трикутники з вершинами F, S, K і F, S,T рівні і мають спільну сторону FS, точки К і Т розташовані по різні сторони від прямої FS; FK=ST. Виконати схематичну побудову та записати рівність трикутників.

6) А                             С              В           D Мал. 2

На мал. 2 зображено рівні трикутники з відповідними рівними елементами. Запишіть рівність даних трикутників.

 

Практична робота №10

Тема: Ознаки рівності трикутників.

Мета: навчитися знаходити рівні трикутники на малюнках, доводити рівність цих трикутників, застосовуючи ознаки рівності трикутників.

Приладдя: олівець, лінійка, циркуль, транспортир.

Хід роботи.

Завдання І. Перша ознака рівності трикутників: за двома сторонами і кутом між ними.

1) B                          P                                F     A                                 C        M Мал. 1

На малюнку 1 трикутники рівні. За допомогою вимірювань знайти відповідно рівні сторони й відповідно рівні кути. Результати: A=____;B=____; C=_______.

AB=________;BC=_______; CA=________.

M=_____; K=______ ; P=________.

MK=________; KP=________; PM=_________.

Відповідно рівні сторони: ____________________________

Відповідно рівні кути: ___________________________

2)                                      В С1                                 А                                                             С               В1 Мал. 2	На двох прямих (мал. 2), що перетинаються побудували відрізки АВ1=АВ і АС1=АС. Чому ΔАВС=ΔАВ1С1? Поясніть.
3)                               С        А                                     В Мал. 3	Побудуйте трикутник, що дорівнює даному ΔАВС, продовжуючи сторони кута В (мал. 3).

Завдання ІІ. Друга ознака рівності трикутників: за стороною і двома прилеглими до неї кутами.

А                 D                         В          О                 С Мал. 4	На мал. 4 прямі OD∩AC=B. Відомо, що АВ=ВС і А=С. Доведіть, що ABD=СВО.
В       А                                     С Мал. 5	Накресліть А1В1С1 рівний АВС, використовуючи тільки транспортир і лінійку (мал. 5)
В   А                                  D                                          С Мал. 6	Відомо, що АD – бісектриса ВАС і ВС﬩АD. Доведіть, що АВD=АDС. Які з відрізків будуть рівними, якщо АВD=АDС (мал. 6). Запишіть ______________________

Завдання ІІІ. Третя ознака рівності трикутників за трьома сторонами.

1)                 В     А                          С     А1                  М Мал. 7

На прямій А1М відкладіть відрізок А1С1=АС (мал. 7). Розхилом циркуля рівним АВ з точки А1 проведіть дугу вище прямої А1М. Із точки С1 опишіть дугу, радіусом рівним СВ.

Точку перетину дуг позначте буквою В₁. Отримали трикутник А₁В₁С₁, сторони якого відповідно рівні сторонам ∆АВС. Позначте це на малюнку. Чи будуть ці трикутники рівними?

 

 

2)                              В   А                                     С Мал. 8

Нижче сторони АС ∆АВС (мал. 8) побудуйте ∆АСВ1, у якому: АВ1=АВ;  СВ1=СВ. З’єднайте точки В1 і В. Знайдіть рівні відрізки та рівні кути на отриманому малюнку. АВВ1=АВ1В (Чому?) __________________

СВВ₁=СВ₁В (Чому?) ______________________________________

АВС=АВ₁С (Чому?) ______________________________________

∆АВС=∆АВ₁С (Чому?)_______________________________________

 

 

Тренувальні вправи

1. На малюнку знайти рівні трикутники. В кожному випадку вказати ознаку, за якою трикутники рівні.

В                         1 2                    D     А                                   С Мал. .1 Дано: 1=2, BD – бісектриса кута АВС.

В                           С                                    1                    2 А                                D Мал. 2 Дано: ВС=АD, 1=2.

В                                О А                                            С Мал. 3 Дано: АВ=АС, СО=ВО.

2. На кожному із цих малюнків знайдіть рівні трикутники. В кожному випадку вкажіть ознаку, за якою трикутники рівні.

В                                             С А      D Мал. 4 Дано: АС ділить навпіл кути ВАD і BCD.

В               А              D              С Мал. 5 Дано: АВ=ВС, ВD – медіана сторони АС.

В     А   1     К                         С   2           D Мал. 6 Дано: АВ=АD, 1=2.

3. На кожному з цих креслень знайдіть рівні трикутники.

О             В           К                С         А                            D Мал. 7 Дано: К – середина ВС і середина АО.	D                         В                                 1                   К           2          А                             С Мал. 8 Дано: 1=2, К – середина АВ.		В                             С   А                                    D Мал. 9 Дано: АВ=ВD=DА, СА=СВ=СD.
4.                            С                   F                      Е         А                                          В Мал. 10		Дано: ∆АВС. Точка F лежить на стороні АС, точка Е лежить на стороні ВС, АЕ=ВF, АF=ВЕ. Довести, що ∆АВС -= рівнобедрений (мал. 10).
5.                      В                               В1                                  А1   А                             С                          С1 Мал. 11		Відомо, що АВ=А1В1, A=А1. В=В1. Проведіть бісектриси кутів А і А1 і доведіть, що ці бісектриси рівні (мал. 11).
6.                  В                            Е                         D     А                                    С Мал. 12		Дано: ∆АВС; BD=DC; DE=AD; AE  - пряма. Знайти рівні трикутники та довести їх рівність (мал. 12).

Практична робота №11

Мета: Рівнобедрений трикутник, його ознаки та властивості.

Мета: навчитися будувати рівнобедрений трикутник та його елементи, використовуючи ознаки та властивості рівнобедреного трикутника.

Приладдя: олівець, лінійка, циркуль.

Хід роботи.

Завдання І. Побудова рівнобедреного трикутника.

А                         В Мал. 1

Помістіть ніжку циркуля в точку А й проведіть дугу по одну сторону від відрізка АВ.

2.               Помістіть ніжку циркуля в точку В й таким самим розхилом циркуля проведіть дугу по ту ж сторону від АВ.
3.               Точку перетину дуг позначте буквою С. Проведіть відрізки АС і ВС.

В АВС сторони АС й ВС – рівні. Такий трикутник називається рівнобедреним; рівні сторони називаються бічними, третя  - основою.

Завдання ІІ.                            В                       1  2        А                D               С Мал. 2	Відомо, що в АВС АВ=ВС, 1=2. Уявно перегніть трикутник по прямій BD. Доведіть, що BDC суміщається з ABD. Пряма ВС співпадає з прямою АВ, тому що кут _________. Точка С співпадає з точкою А, тому що __________.
Завдання ІІІ.               В                                         В1   А                        С А1                С1 Мал. 3	Переконайтеся, що АВС і А1В1С1 – рівнобедрені. Не користуючись кутником, проведіть висоту А1В1С1 з вершини В1. Не користуючись транспортиром, проведіть бісектрису кута АВС.
Завдання IV.                                        В     А                                              С                                            D Мал. 4	АВС повернули навколо сторони АС, отримали ACD (мал. 4). Знайдіть на малюнку відповідно рівні відрізки. З’єднайте точки В і D. Знайдіть на малюнку рівнобедрені трикутники, запишіть їх назви. Знайдіть відповідно рівні кути. Запишіть їх.

 

Тренувальні вправи

В                     С     А                                             D                  Р                      К Мал. 5

В даному шестикутнику (мал. 5) проведіть всі діагоналі. Знайдіть спочатку рівносторонні, потім рівнобедрені (але не рівносторонні) і різносторонні трикутники, вершини яких є вершинами даного шестикутника.             Рівносторонні трикутники:___________             Рівнобедрені трикутники ____________             Різносторонні трикутники __________.

2. Заповніть таблицю малюнками трикутників:

		Гострокутні	Прямокутні	Тупокутні
Різносторонні
Рівнобедрені	Нерів- носторонні
	Рівносторонні

3. Знайдіть кути рівнобедреного  трикутника, якщо один з його кутів дорівнює 40º.
4.  Периметр рівнобедреного трикутника 3,4 м, а бічна сторона 1,3 м. знайти основу цього трикутника.

В                М                 Р      Т Мал. 6

В рівнобедреному ВМР (ВР=ВМ) зовнішній кут ВРТ рівний 126º. Знайти ВМР (мал. 6)

6. Доведіть, що якщо медіана трикутника є його бісектрисою, то він – рівнобедрений.

Практична робота №12

Тема: Ознаки рівності прямокутних трикутників.

Мета: навчитися застосовувати ознаки рівності прямокутних трикутників на практиці.

Приладдя: лінійка, олівець, циркуль, транспортир.

Хід уроку.

Завдання І. Ознаки рівності прямокутних трикутників: за двома катетами та за катетом і прилеглим до нього гострим кутом.

В       А                                          С Мал. 1	∆АВС – прямокутний (мал. 1); АСВ=90°. Продовжіть вправо катет АС і відкладіть СА1=СА. Продовжіть катет ВС вниз і відкладіть СВ1=СВ. Точки А1 і В1 з’єднайте. Доведіть, ∆АВС=∆А1В1С1.
М1 М                   О                    К                                                К1 Мал. 2	На прямій MК з обох сторін від точки О відкладіть відрізки ОА=ОВ (мал. 2). Через точки А і В проведіть за допомогою лінійки і кутника прямі, перпендикулярні прямій МК, до перетину з прямою М1К1. Доведіть рівність отриманих трикутників.

Завдання ІІ. Ознаки рівності прямокутних трикутників за гіпотенузою і гострим кутом та за гіпотенузою і катетом.

В                А                            С Мал. 3	∆АВС – прямокутний (мал. 3). На окремому аркуші паперу за допомогою транспортира побудуйте кут, що дорівнює куту А і від вершини побудованого кута відкладіть відрізок, рівний відрізку АВ. Із отриманої точки опустіть перпендикуляр на іншу сторону кута. Отриманий трикутник спробуйте сумістити з ∆АВС. Зробіть висновок: _______________________.
С        А                       О             В                                    D Мал. 4	Побудуйте взаємно-перпендикулярні прямі АВ і CD  OC=OA, CB=AD (мал. 4). Доведіть, що:                  ∆ВОC=∆AOD; OBD=ODB.

 

 

Тренувальні вправи

В                                   С        А                                      D Мал. 5	Дано: BAD=CDA=90°; AB=CD. Довести : AC=BD (мал. 5).
В                                С                               1                  2     A                                  D Мал. 6	Дано: B=D=90°; 1=2 Довести: AB=CD (мал. 6)
В             А             О        С                              D Мал. 7	Дано: AC﬩BD AO=OC; BO=OD. Довести: AB=BC=CD=AD (мал. 7).
А                                  В               1                                  2     D                                     С Мал. 8	Дано:AB﬩AD, CD﬩BC; AB=CD. Довести: 1=2 (мал. 8)
С        А            О               В                       D Мал. 9	Дано: АВ﬩СD; ОС=ОD; С=D. Довести: АС=ВD (мал. 9).
В                                 С    1                   К               М                        2         А                                   D Мал. 10	Дано: АВ=СD; ВМ﬩АС; DК﬩АС; ВМ=КD. Довести: АМ=СК; 1=2 (мал. 10).

 

Практична робота №13

Тема: Сума кутів трикутника.

Мета: переконатися, що сума кутів трикутника дорівнює 180º.

Обладнання: олівець, лінійка.

Хід роботи.

Завдання І.

D                  В                 К                  1´    2       3´   A      1                    3    C Мал. 1	Виріжте з паперу 2 однакові трикутники. Один з них приклейте справа у зошиті. Відріжте 2 кути від другого трикутника і приклейте їх так, як показано на мал. 1.
Отримаємо: BD || АС,  тому що …                       BK || AC, тому що … Промені BD і BK утворюють одну пряму, тому що 1´+2+3´=180º. Зробіть висновок про суму внутрішніх кутів  трикутника: 1+2+3= _____________________________________________________________.

 

Тренувальні вправи.

1. За даними мал. 2 обчислити невідомі кути АВС.

                А                                А                          В                          С

                                                                             125º                                   130°

 

      70º            60º                          80º           110º

С                           В     С                 В                                 

                               В                                                            А

 

 

             100º                                                  

40º   А                  С                                         

Мал. 2

2.  Кути трикутника відносяться як 1׃2׃3. Знайти кути даного трикутника.
3. У MNK: К=50º; N=100º. Знайти К.
4. Кут  при основі рівнобедреного трикутника дорівнює 72º. Знайти кут при вершині.

S        P                              T Мал. 3	Дано: SPT, ∠P – прямий. Довести: S - гострий, T – гострий. (мал. 3)
В           30º А             D            С Мал. 4	Дано: АВС; ВD – медіана; А =30º. Знайти інші кути АВС (мал. 4)

 

Практична робота №14

Тема: Зовнішній кут трикутника та його властивості.

Мета: навчитися розрізняти зовнішні та внутрішні кути трикутника на малюнках; знайти суму зовнішніх кутів трикутника, взятих по одному при кожній його вершині; перевірити властивість зовнішнього кута трикутника.

Приладдя: транспортир, лінійка, олівець.

Хід уроку.

Завдання І. Виміряйте за допомогою транспортира зовнішній кут ВСD трикутника АВС (мал. 1). Потім виміряйте внутрішні кути АВС не суміжні з кутом ВCD. Запишіть результати: BCD=_________; A=_______; B=_________. Порівняйте величини цих кутів й результати порівнянь запишіть за допомогою знаків >, <, =.

В       А          С                            D Мал. 1	а) BCD i A; б) BCD i B; в) BCD i A+B. Який висновок можна зробити?
Завдання ІІ.                     2         1                                                       3 Мал. 2	Визначте суму зовнішніх кутів трикутника, взятих по одному при кожній його вершині (мал. 2): 1+2+3=__________
Завдання ІІІ        М       А                 К                   С Мал. 3	Визначте, чому дорівнює сума внутрішнього кута трикутника МKCта його зовнішнього кута при вершині К (мал. 3): AKM=_________; MKC=_________; AKM+MKC=_________.

 

Завдання IV. На якому з малюнків кут 1 є зовнішнім кутом PKT (мал. 4)?

                К                                      К                        Р

         1

 

                                                                                               1

Р                           Т          1    Р                       Т                          Т                К

                                                                                                

Мал. 4

Тренувальні вправи

1. Як можна тільки за допомогою лінійки побудувати суму кутів А і В трикутника АВС?

В         М                                      Р        Т Мал. 5

У рівнобедреному ВРМ (ВР=ВМ) зовнішній кут ВРТ дорівнює 126º (мал. 5). Знайти кут РМВ.

3. Один із зовнішніх кутів рівнобедреного трикутника дорівнює 70º. Знайти кути цього трикутника. Скільки розв’язків має задача?
4. Знайти кути трикутника, знаючи, що зовнішні кути при двох його  вершинах дорівнюють 110º і 138º.
5. Один із зовнішніх кутів трикутника дорівнює 120º, а внутрішні кути, не суміжні з ним, відносяться як 5׃7. Знайти кути трикутника.
6. Знайдіть зовнішні кути прямокутного трикутника, якщо один з його гострих кутів дорівнює 65º.

Практична робота №15

Тема: Співвідношення між сторонами і кутами трикутника.

Мета: переконатися, що у трикутника: 1) проти більшої сторони лежить більший кут; 2) проти більшого кута лежить більша сторона.

Приладдя: транспортир, лінійка, олівець.

Хід роботи.

Завдання І.         В       А                                      С Мал. 1

За допомогою транспортира виміряйте кути АВС (мал. 1): А=________; В=________; С=_________.

За допомогою лінійки виміряйте довжини сторін АВС:

АВ=_______ ; ВС=_________; АС=________.

Результати вимірювань кутів і сторін запишіть в таблицю в порядку зростання довжин сторін.

1
2
3

Який висновок можна зробити з цієї таблиці про сторони, що лежать проти більших кутів і сторони, що лежать проти менших кутів?

Завдання IІ.         N                 M                                      K Мал. 2	За допомогою транспортира знайдіть в трикутнику ANK рівні кути. Виміряйте сторони, які лежать проти рівних кутів. Зробіть висновок про сторони, які лежать в трикутнику проти рівних кутів. Запишіть його.
Завдання IІІ.                                           B                 c                               a   A                      b                      C Мал. 3	В АВС (мал. 3) А=30º; В=60º; С=90º. Кут В вдвічі більший за кут А. Перевірте, чи вірно, що b=2a. Кут С втричі більший за кут А. Перевірте, чи c=3a.

 

Тренувальні вправи

А       С                                    В Мал. 4

У АВС АС<АВ. Порівняйте кути В і С цього трикутника (мал. 4) В АВС А>В. Порівняйте сторони ВС і АС (мал. 4)

 

Практична робота №16

Мета: Коло і круг. Взаємне розміщення двох кіл.

Мета: закріпити навички учнів будувати коло, заданого радіусу; проводити дотичну до кола в заданій на ньому точці. Розглянути взаємне розміщення двох кіл.

Приладдя: циркуль, лінійка, олівець.

Хід роботи.

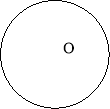
Завдання І. Точки А і В – кінці діаметра кола. За допомогою циркуля накресліть це коло. Позначте буквою О його центр. Виміряйте радіус та діаметр побудованого кола. Запишіть r =__________; d =________________.

Порівняйте радіус і діаметр кола. У скільки разів діаметр кола довший за його радіус?

Завдання ІІ.

В                                         С               А                                          D Мал. 1	Проведіть відрізки АС і BD. Точку їх перетину позначте буквою О. Із точки О опустіть перпендикуляр ОМ на АВ. Із точки О проведіть кола радіусами ОВ і ОМ. Запишіть назви відрізків, які є радіусами, хордами, діаметрами більшого кола.
Радіуси __________; Хорди ____________; Діаметри ____________. Завдання ІІІ.
А                        С                                  В Мал. 2		Через дані точки кола провести дотичні до кола. Як називаються точки А, В, С (мал.1)?
М       Мал. 3		Через точку М до кожного з кіл проведіть дотичні (мал.2).
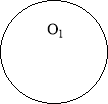
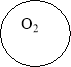
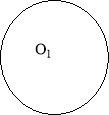
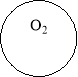
Завдання ІV.                                                        О                           О                   а)                                     б) Мал. 4		Радіуси двох кіл ОО1 і ОО2. Знайдіть відстань між їх центрами, якщо кола мають: а) внутрішній дотик; б) зовнішній дотик.

 

Тренувальні вправи

1. Накресліть коло, радіус якого дорівнює 2,5 см. Проведіть у ньому радіус, діаметр і хорду.
2. Дано пряму а і точку А на ній. Побудуйте коло радіусом 3 см, що дотикається до прямої а у точці А.

N             K                  M мал. 1	На мал. 1 КОМ=46º, точка О – центр кола. Знайдіть KMN.
В                            А   Мал. 2	Два кола мають спільний центр О. Їх радіуси відносяться як 9׃5, а АВ=8 см. визначте радіуси кіл.

5. Два кола з центрами у точках А і В мають спільну точку дотику К, радіуси даних кіл дорівнюють 4 см і 2 см. Знайдіть АВ.
6. Чайнворд.

Частина кола між двома точками, які лежать на колі.             Великий вчений Стародавньої Греції, який запровадив формулу для обчислення довжини кола.             Відрізок, що сполучає дві точки кола і проходить через його центр.             Відрізок, який сполучає центр кола з довільною точкою кола.

5.          Частина круга, обмежена двома радіусами і дугою кола, що з’єднує їх кінці.
6.          Скорочене позначення  радіанної міри кута.

Практична робота №17

Тема: Побудова відрізка, що дорівнює даному. Поділ даного відрізка навпіл.

Мета: навчитися будувати відрізок, що дорівнює даному відрізку; навчитися будувати середину даного відрізка.

Приладдя: олівець, лінійка, циркуль.

Хід роботи.

Завдання І. Побудова відрізка, що дорівнює даному.

1) Зобразіть відрізок АВ та промінь з початком  точці К (мал. 1).

2) Побудуйте циркулем коло з центром у точці К та радіусом АВ (мал. 2). Це коло перетне промінь у деякій точці D. Очевидно, що KD=AB. Тому KD  - шуканий відрізок.

Замість кола можна було провести деяку його частину (дугу), яка б напевне перетинала промінь (мал. 3).

 

А          В

                                                            D                                           D

                                               К                                            К

 

К

        Мал. 1                              Мал. 2                                        Мал.3

Завдання ІІ. Поділ даного відрізка навпіл.

М     (2)        А                Р         В                         N Мал. 4

Із точки А розхилом циркуля, більшим за половину відрізка АВ, опишіть дугу (1) (мал. 1) Із точки В таким самим розхилом циркулям опишіть дугу (2) до перетину з дугою (1) в точках М і N. МN перетинає АВ в точці Р. Р – шукана точка. Р – середина АВ.

Доведення. AMN=BMN (за трьома сторонами). Тому АМР=ВМР. МР– бісектриса рівнобедреного трикутника АМВ з основою АВ, тому вона є також медіаною. Отже, Р – середина АВ.

Тренувальні вправи

C                             D Мал. 5	Проведіть довільний промінь та відкладіть від його початку відрізок, що дорівнює даному відрізку СD (мал. 5).
А                     В Мал. 6	Побудуйте пряму с, виберіть на ній точку О і опишіть коло з центром у точці О і радіусом, що дорівнює відрізку АВ (мал. 6). У скількох точках коло перетнуло пряму?
М                                      N Мал. 7	Поділити відрізок MN навпіл (мал. 7).
В   А                                  С Мал. 8	У АВС провести медіану до більшої сторони.

5. Накресліть довільний відрізок. Побудуйте відрізок, що дорівнює ¾ накресленого відрізка.
6. Накресліть довільний відрізок РТ та коло з центром у точці Р, радіус якого дорівнює РТ.

Практична робота №18

Тема: Побудова кута, що дорівнює даному. Побудова бісектриси кута.

Мета: навчитися відкладати від даного променя кут, що дорівнює даному куту та будувати бісектрису даного кута.

Приладдя: циркуль, лінійка, олівець, транспортир.

Хід роботи.

Завдання І. Побудувати кут, що дорівнює даному куту А так, щоб одна з його сторін збігалася з променем, початок якого у точці О.

1) Візьмемо на сторонах кута А довільні точки В і С (мал. 1).

2) Побудуємо трикутник ОКМ, що дорівнює трикутнику АВС, так, щоб АВ=ОК, АС=ОМ, ВС=КМ (мал. 2).

В                            К         А                                     О                           М            Мал. 1                             Мал. 2

3) Тоді КОМ=ВАС. 4) Отже, КОМ – шуканий. Доведення. ОКМ=АВС (за побудовою), а тому КОМ=А.

Завдання ІІ. Побудова бісектриси даного кута.

Нехай задано кут А, необхідно побудувати його бісектрису (мал. 3).

В             (2)  D                                 (3)     А                      С мал.  3

Проведемо дугу кола довільного радіуса з центром у точці А (дуга (1) на мал. 3), яка перетинає сторони кута в точках В і С.             Із точок В і С опишемо дуги такими самими радіусами (дуги (2) і (3)) до їх перетину всередині кута (точка D). Промінь АD- шукана бісектриса кута А.

Доведення. АВD=ACD (за трьома сторонами), а тому BAD=CAD, отже AD – бісектриса кута А.

Тренувальні вправи

Р                       К                            О Мал. 4

Побудуйте кут, що дорівнює даному (мал. 4).

2. Побудуйте за допомогою транспортира кут, що дорівнює 125º, та без транспортира побудуйте його бісектрису.
3. Побудуйте АВС, якщо АВ=4 см, АС=6 см, С=110º.
4. Побудуйте АВС за стороною АВ=4 см і кутом: А=40º і В=60º.
5. Побудуйте прямий кут; кут 45º; кут 22,5º; кут 135º.
6. Побудуйте EFS за стороною EF, бісектрисою ЕК і кутом F.

Практична робота №19

Тема: Побудова трикутника за трьома сторонами.

Мета: навчитися будувати трикутник за трьома його сторонами.

Приладдя: циркуль, лінійка, олівець.

Хід роботи.

Завдання І. Побудувати трикутник за трьома сторонами.

А              а                               (4)          (3)              b                              с                      b             с                        (1)                                  (2)                                      р   В             а               С                                Мал. 1

Нехай задано три відрізки а, b і c (мал. 1).              За допомогою лінійки проведемо довільну пряму р і позначимо на ній довільну точку В (1);

2. За допомогою циркуля відкладемо на прямій р відрізок ВС=а (дуга (2));
3. Розхилом циркуля, що дорівнює b, опишемо дугу (3) кола з центром у точці С;
4. Розхилом циркуля, що дорівнює с, опишемо дугу (4) кола з центром у точці В;
5. Точка А – точка перетину дуг (3) і (4). Трикутник АВС – шуканий.

Доведення. ∆АВС – шуканий, оскільки сторони ∆АВС дорівнюють заданим відрізкам а, b і c: ВС=а; АС=b; АВ=с.

Зауваження: Задача має розв’язок тільки якщо сума довжин 2-х даних відрізків більша довжини третього.

 

Тренувальні вправи

1. Побудувати ∆АВС, якщо АВ=5 см, АС=3 см, ВС=4 см.
2. Побудувати трикутник за двома сторонами і кутом між ними, якщо АВ=5см, АС=6 см, А=40°.
3. Побудувати трикутник за стороною і прилеглими до неї кутами:  АВ=6 см, А=30°,В=50°.
4. Побудуйте рівнобедрений трикутник за бічною стороною і кутом при основі.
5. Побудуйте трикутник за двома сторонами і медіаною, проведеною до однієї з них.
6. Побудуйте трикутник за двома сторонами і медіаною, проведеною до третьої сторони.

Практична робота №20

Тема: Побудова прямої, перпендикулярної до даної прямої.

Мета: навчитися будувати пряму, перпендикулярну до даної прямої.

Приладдя: циркуль, олівець, лінійка.

Хід роботи.

Завдання І.Через дану точку М провести пряму, перпендикулярну до даної прямої а, якщо:

І випадок. Точка М належить прямій а:                                 В                     (3)          (2)                                                   (1) а            К              М                L Мал. 1

Побудова. На даній прямій а довільним розхилом циркуля відкладемо від точки М два рівних відрізки МK=ML (дуги (1) мал. 1); Із центрів K і L розхилом циркуля, що дорівнює КL, опишемо дуги (2) і (3) до їх перетину в точці В;

3. Пряма ВМ перпендикулярна до прямої а.

Доведення. ВМ – медіана рівностороннього трикутника ВКL, тому вона є також висотою. Отже, ВМ﬩а.

ІІ випадок. Точка М не належить прямій а:                                М                                        (1) а            В                           С                          (2)                                  N   Мал. 2

Побудова.                  З точки М довільним радіусом (більшим за відстань від точки М до прямої а) проведемо дугу (1), яка перетинає пряму а в точках В і С (мал.2);               Із центрів В і С цим самим розхилом циркулем опишемо дуги (2) і (3) до їх перетину в точці N (відмінної від точки М)

3. Пряма MN перпендикулярна до прямої а.

Доведення. Нехай точка F – точка перетину прямих ВС і MN. ∆BMN=∆CMMN (за трьома сторонами). Тому BNMN=CMN. MF – бісектриса рівнобедреного трикутника BMC, проведена до його основи. Тому MF є також висотою. Отже, MF﬩DC, а тому MN﬩a.

 

Тренувальні вправи

1. Накресліть пряму а та точку К, що не належить цій прямій. Проведіть пряму КМ, перпендикулярну до а.
2. Через точку Е, яка лежить на прямій m, провести пряму k перпендикулярну до даної прямої m.
3. Дано трикутник. Побудуйте його висоту.
4. Побудуйте коло, описане навколо даного трикутника.
5. Побудуйте рівнобедрений трикутник за основою та висотою, проведеною до основи.
6. Побудуйте трикутник за стороною, кутом, прилеглим до неї та висотою, проведеною до даної сторони.

РОЗДІЛ ІІІ

ПЕРЕВІР СВОЇ ЗНАННЯ

 

Тема: Основні властивості найпростіших геометричних фігур.

Кросворд І

1               2                 3                     4                 5

Частина прямої, яка складається з усіх точок цієї прямої, що лежать по один бік від даної на ній точки.                  Частина прямої, яка складається з усіх точок цієї прямої, що лежить між двома даними її точками.

3.                  Наука, яка вивчає властивості геометричних фігур.
4.                  Твердження, яке містить формулювання основних властивостей найпростіших фігур і не потребує доведення.
5.                  Основна геометрична фігура, яку прийнято позначати великими літерами латинського алфавіту.

Кросворд ІІ

1                 2                   3               4       5

Твердження, яке доводять. Слово, яке в перекладі з грецької мови на українську означає «землемірство». Назва праці з геометрії, автором якої був давньогрецький учений Евклід.

4. Геометрична фігура, яка складається з точки та двох різних променів, які виходять із цієї точки.
5. Твердження про властивості найпростіших фігур, яке не потребує доведення.

Тема: «Кути»

Кросворд ІІІ

1   2   3       4                                     5                 6                     7                     8             9                                               10

По горизонталі: Промінь, який виходить з вершини кута, проходить між його сторонами і ділить його навпіл. 5. Кут, вершина якого лежить на колі, а сторони перетинають це коло. 6. Кут, який більший за прямий, але менший від розгорнутого. 7. Кут, суміжний з кутом трикутника при певній вершині. 9. Кути, сторони яких є доповняльними пів прямими до сторін іншого. 10. Фігура, яка складається з двох пів прямих, що виходять з однієї точки.

По вертикалі:

1. Кут, що дорівнює половині розгорнутого кута. 2. Пряма розбиває площину на дві … 3. Кут, який менший від прямого. 8. Одиниця вимірювання кутів.

 

Тема: «Трикутники»

Кросворд ІV

1                         2             3             4                         5                   6                   7                       8                 9

Один із видів трикутників. Один із видів кутів. Перпендикуляр, проведений з вершини трикутника до прямої, що містить протилежну сторону. Лінія, яка поділяє кут навпіл. Сума яких кутів трикутника дорівнює 180º?

6. Найбільша сторона у прямокутному трикутнику.
7. Градусна міра якого кута дорівнює сумі градусних мір двох внутрішніх кутів трикутника, не суміжних з ним?
8. Катет, протилежний куту 30º, дорівнює … гіпотенузи.
9. Сторони, що утворюють прямий кут трикутника.

Якщо ти правильно розгадав кросворд, то у виділених клітинках отримаєш назву геометричної фігури, яка найчастіше використовується в задачах.

Тема: «Геометричні побудови»

Кросворд V

1   2   3               4         5                                             6               7                                                     8

По горизонталі: 3. Відрізок , що сполучає дві точки кола. 5. Розміщення двох прямих. 6. Найбільша хорда. 8. Коло, яке дотикається до всіх сторін трикутника. По вертикалі: 1. Геометрична фігура. 2. Відрізок, що сполучає центр кола з будь-якою точкою на колі. 4. Відрізок, який сполучає вершину трикутника з серединою протилежної сторони. 6. Пряма, що проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. 7. Коло, яке проходить через всі вершини чотирикутника.

 

Відповіді до кросвордів:

Чайнворд (ст. 60) Дуга. Архімед. Діаметр. Радіус. Сектор. Рад. Кросворд І. Промінь. Відрізок. Геометрія. Аксіома. Точка. Кросворд ІІ. Теорема. Геометрія. Начала. Кут. Аксіома. Кросворд ІІІ. По горизонталі: Бісектриса. Вписаний. Тупий. Зовнішній. 9.Вертикальні. 10. Кут.

По вертикалі: Прямий. Півплощини. Гострий. 8.Градус. Кросворд IV. Гострокутний. Прямий. Висота. Бісектриса. Внутрішніх. Гіпотенуза. Зовнішнього. Половині. Катети. Кросворд V. По горизонталі: 3.Хорда. 5.Перпендикулярні. 6.Діаметр. 8.Вписане. По вертикалі: Трикутник. Радіус. 4.Медіана. 6.Дотична. 7.Описане.

 

ВИСНОВКИ

 

1. Практичні роботи розвивають в учнів конструктивний підхід до осмислення всього комплексу знань з геометрії (планіметрії);
2. Виконання практичних робіт сприяє правильному розумінню учнями геомерії як науки про властивості просторових форм, грунтовному засвоєнню програмного матеріалу з геометрії виробленню умінь практично застосовувати його, розвитку логічного мислення, просторової уяви.
3. Застосування практичних робіт інтенсифікує навчально-виховний процес, підвищує коефіцієнт корисності навчального часу; посилює сприйняття того матеріалу, який в інших умовах подання є складним або навіть недоступним розумінню деяких учнів. Всі учні класу включаються в роботу, пасивних немає. Весь урок триває кропітка пізнавальна праця.
4. Практичні роботи сприяют розвитку механічного та смислового запам'ятовування, якості мислення (глибина, ширина, самостійність). Мислення учнів стає творчим, гнучким.
5. Для практичних робіт характерна значна творча складова. Їх виконання пробуджує цікавість до навчального матеріалу.

ЛІТЕРАТУРА

 

1. Істер О.С. Геометрія-7. Підручник для 7 кл. загальоосвіт. навч. закл.-К.:Освіта,2007.-159 с.
2. Лоповок Л.М. Збірник задач з геометрії для 6-8 класів. Посібник для вчителів.-К.:Радянська школа,1983.-104 с.
3. Бурда М.І. Розвязування задач на побудову в 6-8 класах. Метод. Посібник.-К.:Рад.шк.,1986.-112 с.
4. Істер О.С. Усні вправи з алгебри та геометрії. 7 клас.-Тернопіль:Підручники і посібники,2001.-64 с.
5. Мерзляк А.Г., Полонський В.Б., Рабінович Ю.М., Якір М.С. Збірник задач і завдань для тематичного оцінювання з геометрії для 7 класу.-Х.6Гімназія,2007.-112 с.
6. Погорєлов О.В. Геометрія: Планіметрія. Підручник для 7-9 класів загальноосвітніх навчальних закладів.-К.:Школяр,2004.-240 с.
7. Генденштейн Л.Е., Єршова А.Г.. Наочний довідник з геометрії дл 7-11 класів.-Харків.-Гімназія,1997.-96 с.