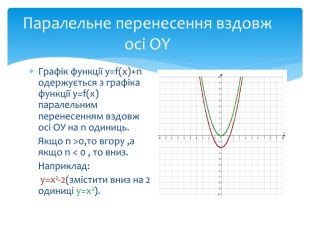
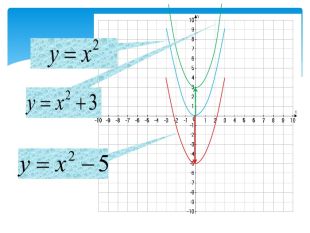
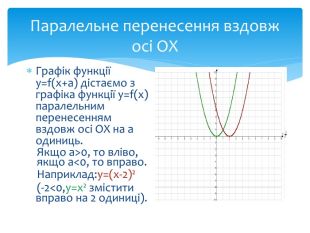
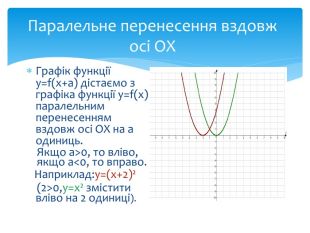
Найпростіші перетворення графіків функцій
Про матеріал
Алгебра, 9 клас. Розробка уроку у вигляді презентації на тему: "Найпростіші перетворення графіків функцій", яка включає в себе пропедевтичну практику, презентацію нового матеріалу, закріплення вивченого та його повторення. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
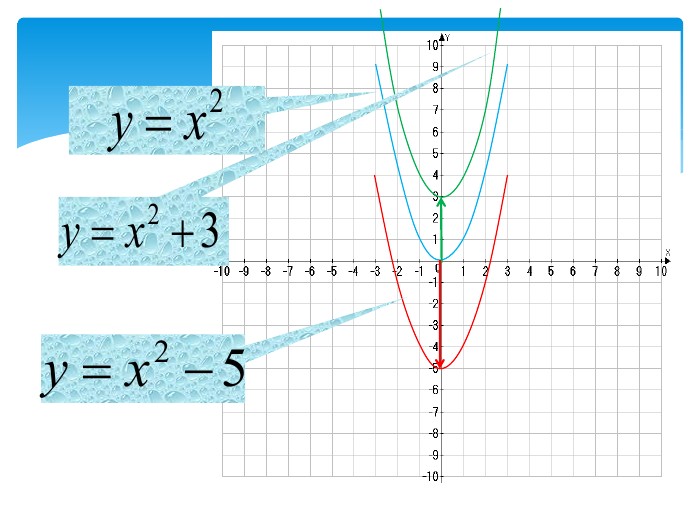
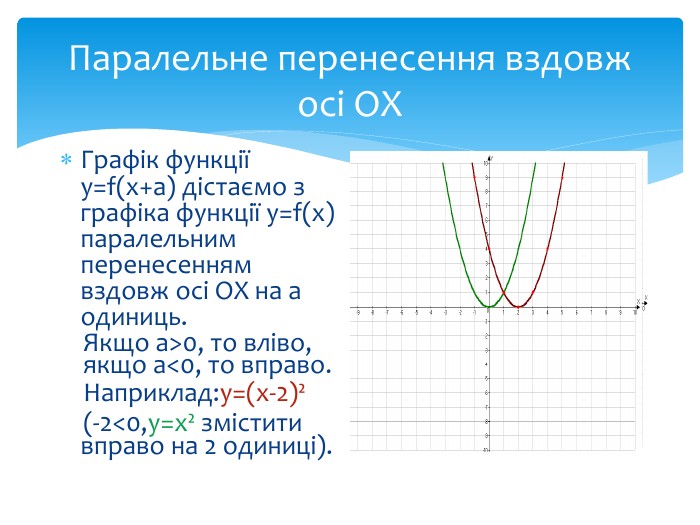
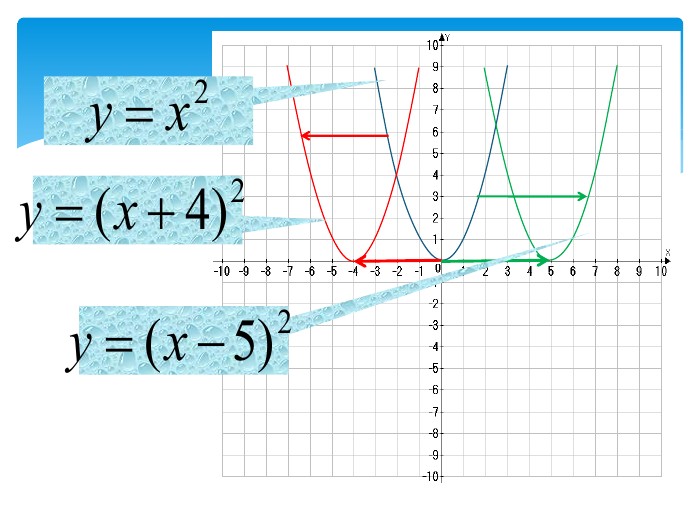
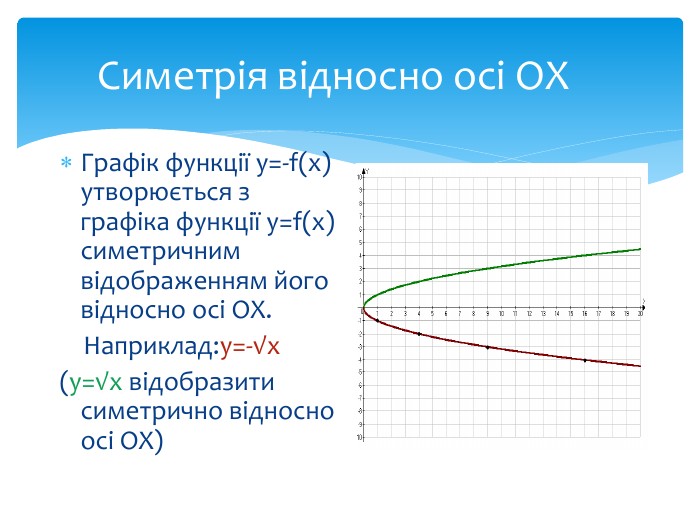
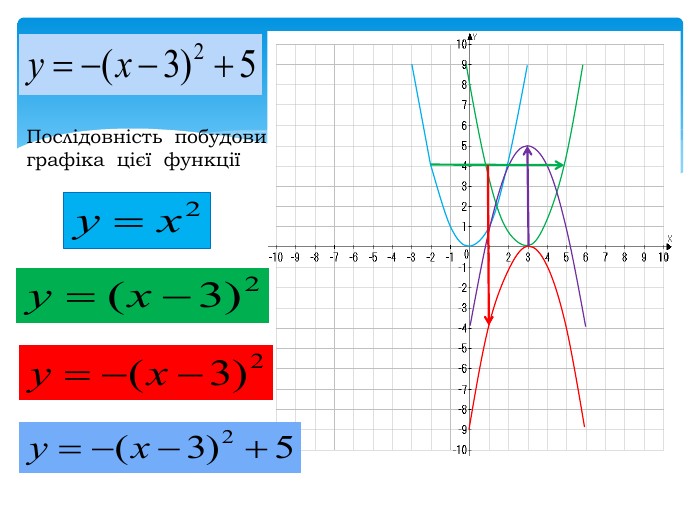
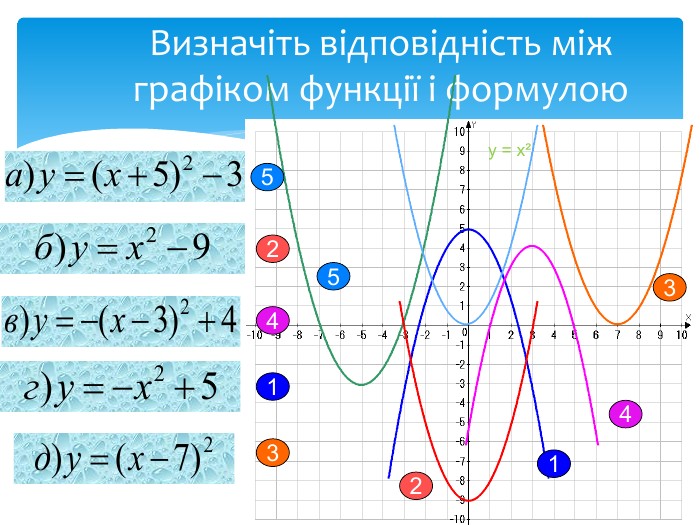
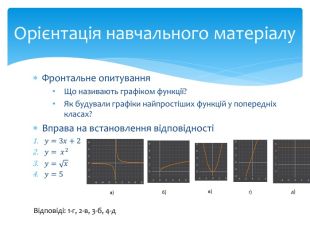
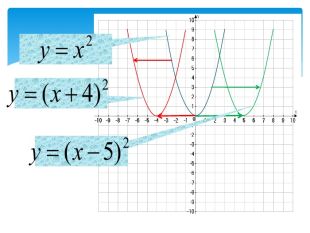
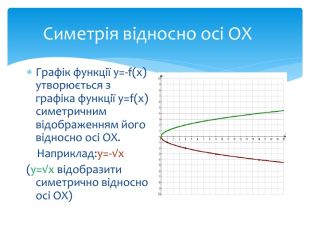
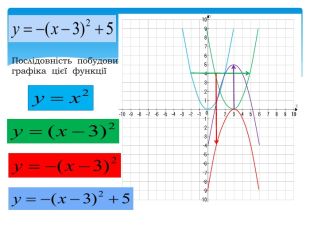
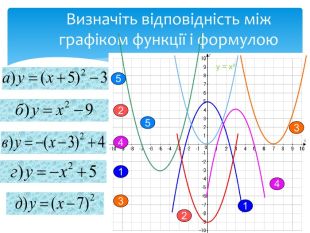
10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x) Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку