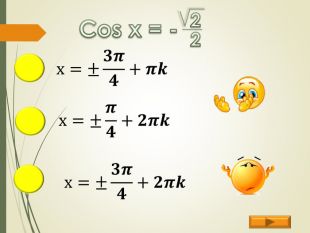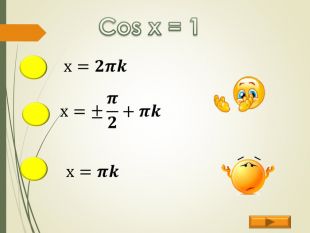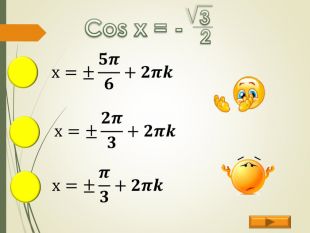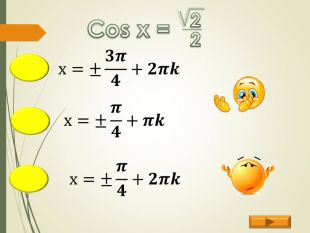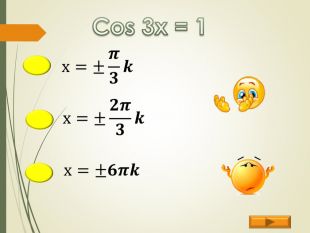Найпростіші тригонометричні рівняння (презентація)
Про матеріал
Матеріали до вивчення теми з алгебри "Тригонометричні функції", до уроку вивчення найпростіших тригонометричних рівнянь. До цього уроку ще додається матеріали для учня та викладач Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку









![6. Що називається арккосинусом числа a?Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а. 6. Що називається арккосинусом числа a?Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а.](/uploads/files/86568/209635/225715_images/9.jpg)