Урок. Деякі способи розв`язування тригонометричних рівнянь.
Методична розробка уроку
Клас 10
Предмет Алгебра
Тема уроку Деякі способи розв’язування тригонометричних рівнянь
Мета уроку Формування в учнів умінь розв’язувати тригонометричні рівняння
способом:
- заміни змінних;
- зведення до однієї тригонометричної функції з однаковим аргументом;
- розкладанням на множники;
- введення допоміжного кута;
- зведення до однорідного рівняння.
Розвивати логічне мислення, уяву, пам'ять, виховувати інтерес до математики, уважність, відповідальність, культуру математичних записів, позитивне ставлення до навчання.
Хід уроку
І Організаційна частина
Ми навчилися розв’язувати найпростіші тригонометричні рівняння sin x = a, cosx = a, tgx= a, ctgx = a.
Сьогодні на уроці ми будемо розв’язувати складніші тригонометричні рівняння і познайомимось з деякими способами розв’язування тригонометричних рівнянь.
Слайд 1
ІІ Повідомлення теми уроку
Тема: «Деякі способи розв’язування тригонометричних рівнянь».
Слайд 2
Епіграфом до сьогоднішнього заняття я взяла слова великого математика Р.Декарта.

Тригонометричні рівняння дуже складні, тому класифікуємо їх, запишемо алгоритми розв’язань деяких рівнянь і будемо їх застосовувати.
ІІІ Основна частина
1) Заміна змінних при розв’язуванні тригонометричних рівнянь
Сьогодні ми навчимось розв’язувати складніші тригонометричні рівняння, які шляхом поточних перетворень можна звести до рівнянь з однією тригонометричною функцією, потім зробити заміну і звести до алгебраїчного рівняння.
Слайд 3
Приклад 1. Розв’язати рівняння
2 sin2x + sinx – 1 = 0
В ході пояснення задаю питання учням, спонукаю до спільного обговорення розв’язку, учні записують розв’язання у зошит.
Розв’язання.
Введемо нову змінну t = sin x.
Оскільки sin x – функція обмежена, то t ϵ [-1;1]
Тоді дане рівняння буде мати вигляд ![]() .
.
Розв’яжемо його: ![]() ,
, ![]() ,
, ![]() .
.
Тому, ![]() або
або ![]() .
.
Слайд 4
1) ![]() ,
,
![]() ,
,
![]() .
.
2) ![]() ,
,
![]() .
.
Відповідь: ![]() ,
, ![]() .
.
2) Розв’язування тригонометричних рівнянь зведенням до однієї функції (з однаковим аргументом).
Слайд 5
Приклад 2. Розв’язати рівняння
6sin2x + 5cosx – 2 = 0
Обговорюється хід розв’язування рівняння, проектується розв’язання, записують у зошит.
Замінимо ![]() на
на ![]() і отримаємо квадратне рівняння відносно
і отримаємо квадратне рівняння відносно ![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Нехай ![]() ,
, ![]() , тоді
, тоді ![]() ,
, ![]() ,
, ![]() - сторонній корінь. Отже,
- сторонній корінь. Отже, ![]() ,
,
![]() ,
, ![]() .
.
Відповідь: ![]() ,
, ![]() .
.
Слайд 6
Алгоритм розв’язування рівнянь зведенням до однієї функції (з однаковим аргументом).
- Спробувати всі тригонометричні функції звести до одного аргументу.
- Якщо вдалося звести до одного аргументу, то спробувати всі тригонометричні вирази звести до однієї функції.
- Зробити заміну.
- Звести рівняння до квадратного.
- Розв’язати квадратне рівняння.
- Повернутись до заміни і розв’язати утворені рівняння.
- Записати відповідь.
Слайд 7
Приклад 3. Розв’язати рівняння ![]()
Чи можна це рівняння записати відносно однієї тригонометричної функції? Виконайте це.
Чи можна це рівняння записати у вигляді квадратного рівняння відносно однієї змінної?
Розв’яжіть рівняння, перевірте правильність виконання, виправте помилки.
Розв’язання. Оскільки ![]() то рівняння можна записати у вигляді
то рівняння можна записати у вигляді
![]() .
.
Позначимо ![]() . Отримаємо рівняння
. Отримаємо рівняння ![]() , яке зводиться до квадратного
, яке зводиться до квадратного![]()
![]()
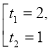
![]()
![]()
![]()
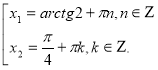
Відповідь: ![]() .
.
Слайд 8
3) Розв’язання тригонометричних рівнянь за допомогою розкладання на множники.
Приклад 4. Розв’язати рівняння ![]() .
.
Розв'язання. У лівій частині рівняння винесемо за дужки спільний множник і застосуємо формули подвійного кута: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Відповідь: ![]()
4) Однорідні тригонометричні рівняння.
Якщо всі члени рівняння у лівій і правій частинах якого стоять многочлени від двох змінних (або від двох функцій однієї змінної) мають однаковий сумарний степінь, то рівняння називається однорідним. Розв’язують однорідне рівняння діленням на найвищий степінь однієї змінної.
Зауваження. Дотримуючись цього орієнтира, доводиться ділити обидві частини рівняння на вираз зі змінною. При цьому можлива втрата коренів, якщо коренями є числа, при яких дільник дорівнює нулю. Щоб уникнути втрати коренів, необхідно окремо розглянути випадок, коли вираз, на який ми збираємось ділити обидві частини рівняння, дорівнював нулю, і лише після цього виконувати ділення на вираз що не дорівнює нулю.
Розглянемо рівняння виду ![]() (однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:
(однорідне рівняння 1-го степеня), де а і b не дорівнюють нулю. Значення х, при яких cos x дорівнює нулю, не задовольняє даному рівнянню, бо тоді і sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно на cos x. Маємо:![]() ,
, ![]()
![]() .
.
Розв’язавши дане тригонометричне рівняння отримуємо корені.
Рівняння виду
![]()
називається однорідним рівнянням 2-го степеня.
Якщо числа a, b, c не дорівнюють нулю, то розділимо дане рівняння на ![]() (або на
(або на ![]() ). (У даному рівнянні
). (У даному рівнянні ![]() , бо в супротивному випадку
, бо в супротивному випадку ![]() , а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
, а cos x і sin x не можуть одночасно дорівнювати нулю). Тоді
![]()
![]() .
.
Розв'язавши отримане, рівняння одержимо корені даного рівняння.
Приклад 5. Розв’язати на дошці, коментуючи кожен крок. Залучати студентів до обговорення.
![]()
ОДЗ: ![]()
![]() ділимо на
ділимо на ![]()
![]()
Заміна ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
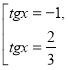
![]()
![]()
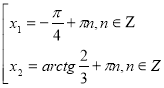
Відповідь: ![]()
5. Метод введення допоміжного кута.
Розглянемо рівняння виду asinx + bcosx = c. Очевидно, що ![]() .
.
Поділимо обидві частини рівняння на ![]() і покладемо
і покладемо ![]() та
та ![]() , маємо рівняння
, маємо рівняння ![]() , або
, або ![]() . Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови
. Отже, дістали просте тригонометричне рівняння яке має розв’язки за умови![]() .
.
Слайд 9
.
- Встановіть відповідність між рівнянням і методом розв’язання.
- Розв’яжіть рівняння.
|
Рівняння |
Методи |
|
1) |
А) Зведення до однорідного рівняння n-го степеня.
|
|
2) |
Б) Метод введення допоміжного кута. |
|
3) |
В) Заміна змінних |
|
4) |
Г) Метод розкладання на множники. |
|
5) |
Д) Метод зведення до однієї функції (з однаковим аргументом). |
|
6) |
Е) Заміна змінних |
|
7) |
|
|
8) |
|
|
9) |
|
Заключна частина:
- Узагальнення і систематизація, запам’ятання, закріплення знань.
- Підсумки заняття
- Повідомлення домашнього завдання
1


про публікацію авторської розробки
Додати розробку

-

Shevchuk Alla
14.02.2023 в 10:56
Дуже вдячна за розробку уроку
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Стецько Олександра Іванівна
09.02.2023 в 16:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горобець Ірина Вікторівна
24.03.2022 в 15:18
Щиро дякую!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Расторгуєва Олена
22.01.2022 в 23:10
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук