Тема: Неевклідова геометрія

Зміст

1.                        В чому суть геометрії Лобачевского?
2.                        Гаус. Його вклад в неевклідову геометрію.
3.                        Ріман та Больяі. Їхній вклад в неевклідову геометрію.
4.                        Застосування геометрії Лобачевского.

Геометрія в перекладі з грецького означає „землемірство”. Древньогрецький вчений Евдем Родоський (IVст. до н. е.) так писав про геометрію: „Геометрія була відкрита єгиптянами і виникла при вимірюванні Землі. Це вимірювання було їм необхідне внаслідок розливу річки Ніл, яка постійно змивала границі”. Слова Евдема Родоського пояснюють нам назву цієї науки, яка виникла із її практичної необхідності і направленості.

 Остаточне формування геометрії в самостійну науку відбулося в середині Vст. до н.е. і закінчилось створенням в IIIст. до н.е. „Начал” Евкліда.

„Начала” Евкліда  складалися з 13 книг і зіграли вирішальну роль в розвитку геометрії. Цей твір отримав загальне визнання чіткої, логічної системи математичних знань. До цього часу вивчення геометрії в школах всього світу ґрунтується на Евклідових началах.

Аж до XVII ст. математики вивчали і аналізували геніальну працю Евкліда, зокрема V постулат.

Сам Евклід формулював його так: ”Якщо пряма перетинає дві прямі і утворює внутрішні односторонні кути в сумі менші за дві прямі, то при нескінченному своєму продовженні вони перетнуться з цієї сторони, де сума двох кутів менша за дві прямі.” Інші формулювання набагато простіші, наприклад: „через точку поза прямою можна провести одну і тільки одну пряму паралельну даній.” Звичайно, ще сам Евклід намагався вивести цей складний постулат з більш простих. Після нього цією проблемою займалися майже всі відомі математики, але найчастіше все це закінчувалось тим, що постулат виводився тільки при накладанні додаткових умов. У менш вдалих математиків не виходило взагалі нічого.

Найвідомішою спробою довести п’ятий постулат методом від супротивного було здійснено італійським монахом Джироламо Саккерті в 1733р. та зусилля були марними.

Лише майже через 2000р. після Евкліда професор Казанського університету М.І. Лобачевский, припустивши, що можливо існує інша геометрія, де це твердження не виконується, розробив нову неевклідову геометрію, яка на той час не могла „вкластися” в головах учених.

В чому полягає геометрія Лобачевского?

 У геометрії Лобачевського зберігаються всі теореми, які в евклідовій геометрії можна довести без використання п’ятого постулату       ( або аксіоми паралельності, одного з еквівалентів п’ятого постулату ,яка включена нині у шкільну програму).

Наприклад, ”вертикальні кути рівні”, „ кути при основі рівнобедреного трикутника рівні”, „із даної точки можна провести на дану пряму тільки один перпендикуляр”. Зберігаються також ознаки рівності трикутників та ін. Проте теореми, під час доведення яких застосовується аксіома паралельності, видозмінюються.

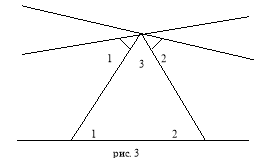
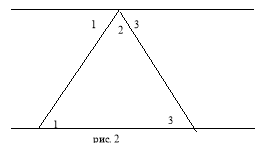
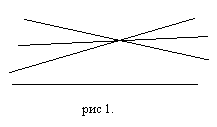Інколи говорять, що в геометрії Лобачевского паралельні прямі перетинаються в нескінченності, але це не зовсім так. Існує лише трішки інша властивість паралельності: через одну точку поза прямою можна провести нескінченно багато прямих паралельних даній. Це видно на рис 1.  Причому паралельність зберігається лише в сторону зменшення відстані між прямими. Цей здавалось би простий факт змінює всю геометрію. Наприклад, як в геометрії Евкліда доводилося, що сума кутів трикутника дорівнювала 180°? Класичне доведення зображено на рис. 2. Використовується властивість внутрішніх різносторонніх кутів при паралельних прямих і січній, тоді отримуємо, що 1+2+3=180^о. Оскільки в геометрії Лобачевського паралельність зберігається тільки в одному напрямі, то для знаходження суми кутів трикутника необхідно провести дві прямі, паралельні даній в різні сторони. Результат можна побачити на рис. 3. Зрозуміло, що тепер сума кутів трикутника менша 180°. Цю різницю Лобачевский назвав дефектом трикутника.

Одним з найважливіших об’єктів на площині Лобачевского є пучки прямих. Але щоб описати ці пучки , треба зрозуміти, що в площині Лобачевского є три типи розміщення прямих:

1. Паралельні прямі
2. Прямі, що перетинаються;
3. Прямі, що розходяться;

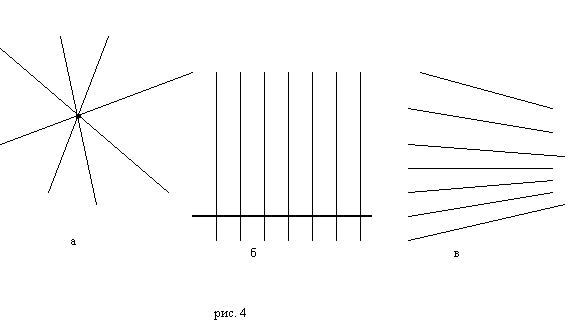
Оскільки перший тип пучків утворений прямими, які мають спільну точку – центр пучка (рис. 4а). Пучок прямих, які розходяться – це перпендикуляри до одної прямої – осі пучка (рис. 4б). З цього означення випливає цікаве, здавалось би на перший погляд абсурдне твердження, що два перпендикуляри до однієї прямої непаралельні, на відміну від геометрії Евкліда.

І, нарешті, пучок, утворений прямими паралельними даній в заданому напрямку (рис. 4в).

Наступними об’єктами геометрії Лобачевского є криві. Для їх побудови Лобачевским було введено поняття відповідних точок.

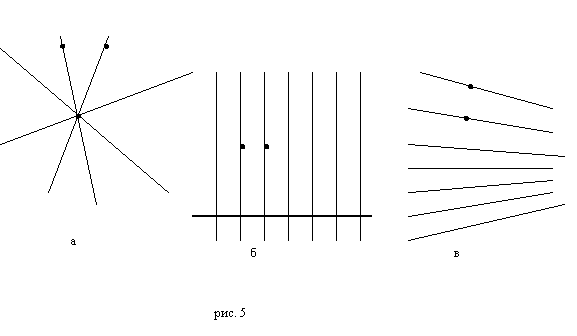
 В пучку першого роду ці точки на прямих, рівновіддалені від центру(рис. 5а)

.В пучку  другого роду ці точки прямих, лежать по одну сторону від осі і на однаковій віддалі ( рис. 5б).

В пучку третього роду вони розміщені симетрично бісектриси  смуги між двома прямими, на яких лежать ці точки (рис.5в.)

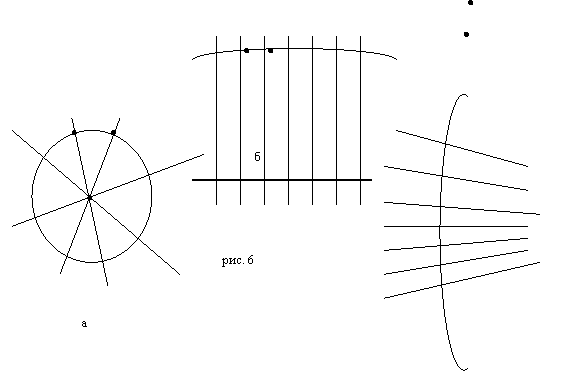
З’єднавши відповідні точки першого пучка, ми отримуємо коло. В випадку другого пучка ми отримуємо лінію рівних відстаней, а в третьому випадку – так звану граничну лінію. Приклади таких побудов зображені на рис.6.

Ідея неевклідової геометрії прийшла в голову не , тільки Лобачевскому, просто йому відносно повезло.

Одним із ”конкурентів” був німецький математик Гаус , який відмовився від послуг пошти, щоб ніхто не зміг його звинуватити в плагіаті.

Карл Фрідріх Гаус народився 30 квітня 1777 р. у Брауншвейгу – одному з німецьких князівств, які на той час ще не були об'єднані в єдину централізовану державу. Гаус цікавився  геометрією. Окремі питання, як, наприклад, найважливіша проблема геометрії – проблема V постулату Евкліда – привертали його особливу увагу. У своїх міркуваннях він ішов шляхами, схожими па ті, які проробив Лобачевський, але не опублікував жодної сторінки. У листі до математика Бесселя Гаус писав: «Певне, я ще не скоро зможу обробити свої широкі дослідження з цього приводу так, щоб їх можна було опублікувати. Можливо, навіть, що я не зважуся на це протягом усього мого життя, тому що боюсь крику беотійців, які піднімаються, коли я висловлюю свої погляди».

Гаус ознайомився з результатами досліджень Лобачевського за невеликою брошурою «Геометричні дослідження з теорії паралельних прямих», написаною німецькою мовою і виданою у 1840 р. Він зацікавився цією працею і в свої 62 роки вирішив вивчити російську мову, щоб мати можливість читати твори Лобачевського в оригіналі. У листах до своїх друзів Гаус з великою похвалою говорив про досягнення Лобачевського. Він писав, що праця Лобачевського містить основи тієї геометрії, яка могла б бути і була б цілком послідовною, якби геометрія Евкліда не була правильною. Він писав також, що вже 54 роки (з 1792 р.) має такі самі переконання. Самому Лобачевському Гаус власноручно написав листа, в якому повідомив російського вченого, що його обрали членом-кореспондентом Геттінгенського математичного вченого товариства.

. Дуже цікавими із спадщини вченого є його щоденник і дослідження з неевклідової геометрії й теорії еліптичних функцій. Зокрема, з опублікованих матеріалів видно, що Гаус прийшов до думки про можливість існування поряд з евклідовою геометрією неевклідової в 1818. Проте побоювання, що ідеї неевклідової геометрії не зрозуміють у математичному світі, і, можливо, недостатнє усвідомлення їх наукової важливості були причиною того, що Гаус їх далі не розробляв і нічого за життя з цих питань не опублікував. Коли опублікував неевклідову геометрію М.І. Лобачевський, Гаус поставився до цього з великою увагою і запропонував обрати Лобачевського членом-кореспондентом Геттінгенського вченого товариства, але власної оцінки Лобачевського по суті не дав.

В цей час син старого друга Гауса Янош Больяі  зайнявся теорією паралельних прямих. В 1832 році він випустив працю „Апендикс”, яка містила початки неевклідової геометрії. Але його робота майже співпала з мемуарам Лобачевского „Про початки геометрії” 1829 року; подібних результатів досягнув і сам Гаус.

Тоді Гаус написав Фар кашу Больяі те, що той сам говорив сину: ще не прийшов час для таких викладок. Януш вважав, що Гаус вирішив присвоїти собі його працю. Але Гаус не публікував цього – адже він був королем математики цього періоду, і боявся, що його вважатимуть безумцем.

Але якщо Януш Больяі вважав себе генієм – одиночкою, то Гаус взнав про Лобачевского, прочитав „Геометричні дослідження по теорії паралельних прямих Миколи Лобачевського”. Гаус казав, що читаючи цю працю, він бачить в першу чергу себе. Гаус почав вивчати російську мову. Але – іронія долі – Гаус встидався відкрито попросити працю Лобачевского, а той не відсилав її в Геттінген, бо не знав, що Гаус розуміє російську.

Через шість років Гаус все ще думає про Лобачевского. Він розуміє, що вже занадто старий, щоб захищати нові ідеї. А Лобачевский гинув без підтримки. Больяі ж, отримавши в 1848 році „Геометричні дослідження”, подумав, що Гаус випустив мемуар під псевдонімом Лобачевский. Ціллю його життя було перевершити цю працю. Це була агонія розуму – а Лобачевский навіть не підозрював про існування талановитого угорця.

За рік до цього, зимою 1848 року, до гауса прийшов студент. Його звали Бернард Ріман. Але Гаус відштовхнув його. Тоді Ріман, стиснувши зуби, поїхав в Берлін. Але світ тісний, і, захистивши докторську дисертацію, він вирішує стати професором. Дивно, але тему пробної лекції приймає саме Гаус.

Ріман створив геометрію, де прямі замкнуті, де нема паралельних прямих, а сума кутів трикутника більша 180^о. Вона подібна на геометрію сфери Гауса.

Ріман виявився хорошим учнем великого математика, і з небажаного гостя став єдиним другом. Він помер в Італії, не закінчив останній мемуари. Російською мовою він появився тільки в 1893 році. Він називався „Про гіпотези, які лежать в основі геометрії”.

Гаус, Больяі, Ріман, Швейкарт, Таурінус - всі вони рано чи пізно переконувались, що довести п’ятий  постулат неможливо. Спроб було багато –але саме неможливість довести це твердження привело до відкриття неевклідової геометрії.

Застосування геометрії Лобачевского в математиці та фізиці.

Сам  Лобачевский  вказував на застосування неевклідової геометрії. По -перше, було важливо перевірити, чи не суперечать властивості реального простору його новій більш загальній геометрії.

Якщо врахувати, що  для нескінченно малих фігур , нова геометрія збігається з звичайною, то з того, що для земних відстаней завжди підтверджується досвідом правильність евклідової геометрії, ще не випливає, що на величезному просторі геометрія виявиться також евклідовою.

Лобачевский висловив припущення, що з розширенням можливостей точних спостережень, коли незрівнянно більші простори Всесвіту будуть доступні вивченню, може з’ясуватись, що в просторі діє його геометрія.

Другу галузь застосування своєї теорії він знайшов усередині самої математики. Багато інженерів, фізиків, математиків не знають, що в сучасних довідниках і таблицях визначених інтегралів містяться формули, отримані М.Лобачевським методом його уявної геометрії.

Розвиток фізики показав, що геометрія Лобачевского є необхідною складовою частиною теорії відносності. Одне з таких застосувань було знайдено російським фізиком О.Фрідманом.

У 1922році, спираючись на ідеї загальної теорії відносності і розв’язуючи рівняння Ейнштейна, він знайшов важливий вид лінійного елемента, з якого випливало, що Всесвіт розширюється з часом. Метрика Фрідмана при фіксованому часі виявилася простором Лобачевского, тому фізики називають нині цей чотиривимірний ріманів простір простором Фрідмана – Лобачевского.

М. Лобачевский не залишав до останніх днів життя своїх наукових досліджень, і його геніальні сміливі ідеї руйнували тисячолітні канони та визначали подальший розвиток математичних наук.

Література

1. І.Я. Галай, Г.Д. Гриневич. Учащимся  о выдающихся математиках.

     2 О.І. Бородін, А.С. Бугай. Біографічний словник діячів у галузі математики

     3 Широков П.А. Краткий очерк основ геометрии Лобачевского./. – М.: Наука, 1983.

     4 Колесников М. Лобачевский./. Серия «Жизнь замечательных людей». – М.: Молодая гвардия.

     5 Александров А.Д. О геометрії Лобачевского / Математика в школе.-№2.-1993