Нерівності. Теорія та практика
НЕРІВНОСТІ
|
Доведення нерівностей |
|
1.Довести нерівність: |
|
Доведення. Знайдемо різницю лівої та правої частин нерівності:
Сума додатних взаємно обернених чисел не менша за 2. |
|
Зауваження:рівність має місце при а = b. |
|
2.Довести нерівність: |
|
Доведення. Знайдемо різницю лівої та правої частин нерівності:
|
|
Зауваження:рівність має місце лише при а = bабо а = b = 0. |
|
Приклад. Доведемо нерівність |
|
Доведення. Подамо вираз |
|
Основні властивості числових нерівностей |
|
1.Якщо a > b, то b< a. |
|
Доведення |
|
a >b |
|
2.Якщо a<b, b<c, то a<c. |
|
Доведення |
|
a<b
(a–b)+(b–c) = a–b+ b–c= a–c<0 |
|
3.Якщо а<b, ас — будь-яке число, то а + с<b + с. |
|
Доведення |
|
a<b |
|
4.Якщо a<b, c>0, то aс <bс і
Якщо а<b, с<0, то ас>bc; |
|
Доведення |
|
a<b Отже, якщо а<bі с>0, то ас<bc; c<0, то ас>bс.
Нерівності |
|
Наслідки з властивостей числових нерівностей |
|
1.Якщо а<b + с, то а–с<b. |
|
Доведення
a<b + c |
|
2.Якщо а>0іb>0,іa<b,то |
|
Доведення
a<b
|
|
Приклад. Відомо, що а<b. Порівняємо значення виразів: 2а + 3і 2b+5. |
|
Розв'язання а<b | ∙2;оскільки 2>0, то 2а<2b|+3; 2а + 3<2b+3. 3<5|+2b; оскільки 2>0, то 2b + 3 < 2b+5.
Отже, |
|
Якщо точне значення величини х не відоме, але можна визначити, між якими числами а і Ь це значення міститься на числовій прямій (тобто a< х < Ь ), то кажуть, що значення величини оцінено х. |
|
Приклад. Відомо, що -1 <х <3. Оцінимо значення виразу 2x–5. |
|
Розв'язання |
|
Встановимо послідовність дій у виразі 2х–5: спочатку х помножимо на 2, а потім додамо до цього виразу -5: х |
|
Помножимо всі частини одержаної нерівності -1 <х <3 на 2 > 0, при цьому знак нерівності не зміниться: -2 <2х < 6. |
|
Додамо до всіх частин нерівності число -5, при цьому знак нерівності не зміниться: -7<2х–5<1. |
|
Теорема (властивість) про почленне додавання числових нерівностей |
||||||
|
Якщо а<bі c<d, то a + c<b+d. |
||||||
|
Доведення
|
||||||
|
Теорема (властивість) про почленне множення числових нерівностей |
||||||
|
Якщо 0<а<b і 0<c<d, то ac<bd. Доведення
Наслідок. Якщо 0<а<b, то an<bn, де п — натуральне число. |
||||||
|
Доведення |
||||||
|
|
(за теоремою про почленне множення числових нерівностей). |
|||||
|
Приклад 1. Відомо, що 3<а<4; 2 <b< 3. Оцінимо значення виразу:
1)а + b;2) а-b;3) аb;4) Розв'язання |
||||||
|
1) |
|
2)а- b = а+(-b) 2<b <3| ∙ (-1) - 2>-b>-3
|
3) |
|
4) (0<)2<b <3
|
|
|
Приклад 2. Доведемо нерівність (т + п)(тп + 1)>4тп, якщо т>0, п>0. |
||||||
|
Доведення
Використавши нерівність |
||||||
|
т + п ≥ 2
тп+1 ≥ 2 |
||||||
|
За теоремою про почленне множення нерівностей перемножимо нерівності (1) і (2) почленно. Тоді маємо:
(т + п)(тп + 1) ≥ 2 |
||||||
|
(т + п)(тп + 1) ≥ 4 (т + п)(тп + 1) ≥ 4тп, де m≥ 0, п ≥ 0. |
||||||
|
Нерівності з однією змінною та їхні системи і сукупності |
|
1.Нерівність з однією змінною Якщо двавиразизі змінноюпоєднатиодниміззнаків > (більше); < (менше); ≥ (більше або дорівнює); ≤ (менше або дорівнює), то отримаємо нерівність з однією змінною. |
|
Наприклад: х2 + 1>х–1;3х–1 ≥ x + 2;
Розв'язком нерівності зі змінною називається значення змінної, при якому дана нерівність перетворюється на правильну числову нерівність. Наприклад, для нерівності |
|
2.Система нерівностей з однією змінною Якщо треба знайти спільні розв'язки нерівностей з однією змінною, то кажуть, що треба розв'язати систему нерівностей. Систему нерівностей записують за допомогою фігурної дужки. |
|
Наприклад: |
|
Розв'язком системи нерівностей з однією змінною є значення змінної, яке є розв'язком кожної з нерівностей системи. |
|
Наприклад:х = 3є розв'язком системи 3 –3<1 і 2 ∙ 3 –1>3 є правильними нерівностями (х = 3є розв'язком кожної з нерівностей). |
|
3.Сукупність нерівностей з однією змінною Якщо ставиться завдання знайти значення змінної, яке є розв'язком хоча б однієї з даних нерівностей, то кажуть, що слід розв'язати сукупність нерівностей. Сукупність нерівностей записують за допомогою квадратної дужки. |
|
Наприклад: Розв'язком сукупності нерівностей з однією змінною називається таке значення змінної, яке є розв'язком хоча б однієї з нерівностей сукупності. |
|
Наприклад: х = 1є розв'язком сукупності є розв'язком нерівності 2х–1<3 (при х = 1ця нерівність перетворюється на правильну: 2 ∙ 1 –1< 3). |
|
Розв'язати нерівність (систему нерівностей або сукупність нерівностей) означає знайти всі її розв'язки або довести, що їх немає. |
|
|
Числовий проміжок — вид запису множин, що є розв'язками нерівностей з однією змінною. Види числових проміжків |
|
|
|
|
Проміжок |
Приклад |
|
|
|
1. а<х< b
|
2<x <3
|
|
|
|
2. а ≤ х ≤ b
|
2 ≤ х ≤ 3
|
|
|
|
3. х>а
|
х> -2
|
|
|
|
4. х ≥ а
|
х ≥ -2
|
|
|
|
5. х<а
|
х<3
|
|
|
|
6. х ≤ а
|
х ≤ 3
|
|
|
|
Переріз і об'єднання проміжків
Приклад 1. Розв'яжемосистему нерівностей
|
|
|
|
Розв'язання.(3;5)—спільна частина проміжків(3; + ∞) і (-∞; 5), тому (3;5) — це переріз проміжків (3; + ∞) і (-∞; 5)(розв'язок системи
Відповідь: (3; + ∞) |
|||
|
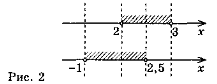
Приклад 2. Розв'яжемо систему нерівностей |
|||
|
|
|||
|
Розв'язання. Проміжок (-1;3) складається з чисел, які є розв'язком хоча б однієї з нерівностей 2 <х <3 або -1 <х <2,5, тому є об'єднанням цих проміжків (розв'язком сукупності).
Відповідь: (2; 3) |
|||
|
Дві нерівності називають рівносильними, якщо вони мають ті самі розв'язки. |
|
|
Деякі рівносильні перетворення нерівностей |
|
|
1.Якщо з однієї частини нерівності перенести в іншу частину доданки з протилежними знаками, то утвориться нерівність, рівносильна даній. Наприклад: 2x –3>6 і 2х>9 —рівносильні нерівності. |
|
|
2.Якщо обидві частини нерівності помножити (або поділити) на те саме додатне число, то утвориться нерівність, рівносильна даній.
Наприклад: 2x>6 і х>3, |
|
|
3.Якщо обидві частини нерівності помножити (поділити) на те саме від'ємне число і змінити знак нерівності на протилежний, то утвориться нерівність, рівносильна даній. |
|
|
Наприклад: -3х>6 і х<-2; |
|
|
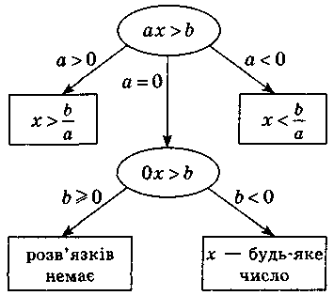
Лінійна нерівність з однією змінною— нерівність виду ах>b, або ах<b, або ах ≥ b, або ах ≤ b, де а,b— дані числа, ах — змінна. Наприклад: 3х>1; -x<-3; 0х>3; 0х<0 —лінійні нерівності. |
|
|
Схема розв'язування лінійної нерівності |
|
|
|
|
|
Приклад розв'язування нерівності, що зводиться до лінійної: |
|
|
Розв'язати нерівність 9(х–1)+5х<17х–11 |
Коментар |
|
9х–9+5х<17х–11 14х–9<17х–11 |
1. Виконаємо тотожні перетворення лівої(і правої) частин нерівності. |
|
14х–17х<-11 + 9 -3х< -2 |
2.Перенесемо відомі доданки в однучастину нерівності, а невідомі — в іншу. Тотожно перетворимо обидві частини. |
|
х >
x
Відповідь: |
3. Оскільки коефіцієнт при х у лівій частині утвореної нерівності не дорівнює нулю, поділимо на нього обидві частини нерівності, змінивши її знак на протилежний (бо -3<0). Запишемо відповідний числовий проміжок — це і є відповідь — розв'язок даної нерівності. |
|
Основні кроки розв'язування нерівностей з однією змінною |
|
|
1.Якщо нерівність містить дроби, то множимо обидві частини нерівності на найменший спільний знаменник усіх дробів, які входять у нерівність. |
|
|
2.Якщо в нерівності є дужки, то розкриваємо їх. |
|
|
3.Переносимо доданки зі змінною в одну частину нерівності, а інші доданки — у другу частину. |
|
|
4.Зводимо подібні доданки,одержуємо лінійну нерівність. Розв'язуємо лінійну нерівність за схемою (див.опорний конспект № 8). |
|
|
Приклад. Розв'яжемо нерівність: |
|
|
3(у + 1)+2у– 1 <6у; 3у + 3 + 2у–1<6у; |
5y+2<6y; 5у–6у<-2; -у<-2; у>2. |
|
Відповідь: y |
|
|
Основні кроки розв'язування системи нерівностей з однією змінною |
|
1. Розв'язуємо кожну нерівність системи. 2. Зображуємо множину розв'язків кожної нерівності на однійкоординатній прямій. 3. Знаходимо переріз числових проміжків, записуємо відповідь. |
|
Приклад. Розв'яжемо систему нерівностей Розв'язання
|
|
Основні кроки розв'язування сукупності нерівностей з однією змінною 1. Розв'язуємо кожну нерівність сукупності. 2. Зображуємо множину розв'язків кожної нерівності на однійкоординатній прямій. 3. Знаходимо об'єднання числових проміжків, записуємо відповідь. |
|
Приклад. Знайдемо розв'язок сукупності нерівностей |
|
Розв'язання
|
|
Відповідь: x |


про публікацію авторської розробки
Додати розробку

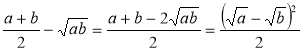 . Оскільки
. Оскільки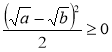 ,тобтонерівність
,тобтонерівність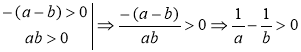 .
.
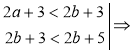 2а + 3<2b + 5.
2а + 3<2b + 5.
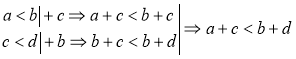 .
.
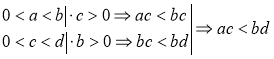 .
.
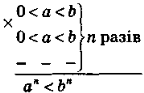
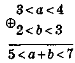
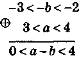

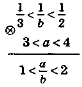
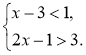
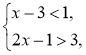 бо прих = 3
бо прих = 3
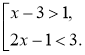
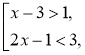 бо х = 1
бо х = 1
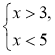 (рис. 1).
(рис. 1).

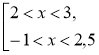 (рис. 2).
(рис. 2).
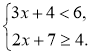
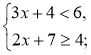
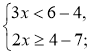
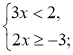
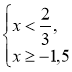 (див. рисунок).
(див. рисунок).  Відповідь: х
Відповідь: х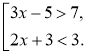
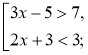
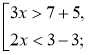
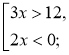
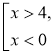 (див. рисунок).
(див. рисунок).