Об'єми та площі поверхонь геометричних тіл

 

МЕТА: повторити, систематизувати й узагальнити знання учнями:

• Формул для обчислення об’ємів паралелепіпеда, призми, піраміди, циліндра, конуса, кулі;
• Формул для обчислення площі бічної та повної поверхонь циліндра і конуса;
• Формули для обчислення площі сфери.

ТИП УРОКУ: узагальнення і систематизація знань, умінь і навичок.

ХІД УРОКУ

І. Організаційний етап

Перевірка готовності учнів до уроку, налаштування на роботу.

ІІ. Перевірка домашнього завдання.

Перевіряємо правильність виконання домашнього завдання за зразком з коментуванням:

1. Розв’язати рівняння: 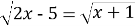. Відповідь: 6.
2. Спростити вираз: 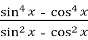. Відповідь: 1.
3. Знайти значення виразу: 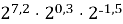. Відповідь: 64.
4. Розв’язати рівняння: 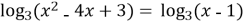. Відповідь: 4.
5. Знайти довжину вектора 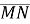, якщо M(2;3;-5), N(2;-6;7). Відповідь: .

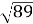ІІІ. Формулювання мети й завдань уроку.

Оскільки урок є останнім, підсумковим, то увага приділяється повторенню, узагальненню й систематизації знань і вмінь учнів, набутих під час вивчення теми.

IV. Повторення й систематизація знань.

Контрольні запитання:

1. Чому дорівнює об’єм прямокутного паралелепіпеда?
2. Як обчислити об’єм призми.
3. Як обчислити об’єм піраміди.
4. Чому дорівнює об’єм циліндра?
5. Як обчислити об’єм конуса.
6. Як обчислити об’єм кулі.
7. За якою формулою обчислюють площу бічної поверхні циліндра.
8. Як знайти площу повної поверхні циліндра?
9. За якою формулою обчислюють площу бічної поверхні конуса.
10. Як знайти площу повної поверхні конуса.
11. За якою формулою обчислюють площу сфери.

V. Повторення й систематизація вмінь.

Виконання усних вправ.

• Чому дорівнює об’єм прямої трикутної призми, в основі якої лежить прямокутний трикутник з катетами 6 см і 8 см, а висота призми дорівнює 10 см?

(Відповідь: 240 см³)

• Обчисліть об’єм піраміди, основою якої є прямокутник зі сторонами 6 см і 10 см, а висота піраміди дорівнює 15 см.

(Відповідь: 300 см³)

• Знайти об’єм та площу поверхні кулі, радіус якої дорівнює 6 см.

(Відповідь: 288π см³, 144π см²)

• Радіус основи циліндра дорівнює 2 см, а висота циліндра – 3 см. Знайти об’єм циліндра та площу його поверхні.

(Відповідь: 12π см³, 16π см²)

• Сторони прямокутника дорівнюють 3 см і 4 см. Знайти площу бічної поверхні циліндра, утвореного в результаті обертання цього прямокутника навколо сторони, що дорівнює 3 см.

(Відповідь: )

Виконання письмових вправ.

1.               Обчислити об’єм куба, площа поверхні якого 150 см².

Розв’язання:

Площа поверхні куба складається з суми площ усіх його граней. Грані куба – квадрати. Їх шість. Об’єм куба дорівнює кубу ребра. Знайдемо довжину ребра куба:

S_п=6S_ABCD;

150 (см²)= 6S_ABCD;

S_ABCD=25 (см²);  (площа однієї грані)

S_ABCD=AB²;

AB²=25 (см²)

AB=5 (см) (довжина ребра)

V_к=AB³=5³=125 (см³).

Відповідь: 125 (см³).

 

2.               Твірна конуса дорівнює 8 см і утворює з площиною основи кут 60°. Знайти площу повної поверхні конуса.

Розв’язання:

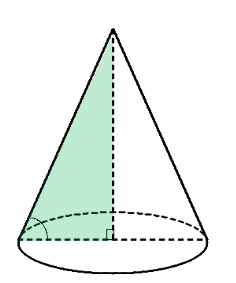Площа повної поверхні конуса складається з площі бічної поверхні та площі основи:

S_п=S_б+S_осн; S_б=πSA AO; S_осн =πAO², де SA – твірна конуса, AO – радіус основи.

Знайдемо його з трикутника SAO:

cos<SAO=AO/SA; AO=SAcos<SAO=SAcos60°=80.5=4 (с).

Тоді S_б=πSA AO= π84=32π (см²),

 S_осн =πAO²=π4²=16π (см²),

S_п=32π (см²)+16π (см²)=48π (см²).

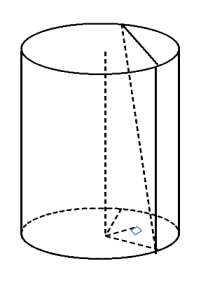3.               У циліндр паралельно його осі на відстані 3 см від неї проведено переріз, діагональ якого 5 см. Обчислити об’єм циліндра, якщо цей переріз перетинає основу по хорді, яка дорівнює 4 см.

Розв’язання:

Об’єм циліндра обчислимо за формулою

V=πOA²BC

OA знайдемо з трикутника OMA за теоремою Піфагора:

OA²=OM²+MA²; MA=AB/2=4 (см); OA²=3²+4²= 25 (см²);

OA=5 (см).

З трикутника ABC знайдемо висоту циліндра BC за теоремою Піфагора: BC²=AC²-AB²=10²-8²=36 (см²); BC=6(см);

Тоді V= π5²6=150 π (см³).

Відповідь:150 π (см³).

 

4.     Чому дорівнює об’єм кулі, якщо площа її великого круга дорівнює 81π см²?

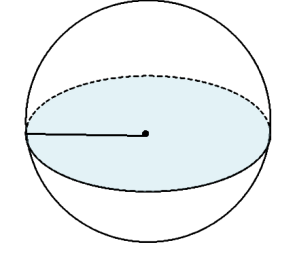Розв’язання:

Великий круг – переріз січною площиною, що проходить через центр кулі. Його площа знаходиться за формулою:

S_в.к.= πAO², де ОФ – радіус кулі. Нам дано, що  S_в.к.= 81π (см²). Запишемо рівність:

πAO²= 81π; з рівності знайдемо, що AO=9 (см);

Тоді:

V_к=

 

Відповідь: 972π (см³).

 

VI. Підсумки уроку.

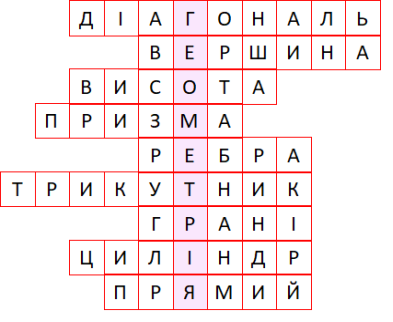
1. Як називається відрізок, що з’єднує дві вершини призми, що не належать одній грані?

2. Точка, в якій перетинаються ребра піраміди 

3. Як називається перпендикуляр,опущений з вершини піраміди на площину її основи 

4. Просторова геометрична фігура

5. Прямі, по яких перетинаються грані призми 

6. Осьовим перерізом конуса є … 

7. Прямокутники,з яких складається паралелепіпед

8. Геометричне тіло, утворене обертанням прямокутника навколо однієї із сторін  

9. Вид кута 

 

VII. Домашнє завдання.

Розв’язати задачі.

1. Сторона основи правильної трикутної призми дорівнює 4 см, висота призми - 6 см. Знайти об’єм призми.
2. Основою піраміди є ромб із діагоналями 6 см і 10 см. Знайти об’єм піраміди, якщо її висота дорівнює 10 см.
3. Знайдіть радіус сфери, якщо її площа дорівнює площі бічної поверхні циліндра з радіусом основи 2 см і висотою 16 см.
4. Через вершину конуса проведено площину, яка відсікає від кола основи його чверть. Знайти площу повної поверхні конуса, якщо радіус основи дорівнює R, а кут у перерізі при вершині конуса дорівнює 60°.
5. Знайдіть об’єм конуса, висота якого дорівнює 12 см, а твірна нахилена до площини основи під кутом 60°.

 

 

Таблиця оцінювання

№ п\п	ПІБ	Контрольні запитання (1 бал)	Усні вправи (3 бали)	Письмові вправи (6 балів)	Кросворд (1 бал)	Всього
1
2
…