Обернена пропорційність. Функція у = k/x, її графік та властивості
Тема. Обернена пропорційність. Функція у = ![]() , її графік та властивості
, її графік та властивості
Мета: формувати уявлення про обернену пропорційність як функцію, навчити будувати її графік, дослідити властивості оберненої пропорційності, порівняти їх з прямою пропорційністю; розвивати вміння i навички знаходження області визначення та області значень функції, логічне мислення та інформаційні компетенції: вміння знаходити, осмислювати та аналізувати інформацію; виховувати інтерес до математики, старанність i працьовитість.
Тип уроку:формування вмінь та навичок.
Обладнання: презентація, комп’ютери, програмне забезпечення «Microsoft Office Excel», опорні конспекти з теми «Функція у = ![]() », порівняльна таблиця.
», порівняльна таблиця.
ХІД УРОКУ
І. Розминка
Перш ніж почати наш урок ми розгадаємо кросворд і дізнаємося про яку фігуру піде мова сьогодні на уроці.
Питання
- Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати відповідають значенням функції.?
- Залежна змінна?
- Один зі способів задання функції?
- Незалежна змінна?
- Як називається вісь у?
- Як називається вісь х?
-
Як називається значення k у формулі
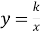 ?
?
- Один зі способів задання функції?
- Один зі способів задання функції?
|
|
Г |
р |
а |
ф |
і |
к |
||||||||
|
ф |
у |
н |
к |
ц |
І |
я |
|
|||||||
|
|
о |
П |
и |
с |
|
|||||||||
|
а |
р |
г |
у |
м |
Е |
н |
т |
|
||||||
|
|
о |
Р |
д |
и |
н |
а |
т |
а |
||||||
|
а |
Б |
с |
ц |
и |
с |
а |
|
|||||||
|
|
к |
О |
е |
ф |
і |
ц |
і |
є |
н |
т |
||||
|
|
т |
а |
б |
Л |
и |
ц |
я |
|
||||||
|
ф |
о |
р |
м |
у |
л |
А |
||||||||
ІІ. Обгрунтування.
ВПРАВА «ДИВУЙ»
Після заповнення кросворда зачитується термін, який вийшов по вертикалі (гіпербола), запитую в учнів, що він означає і даю короткий історичний опис.
Розповідь:
Отримана крива називається гіперболою, що в перекладі із грецької мови дослівно означає «проходжу через що- або» і із часом одержало друге значеннєве значення «перебільшення».
Одним з перших, хто почав вивчати цю криву був учень знаменитого Платона, давньогрецький математик Менехм в IV в. до н.е., але так і не зумів її повністю вивчити.


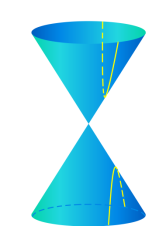 А от повністю досліджував властивості гіперболи й дав їй назву найкращій геометр стародавності Аполоний Пергский в III в. до н.е.
А от повністю досліджував властивості гіперболи й дав їй назву найкращій геометр стародавності Аполоний Пергский в III в. до н.е. 
Він показав, що гіпербола виходить, якщо взяти довільний круговий конус, порожнини якого простираються по обидві сторони від вершини, і перетнути обидві його порожнини площиною, паралельної прямій АА1.
Тепер почасти зрозуміло, чому крива одержала таку назву: ми побачимо її в перетині щораз, коли площина проходить через обидві порожнини конуса.
ІІІ.АКТУАЛІЗАЦІЯ.
Вправа Знаємо- Хочемо дізнатися – Дізналися
Спочатку пригадаємо, що ми знаємо про пряму та обернену пропорційність нарівні понять.
- Що називається прямою пропорційністю?
Залежність між двома величинами, за якої вони одночасно збільшуються або зменшуються.
- Що називається оберненою пропорційністю?
Залежність між двома величинами, за якої зі збільшенням однієї величини зменшується інша, i навпаки.
-
Визначте вид залежності:
- довжина сторони квадрата i його периметр;
- обсяг виконаного домашнього завдання i отримана оцінка;
- змарнований час i обсяг виконаної роботи;
- оцінки в щоденнику i радість батьків.
Розглянемо прояви оберненої пропорційності у явищах природи та галузях людської діяльності. Цим ми ще раз підтвердимо слова Г. Галілея: «Природа формулює свої закони мовою математики».
Цей вислів можна вважати епіграфом нашого уроку.
Вправа « САМ СОБІ ВЧИТЕЛЬ»
А зараз прослухаємо звіт учнів про виконану пошукову роботу (виконуючи роботу, вони звертались за рекомендаціями до «Довідника школяра»)
- Обернена пропорційність у біології:
У біології можна знайти багато прикладів оберненопропорційних залежностей: Наприклад, чисельність особин певного виду на деякій території i кількість корму, розміри тварин та їхня рухливість (наприклад, порівняємо ящірку i варана, слона та мишку); розміри тварин та їх плодючість (маленькі тварини дають більше потомства, ніж великі)| діаметр кровоносних судин і тиск крові (із звуженням судин тиск крові збільшується).
2. Обернена пропорційність у фізиці:
1) Залежність тиску від площі поверхні
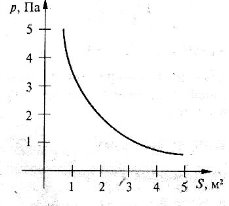 Ця залежність описується графіком p =
Ця залежність описується графіком p = ![]()
Тиск, який чинить тіло на деяку поверхню, обернено пропорційний до площі цієї поверхні.
За графіком бачимо, що із збільшенням площі поверхнізменшується тиск на неї, i навпаки.
Наприклад, людині важко йти по пухкому снігу, вона провалюється на кожному кроці. Але на лижах можна йти по снігу, майже не провалюючись у нього. Сила, з якою людина діє на сніг, в обох випадках однакова, проте різна площа поверхні на яку тисне людина на лижах i без них.
 Леза різальних івістря колючих інструментів(ножів, ножиць, різців, пилок, голок тощо) добре загострюють. Гостре лезо має маленьку площу, тому навіть від малої сили створюється великий тиск,ітаким інструментом легко працювати.
Леза різальних івістря колючих інструментів(ножів, ножиць, різців, пилок, голок тощо) добре загострюють. Гостре лезо має маленьку площу, тому навіть від малої сили створюється великий тиск,ітаким інструментом легко працювати.
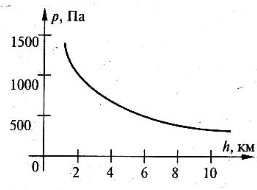
2) Залежність атмосферного тиску від висоти над поверхнею землі
Із збільшенням висоти над рівнем моря зменшуються тиск і температура повітря.
Таке зменшення відбувається поступово: Залежність атмосферного тиску від висоти над поверхнею землі вперше відкрив Блез Паскаль. Група його учнів піднялась на гору То – де – Дом (Франція) і виявила, що на вершині гори стовп ртуті на 7,5 см коротший ніж біля її підніжжя.
3) Залежність між швидкістю і часом
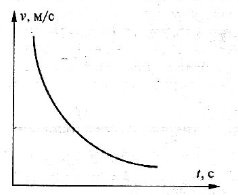
Певну відстань із більшою швидкістю можна проїхати за менший час, за умови зменшення швидкості їхати доведеться довше. Отже, швидкість i час обернено пропорційні величини.
4) Закон Ома для ділянки кола
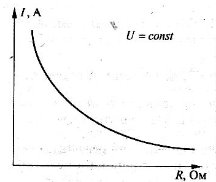
Сила струму на ділянці кола прямо пропорційна напрузі на кінцях цієї ділянки i обернено пропорційна її опору (закон Ома для ділянки кола).
3.Обернена пропорційність в економіці
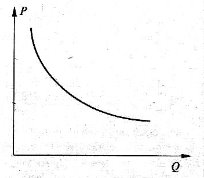
В економіці прикладом оберненої пропорційності є закон попиту: якщо ціна якогось товару підвищується i при цьому решта умов залишається незмінними, попитом буде користуватися менша кількість цього товару.
ІV. УСВІДОМЛЕННЯ ЗМІСТУ
Узагальнивши всі формули, можна записати формулу оберненоїпропорційності:у =![]() , де
, де![]() – сталий коефіцієнт, у– залежна величина (значення функції), х– аргумент функції.
– сталий коефіцієнт, у– залежна величина (значення функції), х– аргумент функції.
- № 340(усно)
-
Побудуємо графік функції у =

|
х |
– 6 |
–3 |
–2 |
–1 |
1 |
2 |
3 |
6 |
|
у |
–1 |
–2 |
–3 |
–6 |
6 |
3 |
2 |
1 |
Висновок: - область визначення функції складається з усіх чисел, крім 0;
- область значень функції складається з усіх чисел, крім 0
-
графік функції називається гіпербола, вітки якої розміщені в І і ІІІ координатних чвертях, якщо
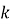 > 0, і в ІІ та ІV, якщо
> 0, і в ІІ та ІV, якщо 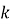 < 0.
< 0.
- вітки гіперболи необмежено наближаються до осей координат.
Графік оберненої пропорційності називається гіперболою. Де ще ви зустрічалися з таким терміном? Що він означає?
-
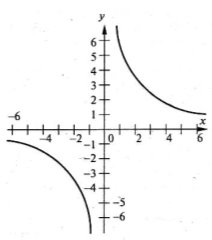 Побудуємо графік функції у =–
Побудуємо графік функції у =– . (№ 347)
. (№ 347)
(група учнів будує графік за комп’ютерами)
|
х |
– 8 |
–4 |
–2 |
–1 |
1 |
2 |
4 |
8 |
|
у |
1 |
2 |
4 |
8 |
–8 |
–4 |
– 2 |
– 1 |
- Графічний метод розв’язування рівнянь.
За допомогою графіків функцій можна розв’язувати рівняння, які аналітично розв’язати важко. Розв’яжемо рівняння ![]() = 2х. Для цього побудуємо графіки функцій у =
= 2х. Для цього побудуємо графіки функцій у = ![]() та у = 2х в одній системі координат. (Відповідь: х =–2; х = 2)
та у = 2х в одній системі координат. (Відповідь: х =–2; х = 2)
Отже, щойно ми розглянули один з видів практичного застосування даної теми.
V. РЕФЛЕКСІЯ
Створення порівняльної таблиці
Порівняльна таблиця графіків прямої та оберненої пропорційності
|
Характеристика функції |
Пряма пропорційність |
Обернена пропорційність |
|
Формула |
у = |
у = |
|
Область визначення |
всі числа |
х ≠ 0 |
|
Область значень |
всі числа |
у ≠ 0 |
|
Графік |
пряма |
гіпербола |
|
|
І і ІІІ чверть, зростає |
І і ІІІ чверть, спадає |
|
|
ІІ і ІV чверть, спадає |
ІІ і ІV чверть, зростає |
|
Перетин з осями координат |
перетинає |
не перетинає |
VІ.ДОМАШНЄ ЗАВДАННЯ
У завданнях 1-4 виберіть одну правильну відповідь і позначте її в бланку відповідей
1. В яких координатних чвертях розташований графік функції у = ![]() ?
?
А) I, IV; Б) I, II; В) II, IV; Г) I, III.
2. Знайдіть значення функції y = - y = - ![]() . , якщо x = 2,5.
. , якщо x = 2,5.
А) -4; Б) 0,4; В) -0,4; Г) 4.
3. Які з наведених функцій є оберненою пропорційністю?
А) у = ![]() ; Б) у =
; Б) у = ![]() + х; В) у =
+ х; В) у = ![]() ; Г) у = -
; Г) у = - ![]() .
.
4. Знайдіть значення аргументу, при якому значення функції ![]() дорівнює - 3.
дорівнює - 3.
А) – 4; Б) 4; В) 2; Г) – 2.
Завдання 5 передбачають установлення відповідності. До кожного твердження, позначеного цифрою, виберіть твердження, позначене буквою і зробіть і поставте позначки на перетині відповідних рядків (цифри) і стовпчиків (букви).
5. Установіть відповідність між графіками функцій (1 – 4) і точками, які їм належать (А – Д).
|
1) у = - |
А) (- 12;2) |
|
2) у = |
Б) (-2; 5) |
|
3) у = - |
В) (10; - 1,5) |
|
4) у = |
Г) (8;1) |
|
|
Д) (4;4) |
-
Дуже цікавий урок! Дякую!
-
Цікаві розробки уроків! Успіхів Вам!


про публікацію авторської розробки
Додати розробку
