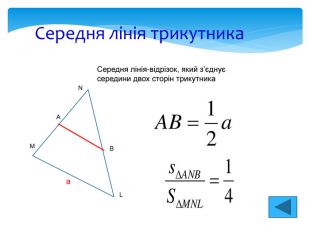
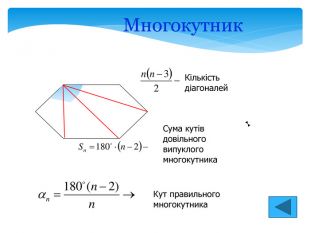
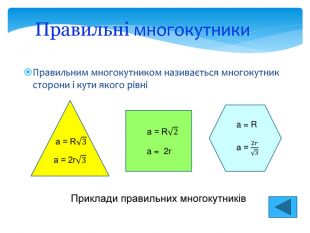
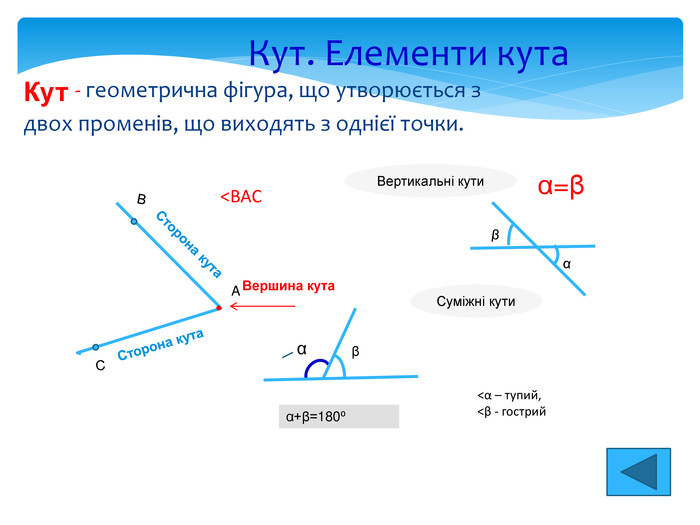
Опорні факти планіметрії

Зміст

Кут. Елементи кута - геометрична фігура, що утворюється з двох променів, що виходять з однієї точки. Вершина кута Сторона кута α β α=β α α+β=180⁰ Сторона кута Вертикальні кути Суміжні кути β Кут A B C

Знайдіть градусну міру невідомого кута під знаком запитання 46⁰ 104⁰ ? 150⁰

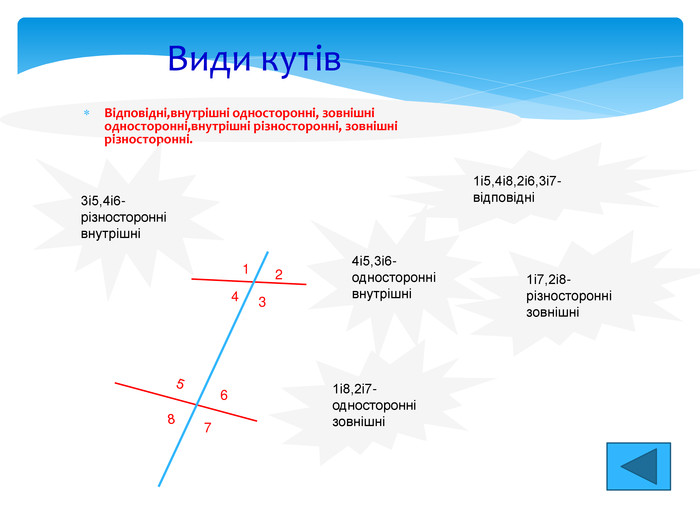
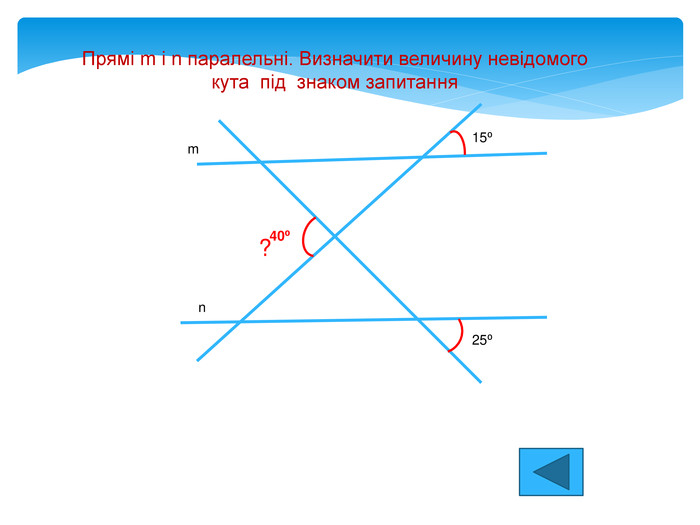
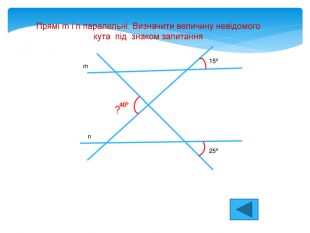
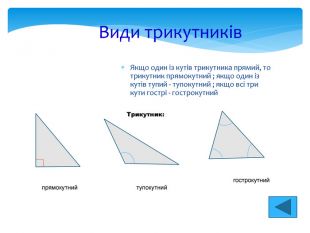
Види кутів Відповідні,внутрішні односторонні, зовнішні односторонні,внутрішні різносторонні, зовнішні різносторонні. 1 2 3 4 5 6 7 8 1і5,4і8,2і6,3і7- відповідні 3і5,4і6- різносторонні внутрішні 1і7,2і8- різносторонні зовнішні 4і5,3і6- односторонні внутрішні 1і8,2і7- односторонні зовнішні

Кути з відповідно перпендикулярними сторонами Або рівні,або їх сума дорівнює 180⁰ α β α+β=180⁰ α β α=β

Ознаки паралельних прямих. Якщо при перетині двох прямих третьою : 1) різносторонні кути рівні,або 2)відповідні кути рівні, або 3)сума односторонніх кутів дорівнює 180⁰, то прямі паралельні а b 7 aІІb 1 2 3 4 5 6 8

Прямі m і n паралельні. Визначити величину невідомого кута під знаком запитання 15⁰ 25⁰ m n ? 40⁰

Трикутник. Елементи трикутника Фігура, яка складається із трьох відрізків АВ, ВС, АС , називається трикутником ABC (позначається: Δ ABC) A B C Сума довжин усіх сторін трикутника називається його периметром. А,В,С- вершини АВС, ВАС, ВСА – кути трикутника

Нерівність трикутника Довжина кожної сторони трикутника менша, ніж сума, і більша, ніж різниця довжин двох інших сторін трикутника а в с

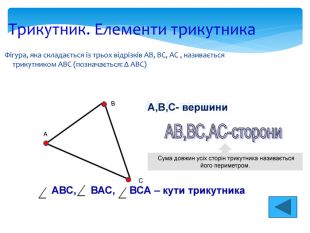
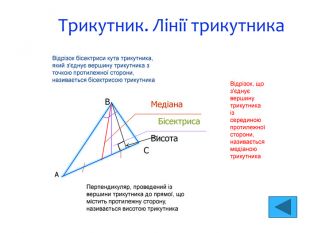
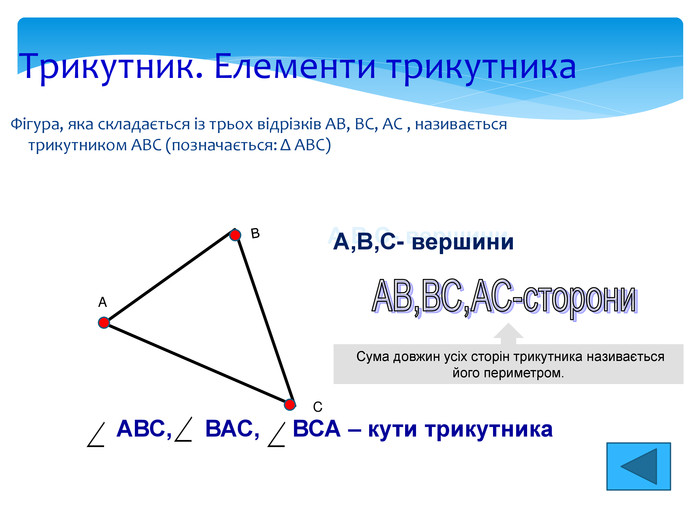
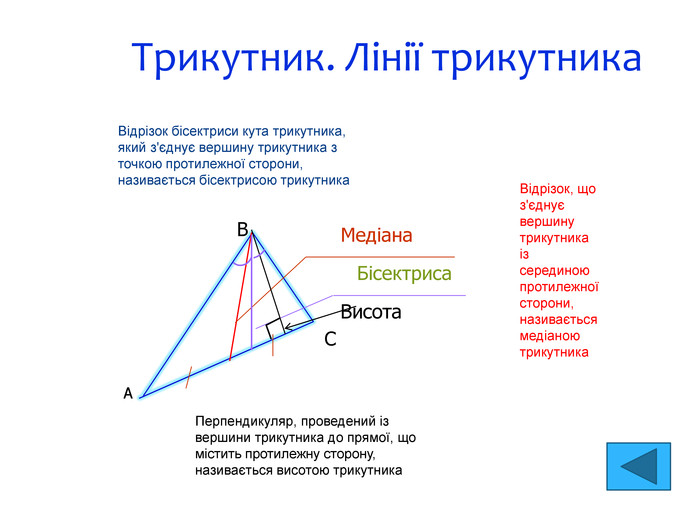
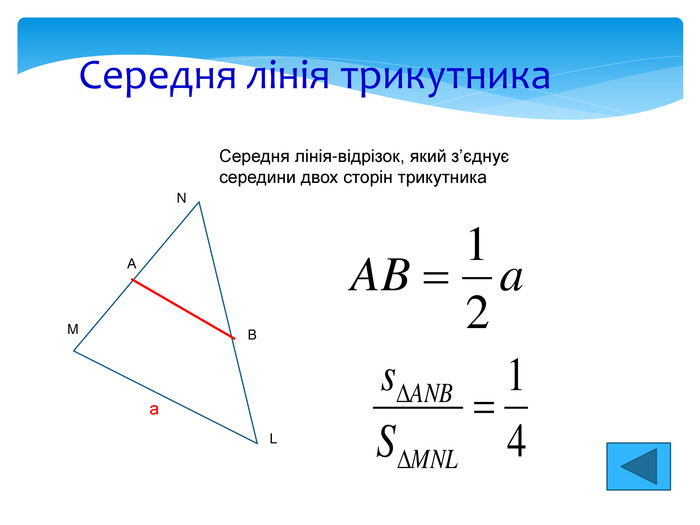
Трикутник. Лінії трикутника Медіана Бісектриса Висота В С A Відрізок бісектриси кута трикутника, який з'єднує вершину трикутника з точкою протилежної сторони, називається бісектрисою трикутника Відрізок, що з'єднує вершину трикутника із серединою протилежної сторони, називається медіаною трикутника Перпендикуляр, проведений із вершини трикутника до прямої, що містить протилежну сторону, називається висотою трикутника

Властивості медіани Медіани точкою перетину діляться у відношенні 2:1, рахуючи від вершини Медіана ділить трикутник на два трикутника з рівними площами. Три медіани трикутника перетинаються в одній точці і при цьому утворюються шість трикутників, площі яких рівні. а b c 1 2

Властивість бісектриси трикутника Бісектриса кута трикутника ділить протилежну сторону у відношенні рівному відношенню двох прилеглих сторін a b c d l Бісектриси внутрішнього і зовнішнього кутів перпендикулярні

Середня лінія трикутника Середня лінія-відрізок, який з’єднує середини двох сторін трикутника а А B M N L

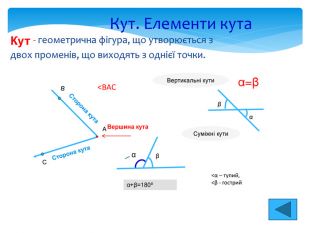
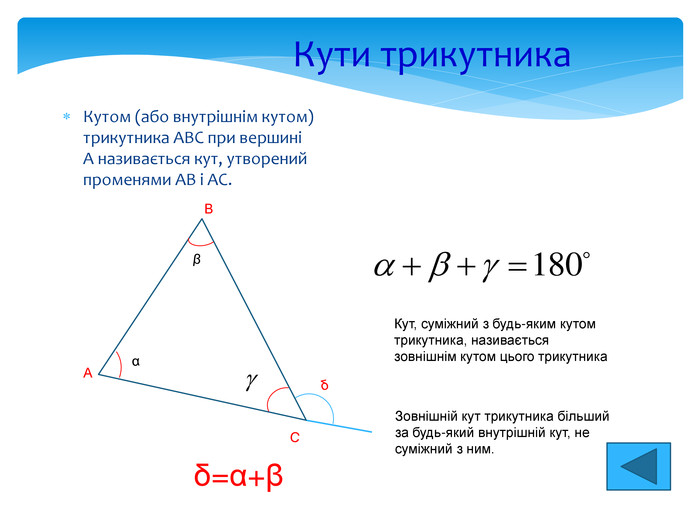
Кути трикутника Кутом (або внутрішнім кутом) трикутника ABC при вершині А називається кут, утворений променями АВ і АС. Кут, суміжний з будь-яким кутом трикутника, називається зовнішнім кутом цього трикутника δ δ=α+β С А В β α Зовнішній кут трикутника більший за будь-який внутрішній кут, не суміжний з ним.

Види трикутників Якщо один із кутів трикутника прямий, то трикутник прямокутний ; якщо один із кутів тупий - тупокутний ; якщо всі три кути гострі - гострокутний прямокутний тупокутний гострокутний Трикутник:

Рівнобедрений трикутник Трикутник, дві сторони якого рівні, називається рівнобедреним . Третя сторона - основа, рівні сторони - бічні сторони. β α R r a b

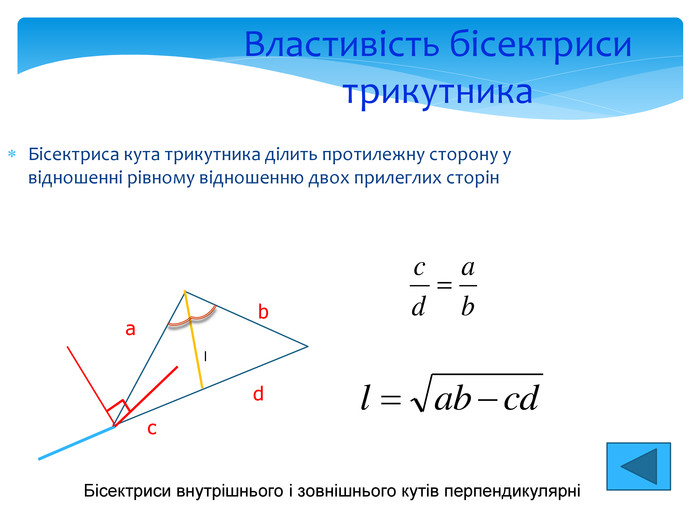
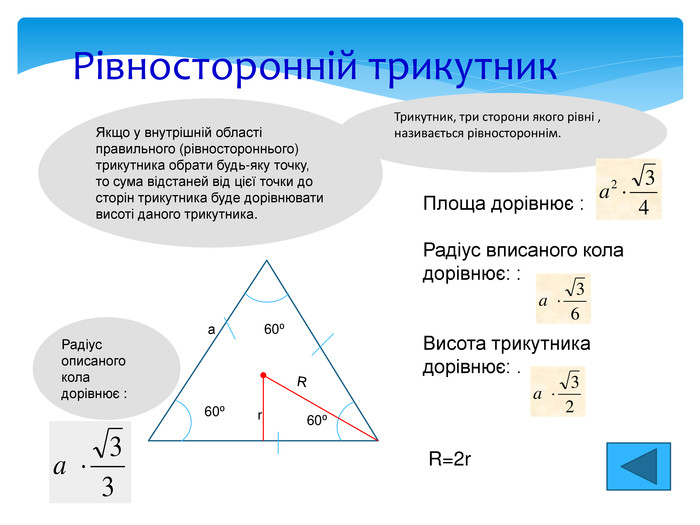
Рівносторонній трикутник Трикутник, три сторони якого рівні , називається рівностороннім. Площа дорівнює : Радіус вписаного кола дорівнює: : Висота трикутника дорівнює: . Якщо у внутрішній області правильного (рівностороннього) трикутника обрати будь-яку точку, то сума відстаней від цієї точки до сторін трикутника буде дорівнювати висоті даного трикутника. Радіус описаного кола дорівнює : R=2r 60⁰ 60⁰ 60⁰ а R r

Теорема Піфагора. Співвідношення в прямокутному трикутнику А В С с b а

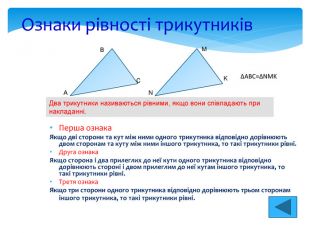
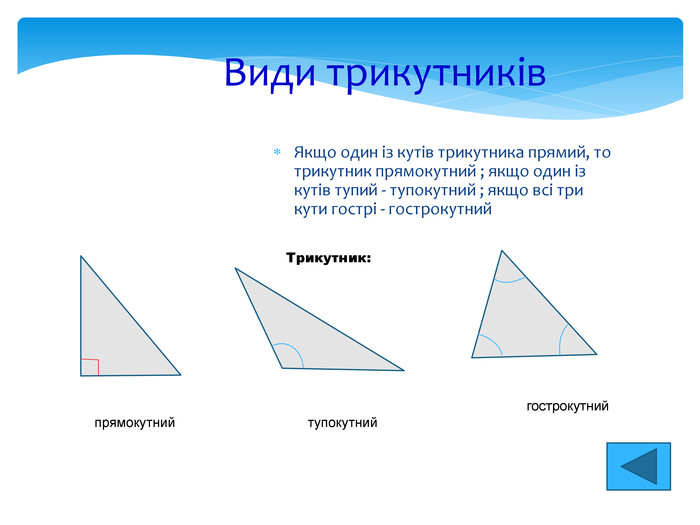
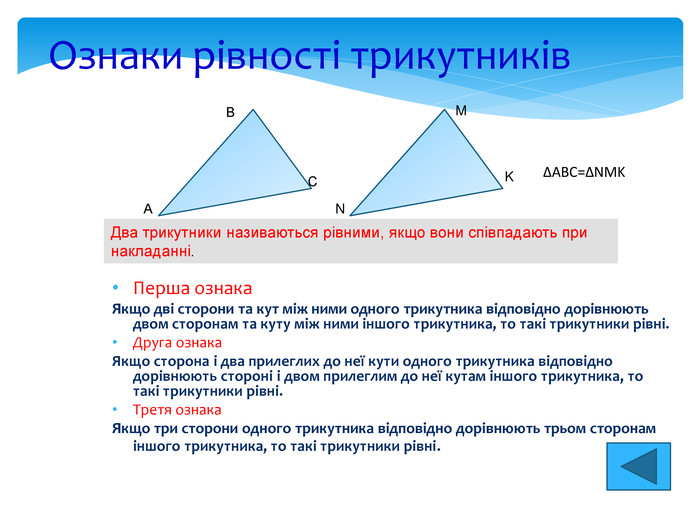
Перша ознака Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам та куту між ними іншого трикутника, то такі трикутники рівні. Друга ознака Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні. Третя ознака Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні. Ознаки рівності трикутників Два трикутники називаються рівними, якщо вони співпадають при накладанні. А В С M N K ∆ABC=∆NMK

Ознаки подібності трикутників Два трикутники подібні, якщо кути одного трикутника відповідно дорівнюють кутам іншого трикутника та сторони одного пропорційні відповідним сторонам іншого. 1) Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні. 2)Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника та кути, утворені цими сторонами, рівні, то такі трикутники подібні. 3) Якщо три сторони одного трикутника пропорційні трьом сторонам іншого трикутника, то такі трикутники подібні.

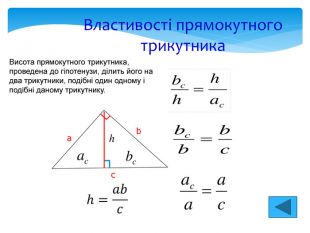
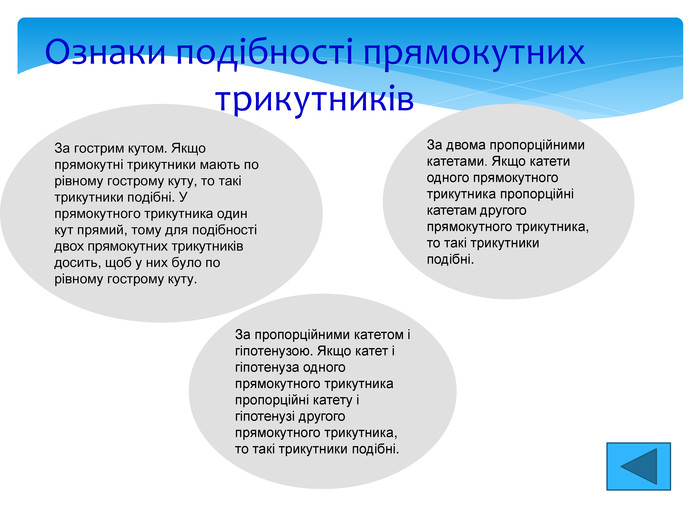
Ознаки подібності прямокутних трикутників За гострим кутом. Якщо прямокутні трикутники мають по рівному гострому куту, то такі трикутники подібні. У прямокутного трикутника один кут прямий, тому для подібності двох прямокутних трикутників досить, щоб у них було по рівному гострому куту. За двома пропорційними катетами. Якщо катети одного прямокутного трикутника пропорційні катетам другого прямокутного трикутника, то такі трикутники подібні. За пропорційними катетом і гіпотенузою. Якщо катет і гіпотенуза одного прямокутного трикутника пропорційні катету і гіпотенузі другого прямокутного трикутника, то такі трикутники подібні.

Властивості прямокутного трикутника a b c Висота прямокутного трикутника, проведена до гіпотенузи, ділить його на два трикутники, подібні один одному і подібні даному трикутнику.

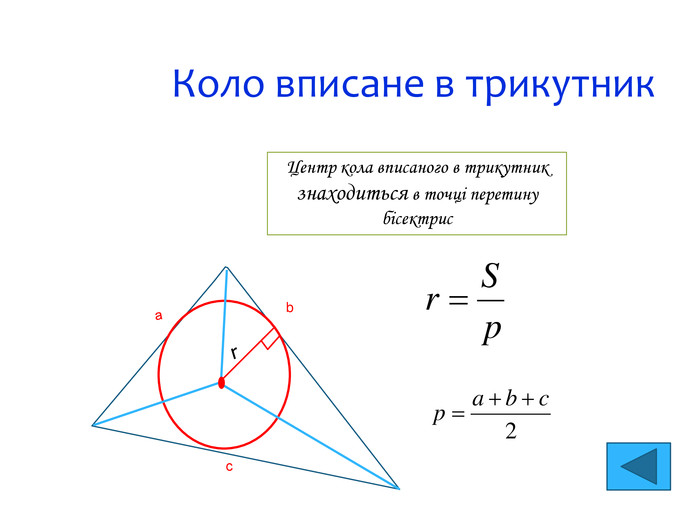
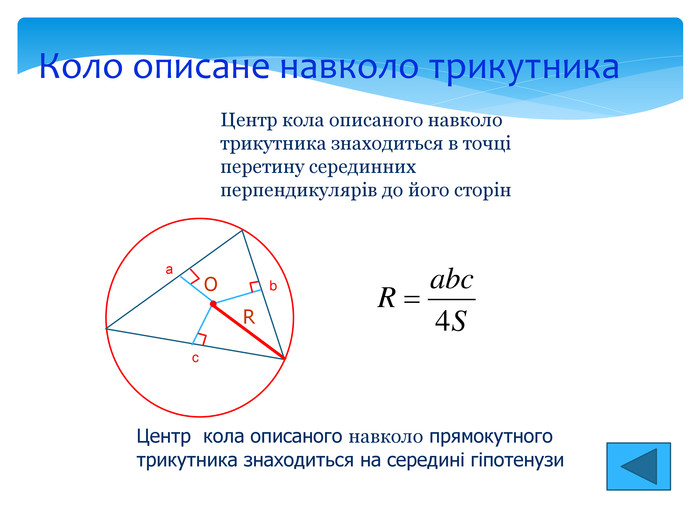
Трикутник та його площа А В С а b с D Якщо основи двох трикутників рівні, то відношення площ цих трикутників дорівнює відношенню їх висот. І навпаки, якщо у двох трикутників висоти рівні, то відношення їх площ дорівнює відношенню їх основ. S=pr r – радіус вписаного кола R- радіус описаного кола

Теорема синусів C R – радіус описаного кола навколо трикутника A B a b c α β γ c=2Rcosγ Якщо α>β, то a>b; якщо a>b, то α>β. Наслідки:

Теорема косинусів A B C a b c α β γ Наслідок:

Коло вписане в трикутник r Центр кола вписаного в трикутник знаходиться в точці перетину бісектрис а b с

Коло описане навколо трикутника О R Центр кола описаного навколо трикутника знаходиться в точці перетину серединних перпендикулярів до його сторін Центр кола описаного навколо прямокутного трикутника знаходиться на середині гіпотенузи а b c

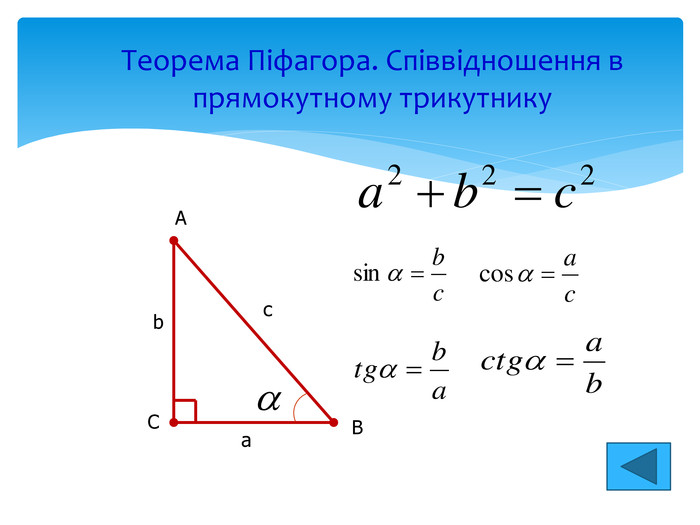
Задачі на повторення по темі “Трикутник” Приклад 1. Довжини катетів прямокутного трикутника дорівнюють 5 і 12. Обчислити довжину гіпотенузи трикутника. Приклад 2. Довжина гіпотенузи прямокутного трикутника дорівнюЄ 13, а одного з катетів – 5. Обчислити довжину другого катета. Приклад 3. Довжини сторін трикутника дорівнюють 17, 17 і 30. Знайти медіану трикутника, що опущена на більшу сторону. Приклад 4. Бічна сторона рівнобедреного трикутника дорівнює 15, а довжина медіани, опущеної на основу, – 9. Знайти основу трикутника. Приклад 5. Сторони трикутника дорівнюють 5, 7 і 10. Обчислити периметр трикутника, вершинами якого є середини сторін даного трикутника Приклад 6. У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки довжиною 5 і 12. Обчислити довжину більшого катета трикутника.

Задачі на повторення по темі “Трикутник” Приклад 7. Медіана, опущена на гіпотенузу прямокутного трикутника, дорівнює 5, а один з катетів – 6. Знайти радіус вписаного кола. Приклад 8. У прямокутний трикутник з катетами 3 і 7 вписано квадрат, що має з трикутником спільний прямий кут. Обчислити периметр квадрата. Приклад 9. Площа рівностороннього трикутника дорівнює 123 . Обчислити радіус кола, описаного навколо цього трикутника. Приклад 10. Довжини сторін трикутника дорівнюють 2, 4 і 5. Обчислити косинус кута трикутника, що лежить навпроти найменшої сторони. Приклад 11. Площа рівностороннього трикутника дорівнює 273 . Обчислити радіус кола, вписаного у цей трикутник.

Чотирикутник A B C D d1 d2 Якщо чотирикутник є і вписаним ,і описаним в коло, то: а b c d α

Чотирикутник вписаний в коло A B C D Чотирикутник є вписаним тоді й тільки тоді, коли сума його протилежних кутів дорівнює 180 ⁰ Також кути, що спираються на одну й ту ж сторону, рівні, зокрема: 180⁰ Теорема Птоломея ;

Чотирикутник описаний навколо кола a b c d Чотирикутник є описаним тоді й тільки тоді, коли суми довжин його протилежних сторін рівні. a+c=b+d O r p - півпериметр

Паралелограм B A C D M Паралелограмом називається чотирикутник у якого протилежні сторони паралельні

Трапеція Відрізок, який сполучає середини бічних сторін, називається B C a b Середня лінія паралельна основам трапеції, а її довжина дорівнює їх півсумі: Навколо рівнобічної трапеції можна описати коло. Якщо сума основ трапеції дорівнює сумі її бокових сторін, то в таку трапецію можна вписати коло, і навпаки. середньою лінією трапеції A h D

Ромб A B C D O М r a

Коло вписане в ромб a r В ромб можна вписати коло, бо суми довжин протилежних сторін рівні.

Чи є ці фігури паралелограмами? Прямокутник — паралелограм, всі кути якого прямі; Ромб — паралелограм, всі чотири сторони якого рівні між собою; Квадрат — рівнобічний прямокутник. S= ab a a b

Площі подібних фігур Площі подібних фігур відносяться як квадрати їх лінійних розмірів. A B C M N ∆МАN ~∆BAC

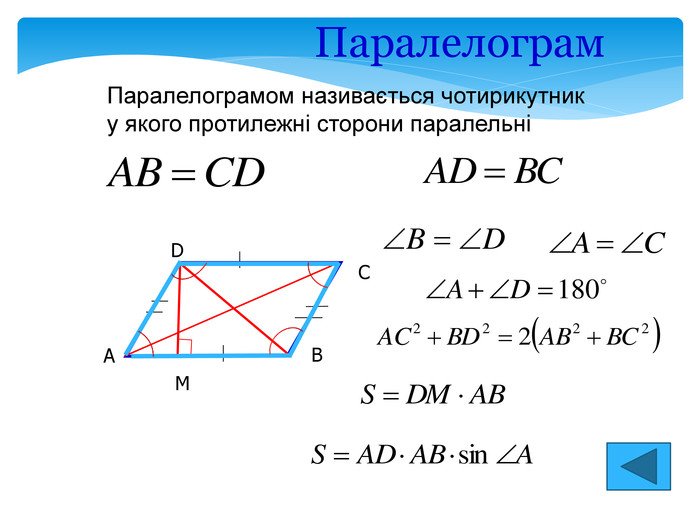
Задачі на повторення теми “Чотирикутник” Приклад 1. У чотирикутнику діагоналі дорівнюють 8 і 5. Обчислити периметр чотирикутника, вершинами якого є середини сторін даного чотирикутника. Приклад 2. У чотирикутнику ABCD діагоналі AC = 5 і BD = 8 є взаємо перпендикулярними. Обчислити площу чотирикутника ABCD. Приклад 3. У паралелограмі ABCD через точку перетину діагоналей проведено пряму, яка відтинає на сторонах BC і AD відрізки BE = 5 і AF = 7. Обчислити сторону BC. Приклад 4. У паралелограмі ABCD через точку перетину діагоналей проведено пряму, яка відтинає на сторонах BC і AD відрізки BE і AF. Обчислити довжину відрізка BE, якщо AF = 6 і AD = 11. Приклад 5. У паралелограмі ABCD проведено бісектрису кута A, яка перетинає сторону BC в точці E. Обчислити довжину відрізка BE, якщо AB = 6. Приклад 6. Довжини діагоналей паралелограма дорівнюють 2 і 4, а кут між ними – 30⁰ . Обчислити площу паралелограма.

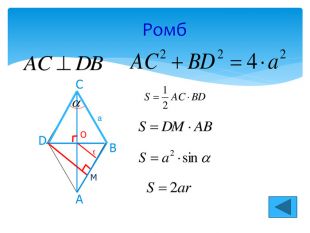
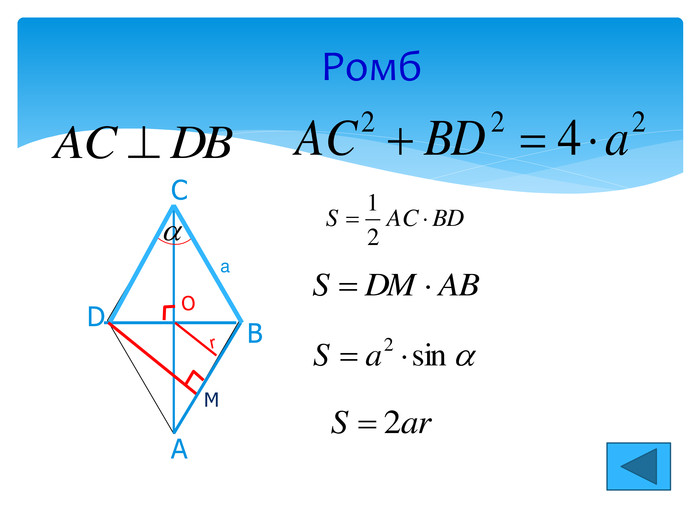
Задачі на повторення теми “Чотирикутник” Приклад 7. Довжини діагоналей паралелограма дорівнюють 4 3 і 7, а кут між ними – 60⁰ . Обчислити площу паралелограма. Приклад 8. Периметр прямокутника дорівнює 36. Обчислити суму відстаней від будь-якої точки всередині цього прямокутника до всіх його сторін. Приклад 9. Бісектриса одного з кутів прямокутника ділить його сторону навпіл. Знайти периметр прямокутника, якщо його менша сторона дорівнює 5. Приклад 10. Довжина сторони ромба дорівнює 17, а однієї з діагоналей – 30. Обчислити довжину другої діагоналі. Приклад 11. Середня лінія трапеції дорівнює 19, а одна з основ – 16. Обчислити довжину другої основи трапеції. Приклад 12. Дано квадрат, сторона якого дорівнює 6. Діагональ його дорівнює стороні другого квадрата. Обчислити діагональ другого квадрата.

Коло. Круг R O Хорда Дотична Січна l

Кути вписані в коло O A C B Вписаний кут Центральний кут

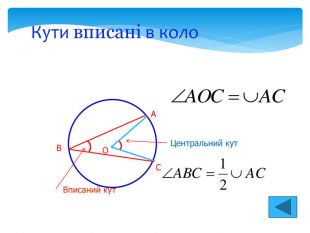
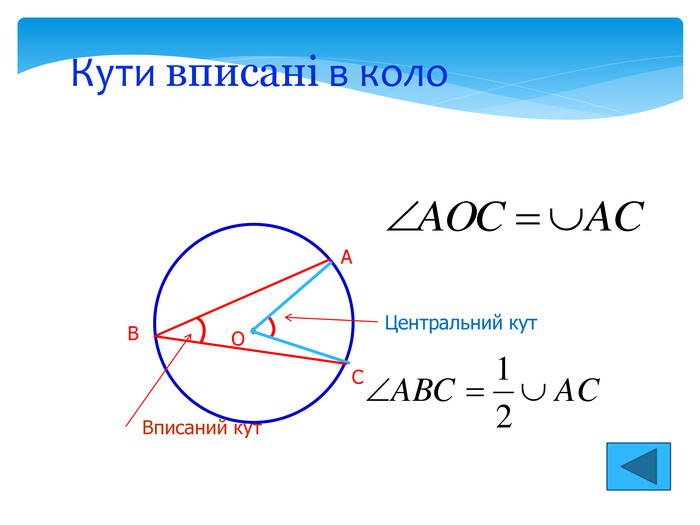
1. Центральний кут дорівнює 40⁰,чому дорівнює вписаний кут? 2. Вписаний кут дорівнює 45⁰,чому дорівнює центральний кут? 3. Який центральний кут більший від відповідного йому вписаного на 70⁰? 4. Вписаний кут прямий, яким є відповідний йому центральний кут? 5. Вписаний кут спирається на діаметр кола, яким є відповідний йому центральний кут? 6. Коло з центром О точками А, В, С поділено на 3 рівні дуги, знайдіть міри кутів АОС, АВС. Усні вправи

1. Центральний кут дорівнює 40⁰,чому дорівнює вписаний кут? 2. Вписаний кут дорівнює 45⁰,чому дорівнює центральний кут? 3. Який центральний кут більший від відповідного йому вписаного на 70⁰? 4. Вписаний кут прямий, яким є відповідний йому центральний кут? 5. Вписаний кут спирається на діаметр кола, яким є відповідний йому центральний кут? 6. Коло з центром О точками А, В, С поділено на 3 рівні дуги, знайдіть міри кутів АОС, АВС. Усні вправи

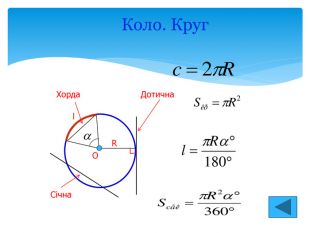
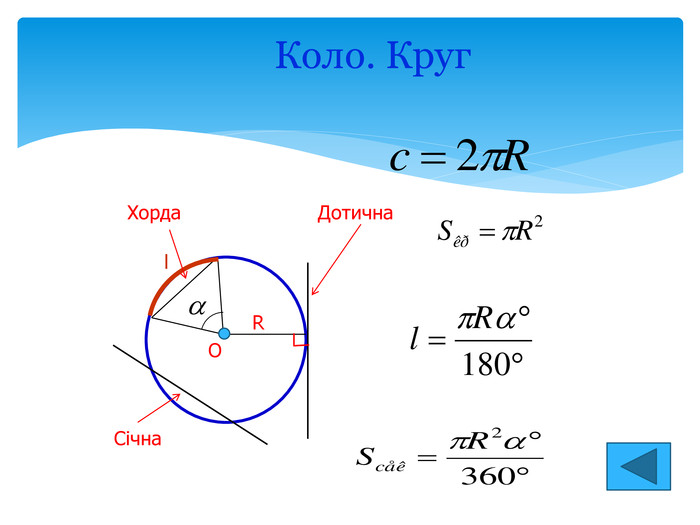
Сектор. Сегмент Сектором називається частина круга, обмежена двома його радіусами. центральний кут. Частина круга, обмежена хордою і стягуваною нею дугою, називається сегментом. Площа сегмента обчислюється як різниця площі сектора, обмеженого радіусами OA і OB, і площі трикутника OAB. A B O R R

Многокутник Кількість діагоналей Сума кутів довільного випуклого многокутника Кут правильного многокутника

Правильні многокутники Правильним многокутником називається многокутник сторони і кути якого рівні a = 2r a = R Приклади правильних многокутників

Площа правильного многокутника Сторона правильного n – кутника дорівнює: Площа правильного n – кутника дорівнює: