Довідничок-помічничок "Найпростіші перетворення радикалів"
Даний матеріал допоможе компактно повторити матеріал по темі "Найпростіші перетворення радикалів". Наведені розв'язані приклади, які показують як вносити під радикал та виносити.
Найпростіші перетворення радикалів.
Означення тотожних ірраціональних виразів і тотожного перетворення залишається таким же, як і для раціональних виразів. Для виконання обчислень важливо вміти користуватися вище наведеними рівностями справа на ліво.
-
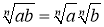 ,
, 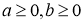 і
і 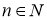 .
.
-
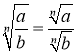 ,
, 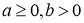 і
і 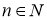 .
.
-
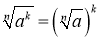 ,
, 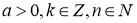 .
.
-
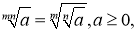 m,n – натуральні числа.
m,n – натуральні числа.
-
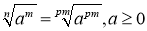 , m,n,p – натуральні числа.
, m,n,p – натуральні числа.
-
 m,n–натуральні числа.
m,n–натуральні числа.
Користуючись цими властивостями, можна добути корінь із різних виразів.![]()
Приклади: 1. а).![]()
б).![]()
2. a).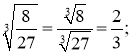
б).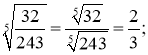
3. a).![]()
б).![]()
4. a).![]()
б). ![]()
5. a). ![]()
б). 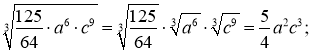
в). 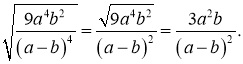
Винесення множника за знак радикала.
Якщо підкореневий вираз розкладається на такі множники, що з деяких можна добути точний корінь, то такі множники, після добування з них кореня можуть бути написані перед знаком кореня (тобто можуть бути винесені за знак кореня). Таке перетворення називають винесенням множника за знак радикала. Таке перетворення можна виконати, використовуючи формулу: ![]()
![]() .
.
Приклади: а). ![]()
б). ![]()
в). ![]()
Примітка. Якщо а від’ємне і n – парне, рівність ![]() невірна, але при будь-яких значеннях a, b, n:
невірна, але при будь-яких значеннях a, b, n: ![]() .
.
Приклади. Винести множник за знак радикала, враховуючи допустимі значення букв або обмежування на них:
a). ![]() при
при ![]()
б). ![]() при
при ![]()
в). 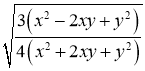
Розв’язок:
а). ![]()
б). ![]()
в). 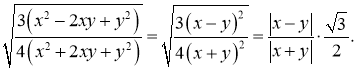
Внесення множника під знак радикала.
Для внесення під знак кореня множників, які стоять перед ним, достатньо піднести такі множники в степінь, показник якого дорівнює показнику кореня, а потім написати результат під знаком кореня. Це виконується за формулою:
![]()
Приклад 1. 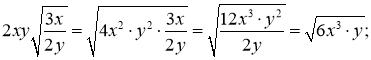
Приклад 2. 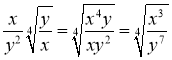
Приклад 3. 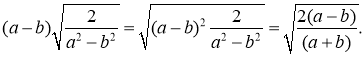
В прикладах 1-3 всі множники перед радикалами вважаються додатними. Приклад 4. Внести множники під знак радикала при заданих значеннях букв:
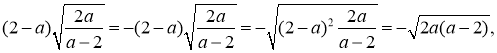 якщо
якщо ![]() Приклад 5. Не добуваючи кореня, визначити яке з чисел більше:
Приклад 5. Не добуваючи кореня, визначити яке з чисел більше: ![]() чи
чи ![]() Розв’язок:
Розв’язок:![]()
![]() Так як
Так як ![]() то
то ![]()
Зведення до раціонального вигляду членів дробово-раціональних виразів.
Використовуючи два попередніх перетворення радикалів, можна звільнитися від радикалів у знаменнику, або чисельнику.
Приклад 6. Звільнитися від ірраціональності в знаменнику:
а) ![]() б)
б) ![]() в)
в)![]()
Розв'язок: а) Щоб в першому радикалі із знаменника можна було б добути квадратний корінь, помножимо чисельник і знаменник дробу на 7:
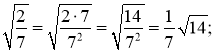
б) Щоб в другому радикалі із знаменника можна було б добути кубічний корінь, помножимо чисельник і знаменник дробу на 32:
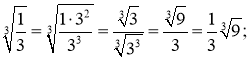
в) Щоб в третьому радикалі із знаменника можна було б добути корінь четвертого степеня, помножимо чисельник і знаменник дробу на 2:
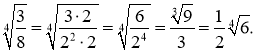
Якщо підкореневий вираз – алгебраїчний дріб, подібні приклади розв’язують аналогічно.
Приклади. a). 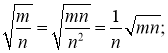
б). 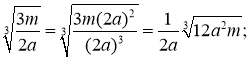
в).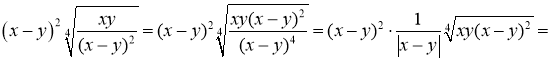
![]()
Примітка. Останній приклад можливо розв’язати і іншим способом:
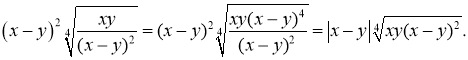


про публікацію авторської розробки
Додати розробку
