Опорний конспект із теми "Тіла обертання"

Тіло обертання

Означення

Рисунок

Формули:

Площа бічної поверхні

Площа повної поверхні

Об’єм

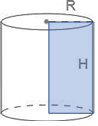
Циліндр

Тіло обертання, яке виходить при обертанні прямокутника навколо однієї зі сторін.

Тіло, яке складається з двох кругів, які суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають відповідні точки кіл кругів, – твірними циліндра.

S_біч = 2πRH,

де R – радіус основи циліндра, а H – висота циліндра.

Sповн = Sбіч + 2Sосн.

S_повн = 2πRH + 2 πR²

S_повн = 2πR(H+R)

V= S_осн.H

V=πR²H

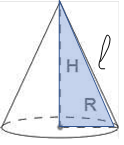
Конус

Тіло обертання, яке виходить при обертанні прямокутного трикутника навколо однієї зі сторін.

Тіло, яке складається із круга – основи конуса; точки, яка не лежить у площині цього круга, – вершини конуса та всіх

Площею бічної поверхні конуса є площа її розгортки.

Розгорткою   бічної поверхні конуса є круговий сектор.

Sповн.=Sбіч.+Sкола 

S_повн.=πRl+πR²

S_повн.= πR(l+R)

Об'єм конуса дорівнює одній третій добутку площі його основи на висоту:

𝑉 = 𝑆кола ⋅ 𝐻

𝑉 = 𝜋𝑅²𝐻

відрізків, що сполучають вершину конуса з точками основи.

Твірні конуса – це відрізки, що з'єднують вершину з точками основи.

Висота     конуса     –      це

перпендикуляр, проведений з вершини до центра основи.

Площа            бічної             поверхні конуса дорівнює половині добутку довжини кола основи на твірну:

S_біч = πRl, де l – твірна, R – радіус основи конуса.

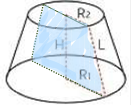
Зрізаний конус

Тіло обертання, яке виходить при обертанні прямокутної трапеції навколо меншої бічної сторони.

Осьовим перерізом зрізаного конуса, є рівнобедрена трапеція.

S=π(R₁+R₂)L,

де R1 і R2 − радіуси основ зрізаного конуса, 

L – твірна

Sповн.=Sбіч.+Sкола1+ Sкола2

S_повн.=                       π(R1+R2)L

+π𝑅12+π𝑅22

𝑉 =𝜋𝐻(𝑅₁² +𝑅_`1𝑅₂ +𝑅₂²),

де H – висота зрізаного конуса

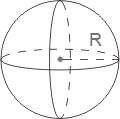
Куля 

(сфера)

Тіло обертання, яке виходить при обертанні круга (кола) навколо діаметра.

Тіло, що складається з усіх точок простору, відстань від яких до даної точки не перевищує заданої. Ця точка – центр кулі.  Радіус – задана відстань. Поверхня кулі називається сферою.

–

Площа бічної поверхні кулі      дорівнює почетвереній             площі великого круга:

S=4πR²=πD²,

де    R    –     радіус     кулі

(сфери),

D – діаметр кулі (сфери)

Об'єм кулі      дорівнює добутку площі її поверхні на третину радіуса:

𝑉 = 𝑆𝑅

𝑉 = 4πR²𝑅

𝑉 = πR³