Відкритий урок на тему "Прямокутна система координат"

ПЛАН УРОКУ

Дата «___» ___________________ 2021 р.

Предмет: Геометрія

Тема: Декартові координати у просторі

Тема уроку: Прямокутна система координат у просторі. Підготовка до ЗНО.

Мета уроку:

- узагальнити знання учнів про прямокутну систему координат у просторі; закріпити навички обчислення координат середини відрізка, довжини відрізка; показати практичне застосування теми при розв’язуванні задач при підготовці до ЗНО.

- стимулювати активну пізнавальну діяльність; сприяти розвитку її емоційної сфери, збудити інтерес до самостійного вирішення проблем; розвивати навички самостійної діяльності.

- формувати соціальну компетентність, розвивати свідому трудову дисципліну, виховувати впевненість у своїх можливостях, прищеплювати учням віру у власні сили і розум.

Тип уроку: Урок практичного застосування знань та вмінь.

Вид уроку: Змішаний.

Форма організації навчальної діяльності колективна,індивідуальна.

Методи: Словесні,наочні,практичні,інтерактивні,частково-пошукові,метод часових обмежень.

Дидактичне забезпечення: Презентація викладача, тести.

Обладнання: нетбуки, проектор, тестова система «Test-W»

Девіз уроку:

«Те, що ми знаємо — обмежено,

 а те, що ми не знаємо - нескінченно»

 

П.Лаплас

 

Хід уроку.

І. Організаційний момент.

Добрий день. Сьогодні я бажаю вам бути

Уважними

Сміливими

Працелюбними

Ініціативними

Хоробрими

Тобто, одним словом, - успіху!

ІІ. Актуалізація опорних знань.

1. «Те, що ми знаємо — обмежено, а те, що ми не знаємо - нескінченно»,— стверджував П’єр Лаплас (французький математик). Сьогодні ми продовжуємо знайомство з безмежною прямокутною системою координат у просторі.

То ж зараз за допомогою інтерактивної вправи «Мікрофон» (Викладач-учень), згадаємо, що нам відомо про прямокутну систему координат.

Тож почнемо:

• Чому прямокутну система координат називають ще декартовою?

(Декартову систему координат на площині вперше запропонував відомий французький математик Рене Декарт близько 1637 року в праці «Геометрія»)

• Як виглядає система координат у просторі?

(Через довільну т. О проведено три попарно перпендикулярні прямі x, y, z. На кожній з них вибрано напрям, позначений стрілками, та одиничний відрізок)

• Яку назву мають координатні прямі у просторі?

(вісь абсцис, вісь ординат, вісь аплікат)

• Чому дорівнюють координати точки О початку координат?

(0;0;0)

• Якщо вибрати в просторі будь-яку точку, то скільки чисел ставиться їй у відповідність? Як вони називаються?

(3 числа, абсциса, ордината, апліката)

2. Виконуючи вправу «Мікрофон», ми повторили загальні відомості про прямокутну систему координат у просторі.

Добре, але крім них нам сьогодні потрібно пригадати ще основні формули, а саме координати середини відрізка і відстань між двома точками.

Пропоную інтерактивну вправу «Знайди помилки у формулах»

Записані формули з помилками. Завдання: знайти помилки і виправити їх, а потім сказати що можна знайти за їх допомогою.

т. М (х_м;y_м;z_м) – середина відрізка АВ, А(x_а;y_а; z_а), В(x_в;y_в;z_в)

x_м=     y_м=    z_{а =        (}z_{м = )}

Відстань між двома точками А(x_а;y_а; z_а) і В(x_в;y_в;z_в) простору знаходиться за формулою

АВ =

lll. Повідомлення теми, мети. Мотивація навчальної діяльності.

Як Ви знаєте, немає теорії без практики , тому темою нашого уроку є «Прямокутна система координат у просторі. Підготовка до ЗНО».

Мета уроку:

• закріпити навички обчислення координат середини відрізка, довжини відрізка;
• показати практичне застосування теми  при розв’язуванні задач під час підготовки до ЗНО.

lV. Практичне закріплення умінь та навичок учнів. (розв’язування задач)

Викладач: Сьогодні на уроці я пропоную вам розв’язувати задачі взяті з завдань ЗНО минулих років.

 

 

Завдання 1.(ЗНО 2016)(усна форма роботи)

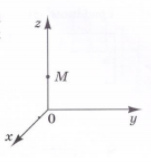
У прямокутній декартовій системі координат у просторі на осі z вибрано точку М (див. рисунок). Серед наведених варіантів укажіть можливі координати цієї точки.

А	Б	В	Г	Д
(1;0;0)	(1;1;0)	(0;0;1)	(0;0;-1)	(0;1;0)

 

Відповідь: В

Завдання 2. (ЗНО 2012 І сесія) (усна форма роботи)

Яка з наведених точок належить осі Оz прямокутної системи координат у просторі?

А	Б	В	Г	Д
М(0;-3;0)	N(3;0;-3)	K(-3;0;0)	L(-3;3;0)	F(0;0;-3)

Відповідь: Д

Завдання3. (ЗНО 2012 ІІ сесія) (усна форма роботи)

Яка з наведених точок лежить у площині Оxz прямокутної системи координат у просторі?

А	Б	В	Г	Д
(0;-3;0)	(0;4;-3)	(3;0;-4)	(-4;3;0)	(-3;3;3)

Відповідь: В

Завдання 4.(ЗНО 2010 ІІ сесія) (самостійно з подальшою перевіркою)

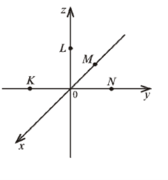
На рисунку зображено прямокутну систему координат у просторі, на осях якої позначено точки K, L, M, N. Установіть відповідність між точками K, L, M, N (1-4) та їх можливими координатами (А-Д).

Точка	Координати точки
1 K	А  (-3;0;0)
2 L	Б(0;-3;0)
3 M	В  (0;0;-3)
4 N	Г  (0;0;3)
	Д  (0;3;0)

Відповідь: 

	А	Б	В	Г	Д
1		×
2				×
3	×
4					×

 

Завдання 5. (ЗНО 2015 основна сесія)(самостійно з подальшою перевіркою)

У прямокутній декартовій системі координат у просторі xyz задано точки А(2;0;0) і В (-4;2;6). До кожного початку речення (1-4) доберіть його закінчення (А-Д) так, щоб утворилося правильне твердження.

Початок речення		Закінчення речення
1	Середина відрізка АВ є точка	А	(-1;1;3)
2	Проекція точки В на вісь z є точка	Б	(0;2;0)
3	Проекція точки В на площину xz є точка	В	(-4;0;6)
4	Проекцією точки В на вісь y є точка	Г	(0;0;6)
		Д	(-2;2;6)

Відповідь:

 

	А	Б	В	Г	Д
1	×
2				×
3			×
4		×

 

Завдання 6(на дошці).

Точки М(-2; 3; 4), N(3; 5; 2) і К(3; -5; 1) — середини сторін трикутника. Знайдіть координати вершин цього трикутника.

Відповідь: А(-2;-7;3), В(-2;13;5), С(8;-3;-1)

Додаткове завдання.(самостійно з подальшою взаємоперевіркою (робота в парах)).

Знайдіть довжину медіани AM трикутника АВС, якщо А (2; 1; 3), В(2; 1; 5), С(0; 1; 1).

Розв’язання

1. Знайти координати точки М.

2. Знайти довжину відрізку AM.

Відповідь: М(1;1;3), АМ=1

 

V. Самостійне виконання учнями практичних завдань на нетбуках (Test-W)

Якщо ви хочете навчитись плавати, то сміливо заходьте в воду, а якщо хочете навчитися розв’язувати задачі, то розв’язуйте їх. (Слова видатного американського математика Дьорда Пойа).

Тест

1. Під яким кутом перетинаються координатні прямі у просторі?

А	Б	В	Г	Д
Гострий	Прямий	Тупий	Розгорнутий	Інша відповідь

 

2. Як називають вісь Оу?

А	Б	В	Г	Д
Ордината	Абсциса	Апліката	Бісектриса	Інша відповідь

3. Як називають вісь Оz?

А	Б	В	Г	Д
Ордината	Абсциса	Апліката	Бісектриса	Інша відповідь

 

4. Якщо точка належить осі Ох, то її координати:

А	Б	В	Г	Д
(0; у; 0)	(x; у; 0)	(0; у; z)	(х; 0; 0)	Інша відповідь

 

5. Якщо точка належить площині хz, то її координати:

А	Б	В	Г	Д
(0; 0; z)	(x; у; 0)	(х; 0; z)	(х; 0; 0)	Інша відповідь

 

6. Якщо точка належить осі Oy, то її координати:

А	Б	В	Г	Д
(x;y;z)	(x;0;z)	(0;y;0)	(0;0;z)	Інша відповідь

 

7. Якщо точка належить площині yz, то її координати:

 

А	Б	В	Г	Д
(0;y;z)	(x;0;z)	(x;y;0)	(x;0;0)	Інша відповідь

 

8. Відстань між точками у просторі обчислюється за формулою:

А	Б	В	Г	Д
	xв-xа		xа-xв	Інша відповідь

 

9. Які координати середини С відрізка АВ, якщо А (0;2;11), В (2;0; -1)?

А	Б	В	Г	Д
(1;1;10)	(1;0;5)	Інша відповідь	(-1;1;5)	(1;1;5)

 

10. Знайти відстань від точки А (-1;2;-2) до початку координат О (0;0;0)

А	Б	В	Г	Д
9	3	1	Інша відповідь	5

 

11. Знайти довжину відрізка АВ, якщо А(-1;3;-1) і В(-1;0;-5)

А	Б	В	Г	Д
9	3	10	Інша відповідь	5

 

12.  Знайдіть на осі x точки, які відділені від точки А(4;-2;3) на відстань 7

А	Б	В	Г	Д
(4;0;0)	(10;0;0)	(11;5;10)	(-2;0;0)	(-2;-9;-4)

 

Відповіді до тесту:

1	2	3	4	5	6	7	8	9	10	11	12
Б	А	В	Г	В	В	А	А	Д	Б	Д	Б,Г

 

VІ. Підсумок уроку.

Повертаючись до девізу уроку, можна сказати, що нескінченність зменшується з кожним уроком.

Рефлексія.

Сьогодні на уроці я

дізнався...

зрозумів...

навчався...

найбільший мій успіх – це...

на наступному уроці я хочу...

VIІ. Домашнє завдання

Опрацювати §11

Розв’язати

І рівень

Задача 1.

Знайдіть на осі x точки, які відділені від точки А(4;-2;3) на відстань 7

ІІ рівень

Задача 2.

Дано вершини трикутника АВС: А(-2; 0; 1), В(8; -4; 9), С(-1; 2; 3). Знайти довжину медіани трикутника, проведеної із вершини С.

ІІІ рівень

Задача 3.

Точки М(-4; 5; 6), N(5; 7; 4) і К(5; -7; 2) — середини сторін трикутника. Знайдіть координати вершин цього трикутника.