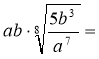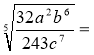Опорний конспект "Найпростіші перетворення радикалів"

№2

  а)  _____________________________          Відповідь:  _______

  б) ____________________________          Відповідь:  _______

  в) ___________________________          Відповідь:  _______

  г)                                                                    Відповідь:  _______

  д) _________________________           Відповідь:  _______

3.  Зведення радикалів до найпростішого вигляду

  Корінь зведений до найпростішого вигляду, коли:

1. підкореневий вираз не містить дробів;
2. раціональні множники винесені за знак кореня;
3. показник кореня і показник степеня скорочені на їхній найбільший спільний дільник.

№3

   Звести радикали до найпростішого вигляду:

   а)                                                                               Відповідь:  _______

   б) ____________________________         Відповідь:  _______

 4.  Подібні радикали

Радикали називаються  подібними, якщо після зведення їх до найпростішого вигляду  вони  мають ___________________________

  ___________________________________________________

                                Наприклад:  ____________________________________________________

      №4

    Довести подібність радикалів:      і   .

   Доведення:

 __________________________________________

 __________________________________________

Найпростіші перетворення радикалів

  1.  Винесення множника з-під знака радикала

     В деяких випадках підкореневий вираз розкладається на множники так, що із одного чи декількох із них можна добути точний корінь. Добувши корені із цих множників, одержані числа можна записати перед знаком кореня. Таке перетворення називають винесенням множника за знак радикала.

  !  При винесенні буквених множників за знак кореня під всіма буквами слід  розуміти  лише невід’ємні числа.

     Наприклад:   1) ;

                            2) .

  (ІІ спосіб: досить показник степеня множника, що стоїть під коренем, поділити на показник степеня кореня: частка покаже, в якому степені цей множник буде стояти перед коренем, а остача – в якому степені цей множник залишиться під знаком кореня.)

№1

  а)  ______________________________             Відповідь:  _______

  б) ______________________________            Відповідь:  _______

  в)____________________________              Відповідь:  _______

  г)                                                                    Відповідь:  _______

 2.  Внесення множника під знак кореня

     Перетворення, обернене до винесення множників з-під знака кореня, називається  внесенням множника під знак кореня.

  !  Щоб внести множник під знак кореня, необхідно піднести його до степеня, показник якого дорівнює показнику кореня, і записати результат під знаком кореня.

       Наприклад:   ;

 !          Під знак кореня можна вносити як числові, так і буквені множники, тільки необхідно пам’ятати, що буквений множник не може бути від’ємним. 

  !  Раціональний множник, що стоїть перед знаком кореня, називають _____________________.

Порівняння радикалів

             Теорема:  якщо , то , тобто більшому додатному підкореневому виразу відповідає і більше значення кореня.

      №5

    Порівняйте числа:         і  .

Розв’язання:

     ___________________________________

    _______________________________

   _______________________________

   ______________________________________________________

                  Відповідь:   _________________

Домашнє завдання:

• вивчити теорію;
• розв’язати приклади (записані впродовж уроку);
• розташувати в порядку зростання:    ,   , 

Розв’язання:

    _____________________________________________________

   ______________________________________________________

   ______________________________________________________

   ______________________________________________________

                   Відповідь:   ______________________