Основна властивість дробу. Зведення дробів до нового знаменника

Тема. Основна властивість дробу. Зведення дробів до нового знаменника

Мета: домогтися засвоєння учнями змісту основної властивості раціонального дробу (у двох варіантах) та схеми її доведення, змісту поняття «скоротити раціональний дріб» та алгоритму скорочення раціонального дробу, а також правила знаків для раціональних дробів; сформувати вміння відтворювати названі властивості й використову­вати ці властивості та алгоритми для розв'язування вправ.

Тип уроку: засвоєння знань та вмінь, відпрацювання навичок.

Наочність та обладнання: опорний конспект «Основна властивість дробу».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

1) Розв'язування вправ домашнього завдання у формі самопере­вірки за зразком.

2) Сильні учні під час перевірки виконують індивідуальні завдання.

Картка 1

1. Виконайте скорочення дробів: а) 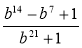; б) .
2. Доведіть тотожність а⁴ + а² + 1 = (а² + а + 1) (а² – а + 1).

Картка 2

1. Виконайте скорочення дробів: а) 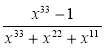; б) .
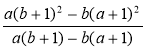2. Доведіть тотожність b⁸ + b⁴ + 1 = (b⁴ + b² + 1)(b⁴ – b² + 1).

III. Формулювання мети і завдань уроку

Мета уроку стає цілком зрозумілою після роботи з матеріалом по­переднього уроку (див. урок 3), в ході якого було зроблено акцент на тому, що основна властивість дробу може мати дні форми запису. Як­що одна з них є записом у буквеному вигляді правила скорочення дробів, то інша не була вивчена на попередньому уроці. Усвідомлення цього факту дає можливість сформулювати мету уроку – вивчення змісту дії з раціональними дробами,   що  виражається  формулою , складання алгоритму виконання цієї дії, а також формування вмінь застосовувати складений алгоритм на практиці.

IV. Актуалізація опорних знань та вмінь

 З метою успішної роботи учнів із навчальним матеріалом уроку слід попередньо розв'язати усні вправи, що передбачають по­вторення алгоритмів виконання зведення звичайних дробів до нового знаменника, різних способів розкладання цілих виразів на лінійні множники, а також на повторення алгоритмів, вив­чених на попередніх уроках.

Виконання усних вправ

1. Скоротіть дроби: ; ; ; .
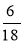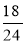2. Зведіть дріб до знаменника 48; ; ; ; ; ; .
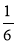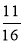3. Подайте число 5 у вигляді дробу зі знаменником: 2; 5; 1; 10; п.
4. Подайте вирази у вигляді добутку: 5х + 10у; х² – 16; 22у² – 11у;

у⁵ – у⁷; 5х – 15; 16х – 2ху; 8 + y³; 3y² – 3y⁴.

5. Знайдіть пропущені числа (щоб рівності були правильними):

а) 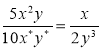 ; б) .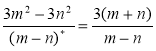

V. Засвоєння знань

План вивчення нового матеріалу

1. Основна властивість дробу для зведення (раціональних) дробів до нового знаменника.
2. Алгоритм зведення раціонального дробу до нового знаменника.
3. Приклади застосування алгоритму.

 Вивчення матеріалу уроку починається із формулювання пра­вила зведення (з використанням опорного конспекту 2) раціо­нального дробу до нового знаменника у формах словесній та тотожності , яка доводиться з допомогою тих самих властивостей, що були використані на попередньому уроці під час доведення правила скорочення раціональних дробів (див. урок 3).

Далі виконується робота зі складання алгоритму (орієнтовної схе­ми дій) при зведенні раціонального дробу до нового знаменника. Під час складання алгоритму слід зробити акцент на таких моментах:

• Так само як і в разі зведення звичайних дробів, під час зведення раціональних дробів до нового знаменника слід розуміти, що зведен­ня можливе лише у випадку, якщо новий знаменник «ділиться» на старий (у випадку раціональних дробів це означає, що розклад «нового» знаменника на множники має містити всі множники, які є в розкладі на множники «старого» знаменника);
• так само як і в разі зведення звичайних дробів, під час зведення раціональних дробів до нового знаменника слід спочатку знайти до­датковий множник для даного дробу;
• на відміну від випадку зведення звичайних дробів до нового знамен­ника під час зведення до нового знаменника раціонального дробу додатковий множник зазвичай знаходять не діленням знаменників, а розклавши знаменники (новий і старий) на множники та порівняв­ши здобуті розклади (у випадку якщо знаменники є одночленами, можна виконати ділення нового знаменника на старий, записавши частку у вигляді дробу та скоротити її).

Зрозуміло, що усвідомленому сприйняттю учнями всіх сформульо­ваних положень сприятиме демонстрація достатньої кількості при­кладів застосування складеного алгоритму.

VI. Формування вмінь

Виконання усних вправ

1. Назвіть чисельник і знаменник раціонального дробу:

а) ; б) ; в) ; г) .

Які з поданих дробів можна звести до знаменника:

2а²b³; 6а³b²; 9a³b⁴; 2(a – b); (a – b)(a + b); (х + у)²; (х + у)(а – b)?

2. Заповніть пропуски так, щоб рівності були правильними:

а) ; б) ; в) ;

 г) .

3. Знайдіть додатковий множник для зведення дробу:

а) до знаменника b²;  б) до знаменника 4ху;

в) до знаменника 10 – а; г) до знаменника а² – 100.

Виконання письмових вправ

 Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту.

1. Розкладання многочленів на множники.

1) Розкладіть на множники:

а) a²b + ab²; б) х³у – ху³; в) 7x² – 14ху + 21ах; г) 9ху – 3bу + 15ау;

д) х⁴ – х³ + х² – х; є) с⁴ – 2с³ – с² + 2с; ж) (а – 2)² – 25а²; з) (b + 3)² – 36b²;

и) 125x³ + 8; к) 216х³ – 27; л) (a + 1)³ + а³; м) (b + 2)³ – 8b³.

2. Запис цілого виразу у вигляді дробу з поданим знаменником.

1) Подайте вираз 2а + b у вигляді дробу зі знаменником, що до­рівнює:

а) b; б) 5; в) 3а; г) 2а – b.

3. Зведення дробу до заданого знаменника (який вже розкладено на множники і такого, який потребує попереднього розкладання на множники).

1)  Зведіть дроби: ; ; ; до знаменника 24а³b².

2)  Зведіть дріб:

а) до знаменника (а – b)²; б) до знаменника х² – а²;

в) до знаменника x³ – 1; г) до знаменника а³ – b³;

д) до знаменника b – y; e) до знаменника 10 – а;

ж) до знаменника 4 – р²; з) до знаменника 2(а² – 9).

3)  Зведіть дріб:

а) до знаменника х² + ху; б) до знаменника х² + 2ху + у²;

в) до знаменника а² – b²; г) до знаменника т³ – п³.

4. Перевірити, чи можна поданий раціональний дріб звести доданого знаменника, і якщо це можливо, то виконати зведення до цього знаменника.
5. Виконання вправ на повторення: скорочення дробів (знайти зна­чення дробу, попередньо скоротивши його; доведення тотожнос­тей, складених із двох раціональних дробів), а також на повторення алгоритму знаходження ОДЗ дробового виразу.

1)  Скоротіть дріб:

а) ; б) ; в) .

2)  Знайдіть значення дробу:

а) при а = -2, b = -0,1; б) при с = , d = ;

в) 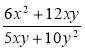при х = , у = -0,4; г) при х = -0,2, у = -0,6.

6. Виконання логічних вправ та завдань підвищеного рівня складності.

1)  Скоротіть дріб (п — натуральне число):

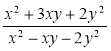а) ; б) ; в) ; г) .

2) Доведіть тотожність:

а) ; б) .

3) Знайдіть пропущений вираз:

З метою попередження типових помилок із самого початку слід звертати увагу учнів на те, що під час запису добутку чисельника та знаменника раціонального дробу на додатковий множник слід викону­вати правила запису добутку многочлена на одночлен і многочлена на многочлен (тобто многочлен, що є множником, записувати в дужках).

VII. Підсумки уроку

Чи правильно виконано зведення дробів до нового знаменника? Якщо ні - виправте помилку.

; ; .

VIII. Домашнє завдання

1. Повторити формулювання основної властивості дробу, її записи для випадку скорочення дробів та для випадку зведення дробів до нового знаменника.
2. Виконати вправи, що передбачають: зведення дробів до нового зна­менника; скорочення дробів.
3. На повторення: вправи на знаходження ОДЗ дробових виразів та використання умови рівності дробу нулю (підготуватись до само­стійної роботи з теми «Дроби. Основна властивість дробу».