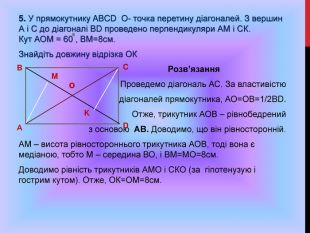
Особливості розв'язування геометричних задач.
Про матеріал
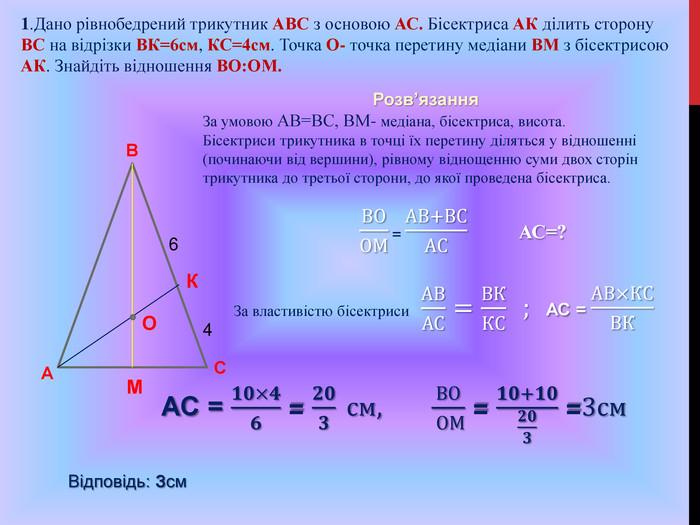
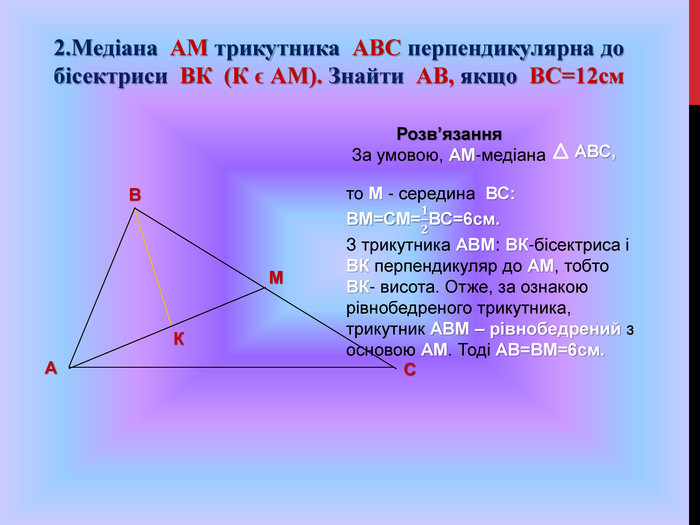
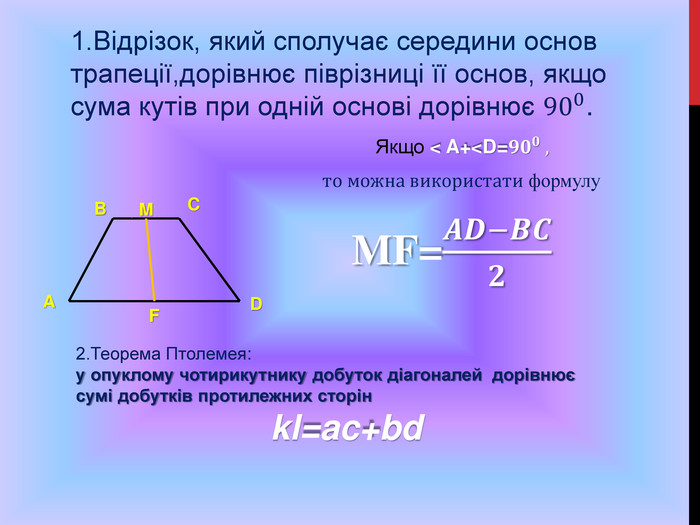
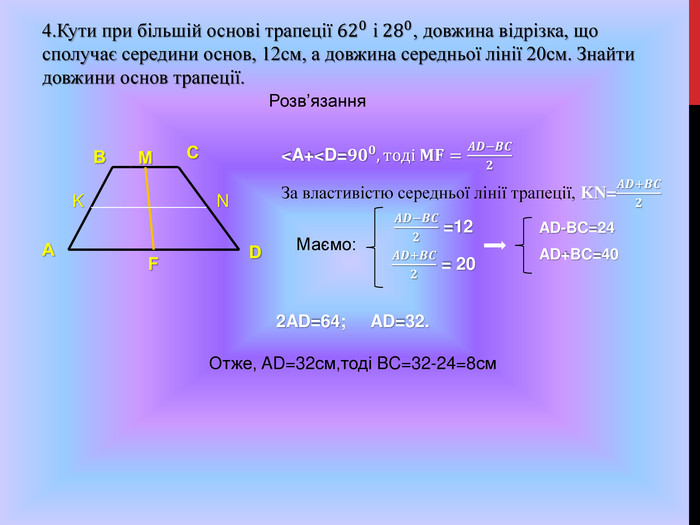
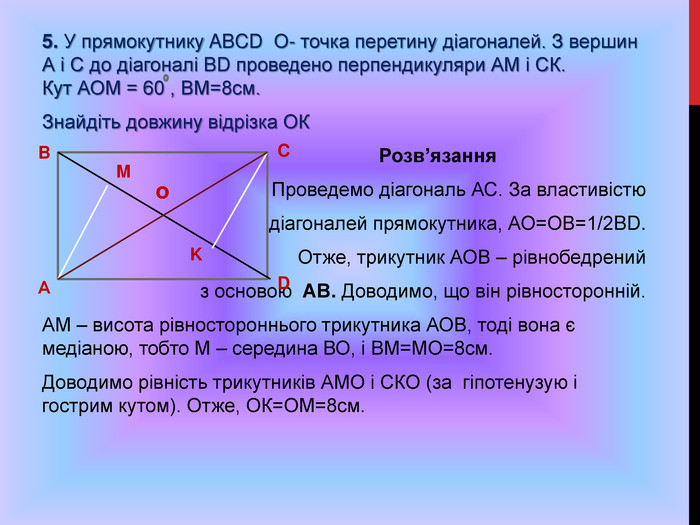
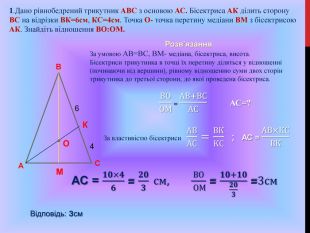
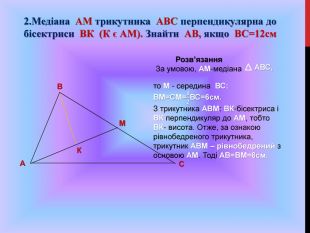
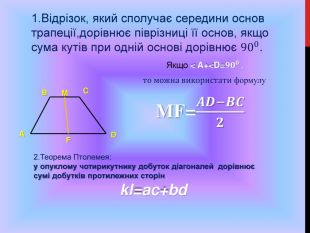
Підготовка до ЗНО. Особливості розв'язування геометричних задач. Дуже часто ми стикаємося з задачами, для розв'язування яких потрібно використовувати формули, які не часто використовуються на уроках математики.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку