Методичний матеріал:"Інтерактивні методи навчання математики".

Інтерактивні методи навчання математики

«Інтерактивний» означає здатний до взаємодії, до діалогу. Інтерактивне навчання – це діалогове навчання. Поповнення знання відбувається лиш під час взаємодії вчителя та учнів між собою і має конкретну прогнозовану мету. Це – створення таких умов навчання. За яких кожен учень відчуває свою успішність, інтелектуальні досягнення, що робить продуктивним сам процес набуття знань.

Особливість інтерактивну в тому, що в ході навчання:

1. всі учні задіяні в процесі пізнання, мають можливість аналізувати те, що вони знають, розуміють і думають з цього приводу;
2. виключається як домінування одного учасника над іншим, так і домінування однієї думки над іншими;
3. відбувається позитивне діалогове спілкування.

В процесі такого спілкування учні набувають умінь критично мислити, зважувати всі думки, приймати рішення, дискутувати.

Інтерактивне навчання дозволяє різко збільшити процент засвоєння матеріалу, тому що впливає не тільки на свідомість учня, ф й на його почуття, волю. Як засвоюється матеріал розглянемо на «Піраміді навчання».

Лекція – 5% засвоєння

Читання – 10 % засвоєння

Відео/аудіо матеріали – 20% засвоєння

 Демонстрація – 30% засвоєння 

 Дискусійні групи – 50% засвоєння  

      Практика через дію – 75% засвоєння     

   Навчання інших – 90% засвоєння  

Як бачимо з піраміди тільки через дію, через навчання інших відбувається високий відсоток засвоєння знань.

Інтерактивне навчання має як сильні, так і слабкі сторони.

Слабкі сторони: для вивчення невеликого обсягу інформації витрачається багато часу, може виникнути необхідність корекції знань, умінь, навичок.

Сильні сторони: розширюється пізнавальні можливості учнів; учні можуть переносити отриманні знання, вміння, навички на різні предмети та позашкільне життя; високий відсоток засвоєння знань; забезпечуються демократичні, рівноправні відносини між вчителям і учнем та між учнями; розвиваються комунікативні навички учнів; проявляється інтерес до навчання.

Будь-яка педагогічна технологія повинна відповідати основним критеріям:

•         системності;
•         керованості;
•         ефективності4
•         відтворюваності.

Тому виходячи із вище сказаного, вважають, що інтерактивна модель навчально-виховного процесу, передбачає використання інтерактивних технологій за різних форм організації навчання.

О.Пометун розділяє технології на чотири групи залежно від мети уроку та форм організації навчальної діяльності учнів:

1. Інтерактивні технології кооперативного навчання.
2. Інтерактивні технології колективно-групового навчання.
3. Технології ситуативного моделювання.
4. Технології опрацювання дискусійних питань.

До першої групи відноситься:

• робота в парах (один проти одного, один-вдвох-всі разом);
• два-чотири-всі разом;
• карусель:
• робота в малих групах.

Залежно від змісту та мети навчання можливі різні варіанти організації роботи груп. Це може бути «Діалог», «Синтез думок», «Спільний проект», «Пошук інформації», «Коло ідей», «Акваріум».

До другої групи відносяться технології, що передбачають одночасно спільну (фронтальну) роботу всього класу. Це може бути «Мікрофон», «Незакінчені речення», «Мозковий штурм»,

Навчаючи –учусь», «Ажурна пилка», «Дерево рішень».

До технології ситуативного моделювання (ігрове моделювання явищ, що вивчаються) відносяться: симуляції або імітації гри, громадські слухання, розігрування ситуації за ролями.

До четвертої групи відноситься: «Метод ПРЕС», «Займи позицію», «Зміни позицію», «Неперервна шкала думок», «Дискусія», «Дебати».

Чому інтерактивний урок?

На уроках учні найчастіше пасивні, у них відсутній інтерес до навчання, знижена якість знань, перевантаження домашніми уроками і все це шкідливо впливає на здоров’я. І щоб подолати всі ці проблеми потрібно використовувати інноваційні технології, зокрема технології інтерактивного навчання.

Структура інтерактивного уроку:

1.                    мотивація;
2.                    оголошення теми та очікуваних результатів;
3.                    надання необхідної інформації;
4.                    інтерактивна вправа – центральна частина заняття;
5.                    підведення підсумків, оцінювання результатів уроку.

Технології кооперативного навчання

Два – чотири – всі разом.

Виділимо чотири типологічні групи учнів, як вивчають математику.

Група А.

Учні мають глибоку, повні, міцні знання основних фактів за вивчений курс навчання, знають означення основних понять, їх позначення. Вміють пояснювати, аргументувати, доводити, узагальнювати математичні факти, виділяти суттєве у вивченому матеріалі. Знають методи, способи, правила, алгоритми розв’язування задач. Вміють наводити свої приклади.

Група Б.

Учні мають міцні знання основних фактів, які входять у зміст навчання математики, але не завжди можуть аргументувати, доводити, узагальнювати, наводити свої приклади. Знають основні методи розв’язування задач, але важче їм розв’язувати задачі, які потребують творчого пошуку, діяльності в новій ситуації. Тому, під час розв’язання задач, таким учням потрібна допомога вчителя.

Група С.

Учні володіють мінімумом знань, умінь, навичок, яких достатньо для застосування за зразком. Вміють відповідати на питання без доведень і міркувань. Можуть розв’язувати стандартні задачі.

Група Д.

Учні погано розуміють факти, поняття, правила, способи розв’язування задач. Не можуть повторити означення, приклади, текст із підручника або вчителя, не завжди розуміють зміст математичних рішень, умови задачі. Не вміють застосовувати відомі правила без допомоги вчителя або розв’язувати задачі за зразком.

Типологічні групи – це групи для вчителя. На їх основі в класі створюються робочі групи, які дозволяють вчителю здійснити диференціальний підхід і надати групі своєчасну допомогу.

Склад групи комплектується із учнів різних типологічних груп. При  формуванні груп по два може бути три способи.

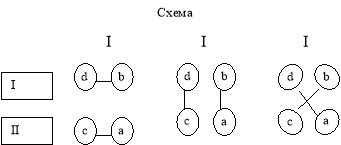
При формуванні груп необхідно враховувати інтереси учнів до предмету, поведінку, відносини один з одним, мотиви навчання, зібраність. Не потрібно включати в одну групу 2-х недисциплінованих учнів.

Якщо група з 3-х чи 4-х учнів, то одного з учнів необхідно назначити асистентом. Він спостерігає за роботою групи, розподіляє завдання між учнями, допомагає своїм товаришам.

Наприклад.

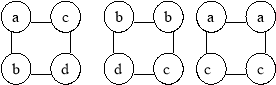
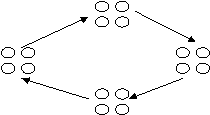
Карусель

Геометрія. 8 клас.

Тема. Властивості чотирикутників.

Утворюємо групи по 4 учні в кожній за кольором розданих вчителем карток.Кожній групі дається аркуш паперу і кольорові олівці такого ж кольору, як їх картки.

Завдання групам. Записати означення і властивості зображеної фігури.

1 група – паралелограм.   2 група – прямокутник.

3 група – ромб.     4 група – квадрат.

За 2-3 хвилини накреслити і записати схематично на аркуші означення цього чотирикутника.

Передати аркуш наступній групі за годинниковою стрілкою, а на отриманому аркуші написати схематично властивість фігури, яка накреслена на ньому.

Коли свій аркуш повернеться до групи, учні повинні перевірити всі записи і, можливо, доповнити його і підготуватися до виступу.

Доповідач від кожної групи розповідає про властивості чотирикутника, висловлює основні моменти доведення властивостей.