Означення квадратного рівняння. Неповні квадратні рівняння.

 

Тема. Означення квадратного рівняння. Неповні квадратні рівняння.

Мета: ( освітня):

-домогтися свідомого розуміння означення квадратного рівняння;  зведеного квадратного рівняння та неповного квадратного рівняння; - засвоїти назви коефіцієнтів квадратного рівняння;

-сформувати вміння визначати коефіцієнти квадратного рівняння та за ними робити висновок про  вид квадратного рівняння;

-формувати вміння розв’язувати неповні квадратні ;

(виховна): виховувати в учнів культуру математичних записів , культуру спілкування та культуру поведінки, сприяти розвитку всесторонньо розвинутої особистості, вихованню етичних норм, довіру до товаришів.

(розвиваюча): розвивати в учнів уважність, розвивати мислення, увагу, пам’ять ,спостережливість, вміння аналізувати та виділяти головне.

Учні повинні :

• розпізнавати квадратні рівняння серед інших рівнянь;
• визначати коефіцієнти в квадратному рівнянні;
• знати означення квадратного рівняння ;неповного квадратного рівняння та зведеного квадратного рівняння.
•  уміти розв’язувати неповні квадратні рівняння.

 

Обладнання: дошка,  комп’ютер, підручник для 8 класу, мультимедійна дошка, картки оцінювання

Тип уроку. Урок засвоєння нових знань.

 

                                      Хід уроку

І.Організаційний момент

 Перевірка наявності учнів в класі та їх готовності до уроку.

ІІ. Вступне слово вчителя (доцільно проводити з метою формування комунікативних компетентностей)

Рівняння – це не просто рівність,
З однією змінною чи кількома.
Рівняння – це думок активність,
Це інтелекту боротьба.

ІІІ. Актуалізація знань.

Слайд 2 « Розв`яжіть кросворд»

1.Рівність ,що містить невідоме ( рівняння);

2.Значення змінної, що перетворює рівняння на правильну рівність дев'ять корінь);

3.Рівняння,що мають однакові корені або не мають їх ( рівносильні);

4.Число,яке стоїть перед змінною у рівнянні ( коефіцієнт);

5.Рівняння виду ах=в, де х- змінна, а і в-  деяки числа ( лінійне);

6.Добуток коренів кожного з рівнянь 2х=3; 5х=7 ;5х=0( нуль)

7.Кількість коренів рівняння 0х=9 ( жодного).

ІV.. Мотивація вивчення теми.

Слайд 3

Проблемна задача.

Одне з двох чисел більше від другого на 2, а їх добуток дорівнює 35. Знайти ці числа.

 Розв’язання:

    Позначимо менше число через х. Тоді більше число буде дорівнювати х+2. Їх добуток 35. Маємо рівняння:

х(х+2)=35:

х² + 2х - 35=0.

Це - рівняння другого степеня з однією зміною.

Такі рівняння називаються квадратними. Ознайомлення учнів з темою, яку учні будуть вивчати та з вимогами до знань і вмінь.

 

Слайд 4

ІІІ.Повідомлення теми, мети та завдань уроку.

 

Слайд 5

Квадратним називають рівняння виду

                             ах²+вх+с=0,

де х - змінна, а а, в, с – дані числа, причому а ≠ 0.

Слайд 6

 Інтерактивна вправа- анаграма ( cтворена в програмі smart)

« А ну ж бо відгадай! »

Слайд 7-8

Історична довідка  . Квадратні рівняння вміли розв’язувати вавілоняни близько 2000 років до н. е. відомо, що їхні методи розв’язання майже збігаються із сучасними. Проте невідомо, яким чином вавилоняни дійшли до цих методів: майже на всіх знайдених до того часу клинописних текстах збереглися лиш вказівки до знаходження коренів рівнянь і немає ані найменшої згадки про від’ємні числа і про загальні методи розв’язування рівнянь. В стародавній Греції квадратні рівняння розв’язувалися за допомогою геометричних побудов. Методи, які не пов’язувалися з геометрією, вперше наводить Діафант Александрійський у ІІІст.  У своїх книгах “Арифметика” він наводить приклади розв’язування неповних квадратних рівнянь. Його книги з описом способів розв’язування повних квадратних рівнянь до нашого часу не збереглися. Загальне правило розв’язування квадратних рівнянь було сформульоване німецьким математиком М. Штіфелем (1487 – 1567). Виводом формули загального розв’язку квадратних рівнянь займався Франсуа Вієт. Він же й вивів формули залежності коренів рівняння від коефіцієнтів у 1591 році. Після праць нідерландського математика А. Жираре (1595 – 1632), а також Декарта і Ньютона спосіб розв’язання квадратних рівнянь набув сучасного вигляду.

 ІV. Сприйняття й усвідомлення поняття повного та неповного квадратного рівнянь.

Слайд 5

Означення квадратного рівняння:

Квадратним називають рівняння виду

                             ах²+вх+с=0,

де х - змінна, а а, в, с – дані числа, причому а ≠ 0. Числа a, b, c  - називаються   коефіцієнтами квадратного  рівняння

 а – перший коефіцієнт;

b – другий коефіцієнт;

с – вільний член.

         Слайд 13.

Усні вправи.  Яке з даних рівнянь квадратне:

         а) 5х²-3х+2=0;   б)6х-7=0;   в) (2х-5)² -7=0;  г) 2х-3-х²=0; д) -5х3-x²=2х=0   ,є)(4х-5)x=0

 

         Слайд 14.

Інтерактивна вправа «Визначте коефіцієнти квадратного рівняння».

Слайд 15

Завдання      

    Уважно розглянувши   структуру рівнянь дайте означення зведеного і незведеного квадратних рівнянь  

 

 

 

 

                                                                        

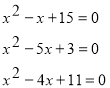
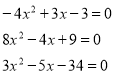
Слайд 16

Квадратне рівняння називається з в е д е н и м ,

 якщо його перший коефіцієнт дорівнює одиниці (а = 1)

 

 

Слайд 17

Перетворіть дане квадратне рівняння у зведене

 

 

 

 

 

 

 

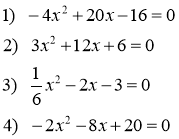
Слайд 18

Робота в групах .

Завданням групам:

Розподіліть дані рівняння на чотири групи. Поясніть свій вибір.

 

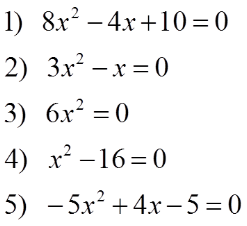
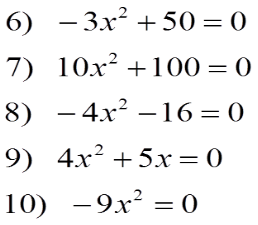
Слайд 19

Робота з випереджальним домашнім завданням ( доцільно проводити з метою формування компетентностей саморозвитку і самоосвіти).

 Учнів класу було поділено на чотири групи. Кожна група отримала своє завдання.

Повідомлення учнів.

І група. Означення повного квадратного рівняння. Види неповних квадратних рівнянь.

Якщо у   квадратному рівнянні                                                                                                                                  а ≠ 0,  в ≠ 0,   с ≠ 0,то воно називається повним квадратним рівнянням.

Наприклад

2х²+5х-7=0

6х+х²-3=0

х²-8х-7=0

25-10х+х²=0.

ІІ група. Означення неповного квадратного рівняння. Види неповних квадратних рівнянь

Якщо у квадратному рівнянні хоча б один із коефіцієнтів  в або с   дорівнює нулю     (b = 0,  c = 0), то таке рівняння називається  неповним квадратним рівнянням

Наприклад

3х²-2х=0

2х+х²=0

125+5х²=0

49х²-81=0

 

Слайд 20

Інтерактивна вправа « Посортуй рівняння.

 

Слайд 21

Оздоровча хвилинка «Гімнастика для очей».Відеовправа.

 

 Слайд 22

Які рівняння об'єднані за спільною ознакою?

Яке з рівнянь зайве?

 

 

 

 

 

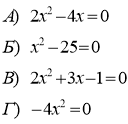
Слайд 23

Розв'яжіть рівняння.

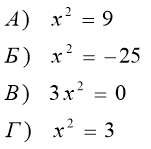Скільки коренів вони мають?

 

 

 

 

 

 

Слайд 24

Усні вправи (ІV група)

Які рівняння об'єднані за спільною ознакою? Яке з рівнянь  зайве?

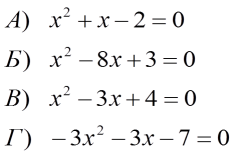
Слайд 25

Завдання групам .

Розв`яжіть рівняння. Встановити, який (які) з коефіцієнтів дорівнюють нулю.  Сформулюйте правило розв`язування   рівняння певного типу.                                          

    Слайд 26

1 група -5х2+15х=0 х2-х=0 4х2+8х=0	2 група Х2-16=0 -2х2-50=0 4х2+16=0
3 група 6х2=0 -4х2=0 х2=0	4 група 4х2=0 -3х2-12=0 х2+2х=0

                                                             

Слайд 27

І група. Рівняння виду ах² = 0.

Якщо а ≠ 0, в = 0, с = 0, то ах² + 0х + 0= 0, тоді

                                     ах² = 0,

                            Розв’язування :

                                    х = 0

                            єдиний корінь.

Завдання.

Розв’язати рівняння

6х² =0,    -4х² =0,      2/5х² =0,

   х=0,         х=0,         х=0.

ІІ.група.Рівняння виду ах² +вх=0

Якщо а ≠ 0, в ≠ 0, с = 0, то

ах² + вх + 0 = 0;

ах² + вх = 0;

х(ах + в) = 0;

х=0  або  ах = -в;

                 х  = - в/а

Завдання.

Розв’язати рівняння

а)4х² +8х=0;              б) -5х² +15х=0;     в)   1/3х²-х=0;

4х(х+2)=0;                 -5 х(х-3)=0;                х(1/3х-1)=0;

4х=0, х+2=0;              -5х=0, х-3=0;            х=0;1/3х=1   

  х=0,  х=-2.                   х=0,  х=3.                 х=0;х=3.

Відповідь: -2; 0           Відповідь:  0; 3           Відповідь:  0; 3.

 

ІІІ група. Рівняння виду ах² + с = 0

Якщо а ≠ 0, в = 0, с ≠ 0, то  ах² + 0х + с=0

                                                ах² +с=0

                                                ах² = - с

                                                х² = - с/а

Якщо - с/а ≥ 0, то                                           Якщо - с/а ˂ 0, то дійсних                                                                                          

                                                                      коренів немає

Завдання.

Розв’язати рівняння

а)4х² +16=0;                  б)-2х² +50=0;                  в)  х²-16=0

4х²= - 16;                        -2х² =-50;                           ( х-4)(х+4)=0

  х² = - 4;                           х² =25;                              х=4; х=-4.

 - 4 <0 ;                                                        

  коренів немає;                       х₁ = -5,      х₂ = 5.  Відповідь: -4; 4.

Відповідь: коренів немає.   Відповідь: -5; 5.                    

V. Відпрацювання навиків розв’язування неповних квадратних рівнянь( доцільно проводити з метою формування продуктивної творчої діяльності)

Слайд 17

Розв’яжіть неповні квадратні рівняння:

а)- 1/9 у²=0;   б)3х² - 4х = 0;  в)4х² - 9 = 0.

 Після розв’язування рівнянь учні здійснюють самоперевірку за розв’язками на  наступному слайді.

Розв’язання

а) - 1/9 у² = 0;             б)12х² - 3х = 0;                     в)9х² - 4 = 0;

       у=0.                    3х(4х-1)=0;                              9х²=4;                  

Відповідь: 0        3х=0 або  4х-1=0;               х²= 4/9;                      

                             х = 0          4х=1;                           х_1  = - 2/3;

                                                 х = 1/4 .                       〖   х〗_2 = 2/3.            

                              Відповідь: 0,   1/4.                 Відповідь: - 2/3;  2/3.

ІVгрупа. Розв’яжіть неповні квадратні рівняння:

4х²=0; -3х²+12=0; х²+2х=0.

Слайд 20

Розв’язання.

а)(х-1)(х-2)=4х;                 б) 3(х+5) – 8 = -5х(х + 2);

 х² - 2х – х +2 = 4х;            3х + 15 – 8 = -5х²  - 10х;

 х² - 2х – х + 2 - 4х = 0;      3х + 15 – 8 + 5х² + 10х = 0;

 х² - 7х + 2 = 0.                   5х²  + 13х + 7 = 0.

V. Відпрацювання навиків розв’язування неповних квадратних рівнянь           ( доцільно проводити з метою формування продуктивної творчої діяльності)

Слайд 28

Інтерактивна вправа «Розв`яжіть рівняння та перевірте відповіді за допомогою чарівного екрану.»

Слайд 29

Розв’яжіть рівняння

 

 

 

 

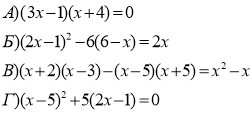
Слайд 30

Тестування ( використання програми MyTest)

1 варіант.

1.Яке з  поданих рівнянь є квадратним?

А)  1-12х=0           Б)  7х²-13х+5=0            В)  48х²+х³-9=0                Г)  = 0

2. В квадратному рівнянні   -3х²+10х+5=0  вказати  старший коеффіциєнт:

А)  10                         Б)  5                      В)  -5                     Г)  -3

3. Розв`язати рівняння : х²+5х=0

А)  коренів немає         Б)  0; 5                          В)  5; -5                   Г)  0; -5

4.Яке з квадратних рівнянь є зведеним:

А)  12-х²+3х=0      Б) х²-7х+16=0      В) -15х²+4х-2=0         Г) 4х²+х-1=0

5.Яке з квадратних рівнянь є неповним:

А) 16х²-9=0         Б)  3-х²+х=0        В)  –х²-х-1=0         Г)  7-7х-7х²=0

6.  Яке з чисел є коренем квадратного рівняння  5х²=0

А)  5         Б)  0           В)  -5              Г)  25

7. Знайдіть добуток коренів рівнянння  2х²-9х=0

А)  немає коренів         Б)  4,5                  В)  -4,5                        Г)  0

8.В якому з квадратних рівнянь вільний член дорівнює нулю:

А)  5х²+2х=0        Б)  х²-9=0     В)  2-х-х²=0         Г)  4х²+5=0

9. Розв`яжіть рівняння :  х²-64=0 

А)  8; -8             Б)  0; 64           В) немає коренів        Г)  8

10. Розв`яжіть рівнянння : 6х-х²=0

А)       немає коренів      Б)  0,-6            В)  6 ;0                Г) 6;-6

2 варіант.

1. Яке з  поданих рівнянь є квадратним?:

А)  = 0         Б)  15х-3=0            В)  6х⁴+х²=0                Г)  4х²+3х-1=0

2) В квадратному  рівнянні   3х²+5х-9=0   вказати вільний член:

А)  9                         Б)  -9                      В)  3                     Г)  5

3.  Розв`язати рівняння :   х²-25=0

А)  0; 25           Б)  немає коренів                  В)  5; -5        Г)  5

4.   Яке з квадратних рівнянь є   незведеним:

А)  х²+3х-5=0      Б)  7х+16+х²=0      В)  12х²+4х-2=0         Г)  х²+х=0

5. Яке з квадратних  рівнянь є зведеним :

А)  16х²-9=0         Б)  3х²+х=0        В)  х²-х-15=0         Г)  -7х²=0

6. Яке з чисел є коренем квадратного рівняння    8х²=0

А)  -8         Б)  8           В)  64              Г)  0

7. Знайдіть добуток коренів рівняння   5х²+12х=0

А)  -2,4          Б)  0                  В)  немає коренів                       Г)  7

8. У якому з даних квадратних рівнянь другий коефіцієнт дорівнює нулю?

А)  х²-9=0         Б)  5х²+2х=0           В)  2-х-х²=0         Г)  4х²+5х-3=0

9. Розв`яжіть рівняння    5х²=0 А)  -15                       Б)  0                      В)  немає коренів      Г) 

10. Розв`яжіть рівняння:    9х-х²=0

А)  немає коренів        Б)  0; -9                   В)  0; 9        Г)  3; -3

Таблиця правильних відповідей

№ задания	1	2	3	4	5	6	7	8	9	10
1 вариант	Б	Г	Г	Б	А	Б	Г	А	А	А
2 вариант	Г	Б	В	В	В	Г	Б	А	Б	В

VІ. Рефлексія. Підведення підсумків уроку. Підсумок уроку

• Сформулюйте означення повного квадратного рівняння

• У рівнянні 3х²-7х+2=0 назвіть коефіцієнти а, в, с.

• Запишіть рівняння, якщо в=0, а=-1, с=2.

• Як називається таке рівняння?

• Наведіть приклади інших неповних квадратних рівнянь.

• Скільки коренів мають рівняння ах²=0, ах²+вх=0, ах²+с=0?

На сьогоднішньому уроці я дізнався …

На сьогоднішньому уроці найцікавішим для мене було …

Як я оцінюю свою роботу за 100 бальною шкалою;

Які риси характеру допомагали навчатися, а які заважали?                                            

Активність, апатія, ввічливість, упертість, дисциплінованість, допитливість, ініціативність, наполегливість, неуважність,незібраність, недбалість, організованість

VІІ. Домашнє завдання

§19,  №869(а,б), №873(а,в), №876(А), №886(Б)