ЗМІСТ

ВСТУП ------------------------------------------------------------------------------------------------------3      

РОЗДІЛ 1 

ЗВИЧАЙНІ ОЗНАКИ ПОДІЛЬНОСТІ

1.1. Загальні зауваження -------------------------------------------------------------------------------7      

1.2. Ознаки подільності на 2, 5, 4, 8 ------------------------------------------------------------------8 

1.3. Ознаки подільності на 3, 9 і 11 ------------------------------------------------------------------9      

1.4. Ознака подільності на 7 -------------------------------------------------------------------------11      

1.5. Загальна ознака Паскаля -----------------------------------------------------------------------12      

1.6. Ознака подільності на 13 ------------------------------------------------------------------------12     

1.7. Ознаки подільності на 7, 11, 13 ----------------------------------------------------------------13      

1.8. Ознака подільності на 19 ------------------------------------------------------------------------14     

РОЗДІЛ---------------------------------------------------------------------------------------------------------------------- 2 

СПЕЦІАЛЬНІ ОЗНАКИ ПОДІЛЬНОСТІ -----------------------------------------------------------------------

2.1. Теорема Ферма---------------------------------------------------------------------------------------------------- 16  

2.2. Функція і теорема Ейлера------------------------------------------------------------------------------------- 17  

2.3. Теорема Вільсона------------------------------------------------------------------------------------------------- 18 

РОЗДІЛ 3   ЗАДАЧІ НА ЗАСТОСУВАННЯ ОЗНАК ПОДІЛЬНОСТІ------------------------------ 19  

ВИСНОВКИ-------------------------------------------------------------------------------------------------------------- 22 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ----------------------------------------------------------------------- 24  

 

ДОДАТКИ ------------------------------------------------------------------------------------------------25      

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

Подільність — фундаментальна властивість натуральних та цілих чисел. Число a ділиться на b, відповідно, число b є дільником a, якщо частка  — ціле число. Будь-яке натуральне число ділиться на одиницю і на себе. Якщо дане число не має інших дільників, то таке число називається простим, в іншому разі — складеним. Властивості простих чисел і питання подільності

Піфагор  

займали думки науковців і філософів протягом двох з половиною тисячолітть, принаймні з часів Піфагора, і ще досі не вичерпали себе. Завдяки розвитку криптографії і розповсюдженню заснованних на теорії чисел алгоритмів, пов'язані з перевіркою на простоту і факторизацією дослідження знаходяться на передовому краю 

                                                                   Питання         подільності         натуральних         чисел

розглядалися уже в античні часи. Евкліду належить один з найвідоміших результатів математики, твердження, що не існує найбільшого простого числа, тобто множина простих чисел — нескінченна. Він також навів найперший в історії алгоритм, а саме алгоритм Евкліда знаходження найбільшого спільного дільника двох натуральних чисел.          

Цікаво відзначити, що це — не тільки найдавніший,

Евклід а й один з найефективніших алгоритмів в математиці, який

майже не був вдосконалений за більш ніж дві тисячі років, що минули по тому. Але набагато раніше за Евкліда, Піфагор і піфагорейці розробили теорію досконалих і дружніх чисел, які відігравали важливу роль у їх філософській системі.

Подільність чисел, більш загальних ніж цілі, було ретельно досліджено у 19 ст., починаючи з роботи Гауса про властивості гаусових цілих чисел, комплексних чисел вигляду a + bi, де — це звичайні цілі числа, а

— це уявна одиниця. Гаус відкрив аналог алгоритма Евкліда і в

такий спосіб довів однозначність факторизації гаусових цілих чисел. Чимало із спроб доведення великої теореми Ферма спиралося на однозначність факторизації алгебраїчних цілих чисел вигляду

 

де ζ—це примітивний корінь з одиниці степені n,ζⁿ = 1, a — цілі числа. Однак виявилося, що у випадку загального

n такі числа поводяться набагато складніше, ніж звичайні цілі, зокрема, для них не виконується однозначність факторизації на прості множники. У роботах Куммера, Кронекера і Дедекінда з теорії подільності алгебраїчних цілих чисел з'явились фундаментальні для сучасної математики поняття теорії кілець, на яких, разом з введеним Галуа поняттям групи, ґрунтується сучасна абстрактна алгебра.

Арифметика і геометрія — давні супутники людини. Ці науки з'явилися тоді, коли виникла необхідність рахувати предмети, вимірювати земельні ділянки та час. Арифметика виникла в країнах стародавнього

Сходу: Вавілоні, Китаї, Індії, Єгипті. Наприклад, єгипетський папірус Рінда (названий на ім'я його власника Г. Рінда) належить до ХХ ст. до н. е. Серед інших відомостей він містить розклад дробів на суму дробів з чисельником — одиницею, наприклад:

 

Математичні знання накопичені в країнах стародавнього Сходу розвивалися далі вченими давньої Греції. Історія зберегла імена багатьох вчених, які займалися арифметикою в античному світі: Анаксагор, Зенон, Евклід, Архімед, Ератосфен, Діофант. Особливо варто виділити ім'я Піфагора, Піфагорійці (учні й послідовники Піфагора) обожнювали числа, вважаючи, що в них міститься вся гармонія світу. Окремим числам і парам чисел приписувалися особливі властивості. У великій пошані були числа 7 і 36, тоді ж було звернуто увагу на так звані ідеальні числа, дружні числа, тощо.

У середні віки розвиток арифметики також пов'язано зі Сходом: Індією, країнами арабського світу та Середньої Азії. Від індійців прийшли до нас цифри, якими ми користуємося, нуль і позиційна система числення; від альКаши (XV ст.), що працював в Самаркандскій обсерваторії Улугбека, — десяткові дроби. Завдяки розвитку торгівлі і впливу східної культури починаючи з XIII ст. підвищується інтерес до арифметики і в Європі. Так твір італійського вченого Леонардо Пізанського (Фібоначчі) «Книга абака» знайомив європейців з основними досягненнями математики Сходу і став початком багатьох досліджень в арифметиці і алгебрі.

  Водночас з винаходом книгодрукування (середина XV ст.) з'явилися перші друковані книги з математики. Перша друкована книга з арифметики була видана в Італії в 1478 р. В «Повній арифметиці» німецького математика М. Штифеля (початок XVI ст.) вже є від'ємні числа навіть ідея логарифмування. Приблизно з XVI ст. розвиток арифметики зливається з алгеброю. Значними подіями були праці Франсуа Вієта, у яких числа позначені літерами. Починаючи з

Підручник з арифметики цього часу основні арифметичні правила Леонтія Магницького усвідомлюються вже остаточно з позицій алгебри.

Основний об'єкт арифметики — число. Натуральні числа виникли з рахунку конкретних предметів. Минуло багато тисячоліть, перш ніж люди засвоїли, що два птахи, дві руки, двоє людей можна назвати одним і тим же

словом     —     «два».     Важливе     завдання     арифметики     —     навчитися

абстрагуватися від форми предметів, їх розміру, кольору. Вже у Фібоначчі є задача: «Сім жінок йдуть у Рим. У кожної по 7 мулів, кожен мул несе по 7 мішків, в кожному мішку по 7 хлібів, в кожному хлібі 7 ножів, кожен ніж в 7 ножнах. Скільки всіх?» Для розв'язку цієї задачі додати жінок мулів, мішки і хліби. Розвиток поняття числа — поява нуля і від'ємних чисел, звичайних і десяткових дробів, способи запису чисел (цифри, позначення, системи числення) — все це має багату і цікаву історію.

У арифметиці числа додають, віднімають, множать і ділять. Мистецтво швидко і безпомилково виконувати ці дії над будь-якими числами довго вважалося найважливішим завданням арифметики. В наш час усно чи на папері ми робимо лише найпростіші обчислення, а складніші — за допомогою обчислювальної техніки.

Серед важливих понятть, які запровадила арифметика, були пропорції та відсотки. Більшість понять і методів арифметики ґрунтується на залежностях між числами. У історії математики процес злиття арифметики і геометрії відбувався протягом багатьох століть. Можна чіткопростежити «геометризацію» арифметики: складні правила і закономірності, виражені формулами, стають зрозумілішими, якщо вдається зобразити їх геометрично. Велику роль у самій математиці і її додатках відіграє зворотний процесс — переклад геометричної інформації на мову чисел (див. Графічні обчислення). В основі цього перекладу лежить ідея французького філософа і математика Рене Декарта визначення точок на площині координатами. Зрозуміло, до нього ця ідея вже використовувалася, приміром в морській справі, коли треба було визначити місцезнаходження корабля, а також астрономії, геодезії. Але саме від Декарта і його учнів йде послідовне застосування мови координат. І в наш час при управлінні складними процесами (наприклад, польотом космічного апарату) воліють мати всю інформацію в вигляді чисел, які й обробляє обчислювальна машина.

 

 

 

 

 

РОЗДІЛ 1 

ЗВИЧАЙНІ ОЗНАКИ ПОДІЛЬНОСТІ

 

1.1. Загальні зауваження 

Як відомо, сума, різниця і добуток цілих чисел завжди є число ціле, тоді як їх частка може бути як цілим, так і дробовим числом. У зв'язку з цим часто виникає потреба з'ясувати, при якій умові частка цілих чисел а і b є число ціле.

Ціле число а ділиться на ціле число b, якщо існyє таке ціле число с, що

 . Якщо а ділиться на b, то записують це так:  (або b  —

читається: b ділить а). При цьому а називають діленим, a b — дільником числа а.

                 Наприклад, 75 15 (тому що 75 = 15 5);                  

(оскільки   ; 0 0 (тому що       де k — довільне ціле число).

Запис а b означає, що а не ділиться на b. Так, 75 10, 2 0,            і т. д.

З означення подільності чисел випливають такі властивості:

а) якщо а b, a b с, то а с;

б) якщо а с і b с, то (а + b с і (а — b)с;

в) якщо а с або b с, то ab с.

Ці властивості треба обґрунтовувати, виходячи з означення подільності чисел. Обгрунтуємо, наприклад, першу властивість. За умовою а b, b с. Це означає, що а =bk, b = cm, де k, m — цілі числа. Тоді а =(cm) k = с n, де n = km

— ціле число. Тому, за означенням ас.

При встановленні ознак подільності використовуватимемо твердження:  якщо ціле число N подано у вигляді

N = mq + aN₁, де а і т — взаємно прості числа (зокрема, а може дорівнювати 1 або    , то Nт тоді і тільки тоді, коли N₁т.

Справді, якщо N т, то mq + aN₁ ділиться на т і, отже, aN₁т. Але а, т — взаємно прості числа, тому N₁т.

Навпаки, якщо N₁т, то з N = mq + aN₁ випливає, що Nт.

Отже, на основі попереднього твердження, питання про подільність числа N на т зводиться до питання про подільність N₁ на т. Якщо при цьому N₁ має менш складну будову, ніж число N, то досліджуючи число N₁ роблять певні висновки про подільність N на т, або, інакше кажучи, формулюють певну ознаку подільності числа N на т.

Зауважимо, що ознаку подільності на число т досить формулювати, якщо т є просте число (в окремих випадках формулюють ознаку подільності при умові, що т є степінь простого числа, наприклад: 4, 8, 9, 25, ...). Справді, якщо m = ab, де a, b — взаємно прості числа, і N ділиться на а і на а, то N ділиться на добуток чисел а, b, тобто на т. Отже, досить з'ясувати подільність числа N окремо на а і на b.

 

1.2. Ознаки подільності на 2, 5, 4, 8 

Нехай  — запис числа N у десятковій системі

числення, тобто

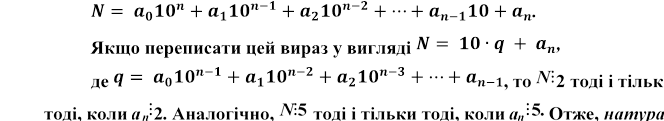
число N (записане в десятковій системі числення) ділиться на 2 (на 5) тоді і тільки тоді, коли остання цифра цього числа ділиться на 2 (на 5). Запишемо тепер число N у вигляді

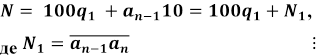. Враховуючи, що 100 4, робимо висновок: число N

ділиться на 4 тоді і тільки тоді, коли дві його останні цифри утворюють число, яке ділиться на 4. Враховуючи, що

              = ,

ознаку подільності на 4 формулюють іноді ще так: число N ділиться на 4 тоді і тільки тоді, коли сума цифри одиниць та подвоєної цифри десятків цього числа ділиться на 4.

Так, 19724, тому що 2 + 27 = 16 4; 197474, оскільки 27 + 4 = 184.

Тепер число N запишемо так:

 .

Отже, число N ділиться на 8 тоді і тільки тоді, коли три його останні

цифри утворюють число, яке ділиться на 8. Або, враховуючи рівність

,

ознаку подільності на 8 формулюють ще так:  число ділиться на 8 тоді і тільки тоді, коли сума цифри одиниць, подвоєної цифри десятків та почетвереної цифри сотень ділиться на 8.

Наприклад,   15 736 8 тому,   що 6+23 + 47=40 8; 19728, оскільки  2 + 27 + 49 = 52 8. 

 

1.3. Ознаки подільності на 3, 9 і 11  

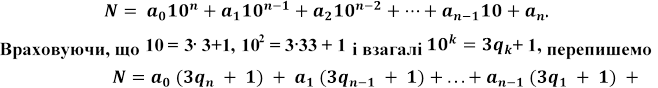Нехай

число N так:

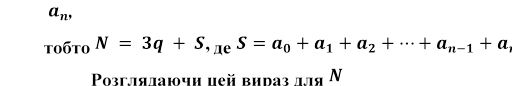, робимо висновок, що N 3 тоді і тільки

тоді, коли S3. Але S — сума цифр числа N. Отже, число N ділиться на 3 тоді і тільки тоді, коли сума цифр цього числа ділиться на 3.

Аналогічно, якщо т = 9, то при довільному натуральному k  +1.

Міркуючи аналогічно, матимемо:

 . Як бачимо, ознака

подільності числа N на 9 така сама, як і ознака подільності на 3: число N ділиться на 9 тоді і тільки тоді, коли сума цифр цього числа ділиться на 9. Нехай тепер т=11. Покажемо, що при довільному натуральному s

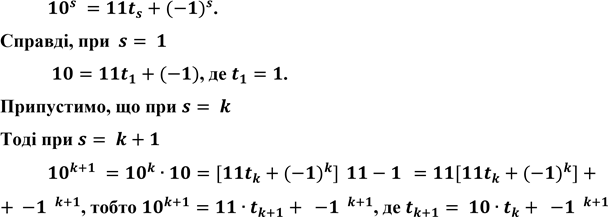
Отже, на основі принципу математичної індукції, рівність

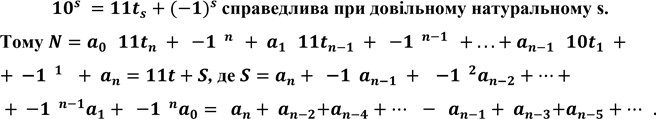
Отже, S дорівнює різниці між сумою цифр числа N, які стоять на непарних місцях і сумою цифр цього самого числа, що стоять на парних місцях (якщо починати рахунок з цифри одиниць, aле це не обов'язково — можна починати рахунок з цифри одиниць найвищого розряду, в результаті чого може змінитися тільки знак числа S).

З попереднього робимо висновок: число N ділиться на 11 тоді і тільки тоді, коли різниця між сумою цифр цього числа, які розміщені на парних місцях і сумою цифр, що розміщені на непарних місцях, ділиться на 11.

Приклад. Нехай = 1 234 567 890. Тут S = (0+8+6+4+2)(9+7+5+3+1) =

=2025 = 5 11. Отже, N

Зауважимо, що виписувати цифри «з кінця» не завжди зручно.

Врахуємо попередні пояснення. Тоді для того самого числа N маємо: 

S' = (1 +3 + 5 + 7 + 9)  (2 + 4 + 6 + 8 + 0) = 25  20 = 511. Висновок той

самий.   1.4. Ознака подільності на 7  Міркуючи як і раніше, встановлюємо:
10 = 7q1 + 3,   102 =7q2 + 2,   103 =7q3 – 1, 104 =7q4 – , 105 =7q – 2,	106 =7q6 + 1, 107 =7q7 + 3, 108 =7q8 + 2, 109 =7q9 – 1, ……………

₅

Ці рівності можна дістати в результаті безпосередніх обчислень або комбінуючи вже відомі результати. Наприклад,

 

.

 

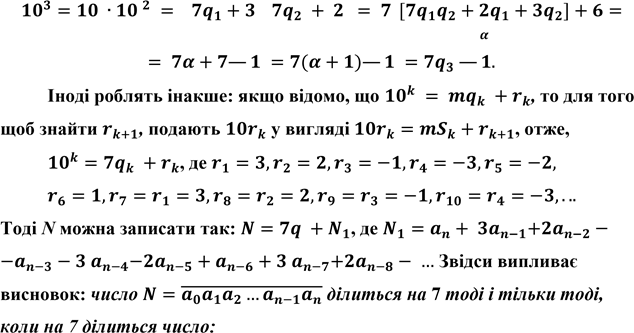
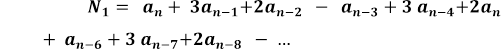
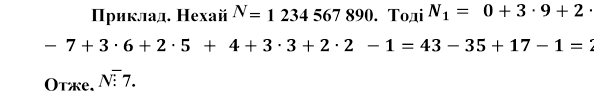1.5. Загальна ознака Паскаля 

Раніше, встановлюючи ознаку подільності N на т, ми подавали  у

записували так: , де

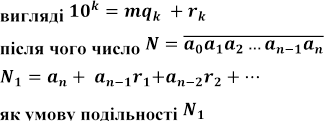, і формулювали ознаку подільності N на т

 на т: число Nт тоді і тільки тоді, коли т. Сформульовану таким чином ознаку подільності називають загальною ознакою Паскаля. Якщо т якесь конкретне число, то і числа   

відповідно набувають певних конкретних значень. В результаті маємо ту або іншу конкретну ознаку подільності (на 2, 3, 5, 7, 9, 11 і т. д.).

      Наприклад, якщо             або           , то      = 1(k = 1, 2, 3, ...); при  

(k= 1, 2, З, ...) і т. д.

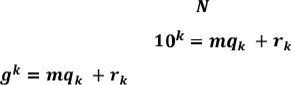Цю ознаку подільності неважко сформулювати у довільній системі числення: якщо число       записано у системі числення з основою , то замість рівностей          треба користуватися рівностями

 (k = 1, 2, З, ...).

 

1.6. Ознака подільності на 13 

Міркуючи так само, як і при встановленні ознаки подільності на 7, маємо:

                      10 = 13q₁ –3,                                                 10⁶ =13q₆ + 1,

 

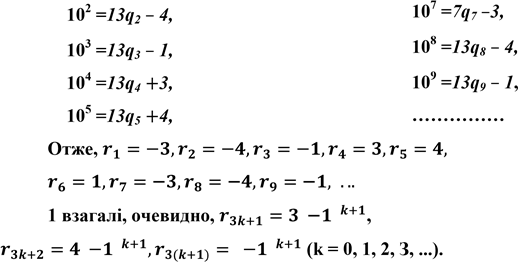
Тоді (див. загальну ознаку Паскаля)  

   (*)

Таким чином, число N 13 тоді і тільки тоді, коли число , яке

визначається рівністю (*), ділиться на 13.

Наприклад, якщо N = 123 456 789, то

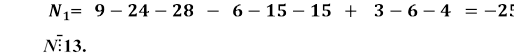 , а отже, число

Зауважимо, що . Це означає, що при діленні N на 13 ми дістанемо остачу, яка дорівнює 1.

 

1.7. Ознаки подільності на 7, 11, 13 

Розглянуті раніше ознаки подільності на 7 і 13 не зовсім зручні для запам'ятовування і для користування. Далі виведемо більш зручну для запам'ятовування спільну ознаку подільності на 7, 11, 13. 

             д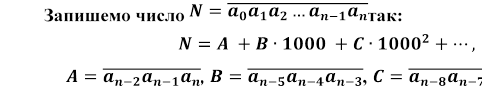е        .

Використовуючи рівності:

1000 = 1001q₁ –1,  

10002 =1001q₂  1, 

...............................

10003 =1001q_k +    , перепишемо число      у вигляді

                                                                        , де                                     

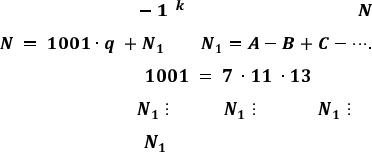Враховуючи, що , робимо висновок, що N7 (або N11, або N13), якщо 7 (або 11, або 13.

Щоб мати число  треба задане число N розбити на числа по 3 цифри в кожному (починаючи з кінця) і утворити алгебраїчну суму, беручи сусідні числа з протилежними знаками.

Наприклад, якщо N = 9 876 543 210, то А = 210, В = 543, С = 876, D = 9.

Тоді .

Число 1200 не ділиться на жодне з чисел 7, 11, 13. Отже, N також не ділиться на ці числа.

 

1.8. Ознака подільності на 19 

Розглянемо ознаку подільності на 19, запропоновану студентом коледжу із Східної Африки Казангакі. Цей метод полягає у тому, що для з'ясування подільності числа  на 19 треба закреслити останню

цифру цього числа і до числа, що залишилось, додати подвоєну викреслену цифру. Якщо здобуте таким чином число ділиться на 19, то задане число N теж ділиться на 19. Отже,   питання  про подільність   числа 

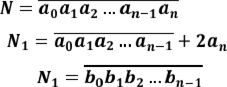на 19 зводиться до питання про подільність на 19

числа . Якщо при цьому в десятковій системі числення   , то питання про подільність на 19 числа  

можна звести до питання про подільність на 19 числа 

. Продовжуючи цей процес, дістанемо

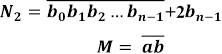двозначне число               . З'ясовуємо, чи ділиться воно на 19, чи ні.

Приклад 1. З'ясувати, ділиться на 19 число N = 123 456 789.

 = 12 345 678 + 29 = 12 345 696; 

 = 1 234 569 + 12 = 1 234 581; 

 = 123 458 + 2 = 123 460;

= 12346 + 0 = 12 346;

 = 1234 + 12 = 1246; 

= 124 + 12 = 136; 

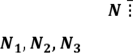                       = 13+ 12 = 2519. Отже, і задане число      19.

Процес знаходження чисел    … можна проводити у більш зручній формі: 

Приклад 1. З'ясувати, ділиться на 19 число  M= 3 086 379.

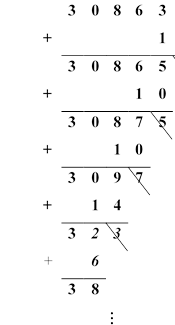38 19. Отже, 3 086 37919.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2 

СПЕЦІАЛЬНІ ОЗНАКИ ПОДІЛЬНОСТІ

 

 Вище розглядались ознаки подільності, що грунтуються на знаннях запису досліджуваного числа N у тій або іншій системі числення. Разом з тим часто доводиться мати справу з числами, запис яких у відповідній системі числення не завжди зручний або й неможливий. Наприклад, запис числа

           >        у десятковій системі числення міститиме більше, ніж 10⁸ цифр. Для запису цього числа треба було б більш ніж 50 000 сторінок по 40 рядків, у кожному з яких записано по 50 цифр. Отже, потрібно було б не менш 50 томів по 1000 сторінок у кожному, щоб записати це число. Тому дослідження таких чисел, записаних у десятковій системі числення, просто неможливе. Нижче ми розглянемо умови подільності, не пов'язані із записом чисел у певній системі числення.

 

2.1. Теорема Ферма 

Якщо р — просте число і ар, то

р.

Наприклад, якщо а = 2, р = 7, то   7. Справді, 7.

Теорема Ферма використовується тоді, коли треба знайти остачу від ділення одного числа на інше. Покажемо це на прикладі.

Отже, остача від ділення 3¹⁹⁷⁴ на 19 дорівнює 11.

 

2.2. Функція і теорема Ейлера 

Позначимо через  кількість натуральних чисел, що не перевищують т і взаємно прості з т. Наприклад, , тому що є тільки 4 натуральних числа, що не перевищують 10 і взаємно прості з 10: 1, 3, 7, 9. Аналогічно:

                                                                                    ,

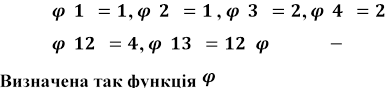                                                           ,  (р) = р  1 (р — просте число) і т. д.

(т) називається функцією Ейлера. Вона відіграє

надзвичайно важливу роль у дослідженні питань подільності чисел. Якщо відомий канонічний розклад числа т на прості множники:

 , то значення функції Ейлера від т можна

знайти за формулою

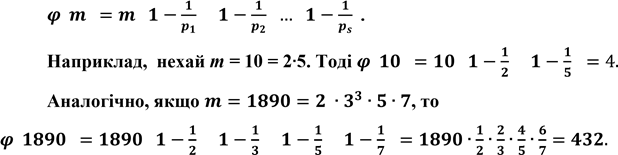
Теорема Ейлера. Якщо ціле число а і натуральне число т взаємно

прості, то  

Наприклад, якщо а = 5, т = 12, то 

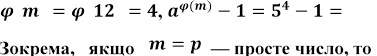
 624 12.    

. Отже,

теорема Ферма є окремим випадком теореми Ейлера.

Сформульована теорема застосовується під час досліджень багатьох питань арифметики і, зокрема, при знаходженні остачі від ділення одного числа на інше.

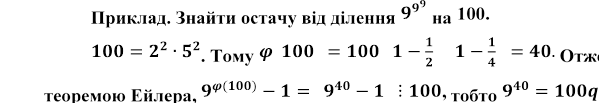
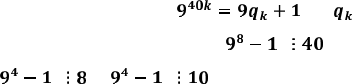Підносячи обидві частини останньої рівності до довільного натурального степеня k, матимемо:       , де     залежить від вибору числа k.

                Покажемо тепер, що                       . Справді, . Тому

 і         і, отже, 9⁴— 1 ділиться на найменше спільне кратне чисел 8 і 10, тобто на 40. Тоді

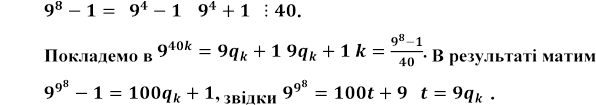
. Тому

в свою чергу, означає, що дві останні цифри числа  записаного в

десятковій системі числення, дорівнюють 8 і 9, тобто 

.

 

2.3. Теорема Вільсона 

Позначимо через п! добуток усіх натуральних чисел від 1 до п:

п! = 1 2 3 ... п (0! = 1).

Тоді справджується така теорема.

Теорема Вільсона. Число (р — 1)! + 1 ділиться на р тоді і тільки тоді,

коли р — просте число.

Наприклад, якщо р = 5, то (5— 1)! + 1 =4!+1= 24+1=25 5; якщо р = 7, то (7— 1)! + 1=6!+1 = 720+1=7217 і т. д.

 

 

 

РОЗДІЛ 3 ЗАДАЧІ НА ЗАСТОСУВАННЯ ОЗНАК ПОДІЛЬНОСТІ

 

1.   Стійка подільність

Яке найменше число треба задумати, щоб після збільшення його на 7 або на 19 результат ділився відповідно на 7 або на 19, після зменшення на 17 результат розділився б на 17, а після ділення його на 11 і результат розділився б на 11?

Розв’язання:

Очевидно, що задумане число повинне ділитися на 7, 19, 17 і двічі на 11.

Найменшим таким числом є . Легко

перевірити, що його подільність на свої множники зберігається як при збільшенні на 7 або 19, так і при зменшенні на 17.

 

2.  

На одне ділиться, на інше ні

Знайдіть найменше число, яке ділиться на 77, а при діленні на 74 дає в залишку 48.

Розв’язання:

Запишемо шукане число у вигляді , і розчленуємо його на два доданки: . Найменше відповідне значення  = 16, тоді 

3 = 48.

Значить, шукане число .

 

3.   Ділення на шість

Доведіть, що число  ділиться на 6.

Розв’язання:

Маємо . Це є добуток трьох

послідовних натуральних чисел, з яких одне обов'язково кратне 3 і хоча б одне парне. Добуток ділиться на 3 і на 2, отже, і на 6.

 

4.   Ділення на сім

Діляться на 7 числа вигляду:

1)                        , якщо  ділиться на 7;

2)                        якщо сума цифр ділиться на 7;

3) 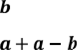                       , якщо  — двозначне число і  ділиться на 7;

4)                        , якщо  ділиться на 7. 

Доведіть істинність цих тверджень.

Розв’язання: 

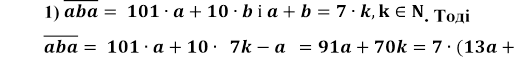 ділиться на 7.

2), 3), 4) Доведення аналогічне.

 

5. Доведіть!

Доведіть, що число , ділиться на 6, а число , ділиться на 30.

Розв’язання:

Представимо . Оскільки в правій частині

рівності перший доданок є добуток трьох послідовних натуральних чисел, то обов'язково одне з них ділиться на 2, а інше — на 3. Другий доданок ділиться на 6.

Значить,                 ділиться на 6. 

Представимо                                                           .

Будь-яке натуральне  > 1 можна представити як               , або , або

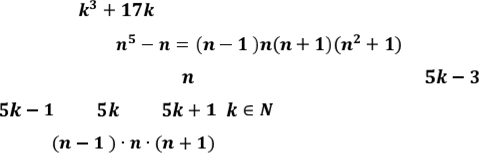, або          , або ,         . Добуток трьох послідовних натуральних чисел      завжди кратний 6, а при  

він, окрім того, кратний 5, отже, він кратний 30. При решті значень

 2 добуток, залишаючись кратним 6, не буде кратним 5,

та зате стає кратним 5 останній множник заданого числа, а саме 

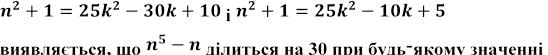. Таким чином,

.

6. Зніміть маску з однієї цифри

У записі знаменитого «шахового» числа  

на його другу цифру накинута маска у. Знявши маску, розшифруйте значення у, знаючи, що достатньо збільшити задане число на 3 одиниці, як воно стає кратним числу 19. 

Примітка. По легенді саме таке число пшеничних зерен слідувало видати в нагороду винахіднику шахів, що попросив покласти всього одне зерно на першу клітку шахівниці, а на кожну наступну клітку удвічі більше число зерен, ніж на попередню.

Розв’язання:

Застосовуємо послідовно ознаку подільності на 19.

Одержали трьохцифрове число, у якого 0 одиниць,  десятків і

одна сотня. Таке число ділиться на 19 тільки тоді, коли  (190 ділиться на 19). Інший вираз

«шахового» числа: .

 

   

 

 

ВИСНОВКИ

 

Подільність — фундаментальна властивість натуральних та цілих чисел. Властивості простих чисел і питання подільності займали думки науковців і філософів протягом двох з половиною тисячолітть, принаймні з часів Піфагора, і ще досі не вичерпали себе. Завдяки розвитку криптографії і

розповсюдженню заснованних на теорії чисел алгоритмів, пов'язані з перевіркою на простоту і факторизацією дослідження знаходяться на передовому краю. В своїй роботі я розлянула ознаки подільності натуральних чисел. Ознакою подільності називається правило, за допомогою якого можна встановити подільність одного числа на друге, не виконуючи ділення.

Суть всякої ознаки подільності на дане число b полягає у тому, що при ‘його допомозі питання про подільність будь-якого числа а на b зводиться до питання про подільність на b деякого числа, меншого ніж а. (Неважко бачити, що перевірка подільності звичним діленням також заснована на цій ідеї.)

Таким чином, ознака подільності є математичним об'єктом вельми поширеної, хоча і не впадаючої в очі природи. Це не формула, не теорема, не означення, а деякий процес. Деякі ознаки подільності, поза сумнівом, відомі. Метою цієї роботи є розгляд різних ознак подільності, головним чином з принципової сторони.

В своїй роботі я навів доведення основних ознак подільності натуральних чисел, приклади їх застосування для встановлення подільності одного числа на інше, а також при розв’язуванні задач підвищеної складності на доведення подільності чисел, або ж на знаходження остачі від ділення чисел, яку звичним способом знайти практично неможливо. 

А також зробив систематизацію ознак подільності натуральних чисел у вигляді таблиці подільності (Додаток 1), побудувала алгоритм застосування деяких ознак подільності (Додатки 2, 3), а також класифікувала ознаки за спільним принципом (Додаток 4). 

Матеріали моєї роботи можна використати на уроках математики при вивченні теми «Подільність натуральних чисел», а також для проведення фркультативних та гурткових занять з математики та при підготовці до математичних олімпіад.  

 

          

 

 

 

  

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1.                   Б.А. Кордемський, А.А. Ахадов Удивительный мир чисел ― Москва «Просвещение», 1986. С.84.

2.                   О.В. Кужель Розвиток поняття про число Ознаки подільності Досконалі числа ― Видавниче об’єднання «Вища школа»  Київ ― 1974. С.46-63.

3.                   В.В. Воробьев Признаки делимости ― Москва «Наука», 1988. С.52-58.

4.                   В.А. Вишенський, М.О. Перестюк, А.М. Самойленко Збірник задач з математики ― Київ «Либідь», 1993. С.4-20.

5.                   А.Г. Мерзляк, В.Б. Полонський, М.С. Якір Математика          6 клас ― Харків «Гімназія», 2006. С.9-20.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК 1 

ТАБЛИЦЯ ПОДІЛЬНОСТІ

 

Дільник                     Умова подільності

2                         Остання цифра є парною (0, 2, 4, 6, або

8).

3                         Сума цифр повинна ділитися на 3.

4                         Якщо число, утворене двома останніми цифрами ділиться на 4.

5                         Остання цифра або 5 або 0.

6                         Якщо число ділиться і на 2, і на 3.

7                         Число розбивається на блоки по три цифри, починаючи з кінця. Число ділиться на 7, якщо різниця суми блоків, що стоять на парних місцях, і суми блоків, що стоять на непарних місцях, ділиться на 7. Якщо сума подвоєного числа без останніх двох цифр і останніх двох цифр ділиться на 7.

Якщо сума числа без останньої цифри і останньої цифри, помноженої на 5, ділиться на 7.

Різниця між числом без останньої цифри і подвоєної останньої цифри повинна ділитись на 7.

8                         Якщо число, утворене останніми трьома цифрами, ділиться на 8. Якщо число сотень є парне, то число, утворене двома останніми цифрами повинне ділитись на 8.

Якщо число сотень є непарним, то до числа, утворенного двома останніми цифрами, потрібно додати 4. Таке число повинне ділитись на 8.

 

9                         Сума всіх цифр повинна ділитись на 9.

10                    Остання цифра 0.

 

Приклади

1   294: 4 є парне.

405: 4 + 0 + 5 = 9. 9 ділиться на 3.

2   092: 92 ділиться на 4.

490: остання цифра 0. 24: число ділиться на 2 і на

3.

2 911 272: 911 - (2 + +272) = =637. 637 ділиться на 7.

364: (3x2) + 64 = 70. 70 ділиться на 7.

364: 36 + (5×4) = 56. 56 ділиться на 7.

364: 36 − (2×4) = 28. 28 ділиться на 7.

5 128: 128 ділиться на 8.

624: 6 - парне, 24 ділиться на 8.

352: 52+4 = 56. 56 ділиться на 8.

2 880: 2 + 8 + 8 + 0 = =18. 18 ділиться на 9.

130: остання цифра 0.

11                    Число розбивається на блоки по дві    627: 6 + 27 = 33. 33 ділиться цифри, починаючи з кінця. Сума блоків на 11. повинна ділитись на 11.

 

Якщо різниця між числом без останньої 627: 62 - 7 = 55. 55 ділиться цифри і останньою цифрою ділиться на на 11.

11.

 

Якщо сума цифр, що стоять на парних         182 919: (9 + 9 + 8) –  місцях відрізняється від суми цифр, що        -(1 + 2 + 1) = 22. стоять на непарних місцях, починаючи з кінця, на число, що кратне 11.

 

12                    Якщо число ділиться на 3 і на 4.          324: воно ділиться і на 3, і

на 4.

Число без останньої цифри множать на        324: (32x2) − 4 = 60. 60 два і віднімають останню цифру. Таке        ділиться на 12.

число повинне ділитись на 12.

 

13                    Число ділиться на блоки по три цифри,        2 911 272: 911-(2+272) = 637.

починаючи з кінця. Сумуються блоки,         637 ділиться на 13. що стоять на парних і непарних місцях. Різниця цих сум повинна ділитись на

13.

 

До числа без останньої цифри додають         338: 33 + (8×4) = 65. 65 останню цифру, помножену на 4.         ділиться на 13. Утворене число повинне ділитись на 13.

 

Від числа без останньої цифри    637: 63 − (7×9) = 0. 0 віднімають останню цифру, помножену    ділиться на 13.

на 9. Утворене число повинне ділитись на 13.

 

14                                          Якщо число ділиться на 2 і на 7.                  224: воно ділиться на і на 2,

і на 7.

Число без останніх двох цифр множать         364: (3x2) + 64 = 70. на 2. До результату додають число, утворене двома останніми двома цифрами. Сума повинна ділитись на 14. 15              Якщо число ділиться на 3 і на 5.   390: число ділиться на 3 і на

5.

 

16                    Якщо число тисяч є парним, то 254 176: 176 ділиться на 16.

перевіряють число, складене з останніх трьох цифр.

Якщо число тисяч є непарним, то до   3 408: 408+8 = 416. 416 числа, утвореного останніми трьома     ділиться на 16. цифрами, додають 8.

Число без останніх двох цифр множать        176: (1x4) + 76 = 80. 80 на 4 і додають число, утворене        ділиться на 16. останніми двома цифрами. Результат повинен ділитись на 16.

17                    Число без останніх двох цифр множать        187: − (1x2) + 87 = 85. 85        на 2 і додають число, утворене ділиться на 17.

     останніми двома цифрами. Результат повинен ділитись на 17.

 

                    Від числа без останньої цифри                    85: − 8 + (5×5) = 17.

віднімають останню цифру, помножену на 5. Результат повинен ділитись на 17.

 

Число ділиться на 17 тоді і тільки тоді,         29053: 2905+36=2941; коли число його десятків, складене із 294+12=306; 30+72=102; збільшеним в 12 разів числом одиниць,       10+24=34. Оскільки 34

                    кратне 17.                                                      ділиться на 17, то і 29053

ділиться на 17.

18                    Якщо число ділиться на 2 і на 9.          342: воно ділиться і на 2, і

на 9.

19                    До числа без останньої цифри додають         437: 43 + (72) = 57. 57 подвоєну останню цифру. Результат          ділиться на 19. повинен ділитись на 19.

20                    Якщо число ділиться на 10 і число      360: число ділиться на 10 і 6 десятків є парне.    є парним.

 

Якщо число, утворенне двома    480: 80 ділиться на 20. останніми цифрами ділиться на 20.

22                    Якщо число закінчується на парну      6886: ділиться на 11 і цифру й ділиться на 11. закінчується парною цифрою.

23                    Число ділиться на 23 тоді і тільки тоді,         28842 ділиться на 23,    коли число його сотень, складене з      оскільки 288 + (342) = 414 потрійним числом десятків, кратне 23.         продовжуємо

4 + (314) = 46 очевидно ділиться на 23.

25                    Якщо число, складене з двох останніх 134 250: 50 ділиться на 25. цифр, ділиться на 25.

26                    Якщо число ділиться на 13 і є парним.         2 911 272: число ділиться на 13 і є парним.

27                    Число ділять на блоки по три цифри, 2 644 272: 2+644+272 = 918.

починаючи з кінця. Сума утворених   918 ділиться на 27. блоків повинна ділитись на 27.

Від числа без останньої цифри    621: 62 − (1×8) = 54. 54 віднімають останню цифру, помножену        ділиться на 27. на 8.

 

32                    Якщо число десятків тисяч є парним, 41 312: 1312 ділиться на 32.

то перевіряють на подільність число, утворене останніми чотирма цифрами.

Якщо число десятків тисяч є непарним, 254 176: 4176+16 = 4192. то до числа, утвореного останніми      4192 ділиться на 32. чотирма цифрами, додають 16.

 

Число без останніх двох цифр множать        1 312: (13x4) + 12 = =64. 64 на 4 і до результату додають останні дві       ділиться на 32.

цифри. Суму перевір яють на подільність на 32.

33                    Якщо число ділиться на 11 і на 3.         1 003 002: число ділиться на

11 і на 3.

Число ділять на блоки по дві цифри,   627: 6 + 27 = 33. починаючи з кінця. Утворені блоками числа сумують. Результат повинен ділитись на 33.

 

37                                        Число ділять на блоки по три цифри, 2 651 272: 2 + 651 + 272 = починаючи з кінця. Число, утворені        925. 925 ділиться на 37.

блоками сумують. Сума повинна ділитись на 37.

 

                    Від числа без останньої цифри                    925: 92 − (511) = 37.

віднімають останню цифру, помножену на 11. Результат повинен ділитися на 37.

 

49                                        До числа без останньої цифри додають         1 127: 112 + (7×5) = 147. 147 останню цифру, помножену на 5. Таке          ділиться на 49. число повинне ділитись на 49.

Дільник	Умова подільності	Приклади
99	Розіб'ємо число на групи по 2 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп, вважаючи їх двозначними числами. Ця сума ділиться на 99 тоді і тільки тоді, коли саме число ділиться на 99.	53064 ділиться на 99, оскільки 5+30+64=99 ділиться на 99.
101	Розіб'ємо число на групи по 2 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп із змінними знаками, вважаючи їх двозначними числами. Ця сума ділиться на 101 тоді і тільки тоді, коли саме число ділиться на 101.	590547 ділиться на 101, оскільки 59-05+47=101 ділиться на 101.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                                                                                              

 

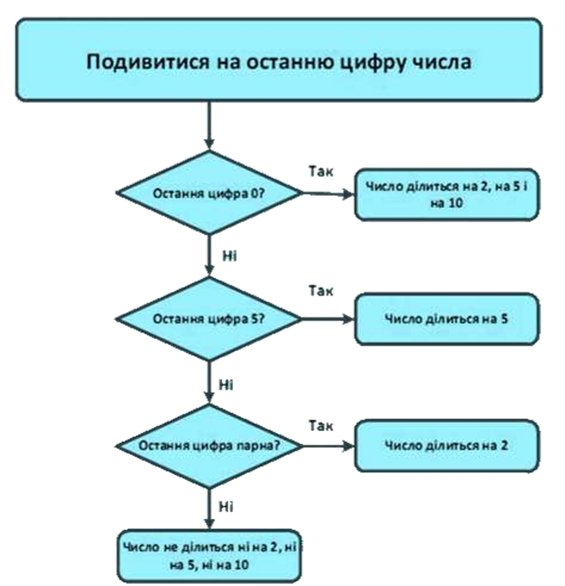
ДОДАТОК 2

Алгоритм визначення подільності на 10, на 2 і на 5

 

 

 

 

 

 

 

 

                                                                                                                                              

 

 

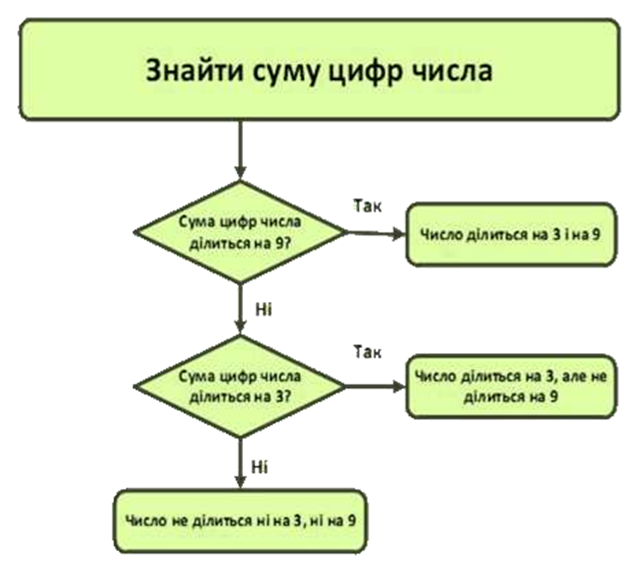
ДОДАТОК 3

Алгоритм визначення подільності на 3 і на 9

 

 

 

 

 

 

 

                                                                                                                                              

ДОДАТОК 4

КЛАСИФІКАЦІЯ ОЗНАК ПОДІЛЬНОСТІ

 

Визначення подільності по ОДНІЙ цифрі (на 10, на 2 і на 5)	Число а ділиться на 10  Остання цифра числа 0 Число а ділиться на 5  Остання цифра числа дорівнює 0 або 5 Число а ділиться на 2  Остання цифра числа – парна (парні цифри 0, 2, 4, 6, 8)
Визначення подільності по ДВОМ цифрам (на 4 і на 25)	Число а ділиться на 4         Дві останні цифри – нулі або утворюють число, кратне 4. Число а ділиться на 25       Дві останні цифри – нулі або утворюють число, кратне 25 (25, 50, 75).
Визначення подільності по ТРЬОМ цифрам (на 8 і на 125)	Число а ділиться на 8         Три останні цифри – нулі або утворюють число, кратне 8. Число а ділиться на 125     Три останні цифри – нулі або утворюють число, кратне 125 (125, 250, 375, 500, 625, 750, 875).
Визначення подільності за СУМОЮ цифр  (на 3 і на 9)	Число а ділиться на 3         Сума цифр числа а ділиться на 3 Число а ділиться на 9         Сума цифр числа а ділиться на 9

 

 

                                                                                                                                                                    

ДОДАТОК 5

ОЗНАКИ ПОДІЛЬНОСТІ НА n-у СТЕПІПЬ 2, 5 І 10

 

Ознака подільності на 10ⁿ-1

Розіб'ємо число на групи по n цифр справа наліво (у найлівішій групі може  бути від 1 до n цифр) і знайдемо суму цих груп, вважаючи їх n -значними числами. Ця сума ділиться на 10ⁿ - 1 тоді і тільки тоді, коли саме число ділиться на 10   ⁿ - 1.  

 

Наприклад:  

Оскільки           , то розіб'ємо число на групи по 2 цифри справа

наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп,  вважаючи їх двозначними числами. Ця сума ділиться на 99 тоді і тільки тоді,

 

коли саме число ділиться на 99.

 

53064 ділиться на 99, оскільки 5+30+64=99 ділиться на 99.

 

Ознака подільності на 10ⁿ+1

Розіб'ємо число на групи по n цифр справа наліво (у найлівішій групі може  бути від 1 до n цифр) і знайдемо суму цих груп із змінними знаками, вважаючи їх n -значними числами. Ця сума ділиться на 10_n   ⁿ + 1 тоді і тільки тоді, коли саме число ділиться на 10 + 1.   

Наприклад:  

Оскільки                  , то розіб'ємо число на групи по 2  

 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп із змінними знаками, вважаючи їх двозначними числами. Ця  сума ділиться на 101 тоді і тільки тоді, коли саме число ділиться на 101.

 

590547 ділиться на 101, оскільки  59-05+47=101 ділиться на 101.