Ознаки рівності трикутників
Розробка уроку з геометрії
Ознаки рівності трикутників
Вчитель математики –
Іванова Ірина Валеріївна
Ознаки рівності трикутників
Мета: повторити основні елементи трикутників та їх властивості, закріпити знання учнів теорем, що виражають ознаки рівності трикутників; виробити вміння аргументувати і доводити рівність трикутників із використанням ознак рівності трикутників; усвідомити практичність застосування ознак рівності трикутників; розвивати логічне мислення учнів; формувати навички чітко висловлювати думки.
Тип уроку: узагальнення та систематизація знань.
Хід уроку
Організаційний етап
Вітання, налаштування на роботу. Повідомлення мети, завдань уроку (в зошитах записують дату, тему уроку).
Мотивація навчальної діяльності
Один з найбільш визначних німецьких поетів та журналістів XIX століття Крістіан Йоганн Генріх Гейне говорив: «Недостатньо тільки отримувати знання, треба знати їх застосування. Недостатньо тільки бажати, треба діяти». Відповідно йому, відомий російський письменник Лев Миколайович Толстой писав: „Знання лише тоді знання, коли вони здобуті зусиллями своєї думки, а не тільки пам’яттю”.
Чи задумувались ви над тим, як знайти ширину озера, відстань між пунктами, яку не можна подолати прямолінійно? Тож, на сьогоднішньому уроці ми побачимо практичне застосування деяких правил, пов’язаних з трикутниками, розширимо свої знання, набудемо нових вмінь, тобто поринемо в історію знань про «Трикутник».
Актуалізація опорних знань
Перше завдання. Робота в группах. Кросворд. (кросворди намальовані на аркуші або на дошці, якщо достатньо місця)
Перед вами на дошці три аркуші з кросвордами. На кожну першу парту я кладу аркуш з запитаннями на які вам потрібно відповісти. По черзі один з учнів з кожної парти виходить до дошки та вписує ручкою відповідь, потім передає аркуш на наступну парту. Вам потрібно як швидше відгадати ключове слово у кросворді.
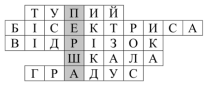
І група
|
1) Кут, що більше від прямого. |
2) Дуже швидко, дуже вміло кути навпіл поділила. |
3) Частину прямої візьмемо та фігурою назвемо. Не шматком – занадто різко, Тому назвемо її… |
|
|
|
4) Поділки з штрихами має, виміряти дозволяє. Масу, довжину і час – Все показує для нас. |
|
5) Температуру виміряй та виміряй кути. І на картах з географії зустрінеш його ти. |
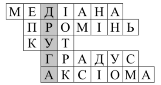
ІІ група
|
1) Відрізок починається З трикутника вершини. До точки йде на стороні, Точніше – до середини. |
2) Початок є, кінця немає. І сонечко його нам посилає. |
3) Куди дітей відправляють за порушення поведінки? |
|
|
|
4) Температуру виміряй та виміряй кути. І на картах з географії зустрінеш його ти. |
|
5) Їх ніколи не доводять, проте треба знати їх. В геометрії зустрінеш групу тверджень ти таких. |
ІІІ група
|
1) Як назвати кут такий, Що є меншим, ніж прямий? |
2) Довгоносий фігурист На аркуші ніби артист. Що танок – то кружок, Ти назви його, дружок. |
3) Їх у геометрії багато, І кожну треба добре знати. Які б ми не вивчали теми, Зустрінемо там… |
|
|
|
4) Відрізок швидко ти назви: З вершини йде до сторони. Прямий кут він шанує, зі стороною утворює. |
|
5) По ній довго можна йти, Кінця – краю не знайти. Початку теж нема, Бо це лінія - … |
Що об’єднує ці три слова? (Ознаки рівності трикутників). Вся геометрія з часів «Начал» Евкліда спирається на «трьох китах» - трьох ознаках рівності трикутників. Давайте їх пригадаємо. Кожна група сформулюйте свою ознаку (Один учень з групи формулює ознаку).
Друге завдання. Усно Вправа «Доведи рівність».
На дошці заздалегідь дані малюнки або прикріплені аркуші з малюнками.
|
|
|
|
|
|
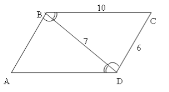
Доведіть рівність трикутників. Знайдіть периметр ∆ABD. |
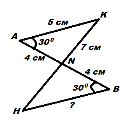
Доведіть рівність трикутників. Знайдіть BН. |
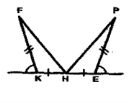
Доведіть рівність трикутників. |
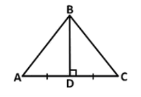
Доведіть, що АВС рівнобедрений |
Третє завдання. Усно Вправа «Знайди пару»
Утворить правильні твердження, об’єднавши їх початок (1—4) та кінець (А—Д).
|
1 |
Якщо у трикутника лише дві медіани рівні, то цей трикутник |
А |
тупокутний |
|
|
2 |
Якщо у трикутника одна медіана дорівнює половині сторони, до якої вона проведена, то цей трикутник |
Б |
рівнобедрений, відмінний від рівностороннього |
|
|
3 |
Якщо у трикутника три медіани рівні, то цей трикутник |
В |
прямокутний |
|
|
4 |
Якщо точка перетину висот трикутника лежить поза ним, то це трикутник |
Г |
рівносторонній |
|
|
|
|
Д |
гострокутний, відмінний від рівностороннього |
|
|
Відповідь |
1-Б; 2-В; 3-Г; 4-А |
|||
Удосконалення вмінь і навичок учнів. Розв'язування задач
Геометрія з давніх-давен є наукою піднесеною, таємничою та романтичною, а пошук способів розв'язання геометричних задач завжди був творчим, дослідницьким процесом. Бо для розуму немає нічого неможливого.
Стародавні греки першими навчилися визначати відстань до кораблів в морі або до іншого недоступного предмета. Ознаки рівності трикутників здавна мали важливе значення в геометрії, оскільки доведення багатьох теорем зводиться до доведення рівності тих чи інших трикутників. Доведенням рівності трикутників займалися піфагорійці.
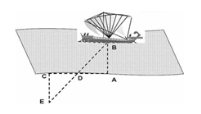
Фалесу Мілетському приписують доведення ІІ ознаки рівності трикутників. Цю теорему Фалес використав для визначення відстані від берега до кораблів у морі. Яким способом користувався при цьому Фалес точно не відомо. Припускають, що його спосіб полягав в наступному:
|
Нехай A – точка берега, B – корабель у морі. Для визначення відстані AB прокладають на березі перпендикуляр АС довільної довжини ACAB. Знаходять середину цієї відстані АС і вкапують палку. Нехай це точка О. Тоді отримають рівні відрізки СО=ОА. У точці С знов побудували прямий кут, причому спостерігач має йти перпендикуляром доти, доки не дійде до точки Е, з якої корабель В і точку О буде видно так, ніби вони лежать на одній прямій. Тоді CE дорівнюватиме шуканій відстані AB. Доведення ґрунтується на ІІ ознаці рівності трикутників. ОC=ОA за побудовою; С=A=900 за побудовою; EОС=BОA як вертикальні. |
|
Можна привести багато різних прикладів задач практичного змісту, аналогічних даній. Я зараз приведу приклади двох подібних задач, які ми з вами розв’яжемо разом.
|
|
|
|
Астролябія – це вимірювальний прилад для кутів, яким до XVIII століття користувались для визначення широти i довготи в астрономії та навігації. Теодоліт – це геодезичний інструмент для визначення напрямів і виміру горизонтальних і вертикальних кутів при геодезичних роботах, топографічних і маркшейдерських зйомках, в будівництві і т. п.
Задача 1. Для знаходження відстані від точки В до дзвіниці А, яка розташована на іншому березі річки, за допомогою рулетки і астролябії або теодоліта позначили на місцевості точки С, D, E, так, що В, С, D лежать на одній прямій, причому точка С є серединою відстані ВD. Потім намічають таку точку Е, з якої дзвіницю А і точку С буде видно так, ніби вони лежать на одній прямій. Отримали пряму АЕ, яка проходить через точку С, причому АВС=СDE. Потім, вимірявши одну із сторін СDЕ, визначили відстань від В до А. Яку сторону виміряли? Відповідь обґрунтуйте.
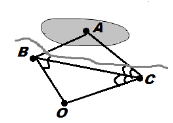
Задача 2. Для визначення ширини озера на його березі позначили точки А і В, а потім ще точки С, D і О так, що точка О – спільна середина відстаней АС і ВD. Як тепер можна визначити ширину озера? Відповідь обґрунтуйте.
Задача 3. Від об’єкта В, розташованого на одному березі річки треба провести телефонний кабель по річному дну до недоступної точки А на острові. Як з’ясувати необхідну довжину кабелю, не перепливаючи річку? Один зі способів, крім вже переглянутих - це такий. Для знаходження відстані від об’єкта В до недоступного об’єкта А вибирають довільну точку С, проводять і вимірюють відстань ВС. За допомогою знов астролябії або теодоліта вимірюють кути, під якими з точок В і С можна побачити недоступний об’єкт А. Потім на березі знаходять таку точку О, яку можна побачити з точок В і С під вже відомими кутами. Доведіть, що ВА=ВО.
Якщо залишився час можна розглянути усно задачі:
1) Відстань від дома до школи 2 км, а від дома до станції 5 км. Чи може відстань від школи до станції бути рівною: а) 2 км; б) 3 км; в) 6 км; г) 8 км? (нерівність трикутника – сума двох менших сторін завжди більше найбільшої сторони. Тоді 2+2<5; 2+3=5; 2+5>6 підходить; 2+5<8)
2) Чи можна побудувати трикутну опалубку даху, якщо у нас є балки довжиною: а) 2 м, 3 м, 4 м; б) 4 м, 3 м, 7 м; в) 6 м, 7 м, 8 м. (нерівність трикутника – сума двох менших сторін завжди більше найбільшої сторони. Тоді 2+3>4 підходить, 6+7>8)
3) Столяру треба закрити отвір трикутної форми. Скільки розмірів і які він повинен зняти, якщо отвір має вигляд рівностороннього або прямокутного трикутника? (одне або два)
Підбиття підсумків уроку
Й Мудрець сказав: «Дві людини, які обмінялись золотими монетами, не стали багатшими, але якщо вони обмінялись думками, то кожний з них стає вдвоє багатшим. Адже обидва стали тепер розумнішими». Обмінюючись думками люди набувають нових знань. Так і ми з вами сьогодні.
Я бажаю вам завжди працювати з радістю і задоволенням.
ознаки рівності закріплення Страница 1


про публікацію авторської розробки
Додати розробку