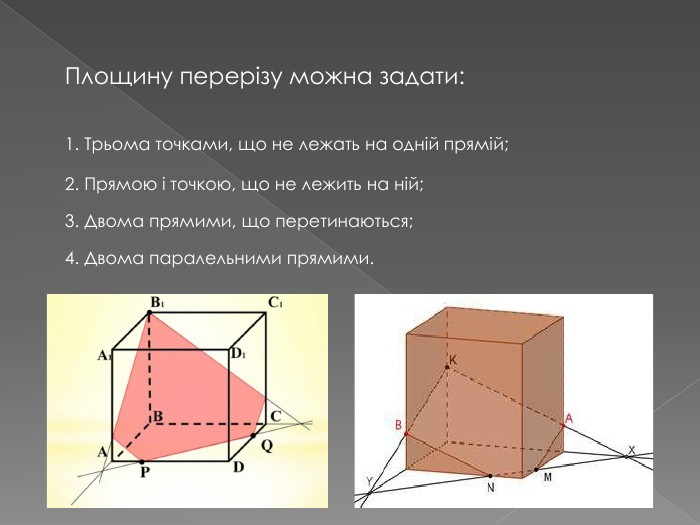
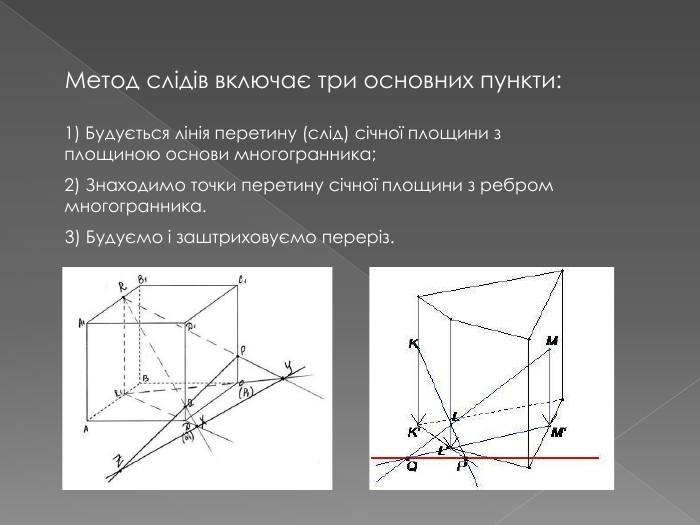
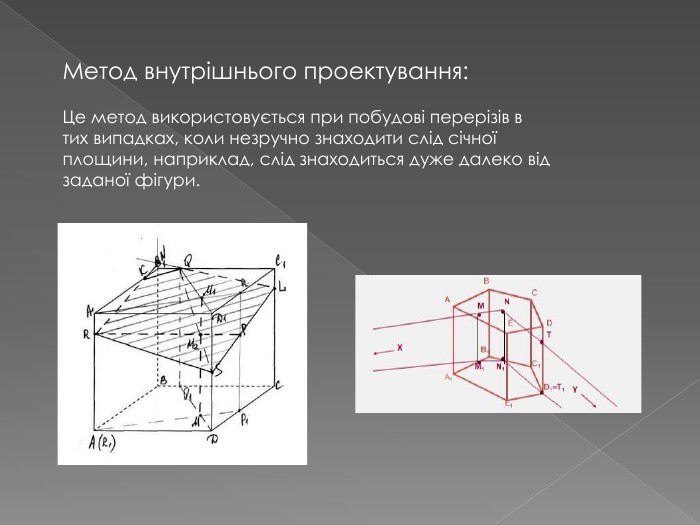
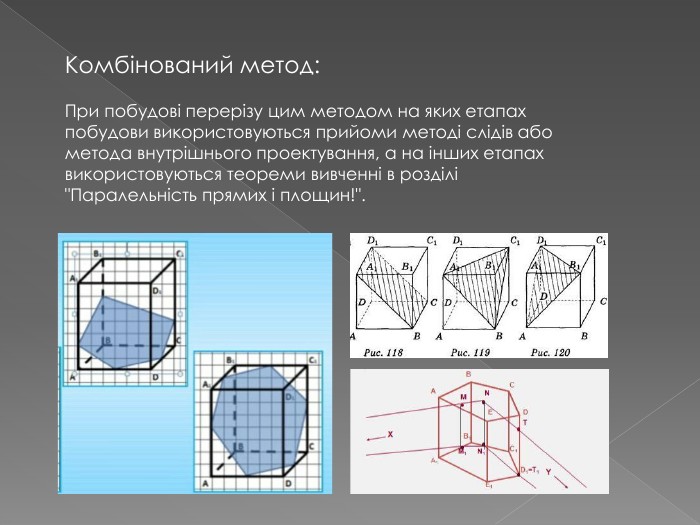
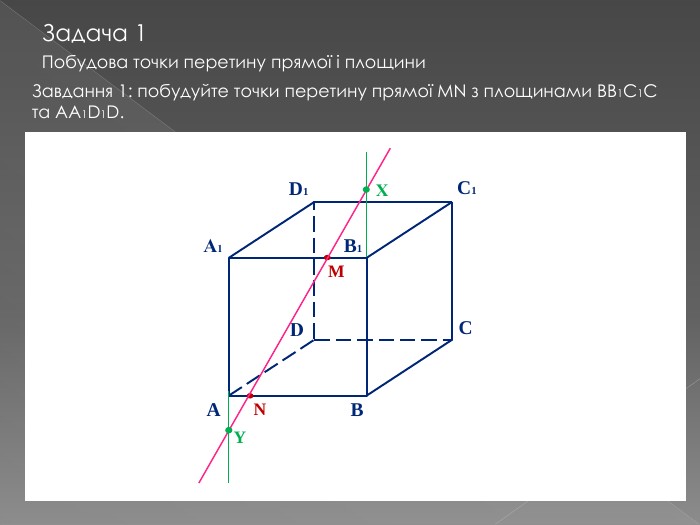
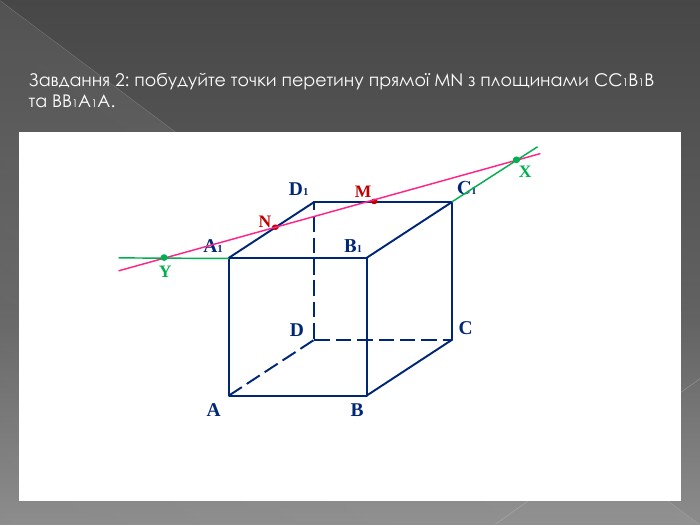
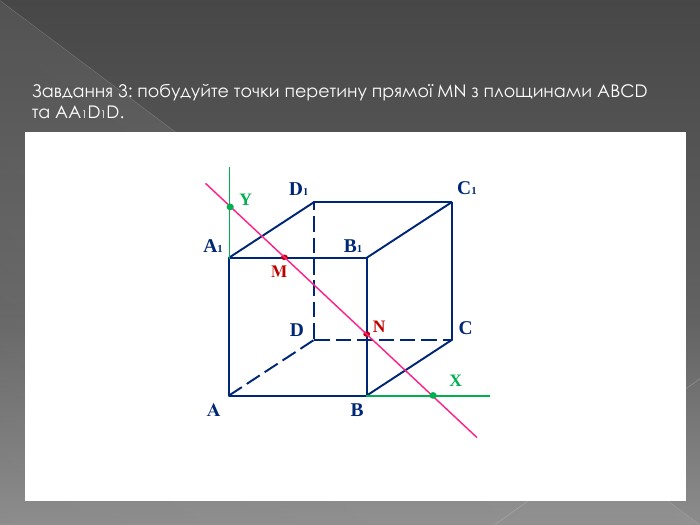
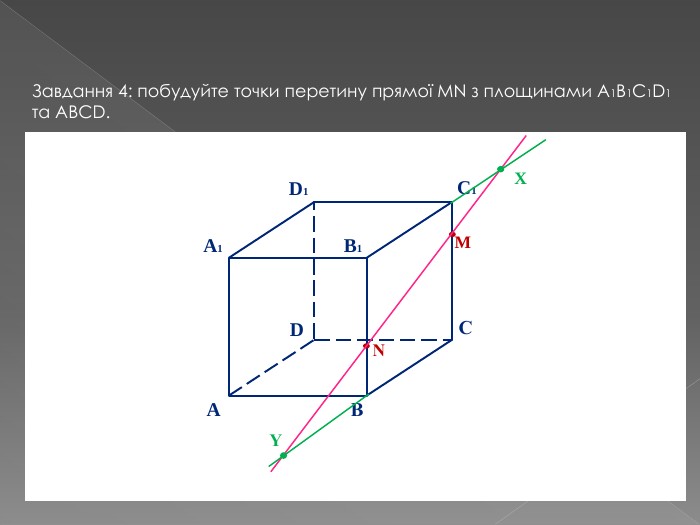
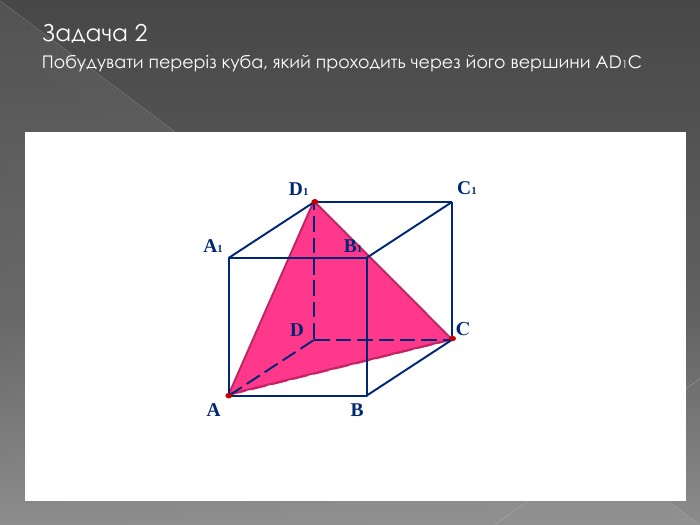
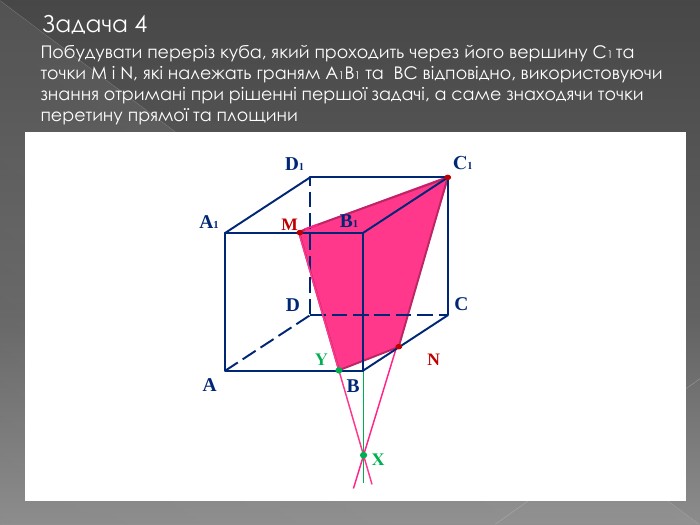
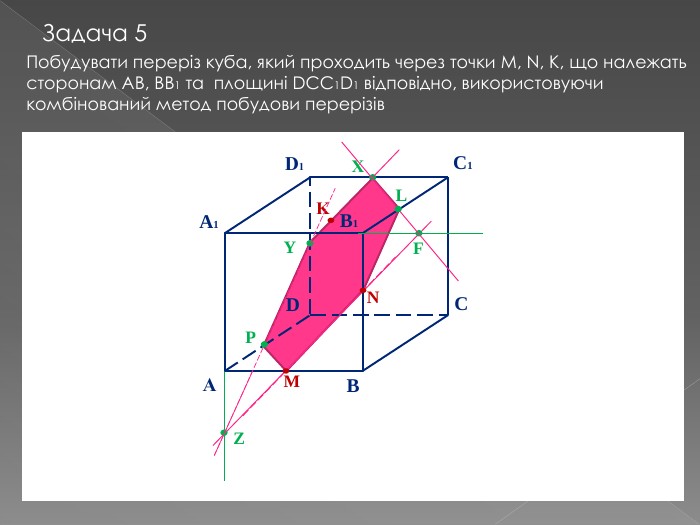
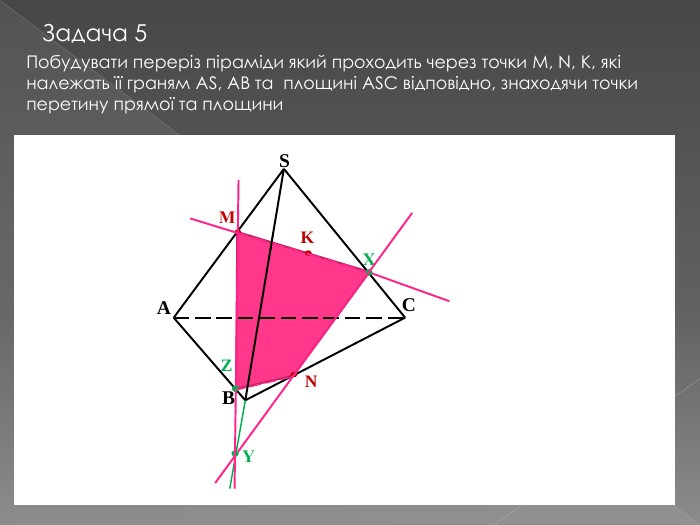
Переріз та побудова перерізів многогранників
Про матеріал
Дана презентація може бути використана для проведення 2-х уроків
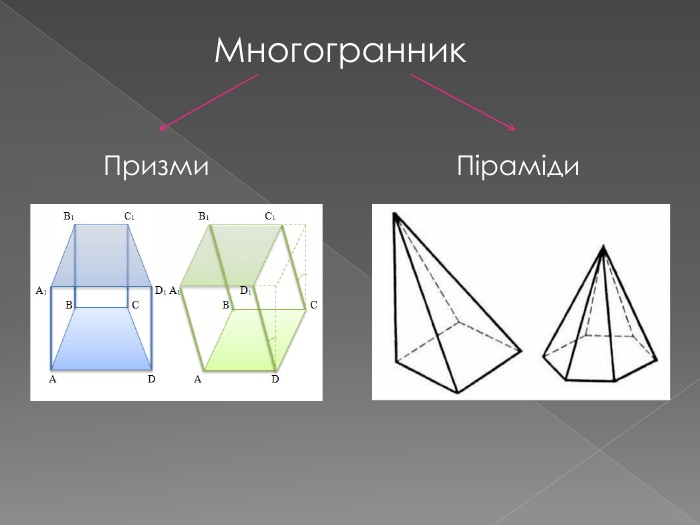
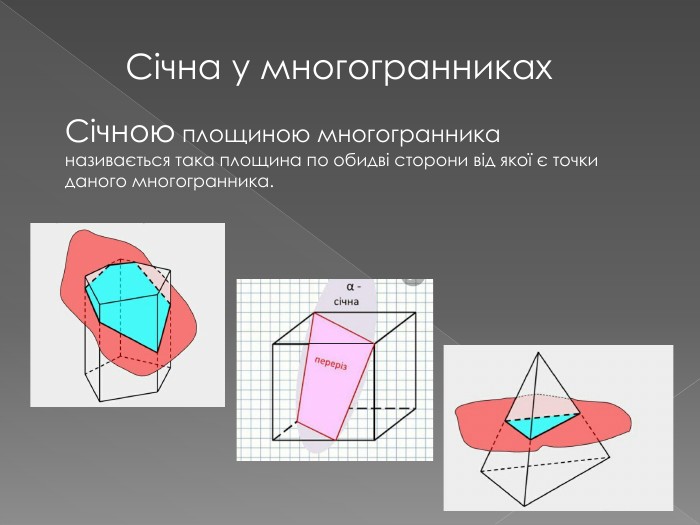
1. многогранники та січна
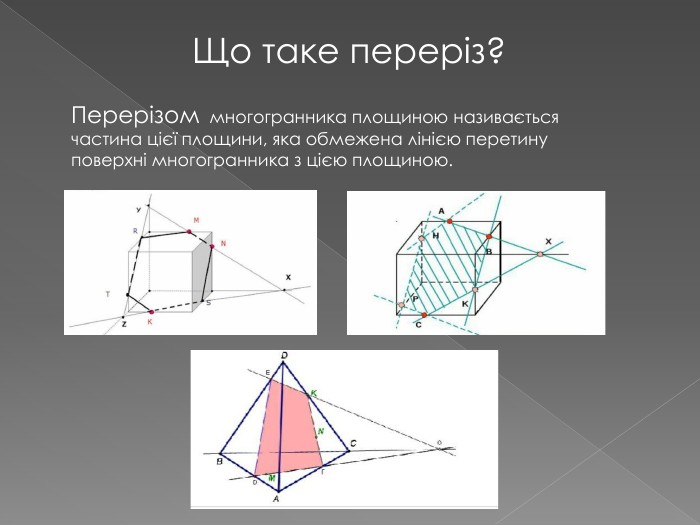
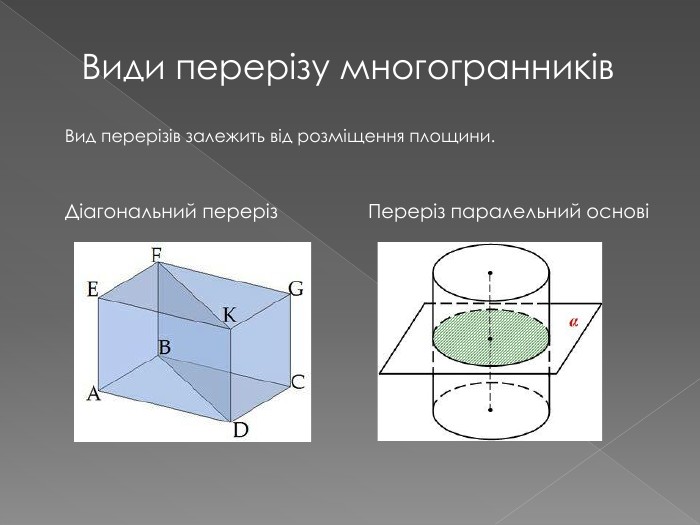
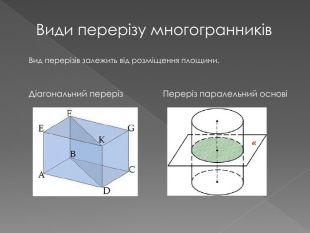
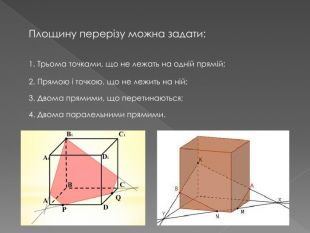
2. побудови перерізів многогранників
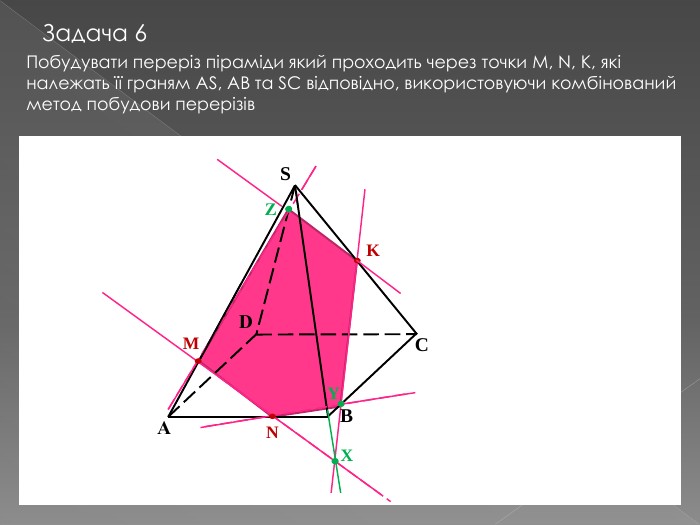
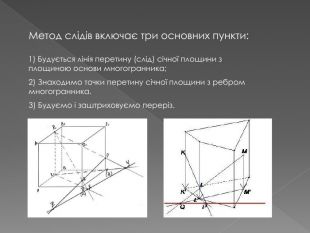
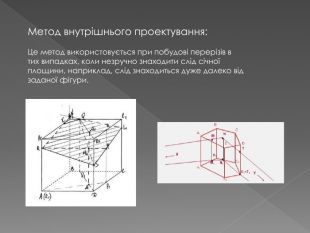
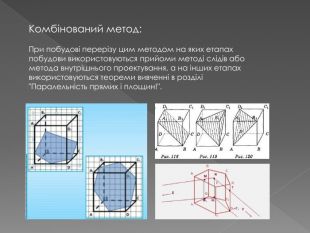
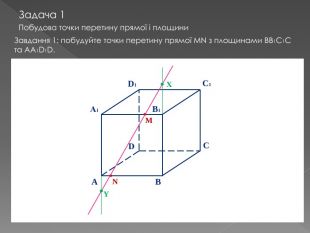
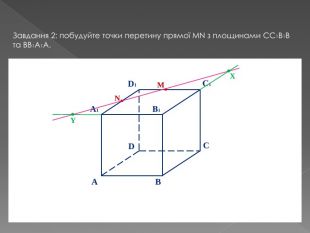
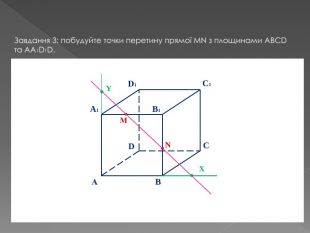
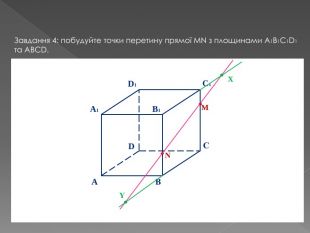
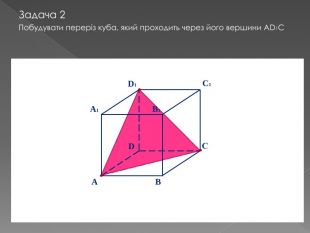
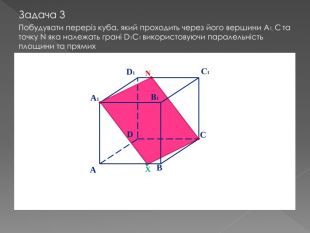
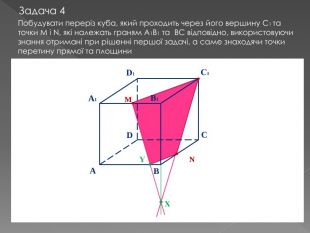
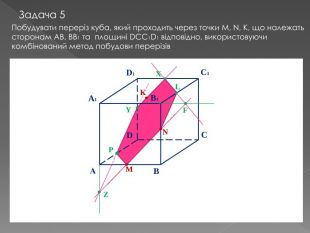
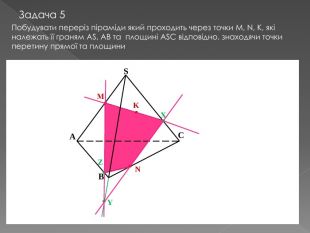
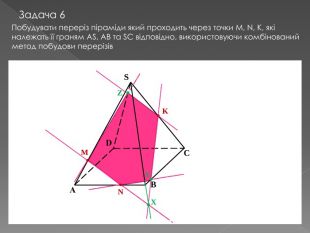
У другій частині презентації, за допомогою анімації, показано як будувати складні перерізи. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку