Перерізи геометричних тіл, що побудовані за клітинками

ГЕОМЕТРІЯ, 11        ТЕМА 4.  МНОГОГРАННИКИ

 

Площа перерізу прямокутного паралелепіпеда

 

                    Кут між прямою і площиною.

 

Тест 2020₁.

34. У прямокутному паралелепіпеді ABCDA₁B₁C₁D₁, через сторону AD нижньої основи й середину ребра B₁C₁ проведено площину . Висота паралелепіпеда дорівнює 18, грань CC₁D₁D є квадратом. Діагональ паралелепіпеда утворює з площиною основи кут .

 

 

 

 

 

 

 

 

Площа перерізу правильної трикутної призми

 

                     Кут між прямою і площиною.

 

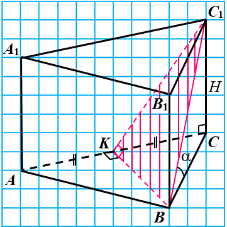Тест 2020_П. 34. Основою правильної трикутної призми ABCA₁B₁C₁ є трикутник ABC. Висота призми дорівнює H, діагональ бічної грані нахилена до площини основи під кутом α. Через висоту BK трикутника ABC та вершину C₁ проведено площину .

 

 

 

 

 

 

 

 

Площа перерізу чотирикутної піраміди

 

                      Перпендикулярність прямої і площини.

                      Кут між площинами.

 

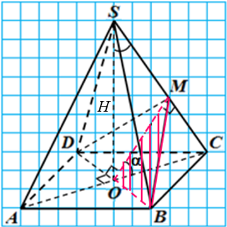Тест 2018₂. 32. У правильній чотирикутній піраміді SABCD через діагональ BD основи перпендикулярно до бічного ребра SC проведено площину . Ця площина утворює з площиною основи кут . Висота піраміди дорівнює Н.

 

 

 

 

 

 

 

 

 

ГЕОМЕТРІЯ, 11         ТЕМА 5.  ТІЛА  ОБЕРТАННЯ

Переріз циліндра площиною, паралельною його осі

 

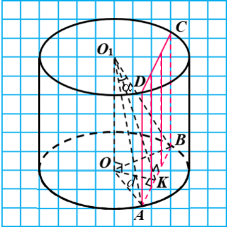Тест 2019₁ 32. У нижній основі циліндра проведено хорду АВ, довжина якої дорівнює с. Цю хорду видно із центра верхньої основи під кутом α. Через хорду АВ проведено площину β паралельно осі циліндра на відстані d (d  0)
від неї.

 

 

 

 

 

 

 

 

 

Переріз конуса площиною, що проходить через його вершину

 

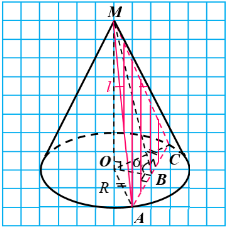Тест 2019₂ 32. У конусі радіус основи дорівнює R, твірна - l.  Через вершину конуса і хорду його основи проведено площину β. Ця площина утворює з площиною основи конуса гострий кут α.

 

 

 

 

 

 

 

 

 

 

Переріз кулі площиною

 

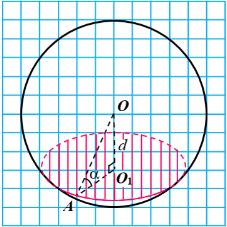Тест 2019_П 32. Площина β проходить через точку А, розташовану на поверхні кулі. Відстань від центра кулі до площини β дорівнює d (d менше радіуса кулі, d ≠ 0). Радіус кулі, проведений у точку А, утворює з площиною β кут .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ГЕОМЕТРІЯ, 11         ТЕМА 6.  ОБ’ЄМИ  ТА  ПЛОЩІ  ПОВЕРХОНЬ  ГЕОМЕТРИЧНИХ ТІЛ

Переріз призми в задачах на об’єм призми

 

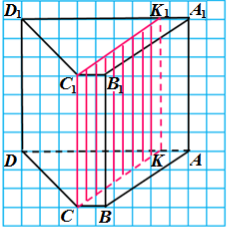Паралельність прямої і площини

Тест 2012₁ 31. Основою прямої призми АВСDА₁В₁С₁D₁ є рівнобічна трапеція АВСD. Через бічне ребро СС₁ призми проведено площину паралельно ребру АВ.

 

 

 

 

 

 

 

 

 

 

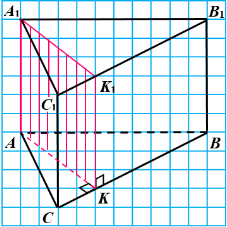Перпендикулярність прямої і площини

Тест 2012₂ 31. Основою прямої трикутної призми АВСА₁В₁С₁ є рівнобедрений трикутник АВС (АВ = ВС). Через її бічне ребро АА₁ проведено площину, перпендикулярну до ребра ВС.

 

 

 

 

 

 

 

 

 

 

Кут між площинами

Тест 2017₂ 32. Основою прямої призми АВСDА₁В₁С₁D₁ є прямокутник АВСD, у якому діагональ АС = а, ВАС = β. Площина, що проходить через вершину верхньої основи і діагональ нижньої основи призми, утворює з площиною основи гострий кут α.  

 

 

 

 

 

 

 

Кут між площинами.

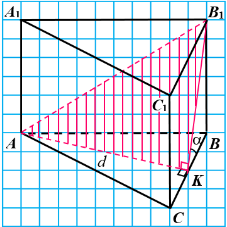Відстань від точки до площини.

Тест 2017₁ 32. Точка K – середина ребра BC правильної трикутної призми ABCA₁B₁C₁. Площина, що проходить через точки A, K та B₁, утворює з площиною основи призми кут α. Відстань від вершини А до грані BB₁C₁C дорівнює d.