Перерізи конуса площинами

Тема: Перерізи конуса площинами. Зрізаний конус

Мета уроку: Навчальна: розглянути основні види перерізів конуса — переріз, перпендикулярний до осі; переріз, що проходить через дві твірні; формування поняття зрізаного конуса та його елементів; сформувати вміння розв’язувати задачі, зо передбачають використання цих понять та властивостивостей. Розвиваюча: Розвивати в учнів правильне уявлення про місце математики в житті, на практиці, зв’язок з іншими предметами. Виховна: виховувати наполегливість, самостійність, культуру спілкування старшокласників, зацікавленість за своєї професіїТип уроку: урок засвоєння нових знань, формування вмінь. Вид уроку: урок з елементами гри .

«Знання – найпрекрасніше з володінь. Всі прагнуть до нього, саме ж воно не приходить»Абу-р-Райхан ал-Біруні, арабский математик.

Нас оточує багато предметів конічної форми. Пригадаємо яке тіло обертання вивчили на попередньому уроці

Туманність Конус

Конуси (Conus), мабуть, найбагатша видами (вже відомо понад 550 видів і щорічно описують не менше дюжини нових) рід морських тварин з класу черевоногих молюсків, або равликів

Вулкани. Конусоподібна форма

КОНУС в перекладі з давньогрецької «соснова шишка»

Аполон Пергський написав великий трактат про конічні перетини. Він був учнем Евкліда (III ст. До н. Е.). Евклід створив великий труд з 15 книг під назвою «Начала». Ці книги видаються і в даний час, а в школах Англії по ним вчаться досі.

Відскануйте QR-код. Пройдіть тест. Максимальна оцінка за тест – 7 балів

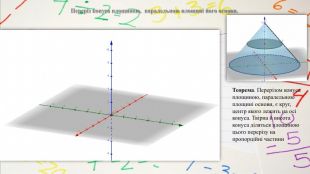
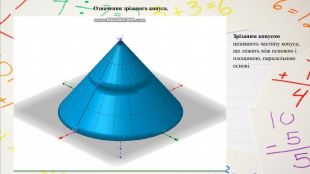
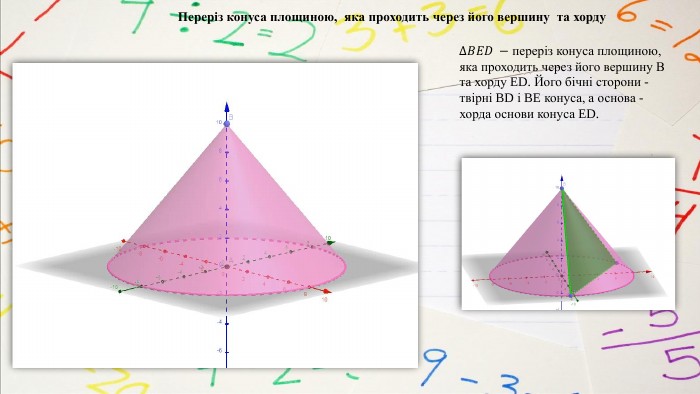
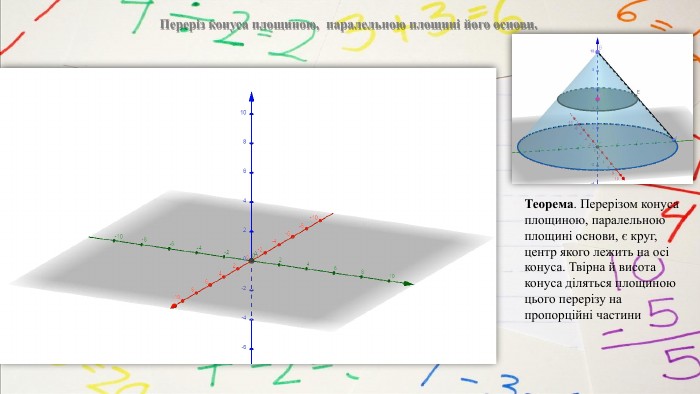
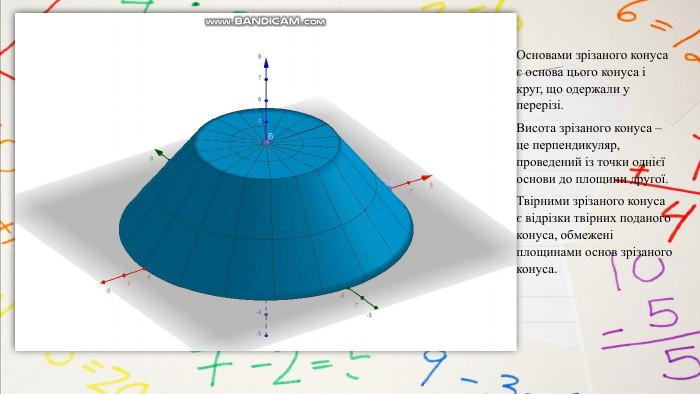
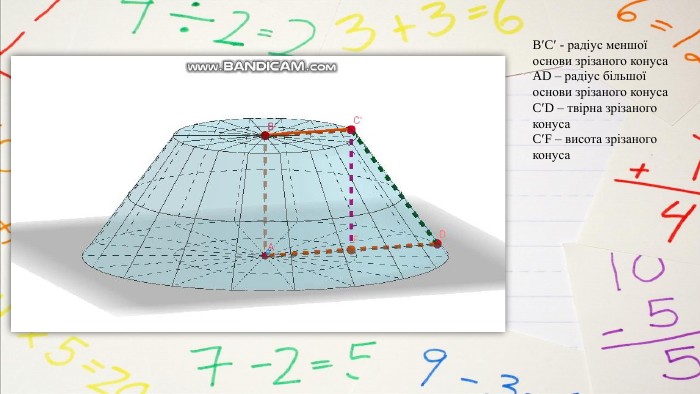
План вивчення теми. Переріз конуса площиною, яка проходить через його вершину та хорду. Переріз конуса площиною, паралельною площині його основи. Означення зрізаного конуса. Елементи зрізаного конуса. Зрізаний конус як тіло обертання прямокутної трапеції навколо меншої бічної сторони. Осьовий переріз зрізаного конуса. Властивості зрізаного конуса. Конічні поверхні як джерело кривих другого порядку

Переріз конуса площиною, яка проходить через його вершину та хорду∆𝐵𝐸𝐷 − переріз конуса площиною, яка проходить через його вершину В та хорду ED. Його бічні сторони - твірні BD і BE конуса, а основа - хорда основи конуса ED.

Переріз конуса площиною, паралельною площині його основи. Теорема. Перерізом конуса площиною, паралельною площині основи, є круг, центр якого лежить на осі конуса. Твірна й висота конуса діляться площиною цього перерізу на пропорційні частини

Означення зрізаного конуса. Зрізаним конусом називають частину конуса, що лежить між основою і площиною, паралельною основі.

Основами зрізаного конуса є основа цього конуса і круг, що одержали у перерізі. Висота зрізаного конуса – це перпендикуляр, проведений із точки однієї основи до площини другої. Твірними зрізаного конуса є відрізки твірних поданого конуса, обмежені площинами основ зрізаного конуса.

BC - радіус меншої основи зрізаного конуса. AD – радіус більшої основи зрізаного конуса. CD – твірна зрізаного конуса. CF – висота зрізаного конуса

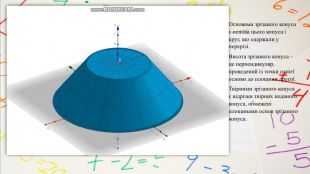
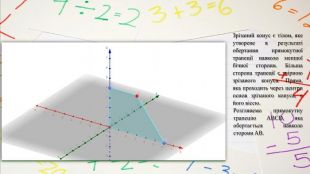
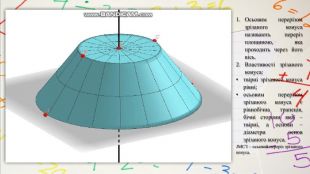
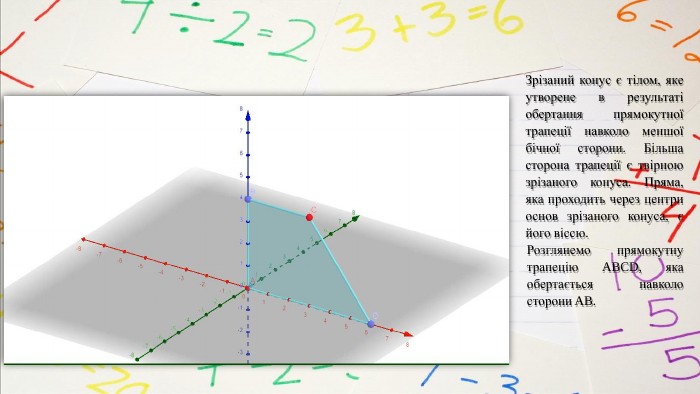
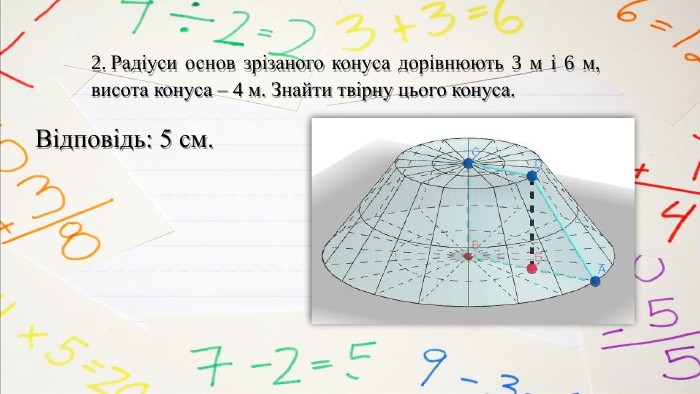
Зрізаний конус є тілом, яке утворене в результаті обертання прямокутної трапеції навколо меншої бічної сторони. Більша сторона трапеції є твірною зрізаного конуса. Пряма, яка проходить через центри основ зрізаного конуса, є його віссю. Розглянемо прямокутну трапецію ABCD, яка обертається навколо сторони AB.

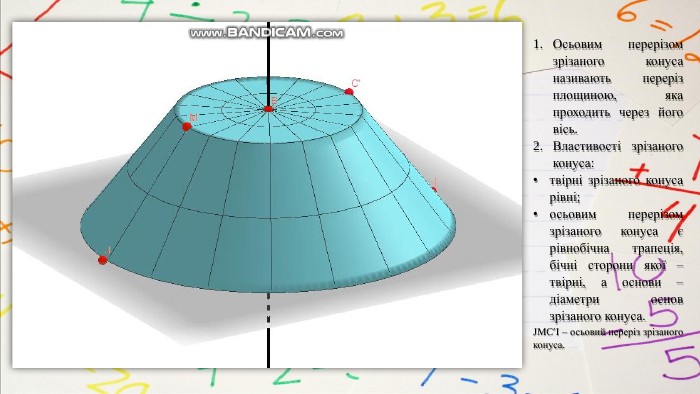
Осьовим перерізом зрізаного конуса називають переріз площиною, яка проходить через його вісь. Властивості зрізаного конуса:твірні зрізаного конуса рівні;осьовим перерізом зрізаного конуса є рівнобічна трапеція, бічні сторони якої – твірні, а основи – діаметри основ зрізаного конуса. JMCI – осьовий переріз зрізаного конуса.

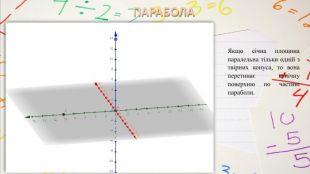
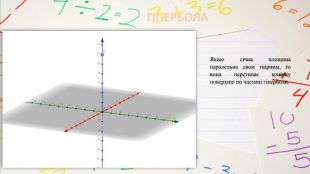
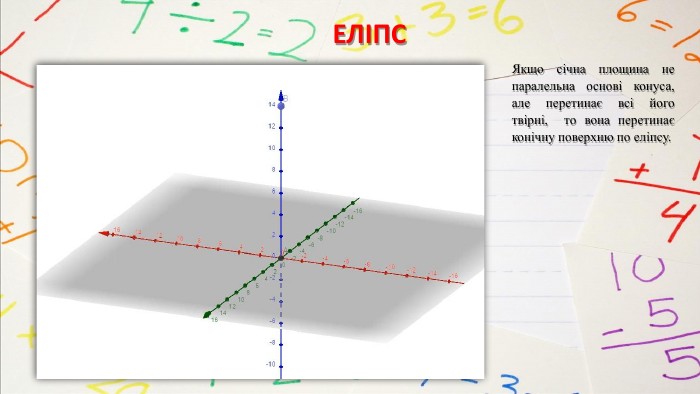
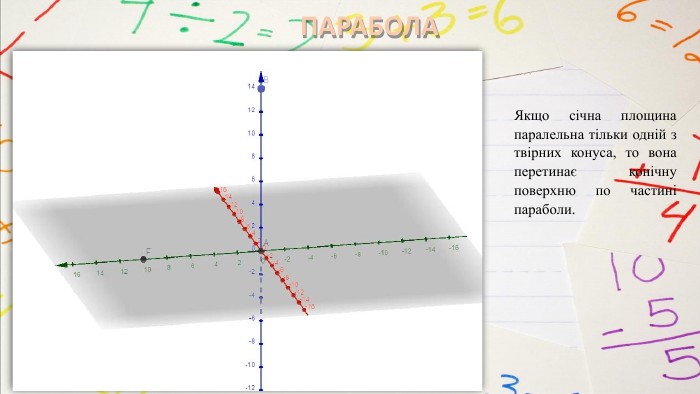
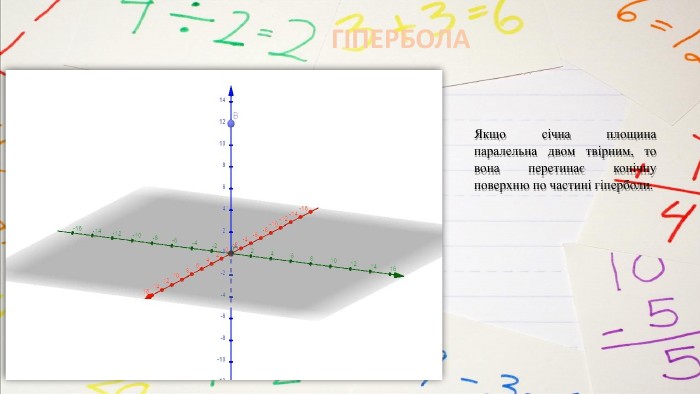
КОНІЧНІ ПОВЕРХНІ ЯК ДЖЕРЕЛО КРИВИХ ДРУГОГО ПОРЯДКУВище розглянули конічні перерізи, які або паралельні основі конуса, або проходять через його вершину. А якщо проводити січну площину інакше? Виявляється, що можна отримати еліпс, параболу, гіперболу. Одним з перших, хто почав вивчати ці криві, був учень знаменитого Платона, давньогрецький математик Менехм (IV ст. до н. е.). змінюючи кут при вершині прямого кругового конуса, Менехм отримав три види кривих: еліпс – якщо кут при вершині конуса гострий; параболу – якщо кут прямий; одну гілку гіперболи – якщо тупий. Їх запропонував один із найвизначніших геометрів давнини Аполлоній Пергський (262-190 до н.е.), який присвятив чудовим кривим трактат з восьми книг «Конічні перерізи». Аполлоній показав, що еліпс, параболу, гіперболу можна отримати, проводячи різні перерізи одного й того самого конуса.

Якщо січна площина не паралельна основі конуса, але перетинає всі його твірні, то вона перетинає конічну поверхню по еліпсу. ЕЛІПС

Якщо січна площина паралельна тільки одній з твірних конуса, то вона перетинає конічну поверхню по частині параболи. ПАРАБОЛА

Якщо січна площина паралельна двом твірним, то вона перетинає конічну поверхню по частині гіперболи. ГІПЕРБОЛА

ВИКОНАННЯ УСНИХ ВПРАВЧерез середину висоти конуса проведено площину, паралельну його основі. Чому дорівнює відношення площі утвореного перерізу до площини основи конуса?Відповідь: 0,5 Sосн

2. Радіуси основ зрізаного конуса дорівнюють 3 м і 6 м, висота конуса – 4 м. Знайти твірну цього конуса. Відповідь: 5 см.

ВИКОНАННЯ ПИСЬМОВИХ ВПРАВВисота конуса дорівнює 18 см, а радіус основи – 6 см. Площина, перпендикулярна до осі конуса, перетинає його бічну поверхню по колу, радіус якого 4 см. Знати відстань від площини перерізу до площини основи конуса.(бажаючі учні можуть записати розв'язок задачі на вільному місці слайду використовуючи комунікаційне програмне забезпечення Zoom)Розв'язанняDBA⁓EBC; 𝐸𝐶𝐷𝐴=𝐵𝐶𝐵𝐴 . BC= 𝐸𝐶∗𝐵𝐴𝐷𝐴=4∗186=12 см. AC= BA-BC=18-12= 6 см. Відповідь: АС= 6 см.

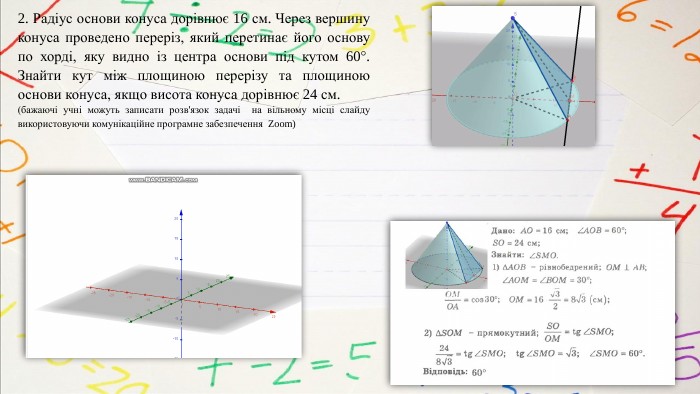
2. Радіус основи конуса дорівнює 16 см. Через вершину конуса проведено переріз, який перетинає його основу по хорді, яку видно із центра основи під кутом 60. Знайти кут між площиною перерізу та площиною основи конуса, якщо висота конуса дорівнює 24 см.(бажаючі учні можуть записати розв'язок задачі на вільному місці слайду використовуючи комунікаційне програмне забезпечення Zoom)

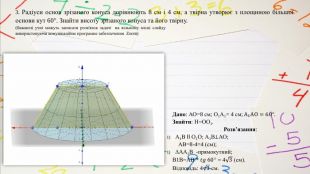
3. Радіуси основ зрізаного конуса дорівнюють 8 см і 4 см, а твірна утворює з площиною більшої основи кут 60. Знайти висоту зрізаного конуса та його твірну. Дано: АО=8 см; О1 А1= 4 см; А1 АО=60. Знайти: Н=ОО1. Розв’язання: А1 В ІІ О1 О; А1 В⊥АО;АВ=8-4=4 (см);АА1 В -прямокутний;В1 В=АВ * 𝑡𝑔 60 = 43 (см). Відповідь: 43 см.(бажаючі учні можуть записати розв'язок задачі на вільному місці слайду використовуючи комунікаційне програмне забезпечення Zoom)

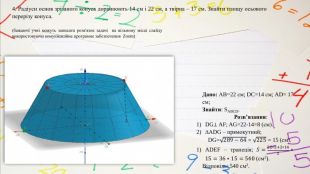
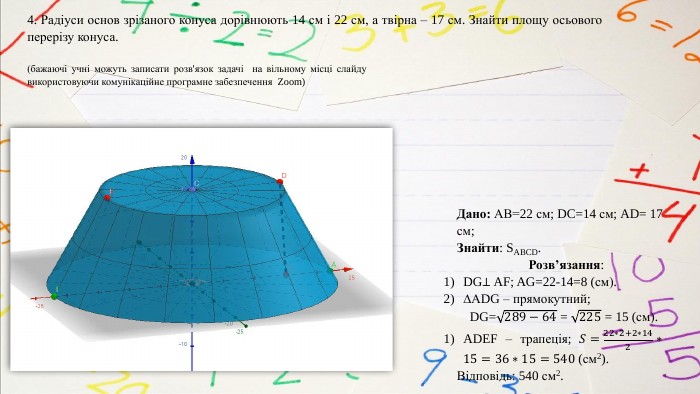
Дано: АВ=22 см; DC=14 см; AD= 17 см;Знайти: SABCD. Розв’язання: DG⊥ AF; AG=22-14=8 (см). АDG – прямокутний; DG=289−64 = 225 = 15 (см). ADEF – трапеція; 𝑆=22∗2+2∗142∗15=36∗15=540 (см2). Відповідь: 540 см2.4. Радіуси основ зрізаного конуса дорівнюють 14 см і 22 см, а твірна – 17 см. Знайти площу осьового перерізу конуса.(бажаючі учні можуть записати розв'язок задачі на вільному місці слайду використовуючи комунікаційне програмне забезпечення Zoom)

Відскануйте QR-код. Пройдіть тест. Максимальна оцінка за тест – 5 балів (в сумі з попереднім тестом – 12 балів)

ЯКЕ ІЗ ЗОБРАЖЕНИХ ТІЛ Є КОНУСОМ?

Яке слово закодоване в кросворді?ХТО ПЕРШИЙ?Відскануйте

Домашнє завдання1. Опрацювати §20 стор. 1282. №№ 20.5 (2), 20.10 .3. Дати відповіді на питання кросворду (знайти ключове слово).4. Дати відповідь на питання: «Чому пожежні відра мають форму конуса?».