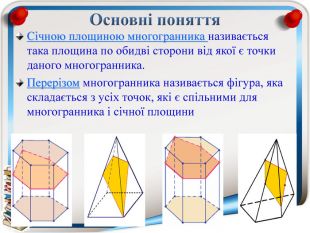
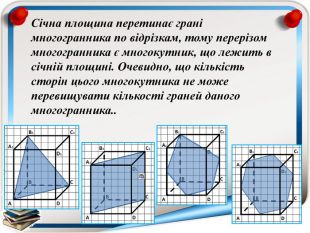
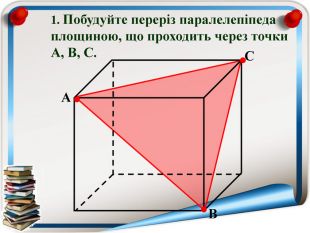
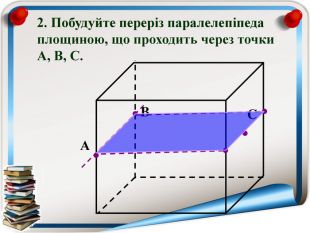
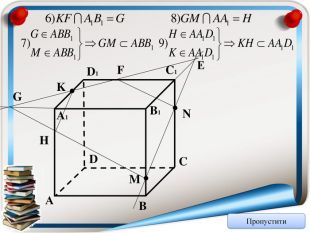
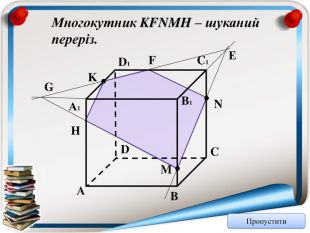
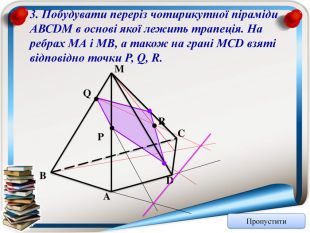
Перерізи многогранників (презентація)

Виконала: Радченко Наталія

Повторити геометричні поняття і твердження; навчитися будувати перерізи різними способами; розвивати просторове уявлення та вміння логічно вибудовувати своє пояснення. Виховувати інтерес до технічних знань.

Якщо дві точки прямої лежать на одній площині, то і вся пряма належить даній площині.

Якщо дві паралельні площини перетинаються третьою площиною, то лінії їх перетину паралельні.

Січною площиною многогранника називається така площина по обидві сторони від якої є точки даного многогранника. Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини

Січна площина перетинає грані многогранника по відрізкам, тому перерізом многогранника є многокутник, що лежить в січній площині. Очевидно, що кількість сторін цього многокутника не може перевищувати кількості граней даного многогранника..

Що означає побудувати переріз? Побудувати переріз многогранника площиною – означає: в площині кожної перетнутої грані вказати дві точки, що належать перерізу; з'єднати ці точки прямою; знайти точки перетину прямої з ребрами многогранника.

1. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С. А В С

2. Побудуйте переріз паралелепіпеда площиною, що проходить через точки А, В, С. C B А

Метод слідів. Метод внутрішнього проектування або метод допоміжних перерізів Комбінований метод

Якщо площина α перетинає площину β по прямій т, то пряму т називають слідом площини α на площину β. α β т

Метод слідів включає три важливих пункти: Будується лінія перетину (слід) січної площини з площиною основи многогранника. Знаходимо точки перетину січної площини з ребром многогранника. Будуємо і заштриховуємо переріз. М C B А К Р

1. Побудуйте переріз піраміди АВСD площиною, що проходить через внутрішні точки M, N, P ребер AD, DC відповідно, і площини АВС. А N М Р D С В

А N М Р D С В K H G 8) MNGH. Пропустити

2. Побудувати переріз куба АВСDА1В1С1D1 площиною, що проходить через внутрішні точки M, N, K ребер BB1, CC1, A1D1 відповідно А C B D А1 D1 C1 B1 K N M Пропустити

А C B D А1 D1 C1 B1 K N M Е Пропустити

А C B D А1 D1 C1 B1 K N M Е F Пропустити

А C B D А1 D1 C1 B1 K N M Е F G H Пропустити

А C B D А1 D1 C1 B1 K N M Е F G H Многокутник KFNMH – шуканий переріз. Пропустити

3. Побудувати переріз чотирикутної піраміди АВСDM в основі якої лежить трапеція. На ребрах МА і МВ, а також на грані МСD взяті відповідно точки Р, Q, R. B A C D Q M R P Пропустити

M X Y A A1 N M1 N1 T D1=T1 B C D E E1 C1 B1 Цей метод використовується при побудові перерізів в тих випадках, коли незручно знаходити слід січної площини, наприклад, слід знаходиться дуже далеко від заданої фігури

що проходить через точки M, N, Р. Побудова перерізу п'ятикутної призми площиною, Пропустити

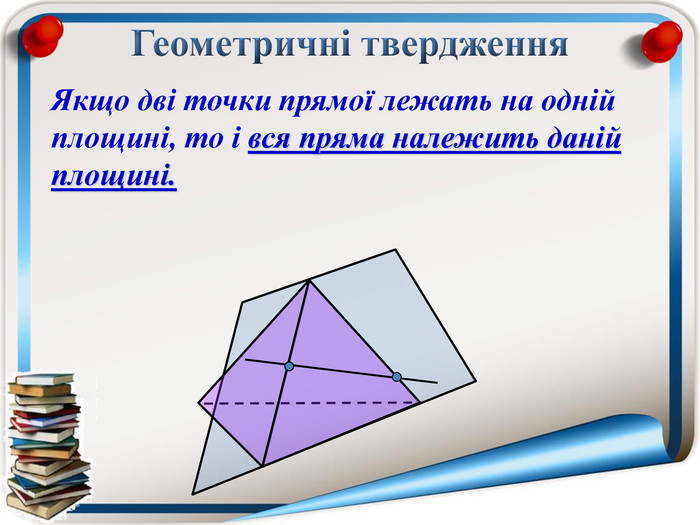
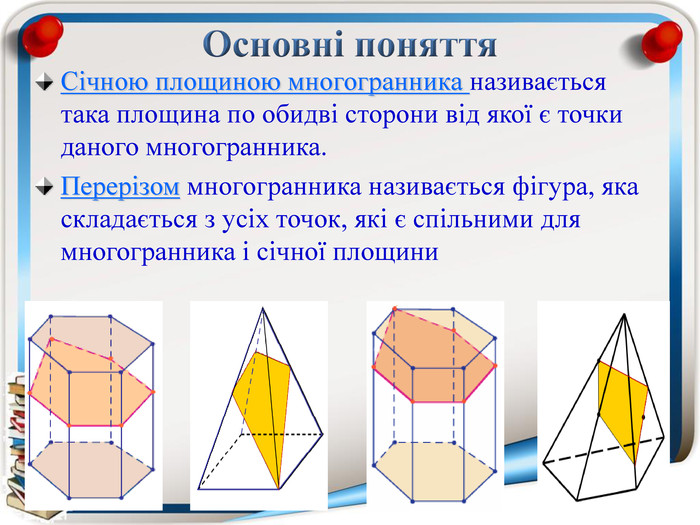
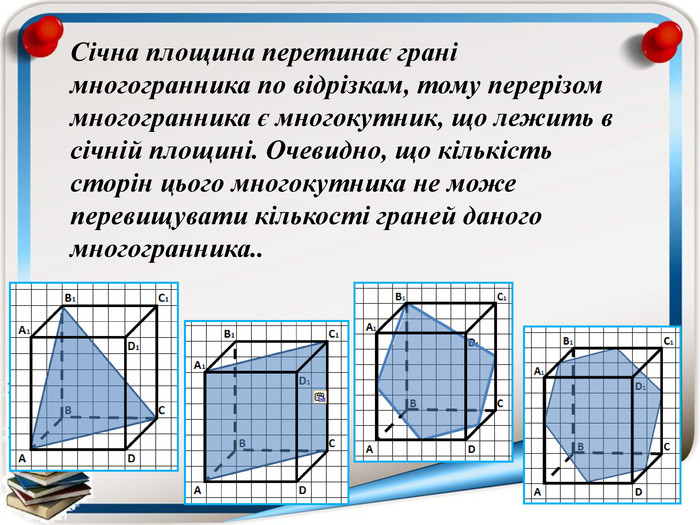
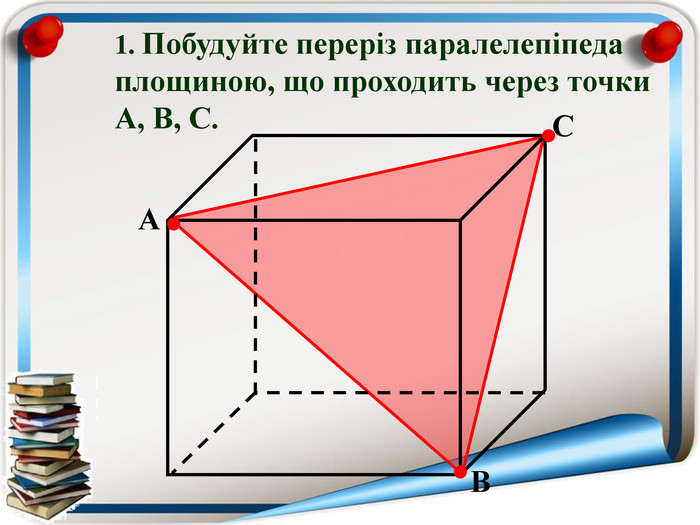
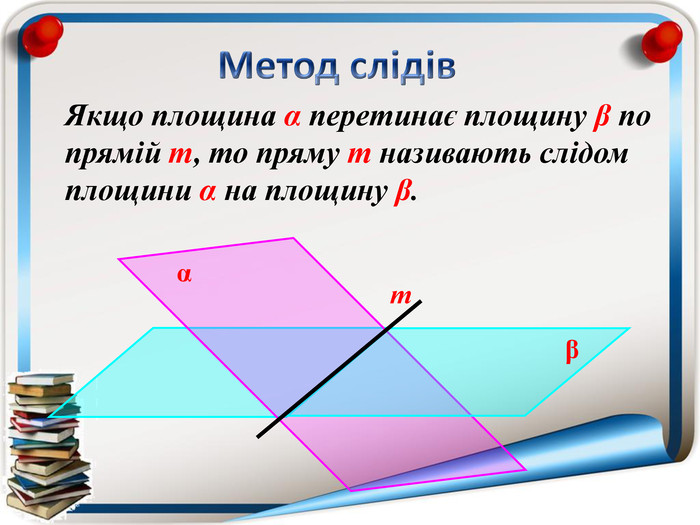
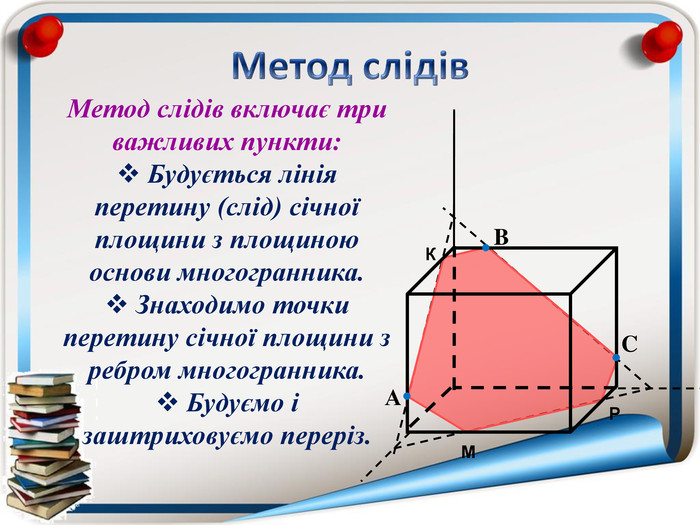
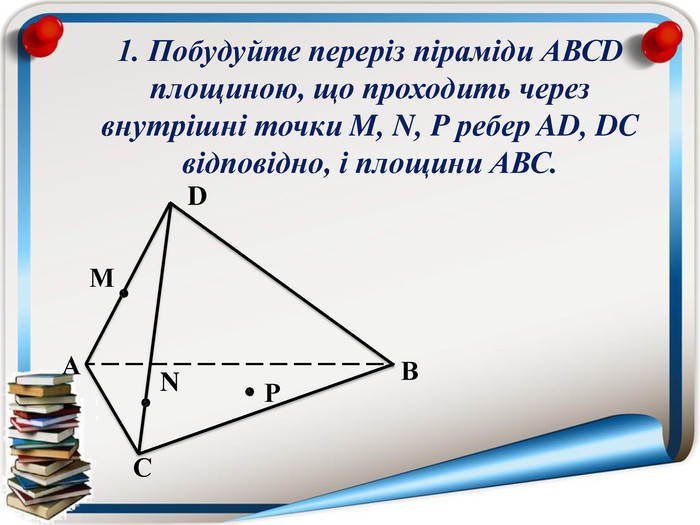
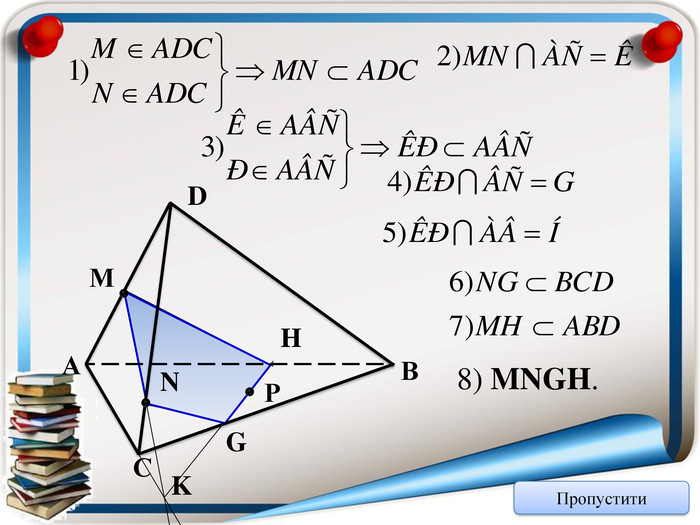
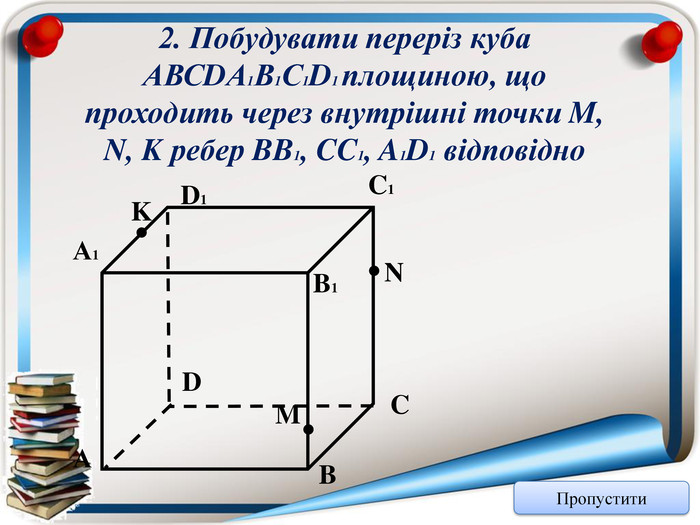
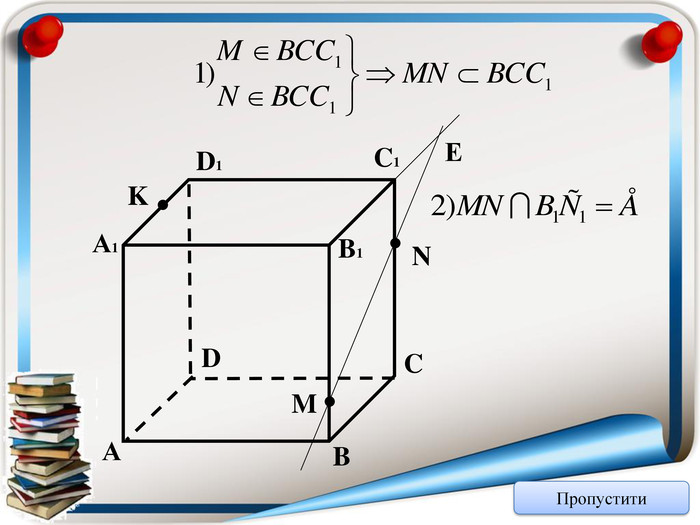
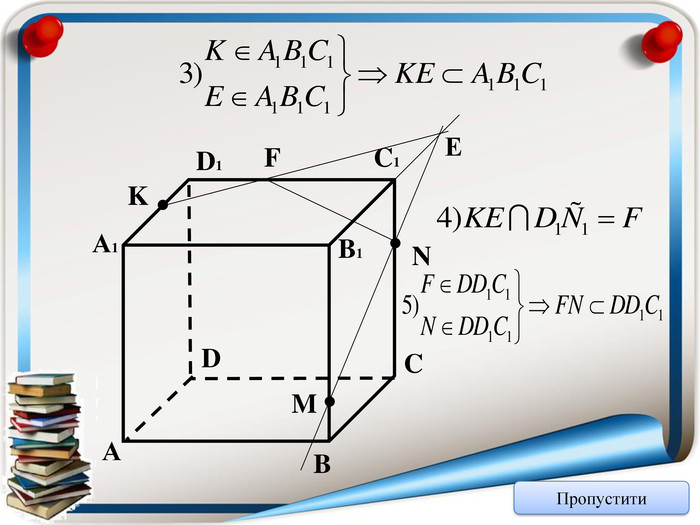
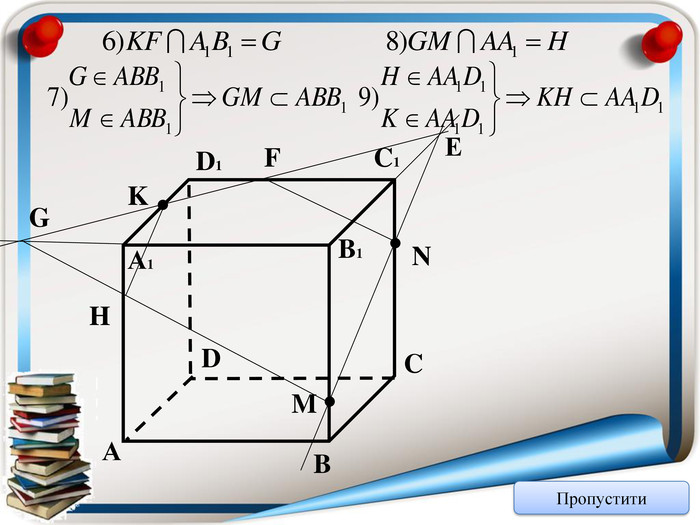
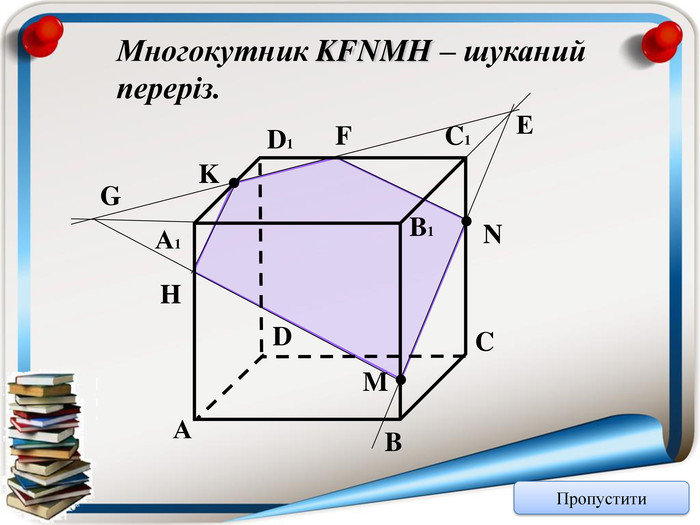
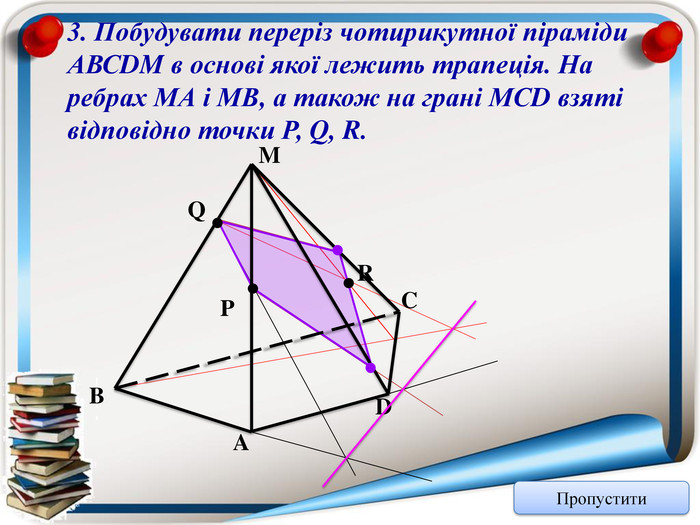
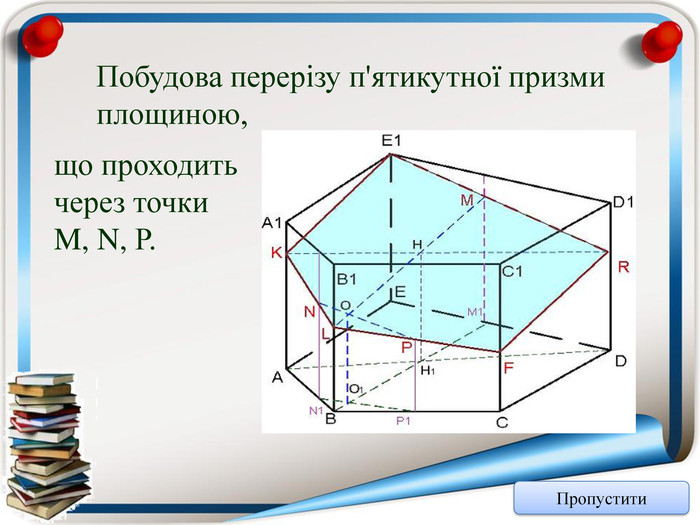
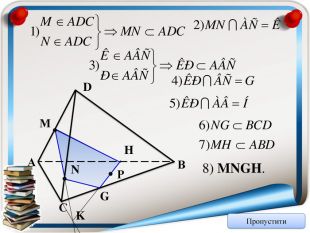
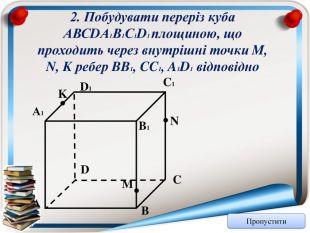
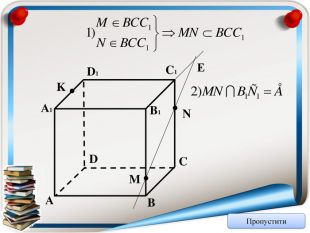
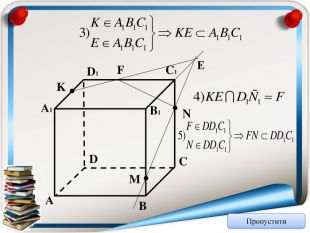
Аксіома 1. Через будь-які три точки, що не лежать на одній прямій можна провести площину і до того ж тільки одну; Аксіома 2. Якщо дві точки прямої належать площині, то всі точки даної прямої належать площині; Аксіома 3. Якщо дві площини мають спільну точку, то вони мають спільну пряму на якій лежать спільні точки цих площин; Теорема (ознака паралельності двох площин). Якщо дві прямі, що перетинаються однієї площини відповідно паралельні двом прямим, що перетинаються іншої площини, то ці площини паралельні; Теорема (властивість паралельних площин). Якщо дві паралельні площини перетнуто третьою, то лінії їх перетину паралельні; Теорема (ознака паралельності прямої і площини). Якщо пряма, що не належить даній площині, паралельна будь-які прямій цієї площини, то вона паралельна і даній площині. Тест