Перетворення цілих виразів
Тема. Перетворення цілих виразів
Мета: перевірити рівень засвоєння знань та вмінь, передбачених Програмою математики з даної теми.
Тип уроку: контроль знань, умінь, навичок.
Хід уроку
І. Організаційний момент
Учитель перевіряє готовність учнів до уроку, фіксує прізвища відсутніх учнів. Повідомляє учням мету уроку та умови виконання завдань тематичної контрольної роботи.
II. Умова завдань тематичної контрольної роботи
|
Варіант 1 |
Варіант 2 |
|
№ 1. Розкладіть на множники: 1) х3 – 9х; 2) 12 – 75с2; 3) -п2 – 8п – 16; 4) 4т3 – 32с3; 5) 3тп + 24п – 9т – 72. |
№ 1. Розкладіть на множники: 1) а3 – 16а; 2) 10х2 – 50; 3) -т2 + 6т – 9; 4) 2п3 + 54k3; 5) ас4 – с4 + ас3 – с2. |
|
№ 2. Розв'яжіть рівняння: 1) 2х3 – 50х = 0; 2) 9х3 + 6х2 + х = 0. |
№ 2. Розв'яжіть рівняння: 1) 6х3 – 24х = 0; 2) 25х3 – 10х2 + х = 0. |
|
№ 3. Розкладіть на множники: 1) а + b + а2 – b2; 2) х2 – 2ху + у2 – т2; 3) (2т – 3)2 – (т + 2)2. |
№ 3. Розкладіть на множники: 1) х2 – у2 + х – у; 2) х2 – 4ху + 4у2 – 1; 3) (4т – 3)2 – (т + 2)2. |
|
№ 4. Доведіть, що:
1) при кожному цілому к значення ви- 2) значення виразу 825 – 6412 ділиться на 7. |
№ 4. Доведіть, що:
1) при будь-якому цілому л значення 2) 220 + 225 – 411 ділиться на 29. |
|
№ 5. Знайдіть найменше значення виразу: 1) х2 + 8х + 16; 2) х2 + 8х + 17. При яких значеннях х вираз набуває найменшого значення? |
№ 5. Знайдіть найменше значення виразу: 1) x2 – 6х + 9; 2) x2 – 6x + 12. При яких значеннях х вираз набуває найменшого значення? |
|
№ 6. Доведіть, що різниця квадратів двох послідовних цілих чисел є непарним числом |
№ 6. Доведіть, що різниця квадратів двох цілих чисел, взятих через 1, ділиться на 4 |
III. Розв'язання та відповіді до завдань тематичної контрольної роботи
|
Варіант 1 |
Варіант 2 |
|
№1. 1) х(х – 3)(х + 3); 2) 3(4 – 25с2) = 3(2 – 5с)(2 + 5с); 3) -(п2 + 8п + 16) = -(п + 4)2; 4) 4(т3 – 8с3) = = 4(т – 2с)(т2 + 2ст + 4с2); 5) 3(тп + 8п – 3т – 24) = = 3(т(п – 3) + 8(п – 3)) = 3(п – 3)(т + 8). |
№ 1. 1) а(а2 – 16) = а(а – 4)(а + 4); 2) 2(9х2 – 25) = 2(3х – 5)(3х + 5); 3) -(т2 – 6т + 9) = -(т – 3)2; 4) 2(п3 + 27k3) = = 2(п + 3k)(п2 – 2kп + 9k2); 5) с2(ас2 – с2 + а – 1) = = с2(с2(а – 1) + (а –1)) = с2(а – 1)(с2 + 1). |
|
№2. 1) 2х(х – 5)(х + 5) = 0; х = 0 або х = 5 або х = -5;
2) х(3х + 1)2 = 0; х = 0 або х = - |
№2. 1) 6х(х2 – 4) = 0; 6х(х – 2)(х + 2) = 0; х = 0 або х = 2, або х = -2; 2) х(25х2 – 10х + 1) = 0;
х(5х – 1) = 0; х = 0 або х = |
|
№3.1) (а + b) + (а + b)(а – b) = = (а + b)(1 + а – b); 2) (x – у)2 – m2 = (х – у – т)(х – у + т); 3) ((2т – 3) – 2(т + 2))(2т – 3 + т + 2)= = (т – 5)(3т – 1). |
№3. 1)(х – у)(х + у) + (х – у) = = (х – у)(х + у + 1); 2) (х – 2у)2 – 1 = (х – 2у – 1)(х – 2у + 1); 3) (4m – 3 – (m + 2))(4m – 3 + m + 2) = = (3т – 5)(5т – 1). |
|
№4. 1) k 3 + 5k2 – k2 – 5k + k + + 5 – k3 – 4k2 – 4k + 3 = = -8k + 8 = 8(-k + 1) ділиться на 8;
2) 825 – 6412 = 825 – 824 = 824(8–1) = 824 ∙7 ділиться на 7 |
N° 4. 1) (2п + 3)2 – (2п – 3)(2п + 5) = = 4п2 + 12п + 9 – (4п2 – 6п + 10п – 15) = = 4п2 + 12п + 9 – 4п2 – 4п +15 = = 8п + 24 = 8(п + 3) ділиться на 8; 2) 220 + 225 – 411 = 220 + 225 – 222 = = 220(1 + 25 – 22) = 220(1 + 32 – 4) = = 220 ∙ 29 ділиться на 29 |
|
№5. 1) х2 + 8х + 16 = (х + 4)2 ≥ 0, най менше значення дорівнює 0, при х + 4 = 0, тобто х = -4; 2) х2 + 8х + 17 = (х2 + 8х + 16) + 1 = = (х + 4) +1 ≥ 1, найменше значення дорівнює 1 при (х + 4) = 0, тобто х + 4 = 0, х = -4. |
№ 5. 1) х2 – 6х + 9 = (х – 3)2 ≥ 0, найменше значення дорівнює 0 при х = 3;
2) х2 – 6х + 12 = (х2 – 6х + 9) + 3 = = (х – 3) + 3 ≥ 3, найменше значення дорівнює 3 при х = 3. |
|
№ 6. Нехай менше число х, тоді наступне — (х +1), а різниця квадратів (х + 1)2 – х2 = х2 + 2х + 1 – х2 = 2х + 1 – непарне число (від ділення на 2 дає остачу 1) |
№ 6. Нехай менше число х, тоді число через 1 дорівнює (х + 2), а різниця квадратів (х + 2)2 – х2 = (х + 2 – х)(х + 2 + х) = = 2 ∙ (2х + 2) = 2 ∙ 2 ∙ (х + 1) = 4(х +1) ділиться на 4 |
IV. Підсумки уроку
По виконанні завдань тематичної контрольної роботи учні здають зошити та одержують аркуші з правильними розв'язаннями; учні здійснюють самоперевірку виконаних робіт і з'ясовують, які завдання їм треба опрацювати вдома (здійснити корекцію).
V. Домашнє завдання
№ 1. За виконаним завданням проведіть аналіз тематичної контрольної роботи.
№ 2. Випереджальне завдання.
- Складіть вираз для обчислення площі S квадрата зі стороною а.
-
За складеним виразом знайдіть S, якщо а = 1; 0,2;
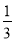 .
.
-
Використовуючи складений вираз, знайдіть а, якщо S = 1;
 ; 0,25.
; 0,25.
- Яких значень можуть набувати змінні S та а у виразі (якщо врахувати, що а та S — довжина сторони квадрата та його площа відповідно).
- За тлумачним словником знайдіть значення слова «залежність».


про публікацію авторської розробки
Додати розробку
