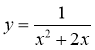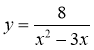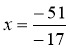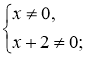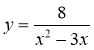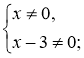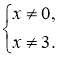Розробка уроку на тему "Функції"

Варіант 1

Варіант 2

1º. Функцію задано формулою

      у = -2х + 7. Визначте:

1º. Функцію задано формулою

      у = 8х – 3. Визначте:

1) значення функції, якщо значення аргументу дорівнює 6;

1) значення функції, якщо значення ар­гументу дорівнює 2;

2) значення аргументу, при якому зна­чення функції дорівнює -9;

2) значення аргументу, при якому зна­чення функції дорівнює -19;

3) чи проходить графік функції через точку А (-4; 15).

3) чи проходить графік функції через точку В (-2; -13)?

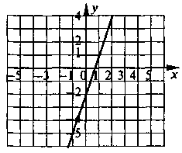
2°. Побудуйте графік функції

     у = 3х – 2. Користуючись графіком, знайдіть:

1) значення функції, що відповідає ар­гументу 2;

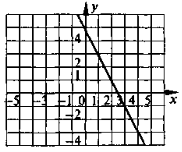
2°. Побудуйте графік функції

     у = -2х + 5. Користуючись графіком, знайдіть:

1) значення функції, що відповідає ар­гументу 2;

2) значення аргументу, при якому зна­чення функції дорівнює -5;

2) значення аргументу, при якому зна­чення функції дорівнює -1;

3) при яких значеннях аргументу функція набуває додатних значень?

3) при яких значеннях аргументу функція набуває від'ємних значень?

3*. Знайдіть координати точок перети­ну графіків функцій у = -38х +15 та  у = -21х – 36.

3*. Знайдіть координати точок перетину графіків функцій

     у = 47х – 9 та у = -13х + 231.

4*. Знайдіть область визначення функції .

4*. Знайдіть область визначення функції .

5*. Не виконуючи побудови, знайдіть координати точок перетину графіка функції у = 0,5х – 3  з осями координат.

5*. Не виконуючи побудови, знайдіть координати точок перетину графіка функції у = -0,8х + 4 з осями координат.

6**. Задайте формулою лінійну функцію, графік якої паралельний до графіка функції у = 3х – 7 і проходить-через точку А(3; 6).

6**. Задайте формулою лінійну функцію, графік якої паралельний до прямої у = -5х + 8 і проходить через точ­ку B(-2; 8).

Варіант 1

Варіант 2

1°. 1) х = 6; у = -2 · 6 + 7 = -5;

2) у = -9; -2х + 7 = -9; -2х = -16; х = 8;

1º. 1) х = 2; у = 8 · 2 – 3 = 13;

2) у = -19; 8х – 3 = -19; 8х = -16; х = -2;

3) А(-4; 15): 15 = -2 · (-4) + 7; 15 = 15 -правильна, отже, графік проходить че­рез т. А.

3) В(-2; -13): -13 = 8 · (-2) – 3 – непра­вильна рівність, отже, т. В не належить графіку.

2°. у = 3х – 2          у > 0, якщо х >.

2° у = -2x + 5          у < 0, якщо х >2,5.

х

0

2

-1

х

0

1

2

3

у

-2

4

-5

у

5

3

1

-1

3*. у = -38х + 15, у = -21х – 36

-38х + 15 = -21х – 36;

-17х = -51; ; х = 3

у = -21 · 3 – 36 = -63 – 36 = -99

А(3; -99)

3*. у = 47х – 9; у = -13х + 231

47х – 9 = -13х + 231;

60х = 240, х = 4

у = 47 · 4 – 9 = 188 – 9 = 179

В(4; 179)

4*.

х² + 2х ≠ 0

х(х + 2) ≠ 0

Область визначення функції х ≠ 0; х ≠ -2.

4*.

х² – 3х ≠ 0

х(х – 3) ≠ 0

Область визначення функції х ≠ 0; х ≠ 3.

5*. у = 0,5х – 3.

Вісь Ох: у = 0; 0,5х – 3 = 0; В(6; 0).

Вісь Оу: х = 0; у = - 3; А(0; - 3).

5*. Вісь Оу: х =0; у = 4; А(0; 4);

вісь Ох: у = 0; -0,8х + 4 = 0; х = 5;

В (5; 0).

6**. Пряма у = 3х – 7 паралельна до

у = kх + b, тому k = 3. Оскільки A(3; 6) належить графіку у = 3х + b,

6**. Пряма у = -5х + 8 і пряма у = kх + b паралельні, тому k = -5.

Оскільки B(-2; 8) належить графіку

то 6 = 3 · 3 + b; b = 6 – 9; b = -3.

Отже, шука­на функція у = 3х - 3

у = -5х + b,

то 8 = -5(-2) + b; b = 8 – 10; b = -2.

Отже, шукана функція у = -5х – 2