Перетворення виразів, що містять корені. Дії над коренями.
Клас: 10-А,Алгебра
Тема уроку: Перетворення виразів, що містять корені. Дії над коренями.
Мета уроку: удосконалити вміння застосовувати властивості арифметичного кореня n-го степеня до перетворення виразів; перевірити поточний рівень знань учнів; розвивати увагу, пам'ять, логічне мислення, розумову діяльність, уміння порівнювати, узагальнювати, проводити аналогію, правильно висловлюватись; виховувати позитивне ставлення до навчання, активність, інтерес до математики.
Тип уроку: урок засвоєння набутих знань.
Обладнання: мультимедійний проектор, комп'ютер,підручник,презентація.
Девіз уроку
Міркуй точно, відповідай чітко, записуй правильно і швидко.
Хід уроку
І. Організаційний етап
Вчитель: Добрий день,шановні діти. Сьогодні наш урок незвичайний, бо у нас багато гостей. Маю надію, що ця зустріч буде успішною, цікавою і вам і нашим гостям. Давайте проведемо цей час з користю і обов’язково з усмішкою. Тож посміхніться! Привітайте один одного посмішкою!
А розпочати сьогоднішній урок я хочу зі слів Евальда Ільєнкова: «Досягнення успішного результату при розв’язуванні задач – не тільки привілей математики. Усе людське життя – це не що інше, як постійна постановка та бажання досягти успіху при розв’язуванні нових питань та проблем».
ІІ. Перевірка домашнього завдання
- Перевірка домашнього завдання за підручником.
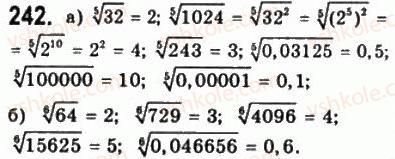
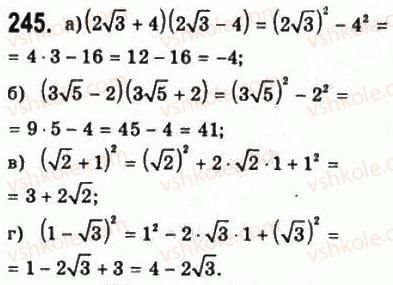
ІІІ. Актуалізація опорних знань
1. Усне опитування учнів.(0,25б)
- Що називають коренем n-го степеня з числа а , де n є N, n> 1?
(Коренем п-го степеня з числа а називається таке число b, п-й степінь якого дорівнює а.)
-
Що називають кубічним коренем із числа а?( Кубічним коренем з числа
 називається число
називається число 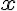 , куб якого дорівнює
, куб якого дорівнює  , тобто
, тобто 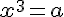 )
)
- Що називають підкореневим виразом?
-
При яких значеннях а має зміст вираз
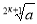 , k є N ?(існує при будь-яких значеннях а)
, k є N ?(існує при будь-яких значеннях а)
- Що називають арифметичним коренем n-го степеня з невід’ємного числа а , де n є N, n> 1?( Арифметичним коренем n-го степеня з числа а називається невід’ємне число, n-й степінь якого дорівнює а.)
-
При яких значеннях а має зміст вираз
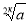 , k є N ?( Значення
, k є N ?( Значення 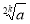 - кореня парного степеня з числа а – існує тільки при
- кореня парного степеня з числа а – існує тільки при 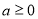 .)
.)
2. Усні вправи (завдання проектуються на дошку, розв’язки з’являються після відповідей учнів)
1. Обчисліть: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
( а) -2; б) 4; в) 1![]() )
)
2. Перетворіть вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
( а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() )
)
3. Повторення формул скороченого множення:
- Розкладіть на множники:
а) х2-16 ; ( (х-4)(х+4) ) б) х-16. ![]()
- Подайте у вигляді квадрата двочлена:
а) а2-6а+9; ![]() б)
б) ![]() .
.![]()
4. Вивчені властивості коренів дають змогу виконувати перетворення коренів. Згадаємо деякі перетворення.
1. Винесення множника з під знака радикала.
В деяких випадках підкореневий вираз розкладається на множники так, що із одного чи декількох із них можна добути точний корінь. Добувши корені із цих множників, одержані числа можна записати перед знаком кореня. Таке перетворення називається винесенням множника за знак радикала.
Наприклад:
![]() ;
;
![]() ;
;
Таким чином, можна зробити висновок: якщо a ![]() 0, b
0, b ![]() 0, то
0, то
![]() .
.
Якщо a — довільне, то ![]() ;
; ![]() .
.
2.Внесення множника під знак радикала.
Перетворення, обернене до винесення множника за знак кореня, називається внесенням множника під знак кореня.
Наприклад:
![]() =
= ![]() =
= ![]() ;
;
3![]() =
= ![]() ·
· ![]() =
= ![]() =
= ![]() ;
;
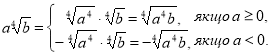
Таким чином, взагалі:
-
Якщо а
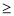 0, b
0, b 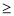 0, то а
0, то а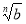 =
= 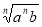 .
.
-
Якщо а — довільне, то
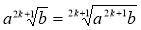 ;
;
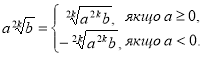
IV. Формування умінь виконувати перетворення коренів
1. Розв’язування вправ відбувається на дошці під керівництвом учителя.
Завдання для учнів
1. Винесення множника з-під знака кореня:
1) ![]() ; 2)
; 2) ![]() .
.
Які властивості квадратного кореня були вами використані?
2. Внесення множника під знак кореня:
1) ![]() ; 2)
; 2) ![]() , якщо
, якщо ![]() ,
, ![]() .
.
3. Порівняти числа:
1) ![]() і
і ![]() ; 2)
; 2) ![]() і
і ![]() .
.
4. Знайти значення виразу:
а) ![]() (Відповідь: -2);
(Відповідь: -2);
б) ![]() (Відповідь: 2).
(Відповідь: 2).
5. Скоротіть дріб : ![]() (Відповідь:
(Відповідь: ![]() ).
).
6. Робота з підручником:
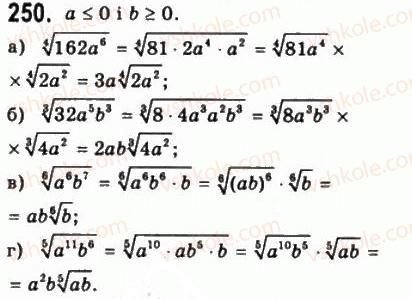
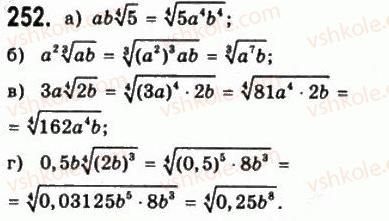
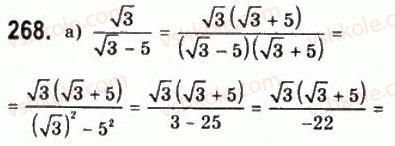

V. Контроль і корекція знань, умінь і навичок
Самостійна робота
|
Варіант 1 |
Варіант 2 |
|
|
Початковий і середній рівні |
||
|
1. Скільки коренів має рівняння
А Жодного Б Один В Два Г Нескінченну множину |
1. Скільки коренів має рівняння
А Два Б Нескінченну множину В Один Г Жодного |
|
|
2. Обчисліть: А 4 Б 8 В 2 Г 128
3. Спростіть вираз
А |
2. Обчисліть: А 16 Б 2 В 1 Г 32
3. Спростіть вираз
А |
|
|
Достатній рівень |
||
|
4. Обчисліть:
|
4. Обчисліть:
|
|
|
Високий рівень |
||
|
5. При яких значеннях змінної
|
5. При яких значеннях змінної
|
|
VI. Підсумок уроку
Учитель відкриває записані на дошці відповіді до самостійної роботи, відповідає на запитання, що виникли.
1.Відповіді до завдань самостійної роботи
|
Завдання |
1 |
2 |
3 |
4 |
5 |
|
Варіант 1 |
А |
В |
В |
1 |
При |
|
Варіант 2 |
В |
Б |
Б |
1 |
При |
2. Рефлексія
1. Що нового ви дізналися сьогодні на уроці?
2. Що нового навчилися?
3. Яким питанням, на вашу думку, потрібно більше приділити уваги вдома?
VII.Домашнє завдання:
1. Завдання за підручником: §6-§7 повторити,№ 289,295
2.Додаткове завдання:
- Спростіть вираз:
а) ![]() ;
;
б) ![]() .
.
-
Спростіть вираз
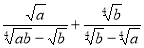 .
.
|
2.Додаткове завдання:
а)
б)
|
|
Картка контролю знань учня |
|||||||
|
10 клас |
|
||||||
(2 бали) |
|
|
|
|
уроці (2 бали) |
Оцінка за урок |
|
|
|
|
|
|
|
|
|
|


про публікацію авторської розробки
Додати розробку
