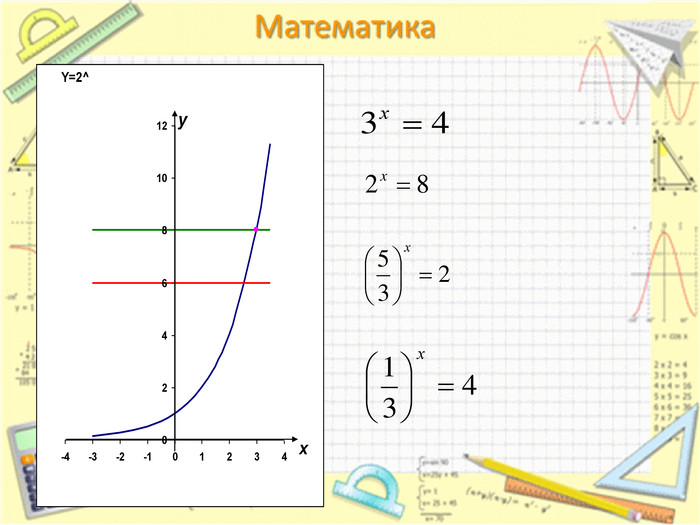
Презентація "Логарифм числа"
Про матеріал
Презентація до уроку на тему: "Логарифм числа" для учнів 11 класу профільного рівня навчання Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку