Урок "Перпендикуляр і похила в просторі"

Про матеріал

Мета уроку:

• формувати ключові компетентності та вміння для роботи з перпендикуляром, похилою, поняттям відстані у просторі;

• формувати процедурну, дослідницьку компетентності;

• розвивати комунікативну компетентність;

• створення умов для самостійного пошуку;

• показати роль та можливості математики у пізнанні та описанні реальних процесів і явищ.

Обладнання: стереометричний набір.

Перегляд файлу

Перпендикуляр і похила в просторі.

Мета уроку:

формувати ключові компетентності та вміння для роботи з перпендикуляром, похилою, поняттям відстані у просторі;
формувати процедурну, дослідницьку компетентності;
розвивати комунікативну компетентність;
створення умов для самостійного пошуку;
показати роль та можливості математики у пізнанні та описанні реальних процесів і явищ.

Обладнання: стереометричний набір.

Хід уроку

І. Налаштування на успішну роботу (попросити учнів сісти рівно, а потім покласти одну долоню на лоба, іншу – на потилицю. Потім треба заплющити очі, сконцентруватися на майбутньому занятті та зробити кілька глибоких вдихів-видихів.)

IІ. Перевірка домашнього завдання.

Виправити помилки, допущені в записах при розв’язуванні задач домашньої роботи.

ІIІ. Актуалізація опорних знань

1) Дано площину α, перпендикулярну до неї пряму а і іншу пряму b, яка не лежить в площині α. Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) якщо b || a, то b α; +

в) якщо b α, то а і b мимобіжні; -

б) якщо b α , то b || а ; +

г) якщо b α, то а і b перетинаються. -

2) Точка S лежить поза площиною ромба АВСD, причому SВ⊥ВС, SВ⊥АВ, ∠ВАD = 60°. Які з наведених тверджень правильні, а які – неправильні:

а) пряма SВ перпендикулярна до площини АВС; +

б) пряма АВ перпендикулярна до площини SВС; -

в) пряма ВС перпендикулярна до площини АSВ; -

г) пряма SВ перпендикулярна до прямої ВD? +

А якщо в умові змінити ромб на квадрат, що можна сказати про всі ці твердження?

3) Розв’язати усно задачі на перпендикуляр і похилу до прямої.

ІV. Мотивація навчальної діяльності

Ми згадали поняття перпендикуляра, похилої та її проекції до прямої на площині. В оточуючому нас просторі ви, безперечно мали змогу спостерігати наочні приклади перпендикулярів та похилих до площини земної поверхні, підлоги в приміщеннях. Наведіть приклади. (Прикладами є кріплення телевізійних вишок, антен, штативи для фотокамер)

А тому на практиці потрібно вміти щось виміряти, а щось і обчислити із таких елементів як довжини перпендикуляра, похилих та їх проекцій, а також знаючи їх властивості, створювати відповідні математичні моделі для розв’язування задач. Тому сьогодні ми працюємо над темою “Перпендикуляр і похила у просторі”. Розуміти та вміти застосовувати даний матеріал необхідно тому, що (відповіді учнів – встановити ялинку, виготовити цікаву підставку для квітів, побудувати опори для мосту)

Щоб виміряти глибину річки геодезисти опускають у річку грузило, до якого прив’язані два шнури довжиною m і n з гумовими кулями. Коли грузило опуститься на дно, кулі під дією течії відпливуть на певну відстань і зупиняться в точках А і В. Сфотографувавши їх і вимірявши на знімку відстань між кулями, геодезисти і обчислюють глибину h річки. А як саме? (Змоделювати ситуацію в зошитах)

V. Дослідження властивостей перпендикуляра, похилих та їх проекцій.

За допомогою стереометричних моделей дослідити:

довжину перпендикуляра і похилої, проведених до площини з точки поза нею;
кількість перпендикулярів і похилих, проведених до площини з точки поза нею;
порівняти довжини похилих та їх проекцій, якщо похилі проведені до площини з однієї точки мають однакову довжину; різні довжини;
що спільного та чим відрізняються властивості перпендикуляра, похилих та їх проекцій в планіметрії і стереометрії;
зробити висновки.

VI. Формування умінь і навичок

Усне розв’язування задач (за підручником А. Г. Мерзляк …)

№35.1 - 1) ДС; 2) С; 3) А

№35.2 - 1); 2) Д; 3)Д.

Письмове розв’язування задач

№35.5 - АС=4см, СД= (см).

Кінезеологічна вправа. Для зняття напруження, притоку крові до головного мозку, для поліпшення уваги виконуємо наступні рухи

праву руку покласти на лівий м’яз між шиєю та плечем;
стиснути м’яз та поволі повертати голову зліва направо;
потім почати рух в зворотній бік;
губи скласти трубочкою і на видиху вимовити «ух!»;
поміняти руку, поклавши її на правий м’яз та повторити вправу.

Із точки S проведено до площини 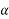перпендикуляр SO та похилі SA і SB. Довжини похилих відповідно дорівнюють 13 і 20 см. Довжина проекції похилої AS дорівнює 5 см (рис. 164). Знайти відстань від точки S до площини та довжину проекції похилої SB.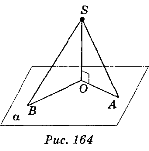

Відповідь: SO=12 см; BO=16 см.

2. З вершини A квадрата АВСD проведено перпендикуляр KA до його площини. Знайдіть відстань CK, якщо KA дорівнює 6 см, а сторона квадрата - 4 см.

Розв’язання.

Проведемо діагональ АС квадрата АВСD. ∆АСK – прямокутний, оскільки KAАС за означенням перпендикулярності прямої і площини.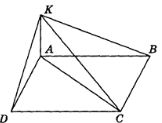

АС = АD = 4∙∙ = 8( см).

З ∆АСK : CK = (см)

Відповідь: CK=10 см.

Робота з підручником (ст. 187) - поняття відстані від точки до площини

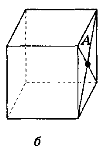
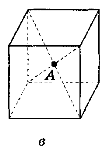
3. Знайти відстань від точки А до граней куба, якщо ребро куба дорівнює 10 см

VII. Підведення підсумків

Порівняти довжини похилих на готових рисунках (в презентації).

Проаналізувати урок з точки зору учнів (письмово або усно)

Плюс – мінус - цікаво

+ що сподобалось на уроці, що здалося цікавим та корисним

- що не сподобалось, здалося важким, незрозумілим та нудним.

Ц факти, про які дізнались на уроці, про що ще б хотілось дізнатися.

VIII. Домашнє завдання

Опрацювати п.35, №35.4, №35.6, №35.13.

Роздатковий матеріал

За допомогою стереометричних моделей дослідити:

1)довжину перпендикуляра і похилої, проведених до площини з точки поза нею;

2) кількість перпендикулярів і похилих, проведених до площини з точки поза нею;

3)порівняти довжини похилих та їх проекцій, якщо похилі проведені до площини з однієї точки мають однакову довжину; різні довжини;

4) що спільного та чим відрізняються властивості перпендикуляра, похилих та їх проекцій в планіметрії і стереометрії; 5)зробити висновки.

Задача 1. Із точки S проведено до площини перпендикуляр SO та похилі SA і SB. Довжини похилих відповідно дорівнюють 13 і 20 см. Довжина проекції похилої AS дорівнює 5 см (рис. 164). Знайти відстань від точки S до площини та довжину проекції похилої SB.

Задача 2. З вершини A квадрата АВСD проведено перпендикуляр KA до його площини. Знайдіть відстань CK, якщо KA дорівнює 6 см, а сторона квадрата - 4 см.